1s complement 1 n 1s complement nbits q

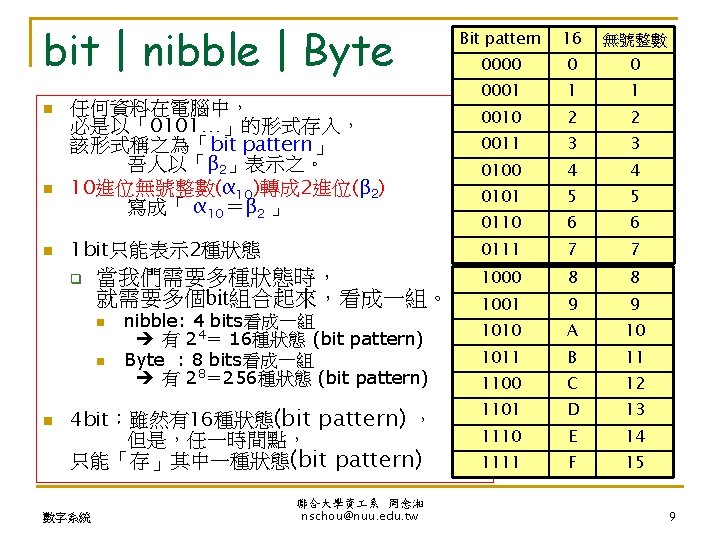
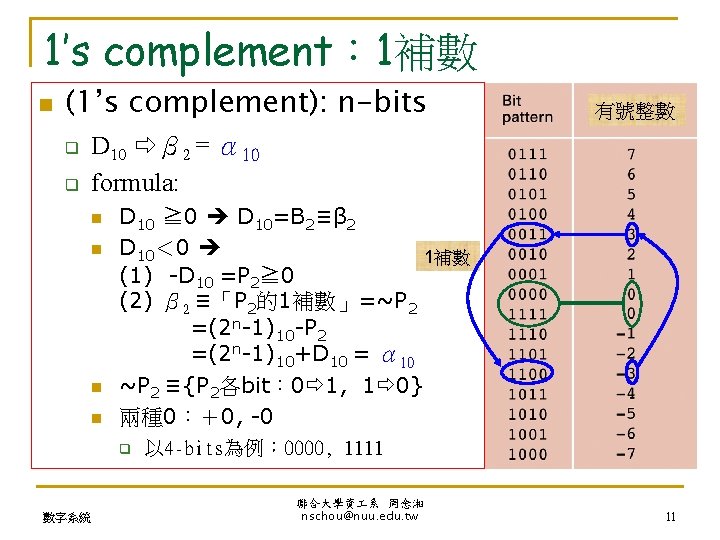
1’s complement： 1補數 n (1’s complement): n-bits q q 有號整數 D 10 β 2 = α 10 formula: n n D 10 ≧ 0 D 10=B 2≡β 2 D 10＜ 0 1補數 (1) -D 10 =P 2≧ 0 (2) β 2 ≡「P 2的1補數」=~P 2 =(2 n-1)10 -P 2 =(2 n-1)10+D 10 = α 10 ~P 2 ≡{P 2各bit： 0 1, 1 0} 兩種 0：＋0, -0 q 數字系統 以 4 -bits為例： 0000, 1111 聯合大學資 系 周念湘 nschou@nuu. edu. tw 11

2’s complement： 2補數 n (1’s complement)+1 q q D 10 β 2 = α 10 formula: n n n D 10≧ 0 D 10=B 2=β 2 MSB=0 2補數 D 10 ＜ 0 //D 10=-410 (1) -D 10 = P 2 //P 2=410=01002 (2) β 2 = P 2的2補數(11002)=~P 2+1 =(2 n-1)10 -P 2+1 =(2 n)10+D 10 = α 10 12 MSB=1 X-Y=X+(-Y) -Y=Y的2補數 數字系統 聯合大學資 系 周念湘 nschou@nuu. edu. tw 12

2’s complement： 2補數 n D 10＜ 0 q q 「令S’ 2 =D’ 10 」 D 10 β 2≡(1 S’)2=α 10=2 n+D 10 =2 n-1+ S’ 2=2 n-1+D’ 10 D 10 = 2 n-1+ D’ 10 -2 n = D’ 10 -2 n-1 舉例： n n n 數字系統 D 10=-6 10102=1010=23+0102 S’ 2 =0102=210=D’ 10 D 10=-6=210 -23=D’ 10 -24 -1 聯合大學資 系 周念湘 nschou@nuu. edu. tw 13

(A+B)2： illegal : cn⊕cn-1=1 n n n C=cncn-1 cn-2 cn-3…c 0 A= an-1 an-2 an-3…a 0 B= bn-1 bn-2 bn-3…b 0 -2 n-1≦ A+B=Z < 2 n-1 (cn=0)⊕(cn-1=1)=1 overflow q q q 數字系統 cn=0, cn-1=1 an-1=bn-1=0 C=01 cn-2 cn-3…c 0 A= 0 an-2 an-3…a 0 >0 B= 0 bn-2 bn-3…b 0 >0 (+ ---------------Z= 1 zn-2 zn-3…z 0 <0 (正＋正變負) cn-1=1 A+B≧ 2 n-1 →← overflow 聯合大學資 系 周念湘 nschou@nuu. edu. tw 14

(A+B)2： illegal : cn⊕cn-1=1 n n n C=cncn-1 cn-2 cn-3…c 0 A= an-1 an-2 an-3…a 0 B= bn-1 bn-2 bn-3…b 0 -2 n-1≦ A+B=Z < 2 n-1 (cn=1)⊕(cn-1=0)=1 underflow q q q 數字系統 cn=1, cn-1=0 an-1=bn-1=1 (A, B<0) C=10 cn-2 cn-3…c 0 A= 1 an-2 an-3…a 0 <0 令A=1 A’ B= 1 bn-2 bn-3…b 0 <0 (+ 令 B=1 B’ ---------------Z= 0 zn-2 zn-3…z 0 ≧ 0 (負＋負變正) cn-1=0 0≦A’+B’<2 n-1 (Z>0) A+B=(A’- 2 n-1)+(B’- 2 n-1) =A’+B’- 2 n <2 n-1 -2 n <-2 n-1 →← underflow 聯合大學資 系 周念湘 nschou@nuu. edu. tw 15

(A+B)2： legal : cn⊕cn-1=0 n n n C=cncn-1 cn-2 cn-3…c 0 A= an-1 an-2 an-3…a 0 B= bn-1 bn-2 bn-3…b 0 -2 n-1≦ A+B < 2 n-1 cn⊕cn-1=0 q cn=1, cn-1=1 drop cn n q cn=0, cn-1=0 do nothing n q 試證明 A＊B<0 則 A＋B<0 A+B<0 (MSB=1) n 數字系統 試證明 A＊B<0 則 A＋B>0 轉成 10進位時， 結果需再取 2補數，前面加上負號。 聯合大學資 系 周念湘 nschou@nuu. edu. tw 16

(A/B)2： 「left shift」「-」 n n n 11002/1012 R 1 = 11002 -(101)2*25 Q 1=1*25 = 1011002 R 2 = 1011002 -(101)2*23 Q 2=1*23 = 1002 Ans: Q=Q 1+Q 2=1000002+10002=1010002 =4010 R=R 2 = 1002 = 410 驗證：(1100)2 /1012=20410/510=40餘 4 減法會用「加 2補數」做 數字系統 聯合大學資 系 周念湘 nschou@nuu. edu. tw 18

Excess 2 n-1 表示法 2’s complement Excess-8 15 n excess-8 q D 10 β 2 = α 10 = n q q 14 (23) 13 (D+2 n-1) 12 10 D 10=6 β 2 =11102 = 1410 =(6+8)10 是 2 n-1 -D D 10≧ 0 β 2 10的2補數 D 10＜ 0 β 2 是 2 n-1+D 10的2進位 11 10 9 8 7 6 5 4 3 q 數字系統 β 2 = α 10 α 10 - 2 n 2 2 n-1 if α 10 <2 n-1 otherwise 聯合大學資 系 周念湘 nschou@nuu. edu. tw 1 0 19

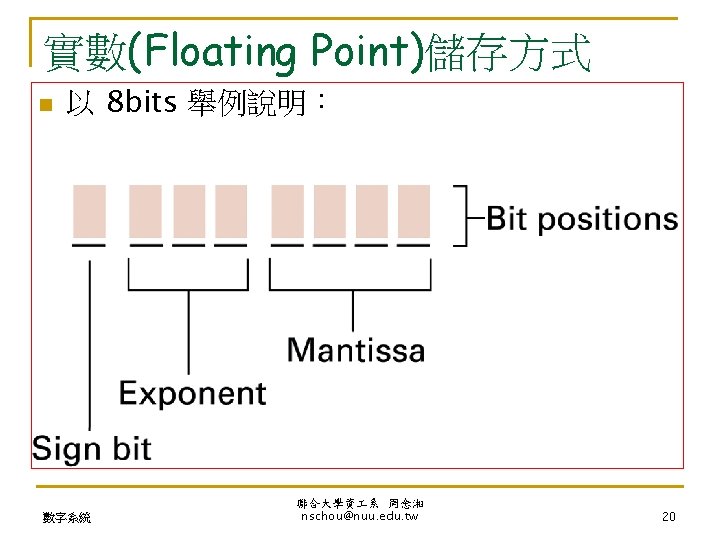
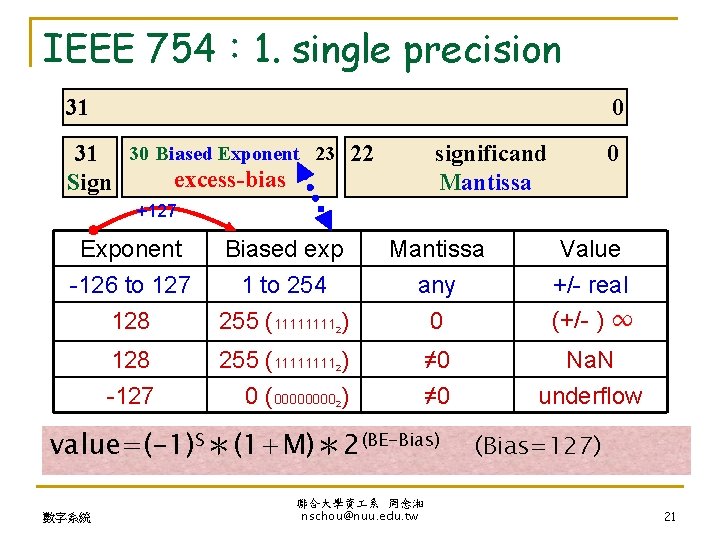
IEEE 754： 1. single precision 31 0 31 30 Biased Exponent 23 22 excess-bias Sign significand Mantissa 0 +127 Exponent -126 to 127 128 Biased exp 1 to 254 255 (1111 ) Mantissa any 0 Value +/- real (+/- ) ∞ 128 -127 255 (1111 ) 0 (0000 ) ≠ 0 Na. N underflow 2 2 2 value=(-1)S＊(1+M)＊2(BE-Bias) 數字系統 聯合大學資 系 周念湘 nschou@nuu. edu. tw (Bias=127) 21

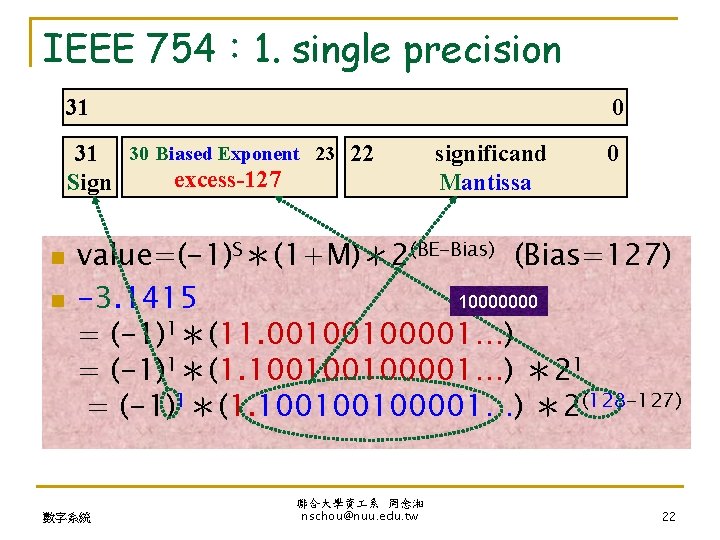
IEEE 754： 1. single precision 31 0 31 30 Biased Exponent 23 22 excess-127 Sign n n significand Mantissa 0 value=(-1)S＊(1+M)＊2(BE-Bias) (Bias=127) 10000000 -3. 1415 = (-1)1＊(11. 00100100001…) = (-1)1＊(1. 100100100001…) ＊21 = (-1)1＊(1. 100100100001…) ＊2(128 -127) 數字系統 聯合大學資 系 周念湘 nschou@nuu. edu. tw 22

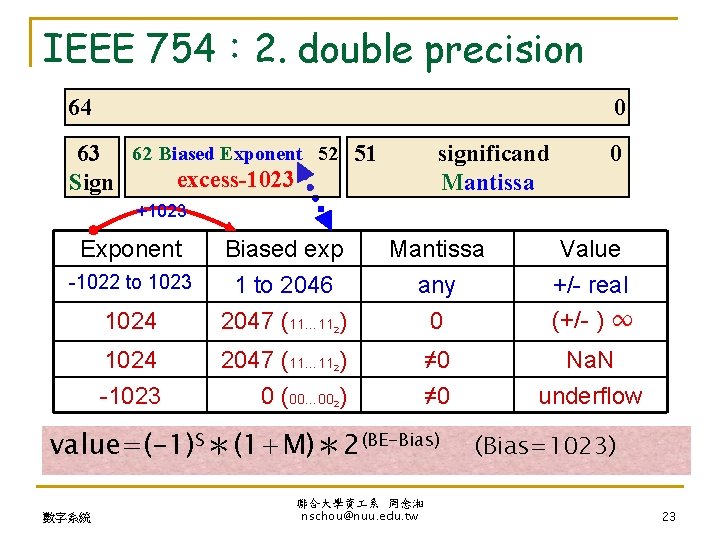
IEEE 754： 2. double precision 64 0 63 62 Biased Exponent 52 51 excess-1023 Sign significand Mantissa 0 +1023 Exponent 1024 Biased exp 1 to 2046 2047 (11… 11 ) Mantissa any 0 Value +/- real (+/- ) ∞ 1024 -1023 2047 (11… 11 ) 0 (00… 00 ) ≠ 0 Na. N underflow -1022 to 1023 2 2 2 value=(-1)S＊(1+M)＊2(BE-Bias) 數字系統 聯合大學資 系 周念湘 nschou@nuu. edu. tw (Bias=1023) 23

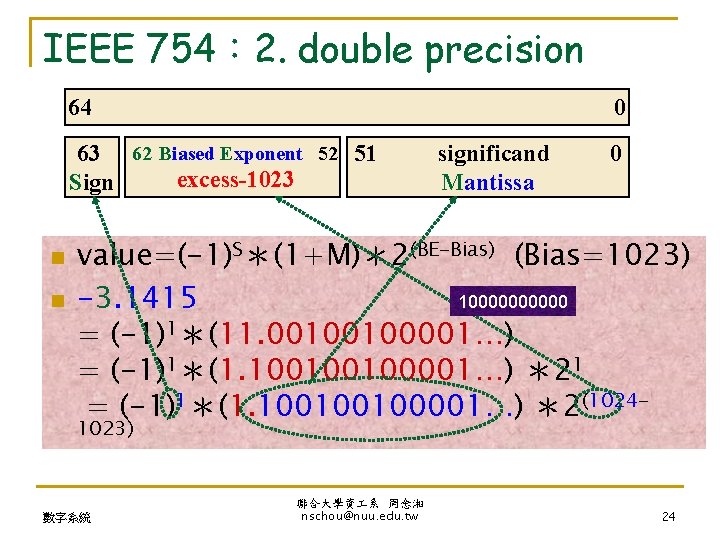
IEEE 754： 2. double precision 64 0 63 62 Biased Exponent 52 51 excess-1023 Sign n n significand Mantissa 0 value=(-1)S＊(1+M)＊2(BE-Bias) (Bias=1023) 100000 -3. 1415 = (-1)1＊(11. 00100100001…) = (-1)1＊(1. 100100100001…) ＊21 = (-1)1＊(1. 100100100001…) ＊2(10241023) 數字系統 聯合大學資 系 周念湘 nschou@nuu. edu. tw 24