19 Principal Stresses I Main Topics A Cauchys

19. Principal Stresses I Main Topics A Cauchy’s formula B Principal stresses (eigenvectors and eigenvalues) C Example 11/26/2020 GG 303 1

19. Principal Stresses http: //hvo. wr. usgs. gov/kilauea/update/images. html 11/26/2020 GG 303 2

19. Principal Stresses II Cauchy’s formula A Relates traction (stress vector) components to stress tensor components in the same reference frame B 2 D and 3 D treatments analogous C τi = σij nj = njσij 11/26/2020 GG 303 Note: all stress components shown are positive 3

19. Principal Stresses II Cauchy’s formula (cont. ) C τi = njσji 1 Meaning of terms a τi = traction component b nj = direction cosine of angle between ndirection and jdirection c σji = traction component d τi and σji act in the same direction 11/26/2020 GG 303 nj = cosθnj = anj 4

19. Principal Stresses II Cauchy’s formula (cont. ) D Expansion (2 D) of τi = nj σji 1 τx = nx σxx + ny σyx 2 τy = nx σxy + ny σyy nj = cosθnj = anj 11/26/2020 GG 303 5

19. Principal Stresses II Cauchy’s formula (cont. ) E Derivation: Note that all contributions must act in x-direction Contributions to τx 1 2 nx = cosθnx = anx ny = cosθny = any 3 11/26/2020 GG 303 6

19. Principal Stresses II Cauchy’s formula (cont. ) E Derivation: Note that all contributions must act in y-direction Contributions to τy 1 2 nx = cosθnx = anx ny = cosθny = any 3 11/26/2020 GG 303 7

19. Principal Stresses II Cauchy’s formula (cont. ) F Alternative forms 1 τi = njσji 2 τi = σjinj 3 τi = σijnj 4 5 Matlab a t = s’*n b t = s*n 11/26/2020 3 D nj = cosθnj = anj GG 303 8

19. Principal Stresses III Principal stresses (eigenvectors and eigenvalues) Cauchy’s Formula A B Vector components C The form of (C ) is [A][X=λ[X], and [σ] is symmetric 11/26/2020 GG 303 9

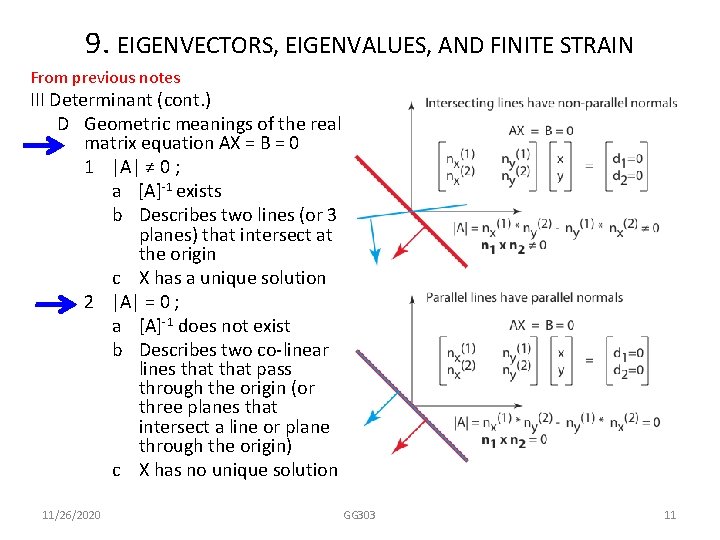
9. EIGENVECTORS, EIGENVALUES, AND From previous notes FINITE STRAIN III Eigenvalue problems, eigenvectors and eigenvalues (cont. ) E Alternative form of an eigenvalue equation 1 [A][X]=λ[X] Subtracting λ[IX] = λ[X] from both sides yields: 2 [A-Iλ][X]=0 (same form as [A][X]=0) F Solution conditions and connections with determinants 1 Unique trivial solution of [X] = 0 if and only if |A-Iλ|= 0 2 Eigenvector solutions ([X] ≠ 0) if and only if |A-Iλ|=0 11/26/2020 GG 303 10

9. EIGENVECTORS, EIGENVALUES, AND FINITE STRAIN From previous notes III Determinant (cont. ) D Geometric meanings of the real matrix equation AX = B = 0 1 |A| ≠ 0 ; a [A]-1 exists b Describes two lines (or 3 planes) that intersect at the origin c X has a unique solution 2 |A| = 0 ; a [A]-1 does not exist b Describes two co-linear lines that pass through the origin (or three planes that intersect a line or plane through the origin) c X has no unique solution 11/26/2020 GG 303 11

9. EIGENVECTORS, EIGENVALUES, AND FINITE STRAIN From previous notes III Eigenvalue problems, eigenvectors and eigenvalues (cont. ) J Characteristic equation: |A-Iλ|=0 3 Eigenvalues of a symmetric 2 x 2 matrix a b Radical term cannot be negative. Eigenvalues are real. c d 11/26/2020 GG 303 12

9. EIGENVECTORS, EIGENVALUES, AND From previous notes FINITE STRAIN L Distinct eigenvectors (X 1, X 2) of a symmetric 2 x 2 matrix are perpendicular Since the left sides of (2 a) and (2 b) are equal, the right sides must be equal too. Hence, 4 λ 1 (X 2 • X 1) =λ 2 (X 1 • X 2) Now subtract the right side of (4) from the left 5 (λ 1 – λ 2)(X 2 • X 1) =0 • The eigenvalues generally are different, so λ 1 – λ 2 ≠ 0. • This means for (5) to hold that X 2 • X 1 =0. • Therefore, the eigenvectors (X 1, X 2) of a symmetric 2 x 2 matrix are perpendicular 11/26/2020 GG 303 13

19. Principal Stresses III Principal stresses (eigenvectors and eigenvalues) D Meaning 1 Since the stress tensor is symmetric, a reference frame with perpendicular axes defined by nx and ny pairs can be found such that the shear stresses are zero 2 This is the only way to satisfy the equation above; otherwise σxy ny ≠ 0, and σxy nx ≠ 0 3 For different (principal) values of λ, the orientation of the corresponding principal axis is expected to differ 11/26/2020 GG 303 14

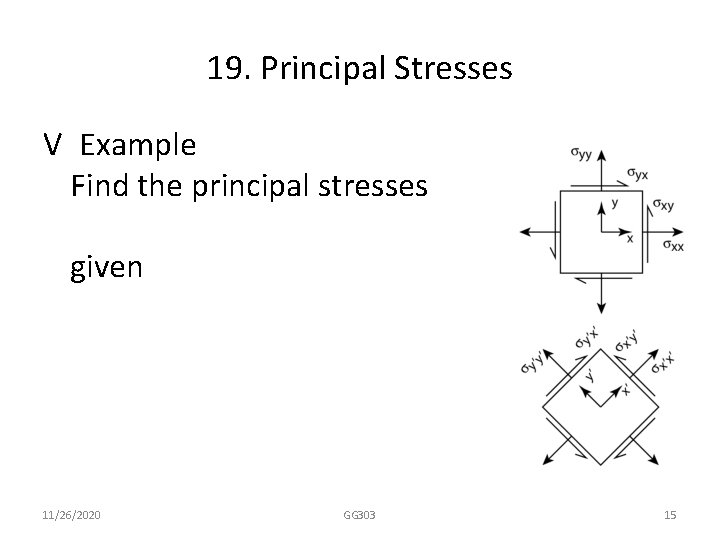
19. Principal Stresses V Example Find the principal stresses given 11/26/2020 GG 303 15

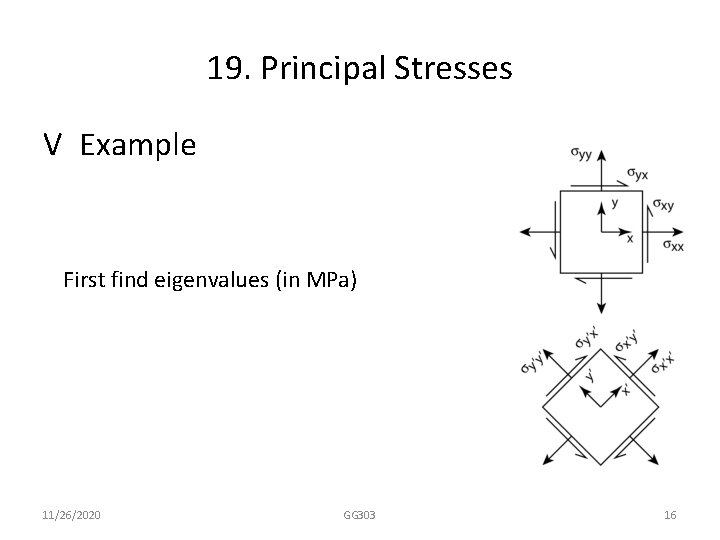
19. Principal Stresses V Example First find eigenvalues (in MPa) 11/26/2020 GG 303 16

19. Principal Stresses IV Example Eigenvalues (MPa) Then solve for eigenvectors (X) using [A-Iλ][X]=0 11/26/2020 GG 303 17

19. Principal Stresses IV Example Eigenvalues Eigenvectors y y x x Note that X 1 • X 2 = 0 Principal directions are perpendicular 11/26/2020 GG 303 18

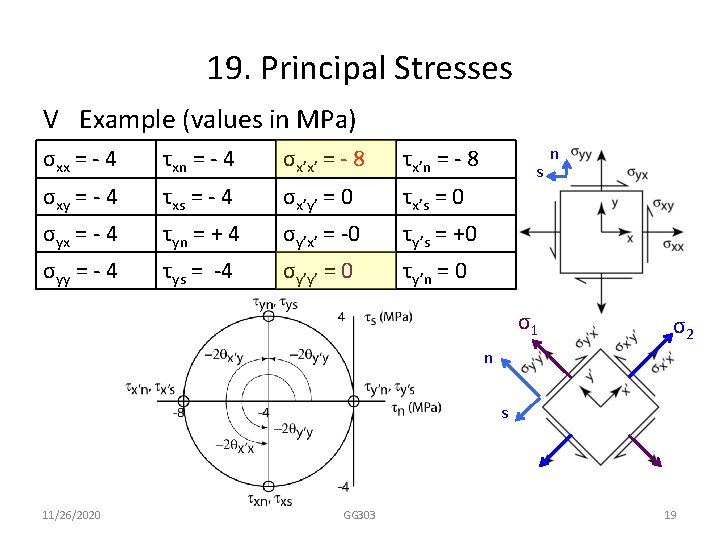
19. Principal Stresses V Example (values in MPa) σxx = - 4 τxn = - 4 σx’x’ = - 8 τx’n = - 8 σxy = - 4 τxs = - 4 σx’y’ = 0 τx’s = 0 σyx = - 4 τyn = + 4 σy’x’ = -0 τy’s = +0 σyy = - 4 τys = -4 σy’y’ = 0 τy’n = 0 s σ1 n σ2 n s 11/26/2020 GG 303 19

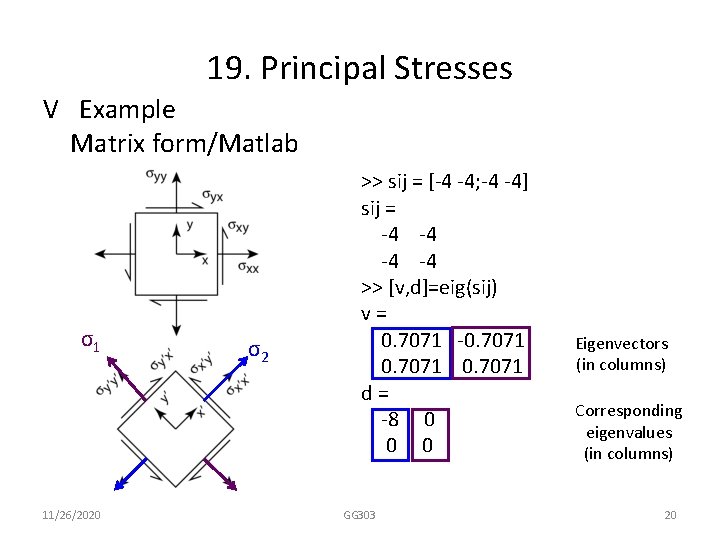
19. Principal Stresses V Example Matrix form/Matlab σ1 11/26/2020 σ2 >> sij = [-4 -4; -4 -4] sij = -4 -4 >> [v, d]=eig(sij) v= 0. 7071 -0. 7071 d= -8 0 0 0 GG 303 Eigenvectors (in columns) Corresponding eigenvalues (in columns) 20