18 Heat Work First Law of Thermodynamics 1

18. Heat, Work, & First Law of Thermodynamics 1. 2. 3. The 1 st Law of Thermodynamics Thermodynamic Processes Specific Heats of an Ideal Gas

A jet aircraft engine converts the energy of burning fuel into mechanical energy. How does energy conservation apply in this process? E combustion = E mech + Q waste

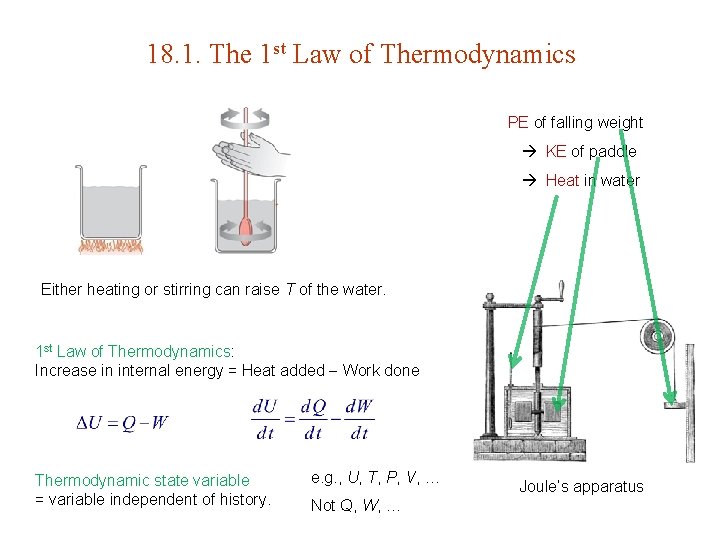
18. 1. The 1 st Law of Thermodynamics PE of falling weight KE of paddle Heat in water Either heating or stirring can raise T of the water. 1 st Law of Thermodynamics: Increase in internal energy = Heat added Work done Thermodynamic state variable = variable independent of history. e. g. , U, T, P, V, … Not Q, W, … Joule’s apparatus

Example 18. 1. Thermal Pollution The reactor in a nuclear power plant supplied energy at the rate of 3. 0 GW, boiling water to produce steam that turns a turbine-generator. The spent steam is then condensed through thermal contact with water taken from a river. If the power plant produces electrical energy at the rate of 1. 0 GW, at what rate is heat transferred to the river? 1 st law From standpoint of power plant: ( loses heat to river )

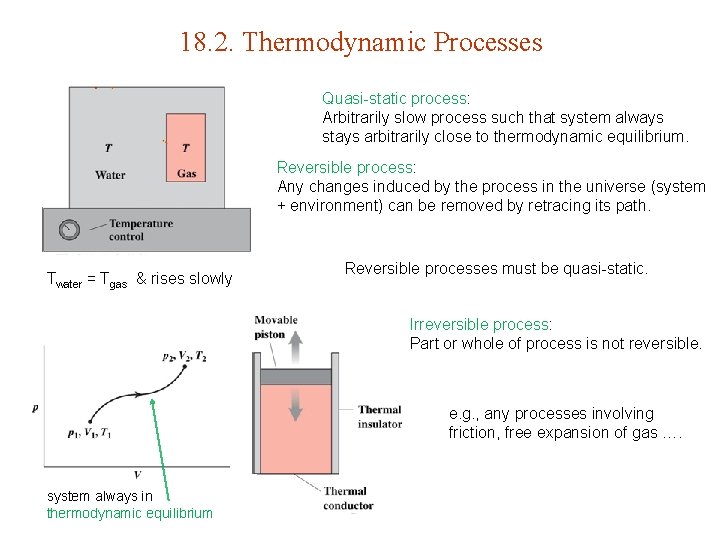
18. 2. Thermodynamic Processes Quasi-static process: Arbitrarily slow process such that system always stays arbitrarily close to thermodynamic equilibrium. Reversible process: Any changes induced by the process in the universe (system + environment) can be removed by retracing its path. Twater = Tgas & rises slowly Reversible processes must be quasi-static. Irreversible process: Part or whole of process is not reversible. e. g. , any processes involving friction, free expansion of gas …. system always in thermodynamic equilibrium

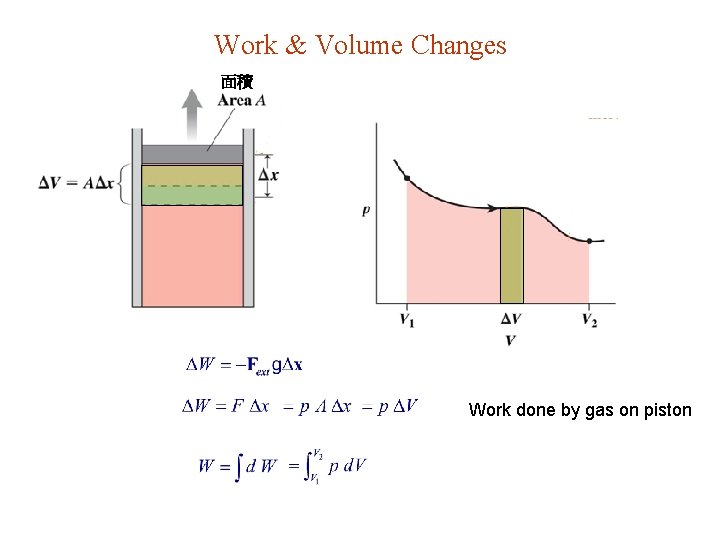
Work & Volume Changes 面積 Work done by gas on piston

GOT IT? 18. 1. Two identical gas-cylinder systems are taken from the same initial state to the same final state, but by different processes. Which are the same in both cases: (a) the work done on or by the gas, (b) the heat added or removed, or (c) the change in internal energy?

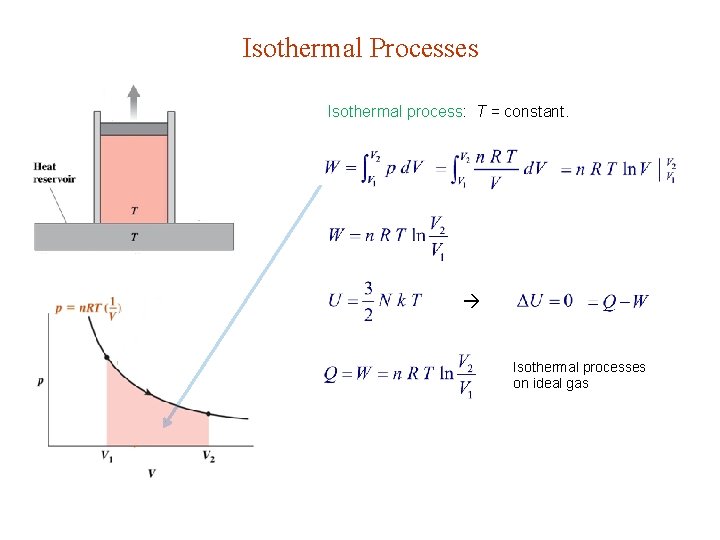
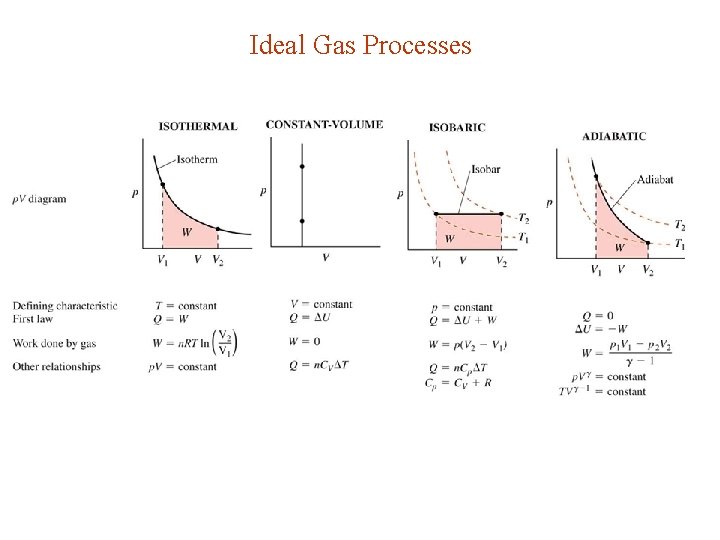
Isothermal Processes Isothermal process: T = constant. Isothermal processes on ideal gas

Example 18. 2. Bubbles! A scuba diver is 25 m down, where the pressure is 3. 5 atm ( 350 k. Pa ). The air she exhales forms bubbles 8. 0 mm in radius. How much work does each bubble do as it arises to the surface, assuming the bubbles remain at 300 K. T = const

Constant-Volume Processes & Specific Heat Constant-volume process ( isometric, isochoric, isovolumic ) : V = constant CV = molar specific heat at constant volume isometric processes Ideal gas: U = U(T) Non-ideal gas: for all processes only for isometric processes

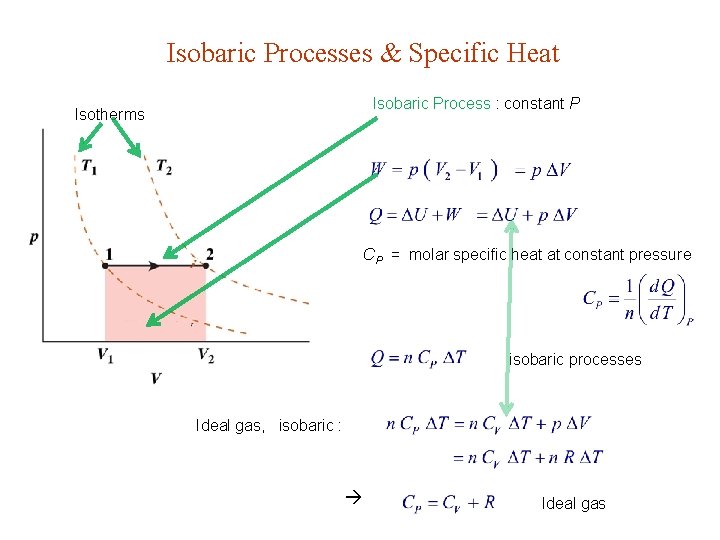
Isobaric Processes & Specific Heat Isobaric Process : constant P Isotherms CP = molar specific heat at constant pressure isobaric processes Ideal gas, isobaric : Ideal gas

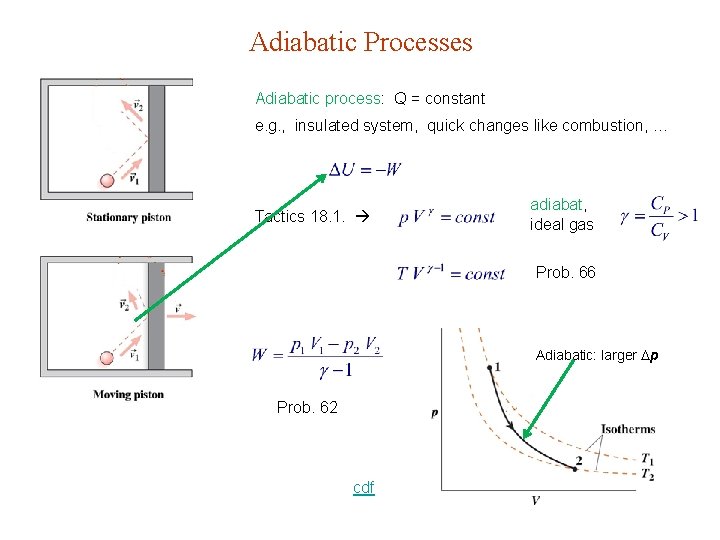
Adiabatic Processes Adiabatic process: Q = constant e. g. , insulated system, quick changes like combustion, … Tactics 18. 1. adiabat, ideal gas Prob. 66 Adiabatic: larger p Prob. 62 cdf

TACTIC 18. 1. Adiabatic Equation Ideal gas, any process: Adiabatic process:

Conceptual Example 18. 1. Ideal-Gas Law vs Adiabatic Equation The ideal gas law says p V = n R T, but the adiabatic equation says p V = const. Which is right ? Both are right. The adiabatic equation is a special case where T V +1

Making the Connection Suppose you halve the volume of an ideal gas with = 1. 4. What happens to the pressure if the process is (a) isothermal and (b) adiabatic? Ans: (a) p. V = const p = 2 p 0 (doubles) (b) p V = const p = p 0 2 = 2. 64 p 0

Example 18. 3. Diesel Power Fuel ignites in a diesel engine from the heat of compression (no spark plug needed). Compression is fast enough to be adiabatic. If the ignit temperature is 500 C, what compression ratio Vmax / Vmin is needed? Air’s specific heat ratio is = 1. 4, & before the compression the air is at 20 C.

Application: Smog Alert! Air is poor heat conductor convection is adiabatic. If rising air cools slower than surrounding air, pollution rises high & can be dispersed. Otherwise, smog.

GOT IT? 18. 2. Name the basic thermodynamic process involved when each of the following is done to a piston-cylinder system containing ideal gas, & tell also whether T, p, V, & U increase or decrease. (a) the piston is lock in place& a flame is applied to the bottom of the cylinder, (b) the cylinder is completely insulated & the piston is pushed downward, (c) the piston is exposed to atmospheric pressure & is free to move, while the cylinder is cooled by placing it on a block of ice. (a) isometric; T , p , V =const, U . (b) adiabatic; T , p , V , U . (c) isobaric; T , p =const, V , U .

Ideal Gas Processes

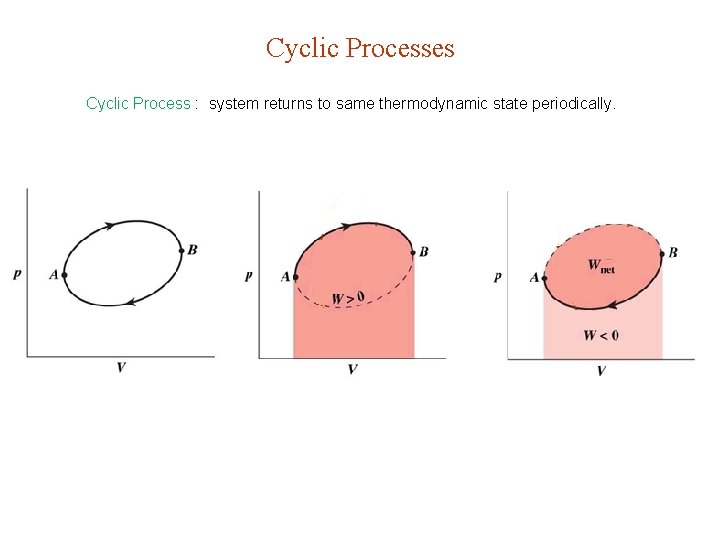
Cyclic Processes Cyclic Process : system returns to same thermodynamic state periodically.

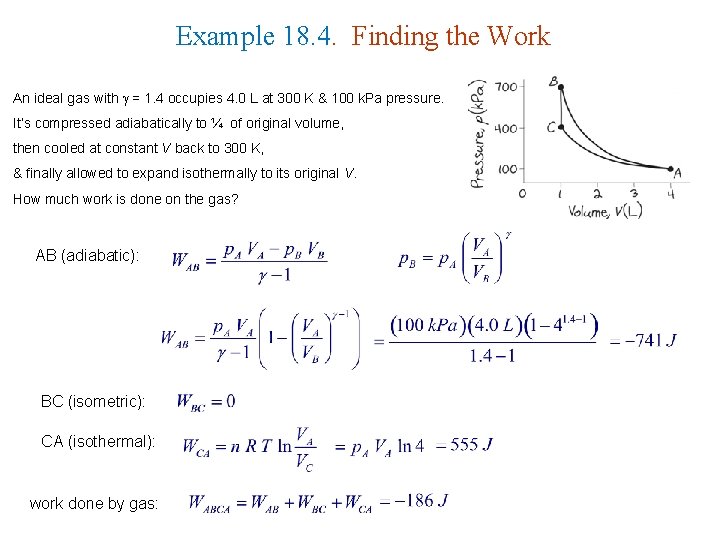
Example 18. 4. Finding the Work An ideal gas with = 1. 4 occupies 4. 0 L at 300 K & 100 k. Pa pressure. It’s compressed adiabatically to ¼ of original volume, then cooled at constant V back to 300 K, & finally allowed to expand isothermally to its original V. How much work is done on the gas? AB (adiabatic): BC (isometric): CA (isothermal): work done by gas:

18. 3. Specific Heats of an Ideal Gas Ideal gas: Experimental values ( room T ): For monatomic gases, 5/3, e. g. , He, Ne, Ar, …. For diatomic gases, 7/5 = 1. 4, CV = 5 R/2, e. g. , H 2 , O 2 , N 2 , …. For tri-atomic gases, 1. 3, CV = 3. 4 R, e. g. , SO 2 , NO 2 , …. Degrees of freedom (Do. F) = number of independent coordinates required to describe the system Single atom: Do. F = 3 (transl) For low T ( vib modes not active ) : Rigid diatomic molecule : Do. F = 5 (3 transl + 2 rot) Rigid triatomic molecule : Do. F = 6 (3 transl + 3 rot)

The Equipartition Theorem Equipartition theorem ( kinetic energy version): For a system in thermodynamic equilibrium, each degree of freedom of a rigid molecule contributes ½ k. T to its average energy. Equipartition theorem ( general version): For a system in thermodynamic equilibrium, each degree of freedom described by a quadratic term in the energy contributes ½ k. T to its average energy. Do. F ( f ) CV CP Monatomic 3 3/2 5/3 Diatomic 5 5/2 7/5 Triatomic 6 3 4 4/3

Example 18. 5. Gas Mixture A gas mixture consists of 2. 0 mol of oxygen (O 2) & 1. 0 mol of Argon (Ar). Find the volume specific heat of the mixture.

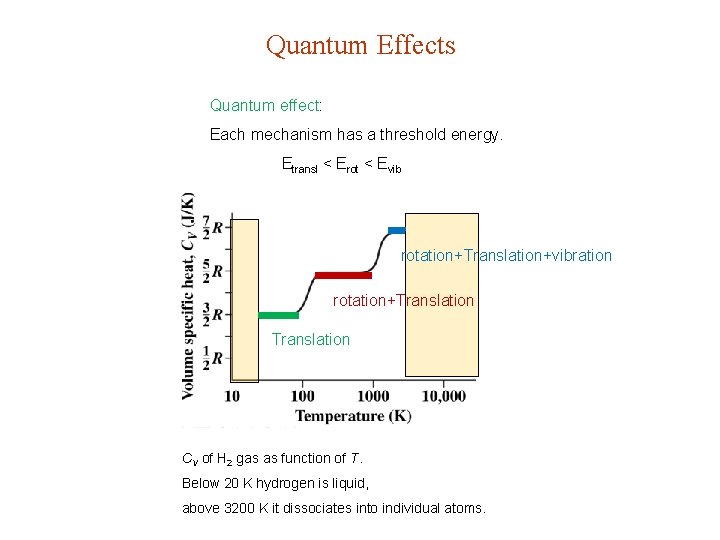
Quantum Effects Quantum effect: Each mechanism has a threshold energy. Etransl < Erot < Evib rotation+Translation+vibration rotation+Translation CV of H 2 gas as function of T. Below 20 K hydrogen is liquid, above 3200 K it dissociates into individual atoms.

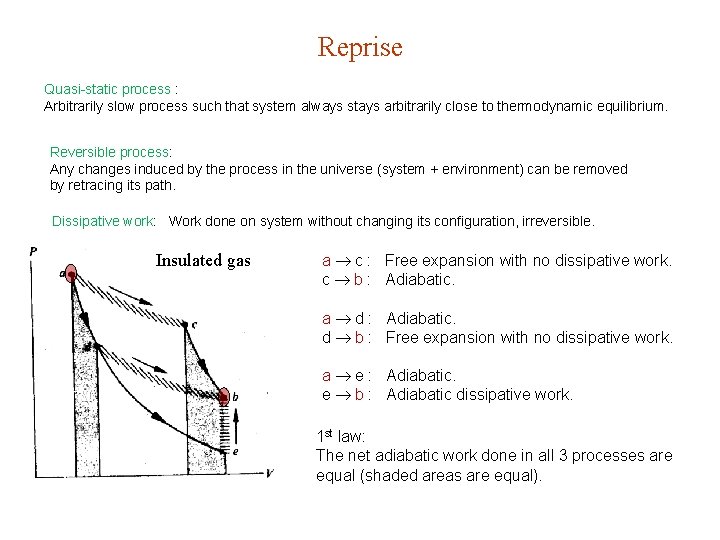
Reprise Quasi-static process : Arbitrarily slow process such that system always stays arbitrarily close to thermodynamic equilibrium. Reversible process: Any changes induced by the process in the universe (system + environment) can be removed by retracing its path. Dissipative work: Work done on system without changing its configuration, irreversible. Insulated gas a c : Free expansion with no dissipative work. c b : Adiabatic. a d : Adiabatic. d b : Free expansion with no dissipative work. a e : Adiabatic. e b : Adiabatic dissipative work. 1 st law: The net adiabatic work done in all 3 processes are equal (shaded areas are equal).