17 Group Theory 1 Introduction to Group Theory

17. Group Theory 1. Introduction to Group Theory 2. Representation of Groups 3. Symmetry & Physics 4. Discrete Groups 5. Direct Products 6. Symmetric Groups 7. Continuous Groups 8. Lorentz Group 9. Lorentz Covariance of Maxwell’s Equations 10. Space Groups

1. Introduction to Group Theory Symmetry : 1. Spatial symmetry of crystals ~ X-ray diffraction patterns. 2. Spatial symmetry of molecules ~ Selection rules in vibrational spectra. 3. Symmetry of periodic systems ~ e-properties: energy bands, conductivity, … Invariance under transformations : 1. Linear displacement ~ Conservation of (linear) momentum. 2. Rotation ~ Conservation of angular momentum. 3. Between (inertial) frames ~ General (special) relativity. Theories of elementary particles begin with symmetries & conservation laws. Group theory was invented to handle symmetries & invariance.

Definition of a Group Refs: W. K. Tung, “Group Theory in Physics” (85) M. Tinkham, “Group Theory & QM” (64) A group { G, } is a set G with a multiplication such that a, b, c G , 1. Closure 2. Associativity 3. Identity 4. Inverse Group { G, } is usually called simply group G and a b, ab. Two easily proved theorems : 1. Every a 1 is unique. 2. Rearrangement theorem

More Definitions Finite group : Group with a finite number n of elements. n = order of the group. Discrete group : 1 -1 map between set G & a subset of the natural number. ( label of elements of G is discrete ) Continuous group with n-parameter : 1 -1 map between set G & subset of Rn. Abelian group : is commutative, i. e. , Cyclic group Cn of order n : Cn is abelian Group {G, } is homomorphic to group { H , } : a map f : G H that preserves multiplications, i. e. , If f is 1 -1 onto ( f 1 exists ), then {G, } and { H , } are isomorphic. Subgroup of group {G, } : Subset of G that is closed under .

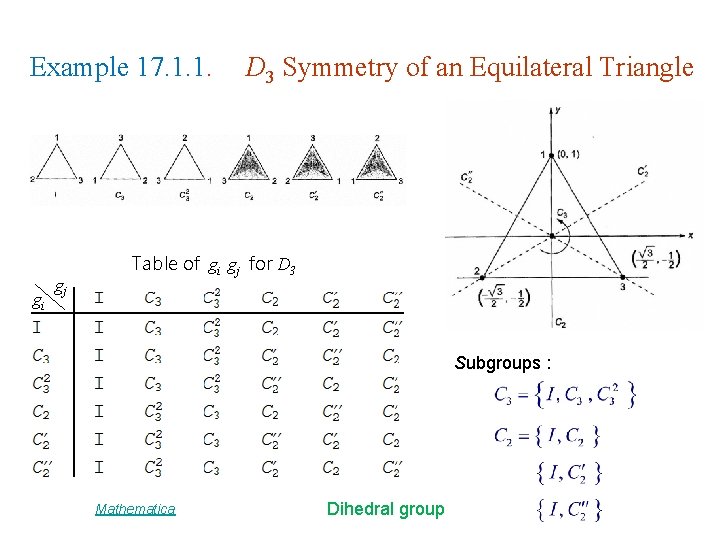
Example 17. 1. 1. gi gj D 3 Symmetry of an Equilateral Triangle Table of gi gj for D 3 Subgroups : Mathematica Dihedral group

Example 17. 1. 2. Rotation of a Circular Disk Rotation in x-y plane by angle : 1 -D continuous abelian group.

Example 17. 1. 3. An Abstarct Group An abstract group is defined by its multiplication table alone. Vierergruppe (4 -group) :

Example 17. 1. 4. Isomorphism & Homomorphism: C 4 = Group of symmetry operations of a square that can’t be flipped. abelian C 4 & G are isomorphic. Subgroup:

2. Representation of Groups A representation of a group is a set of linear transformations on a vector space that obey the same multiplication table as the group. Matrix representation : Representation in which the linear transformations tak the form of invertible matrices ( done by choosing a particular basis for the vector space ). Unitary representation : Representation by unitary matrices. Every matrix representation is isomorphic to a unitary reprsentation.

Example 17. 2. 1. Unitary representations for A Unitary Representation :

More Definitions & Properties A representation U(G) is faithful if U(G) is isomorphic to G. Every group has a trivial representation with Let U(G) be a representation of G, then is also a representation. W(G) & U(G) are equivalent representations : A representation U(G) is reducible if every U(g) is equivalent to the same block diagonal form, i. e. , for some We then write : W 1 A representation U(G) is irreducible if it is not reducible. Commuting matrices can be simultaneously digonalized All irreducible representations (IRs) of an abelian group are 1 -D. W 2

Example 17. 2. 2. A Reducible Representation A reducible representation for Using & we get the equivalent block diagonal form : ,

Example 17. 2. 3. Representations of a Continuous Group Symmetry of a circular disk : G is abelian R is reducible. Let & Independent IRs : Only U 1 & U 1 are faithful.

3. Symmetry & Physics Let R be a tranformation operator such as rotation or translation. i. e. , is the tranformed hamiltonian & is the transformed wave function If H is invariant under R : i. e. , is also an eigenfunction with eigenvalue E. possibility of degeneracy. Actual degeneracy depends on the symmetry group of H & can be calculated, without solving the Schrodinger eq. , by means of the representation theory.

Starting with any function , we can generate a set Next, we orthonormalize S using, say, the Gram-Schmidt scheme, to get = basis that spans an d –D space. Or, in matrix form : i. e. , is a representation of G on the space spanned by .

Starting with any function , we can generate a basis for a d-D representation for G. U is in general reducible, i. e. , where m = number of blocks equivalent to the same IR U ( ). w. r. t. a basis for an IR of G. ( Shur’s lemma ) If is an eigenfunction of H, then U is an IR. For arbitary , we can take one state from each U ( ) block to get a basis to set up a matrix eigen-equation of H to calculate E.

Example 17. 3. 1. multiplication table An Even H H is even in x Let be the operator then IR Cs is abelian All IRs are 1 -D. For an arbitrary (x) : Mathematica = basis for W Even Odd

Generation of IR Basis Using Schur’s lemma, one can show that (Tung, § 4. 2) where P ( ) = projector onto the space of unitary IR U ( ) (g) = Character (trace) of U ( ) (g). n = dimension of IR. n. G = order of G. R(g) = operator corresponding to g. For any f (x), , if not empty, is the ith basis vector for the IR U ( ). , if not empty, is a basis vector for the IR U ( ).

Example 17. 3. 2. QM: Triangular Symmetry 3 atoms at vertices Ri of an equilaterial triangle : Starting with atomic s-wave function (r 1) at R 1 :

4. Discrete Groups Classes : For any a G, the set is called a class of G. C is usually identified by one of its elements. Rearrangement theorem A class can be generated by any one of its members. ( a can be any member of C ).

Example 17. 4. 1. g a Classes of D 3 Table of g a g 1 for D 3 Classes of D 3 are : Usually denoted as Mathematica Orthogonality relations : All members of a class have the same character(trace). Dimensionality theorem :

Normalized full representation table of D 3 : Take each row (column) as vector : They’re all orthonormalized. Sum over column (row) then gives the completeness condition.

Example 17. 4. 2. row orthogonality A 1 , E : E, E: Completeness C 3 , C 2 : C 3 , C 3 : Orthogonality Relations: D 3 Character table of D 3 Mathematica

Example 17. 4. 3. Counting IRs multiplication table C 4 Table of g b g 1 for C 4 g b Character table C 4

Example 17. 4. 4. Decomposing a Reducible Representation

Other Discrete Groups

5. Direct Products

6. Symmetric Groups

7. Continuous Groups

8. Lorentz Group

9. Lorentz Covariance of Maxwell’s Equations

10. Space Groups