17 Chemical Equilibrium 1 Chapter Goals 1 Basic

17 Chemical Equilibrium 1

Chapter Goals 1. Basic Concepts 2. The Equilibrium Constant 3. Variation of Kc with the Form of the Balanced Equation 4. The Reaction Quotient 5. Uses of the Equilibrium Constant, Kc 6. Disturbing a System at Equilibrium: Predictions 2

Chapter Goals 7. The Haber Process: A Commercial Application of Equilibrium 8. Disturbing a System at Equilibrium: Calculations 9. Partial Pressures and the Equilibrium Constant 10. Relationship between Kp and Kc 11. Heterogeneous Equilibria 3

Chapter Goals 12. Relationship between Gorxn and the Equilibrium Constant 13. Evaluation of Equilibrium Constants at Different Temperatures 4

Basic Concepts • Reversible reactions do not go to completion. – They can occur in either direction – Symbolically, this is represented as: 5

Basic Concepts • Chemical equilibrium exists when two opposing reactions occur simultaneously at the same rate. – A chemical equilibrium is a reversible reaction that the forward reaction rate is equal to the reverse reaction rate. • Chemical equilibria are dynamic equilibria. – Molecules are continually reacting, even though the overall composition of the reaction mixture does not change. 6

Basic Concepts • One example of a dynamic equilibrium can be shown using radioactive 131 I as a tracer in a saturated Pb. I 2 solution. 7

Basic Concepts • This movie depicts a dynamic equilibrium. 8

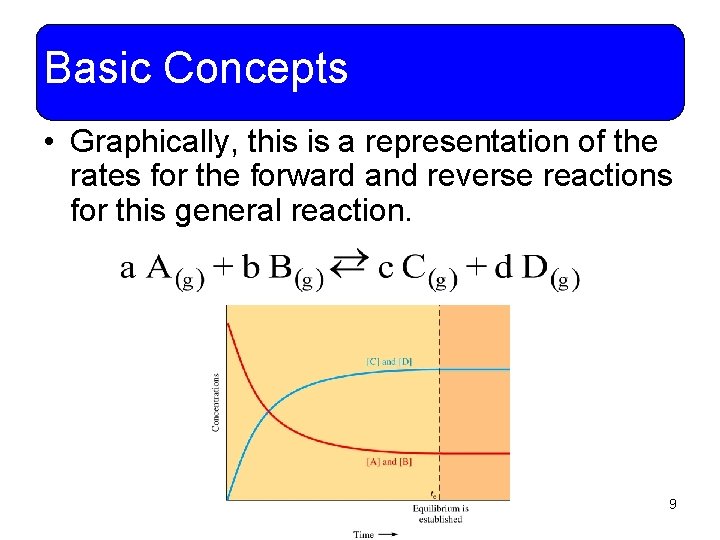
Basic Concepts • Graphically, this is a representation of the rates for the forward and reverse reactions for this general reaction. 9

Basic Concepts • One of the fundamental ideas of chemical equilibrium is that equilibrium can be established from either the forward or reverse direction. 10

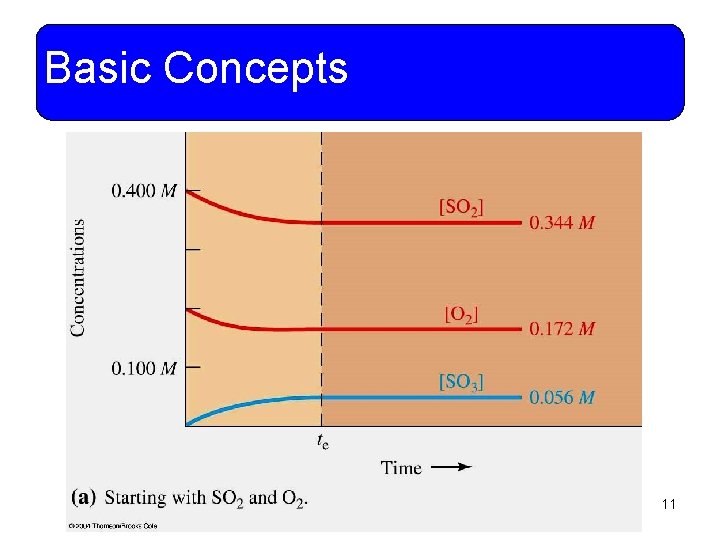
Basic Concepts 11

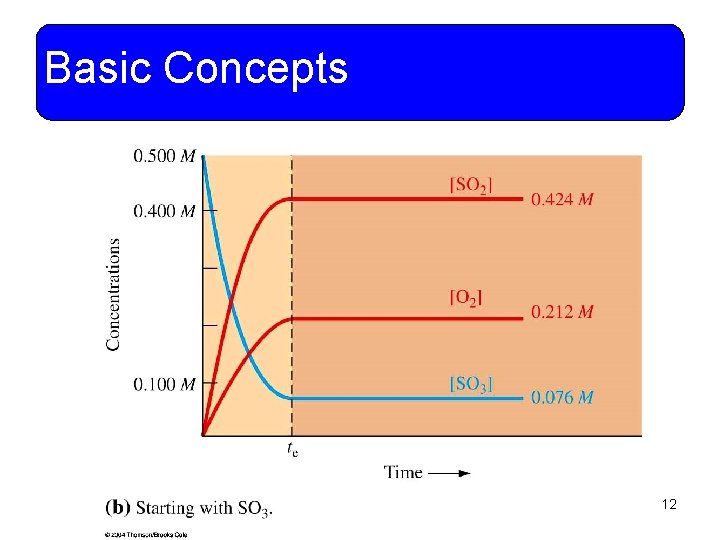
Basic Concepts 12

The Equilibrium Constant • For a simple one-step mechanism reversible reaction such as: • The rates of the forward and reverse reactions can be represented as: 13

The Equilibrium Constant • When system is at equilibrium: Ratef = Rater 14

The Equilibrium Constant • Because the ratio of two constants is a constant we can define a new constant as follows : 15

The Equilibrium Constant • Similarly, for the general reaction: we can define a constant 16

The Equilibrium Constant • Kc is the equilibrium constant. • Kc is defined for a reversible reaction at a given temperature as the product of the equilibrium concentrations (in M) of the products, each raised to a power equal to its stoichiometric coefficient in the balanced equation, divided by the product of the equilibrium concentrations (in M) of the reactants, each raised to a power equal to its stoichiometric coefficient in the 17 balanced equation.

The Equilibrium Constant • Example 17 -1: Write equilibrium constant expressions for the following reactions at 500 o. C. All reactants and products are gases at 500 o. C. 18

The Equilibrium Constant 19

The Equilibrium Constant 20

The Equilibrium Constant 21

The Equilibrium Constant 22

The Equilibrium Constant • Equilibrium constants are dimensionless because they actually involve a thermodynamic quantity called activity. – Activities are directly related to molarity 23

The Equilibrium Constant • Example 17 -2: One liter of equilibrium mixture from the following system at a high temperature was found to contain 0. 172 mole of phosphorus trichloride, 0. 086 mole of chlorine, and 0. 028 mole of phosphorus pentachloride. Calculate Kc for the reaction. • Equil []’s 0. 028 M 0. 172 M You do it! 0. 086 M 24

The Equilibrium Constant 25

The Equilibrium Constant • Example 17 -3: The decomposition of PCl 5 was studied at another temperature. One mole of PCl 5 was introduced into an evacuated 1. 00 liter container. The system was allowed to reach equilibrium at the new temperature. At equilibrium 0. 60 mole of PCl 3 was present in the container. Calculate the equilibrium constant at this temperature. 26

The Equilibrium Constant 27

The Equilibrium Constant 28

The Equilibrium Constant 29

The Equilibrium Constant 30

The Equilibrium Constant • Example 17 -4: At a given temperature 0. 80 mole of N 2 and 0. 90 mole of H 2 were placed in an evacuated 1. 00 -liter container. At equilibrium 0. 20 mole of NH 3 was present. Calculate Kc for the reaction. You do it! 31

The Equilibrium Constant 32

Variation of Kc with the Form of the Balanced Equation • The value of Kc depends upon how the balanced equation is written. • From example 17 -2 we have this reaction: • This reaction has a Kc=[PCl 3][Cl 2]/[PCl 5]=0. 53 33

Variation of Kc with the Form of the Balanced Equation • Example 17 -5: Calculate the equilibrium constant for the reverse reaction by two methods, i. e, the equilibrium constant for this reaction. Equil. []’s 0. 172 M 0. 086 M 0. 028 M The concentrations are from Example 17 -2. 34

Variation of Kc with the Form of the Balanced Equation 35

Variation of Kc with the Form of the Balanced Equation 36

Variation of Kc with the Form of the Balanced Equation Large equilibrium constants indicate that most of the reactants are converted to products. Ø Small equilibrium constants indicate that only small amounts of products are formed. Ø 37

The Reaction Quotient 38

The Reaction Quotient 39

The Reaction Quotient • The mass action expression or reaction quotient has the symbol Q. – Q has the same form as Kc • The major difference between Q and Kc is that the concentrations used in Q are not necessarily equilibrium values. 40

The Reaction Quotient • Why do we need another “equilibrium constant” that does not use equilibrium concentrations? • Q will help us predict how the equilibrium will respond to an applied stress. • To make this prediction we compare Q with Kc. 41

The Reaction Quotient 42

The Reaction Quotient • Example 17 -6: The equilibrium constant for the following reaction is 49 at 450 o. C. If 0. 22 mole of I 2, 0. 22 mole of H 2, and 0. 66 mole of HI were put into an evacuated 1. 00 -liter container, would the system be at equilibrium? If not, what must occur to establish equilibrium? 43

Uses of the Equilibrium Constant, Kc • Example 17 -7: The equilibrium constant, Kc, is 3. 00 for the following reaction at a given temperature. If 1. 00 mole of SO 2 and 1. 00 mole of NO 2 are put into an evacuated 2. 00 L container and allowed to reach equilibrium, what will be the concentration of each compound at equilibrium? 44

Uses of the Equilibrium Constant, Kc 45

Uses of the Equilibrium Constant, Kc 46

Uses of the Equilibrium Constant, Kc 47

Uses of the Equilibrium Constant, Kc 48

Uses of the Equilibrium Constant, Kc 49

Uses of the Equilibrium Constant, Kc • Example 17 -8: The equilibrium constant is 49 for the following reaction at 450 o. C. If 1. 00 mole of HI is put into an evacuated 1. 00 -liter container and allowed to reach equilibrium, what will be the equilibrium concentration of each substance? 50

Uses of the Equilibrium Constant, Kc 51

Disturbing a System at Equlibrium: Predictions • Le. Chatelier’s Principle - If a change of conditions (stress) is applied to a system in equilibrium, the system responds in the way that best tends to reduce the stress in reaching a new state of equilibrium. – • We first encountered Le. Chatelier’s Principle in Chapter 14. Some possible stresses to a system at equilibrium are: 1. Changes in concentration of reactants or products. 2. Changes in pressure or volume (for gaseous reactions) 3. Changes in temperature. 52

Disturbing a System at Equlibrium: Predictions • For convenience we may express the amount of a gas in terms of its partial pressure rather than its concentration. • To derive this relationship, we must solve the ideal gas equation. 53

Disturbing a System at Equlibrium: Predictions 1 Changes in Concentration of Reactants and/or Products • – Also true for changes in pressure for reactions involving gases. Look at the following system at equilibrium at 450 o. C. 54

Disturbing a System at Equlibrium: Predictions 1 Changes in Concentration of Reactants and/or Products • – Also true for changes in pressure for reactions involving gases. Look at the following system at equilibrium at 450 o. C. 55

Disturbing a System at Equlibrium: Predictions 1 Changes in Concentration of Reactants and/or Products • – Also true for changes in pressure for reactions involving gases. Look at the following system at equilibrium at 450 o. C. 56

Disturbing a System at Equlibrium: Predictions 2 Changes in Volume • (and pressure for reactions involving gases) – Predict what will happen if the volume of this system at equilibrium is changed by changing the pressure at constant temperature: 57

Disturbing a System at Equlibrium: Predictions 58

Disturbing a System at Equlibrium: Predictions 59

Disturbing a System at Equlibrium: Predictions 60

Disturbing a System at Equlibrium: Predictions 3 Changing the Temperature 61

Disturbing a System at Equlibrium: Predictions 3 Changing the Reaction Temperature – Consider the following reaction at equilibrium: 62

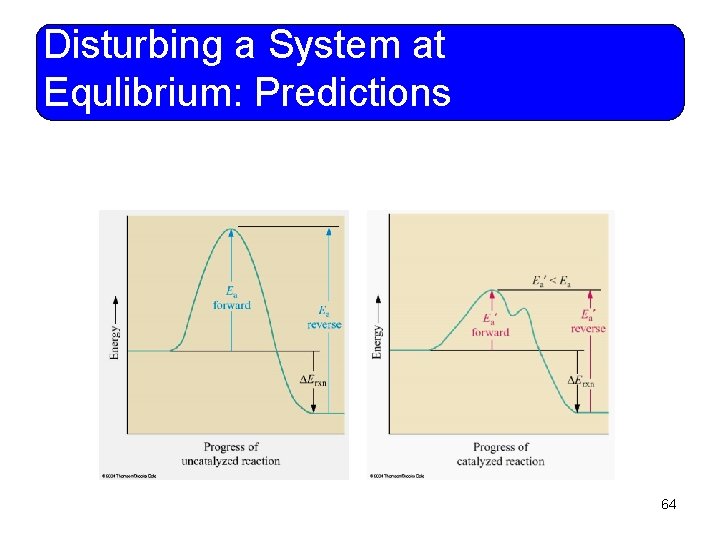
Disturbing a System at Equlibrium: Predictions • Introduction of a Catalyst – Catalysts decrease the activation energy of both the forward and reverse reaction equally. • Catalysts do not affect the position of equilibrium. – The concentrations of the products and reactants will be the same whether a catalyst is introduced or not. – Equilibrium will be established faster with a catalyst. 63

Disturbing a System at Equlibrium: Predictions 64

Disturbing a System at Equlibrium: Predictions • Example 17 -9: Given the reaction below at equilibrium in a closed container at 500 o. C. How would the equilibrium be influenced by the following? 65

Disturbing a System at Equlibrium: Predictions • Example 17 -10: How will an increase in pressure (caused by decreasing the volume) affect the equilibrium in each of the following reactions? 66

Disturbing a System at Equlibrium: Predictions • Example 17 -11: How will an increase in temperature affect each of the following reactions? 67

The Haber Process: A Practical Application of Equilibrium • The Haber process is used for the commercial production of ammonia. – This is an enormous industrial process in the US and many other countries. – Ammonia is the starting material for fertilizer production. • Look at Example 17 -9. What conditions did we predict would be most favorable for the production of ammonia? 68

The Haber Process: A Practical Application of Equilibrium 69

The Haber Process: A Practical Application of Equilibrium 70

The Haber Process: A Practical Application of Equilibrium • This diagram illustrates the commercial system devised for the Haber process. 71

Disturbing a System at Equilibrium: Calculations • To help with the calculations, we must determine the direction that the equilibrium will shift by comparing Q with Kc. • Example 17 -12: An equilibrium mixture from the following reaction was found to contain 0. 20 mol/L of A, 0. 30 mol/L of B, and 0. 30 mol/L of C. What is the value of Kc for this reaction? 72

Disturbing a System at Equilibrium: Calculations 73

Disturbing a System at Equilibrium: Calculations • If the volume of the reaction vessel were suddenly doubled while the temperature remained constant, what would be the new equilibrium concentrations? 1 Calculate Q, after the volume has been doubled 74

Disturbing a System at Equilibrium: Calculations • Since Q<Kc the reaction will shift to the right to re -establish the equilibrium. 2 Use algebra to represent the new concentrations. 75

Disturbing a System at Equilibrium: Calculations • Since Q<Kc the reaction will shift to the right to re -establish the equilibrium. 2 Use algebra to represent the new concentrations. 76

Disturbing a System at Equilibrium: Calculations • Since Q<Kc the reaction will shift to the right to re -establish the equilibrium. 2 Use algebra to represent the new concentrations. 77

Disturbing a System at Equilibrium: Calculations • Since Q<Kc the reaction will shift to the right to re -establish the equilibrium. 2 Use algebra to represent the new concentrations. 78

Disturbing a System at Equilibrium: Calculations 79

Disturbing a System at Equilibrium: Calculations 80

Disturbing a System at Equilibrium: Calculations 81

Disturbing a System at Equilibrium: Calculations • Example 17 -13: Refer to example 17 -12. If the initial volume of the reaction vessel were halved, while the temperature remains constant, what will the new equilibrium concentrations be? Recall that the original concentrations were: [A]=0. 20 M, [B]=0. 30 M, and [C]=0. 30 M. You do it! 82

Disturbing a System at Equilibrium: Calculations 83

Disturbing a System at Equilibrium: Calculations 84

Disturbing a System at Equilibrium: Calculations 85

Disturbing a System at Equilibrium: Calculations • Example 17 -14: A 2. 00 liter vessel in which the following system is in equilibrium contains 1. 20 moles of COCl 2, 0. 60 moles of CO and 0. 20 mole of Cl 2. Calculate the equilibrium constant. You do it! 86

Disturbing a System at Equilibrium: Calculations 87

Disturbing a System at Equilibrium: Calculations • An additional 0. 80 mole of Cl 2 is added to the vessel at the same temperature. Calculate the molar concentrations of CO, Cl 2, and COCl 2 when the new equilibrium is established. You do it! 88

Disturbing a System at Equilibrium: Calculations 89

Disturbing a System at Equilibrium: Calculations 90

Partial Pressures and the Equilibrium Constant • For gas phase reactions the equilibrium constants can be expressed in partial pressures rather than concentrations. • For gases, the pressure is proportional to the concentration. • We can see this by looking at the ideal gas law. – – PV = n. RT P = n. RT/V n/V = M P= MRT and M = P/RT 91

Partial Pressures and the Equilibrium Constant • Consider this system at equilibrium at 5000 C. 92

Partial Pressures and the Equilibrium Constant 93

Relationship Between Kp and Kc • From the previous slide we can see that the relationship between Kp and Kc is: 94

Relationship Between Kp and Kc • Example 17 -15: Nitrosyl bromide, NOBr, is 34% dissociated by the following reaction at 25 o. C, in a vessel in which the total pressure is 0. 25 atmosphere. What is the value of Kp? 95

Relationship Between Kp and Kc 96

Relationship Between Kp and Kc 97

Relationship Between Kp and Kc 98

Relationship Between Kp and Kc • The numerical value of Kc for this reaction can be determined from the relationship of Kp and Kc. 99

Relationship Between Kp and Kc • Example 17 -16: Kc is 49 for the following reaction at 450 o. C. If 1. 0 mole of H 2 and 1. 0 mole of I 2 are allowed to reach equilibrium in a 3. 0 -liter vessel, (a) How many moles of I 2 remain unreacted at equilibrium? You do it! 100

Relationship Between Kp and Kc 101

Relationship Between Kp and Kc (b) What are the equilibrium partial pressures of H 2, I 2 and HI? You do it! 102

Relationship Between Kp and Kc 103

Relationship Between Kp and Kc (c) What is the total pressure in the reaction vessel? You do it! 104

Relationship Between Kp and Kc 105

Heterogeneous Equlibria • Heterogeneous equilibria have more than one phase present. – For example, a gas and a solid or a liquid and a gas. • How does the equilibrium constant differ for heterogeneous equilibria? – Pure solids and liquids have activities of unity. – Solvents in very dilute solutions have activities that are essentially unity. – The Kc and Kp for the reaction shown above are: 106

Heterogeneous Equlibria 107

Heterogeneous Equlibria • What are Kc and Kp for this reaction? You do it! 108

Heterogeneous Equlibria • What are Kc and Kp for this reaction? 109

o G Relationship Between rxn and the Equilibrium Constant • Gorxn is the standard free energy change. – Gorxn is defined for the complete conversion of all reactants to all products. • G is the free energy change at nonstandard conditions • For example, concentrations other than 1 M or pressures other than 1 atm. • G is related to Go by the following relationship. 110

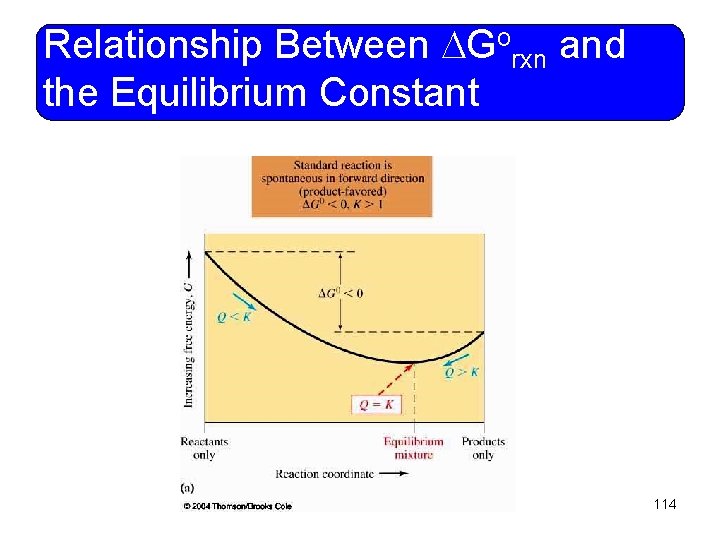
o G Relationship Between rxn and the Equilibrium Constant • At equilibrium, G=0 and Q=Kc. • Then we can derive this relationship: 111

o G Relationship Between rxn and the Equilibrium Constant • For the following generalized reaction, thermodynamic equilibrium constant is defined as follows: 112

o G Relationship Between rxn and the Equilibrium Constant • The relationships among Gorxn, K, and the spontaneity of a reaction are: Gorxn K <0 >1 Spontaneity at unit concentration Forward reaction spontaneous =0 =1 System at equilibrium >0 <1 Reverse reaction spontaneous 113

Relationship Between Gorxn and the Equilibrium Constant 114

o G Relationship Between rxn and the Equilibrium Constant • Example 17 -17: Calculate the equilibrium constant, Kp, for the following reaction at 25 o. C from thermodynamic data in Appendix K. • Note: this is a gas phase reaction. 115

o G Relationship Between rxn and the Equilibrium Constant 116

o G Relationship Between rxn and the Equilibrium Constant 117

o G Relationship Between rxn and the Equilibrium Constant • Kp for the reverse reaction at 25 o. C can be calculated easily, it is the reciprocal of the above reaction. 118

o G Relationship Between rxn and the Equilibrium Constant • Example 17 -18: At 25 o. C and 1. 00 atmosphere, Kp = 4. 3 x 10 -13 for the decomposition of NO 2. Calculate Gorxn at 25 o. C. You do it. 119

o G Relationship Between rxn and the Equilibrium Constant 120

o G Relationship Between rxn and the Equilibrium Constant • The relationship for K at conditions other than thermodynamic standard state conditions is derived from this equation. 121

Evaluation of Equilibrium Constants at Different Temperatures • From the value of Ho and K at one temperature, T 1, we can use the van’t Hoff equation to estimate the value of K at another temperature, T 2. 122

Evaluation of Equilibrium Constants at Different Temperatures • Example 17 -19: For the reaction in example 1718, Ho = 114 k. J/mol and Kp = 4. 3 x 10 -13 at 25 o. C. Estimate Kp at 250 o. C. 123

Evaluation of Equilibrium Constants at Different Temperatures 124

Evaluation of Equilibrium Constants at Different Temperatures 125

17 Chemical Equilibrium 126