17 6 MHS e movimento circular uniforme MHS

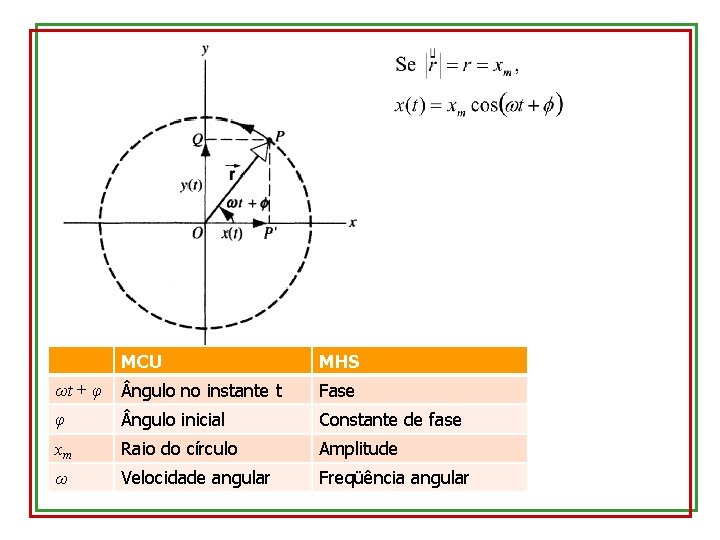
17. 6 – MHS e movimento circular uniforme MHS pode ser visto como a projeção do MCU em um dos eixos cartesianos Galileu e as luas de Júpiter

MCU MHS ωt + φ ngulo no instante t Fase φ ngulo inicial Constante de fase xm Raio do círculo Amplitude ω Velocidade angular Freqüência angular

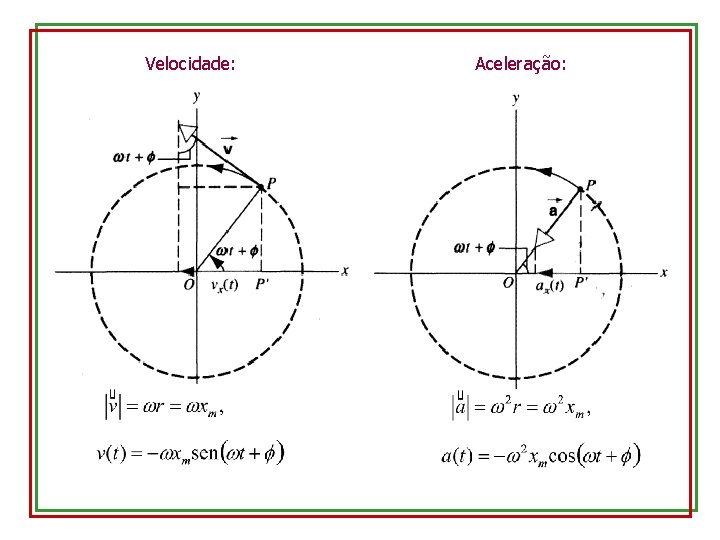
Velocidade: Aceleração:

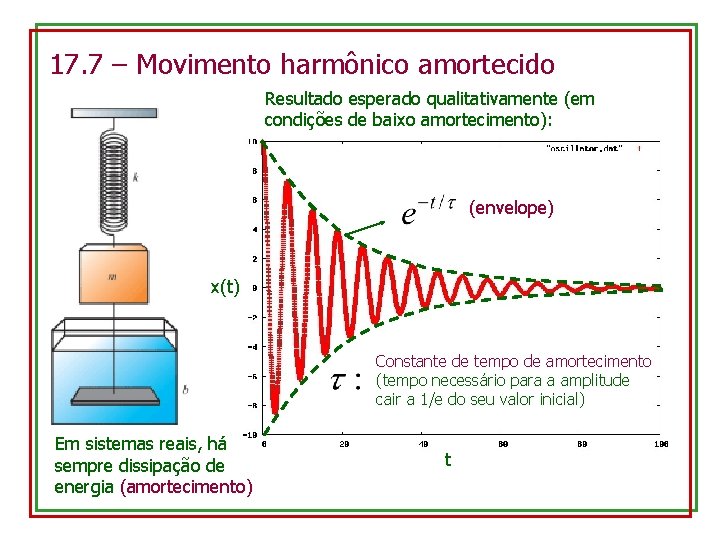
17. 7 – Movimento harmônico amortecido Resultado esperado qualitativamente (em condições de baixo amortecimento): (envelope) x(t) Constante de tempo de amortecimento (tempo necessário para a amplitude cair a 1/e do seu valor inicial) Em sistemas reais, há sempre dissipação de energia (amortecimento) t

Solução matemática: Para baixas velocidades a força de amortecimento pode ser aproximada por: (proporcional e contrária à velocidade) 2 a. Lei: Vamos propor a solução: Verificamos (quadro-negro) que esta é uma solução possível da equação diferencial nas seguintes condições: (amortecimento pequeno ou subcrítico) (tempo de amortecimento) (pequena redução da freqüência de oscilação em relação à freqüência natural)

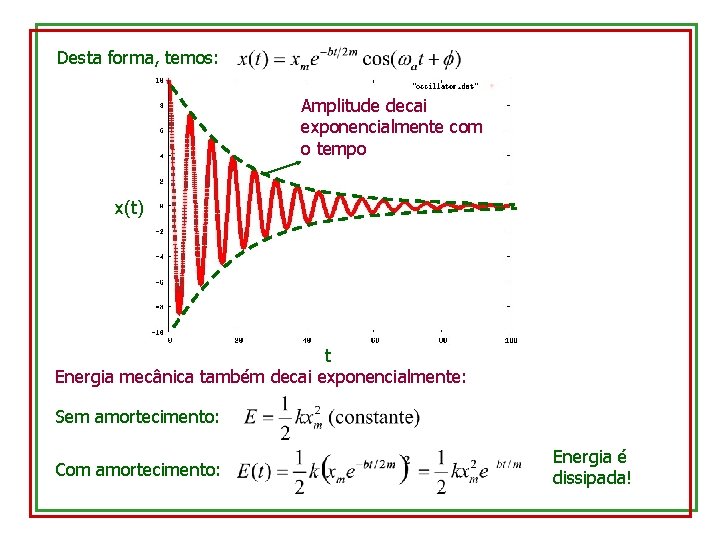
Desta forma, temos: Amplitude decai exponencialmente com o tempo x(t) t Energia mecânica também decai exponencialmente: Sem amortecimento: Com amortecimento: Energia é dissipada!

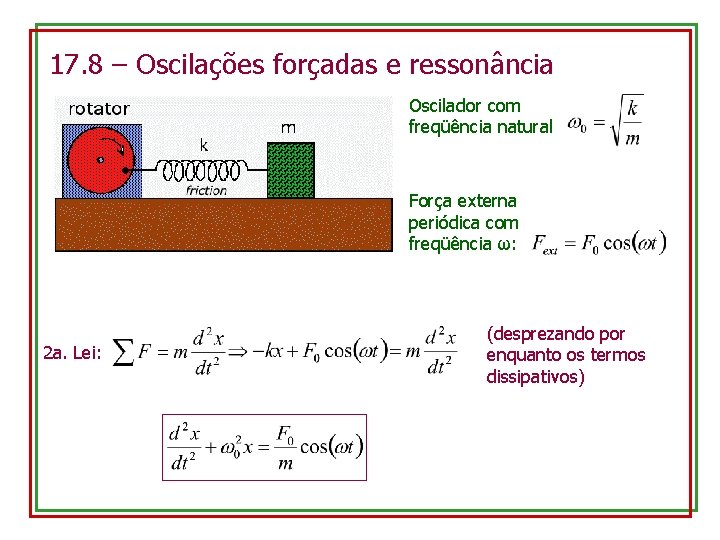
17. 8 – Oscilações forçadas e ressonância Oscilador com freqüência natural Força externa periódica com freqüência ω: 2 a. Lei: (desprezando por enquanto os termos dissipativos)

Precisamos resolver a equação diferencial: - Trata-se agora de uma equação inomogênea - Espera-se que a solução geral seja uma combinação de funções oscilatórias com freqüência ω0 e ω - Na presença de atrito, apenas a solução com freqüência ω vai sobreviver para tempos longos (regime estacionário) - A solução com freqüência ω0 vai desaparecer depois de um curto intervalo a partir do início do movimento (regime transiente) Assim, vamos tentar a seguinte solução particular: Substituindo na equação diferencial:

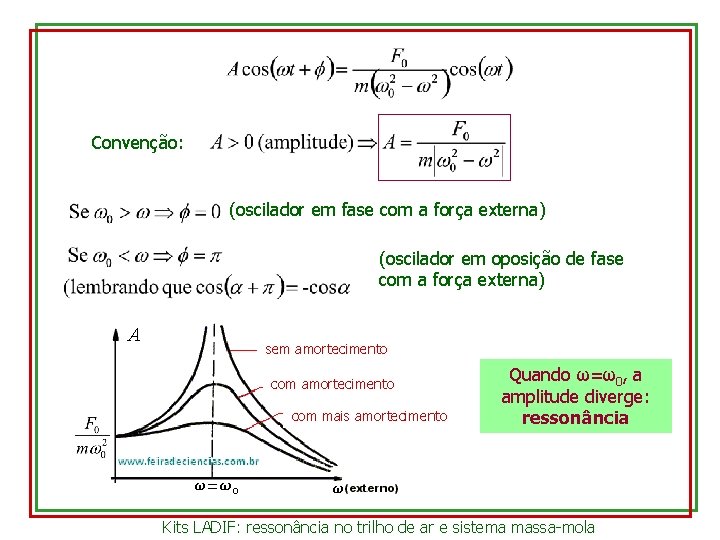
Convenção: (oscilador em fase com a força externa) (oscilador em oposição de fase com a força externa) A sem amortecimento com mais amortecimento Quando ω=ω0, a amplitude diverge: ressonância Kits LADIF: ressonância no trilho de ar e sistema massa-mola

A ponte de Tacoma http: //www. youtube. com/watch? v=P 0 Fi 1 Vcbp. AI

Quebrando um copo de vinho com som ressonante http: //www. youtube. com/watch? v=17 tq. Xgv. CN 0 E

17. 9 – Oscilações de dois corpos e modos normais Discussão qualitativa: Kit LADIF de pêndulos acoplados