17 2 Constructive and Destructive Interference of Sound

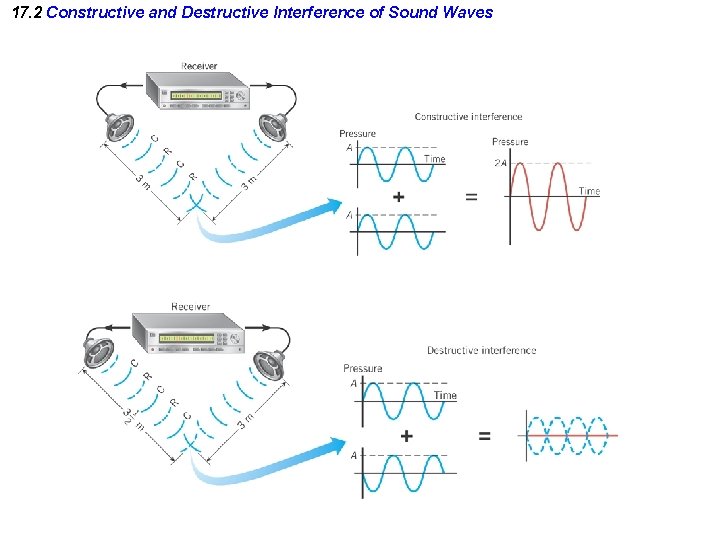
17. 2 Constructive and Destructive Interference of Sound Waves Example 1 What Does a Listener Hear? Two in-phase loudspeakers, A and B, are separated by 3. 20 m. A listener is stationed at C, which is 2. 40 m in front of speaker B. Both speakers are playing identical 214 -Hz tones, and the room temperature is 200 C. Does the listener hear a loud sound, or no sound?

17. 2 Constructive and Destructive Interference of Sound Waves Calculate the path length difference. Calculate the wavelength. Because the path length difference is equal to an integer (1) number of wavelengths, there is constructive interference, which means there is a loud sound.

17. 2 Constructive and Destructive Interference of Sound Waves

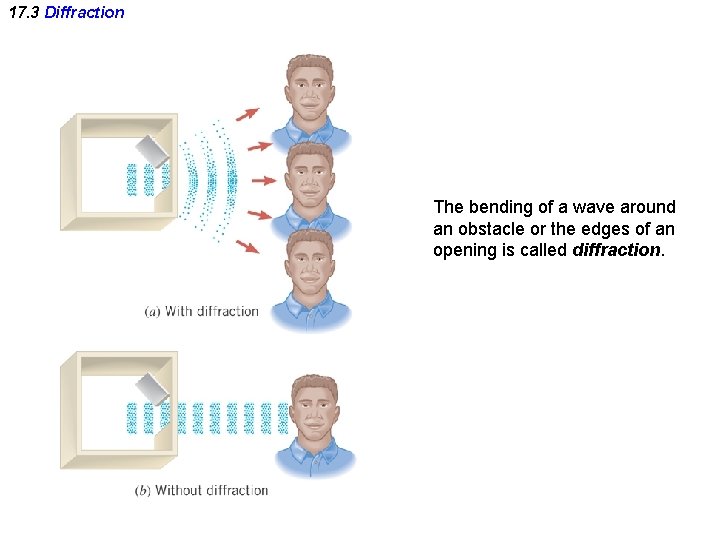
17. 3 Diffraction The bending of a wave around an obstacle or the edges of an opening is called diffraction.

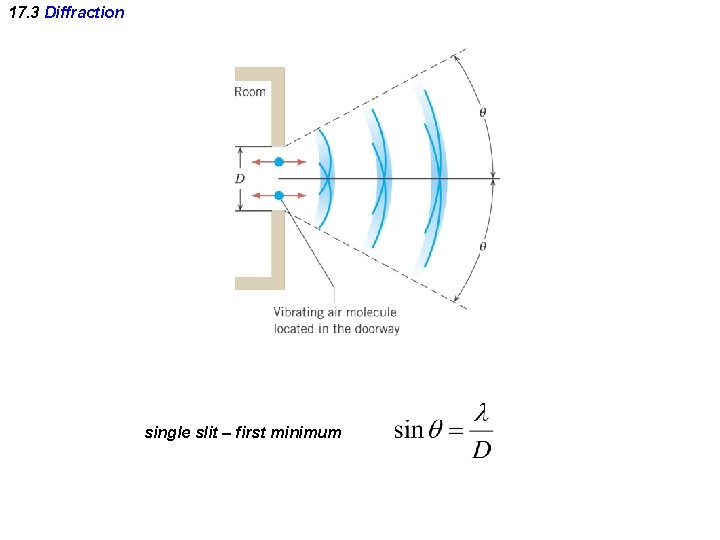
17. 3 Diffraction single slit – first minimum

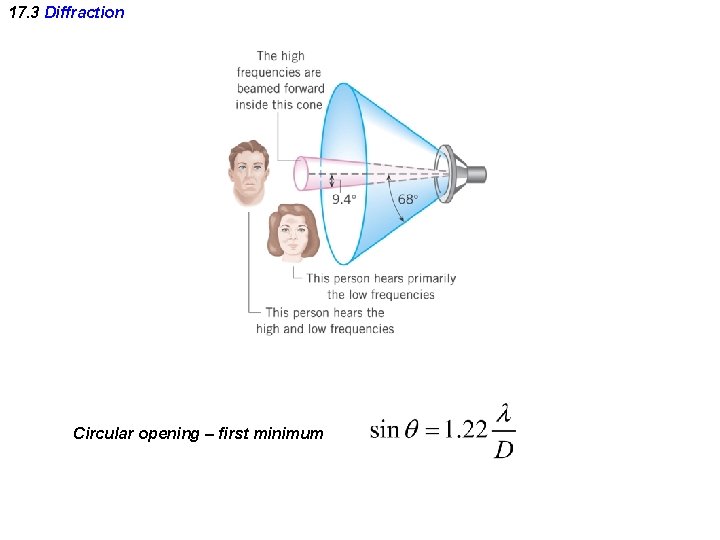
17. 3 Diffraction Circular opening – first minimum

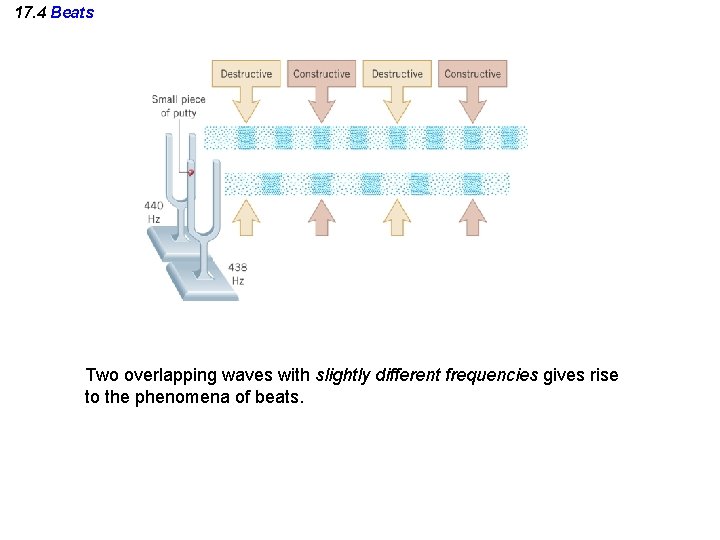
17. 4 Beats Two overlapping waves with slightly different frequencies gives rise to the phenomena of beats.

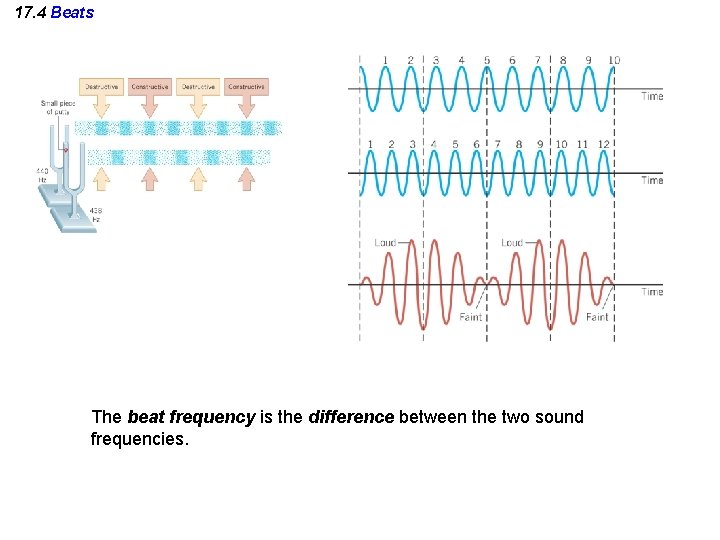
17. 4 Beats The beat frequency is the difference between the two sound frequencies.

Standing Wave Example

Standing Waves Note on Amplitudes • There are three types of amplitudes used in describing waves. – The amplitude of the individual waves, A – The amplitude of the simple harmonic motion of the elements in the medium, • 2 A sin kx • A given element in the standing wave vibrates within the constraints of the envelope function 2 A sin k x. – The amplitude of the standing wave, 2 A

Standing Waves, Definitions A node occurs at a point of zero amplitude. These correspond to positions of x where (every half wavelength) An antinode occurs at a point of maximum displacement, 2 A. These correspond to positions of x where (every quarter wavelength)

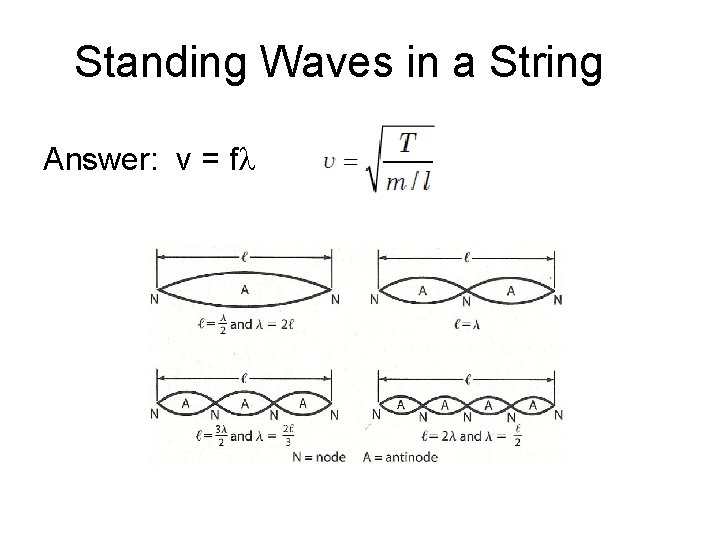
Standing Waves in a String Consider a string fixed at both ends having a length L. If Standing waves are set up by a continuous superposition of waves incident on and reflected from the ends, the ends of the strings must necessarily be nodes. Therefore there is a boundary condition on the waves. Question: What relationships (formulas) will be useful in determining the frequency of permissible standing wave patterns?

Standing Waves in a String Answer: v = f

Standing Waves in a String This is the first normal mode that is consistent with the boundary conditions. There are nodes at both ends. There is one antinode in the middle. This is the longest wavelength mode: ½l 1 = L so l 1 = 2 L The section of the standing wave between nodes is called a loop. In the first normal mode, the string vibrates in one loop.

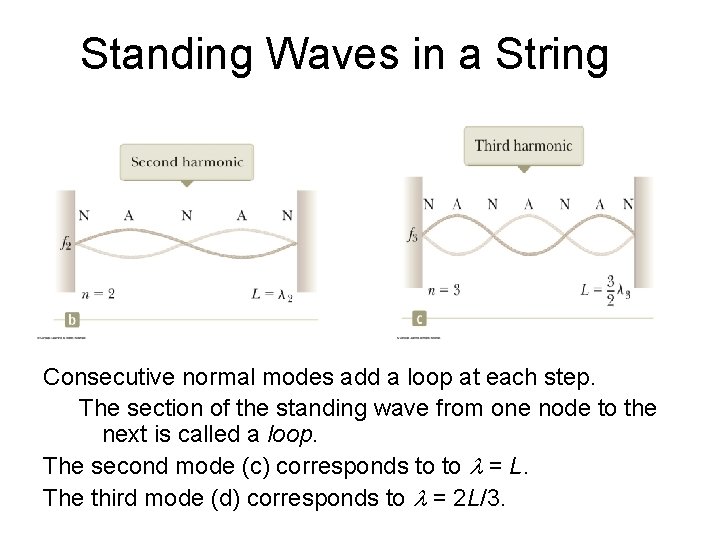
Standing Waves in a String Consecutive normal modes add a loop at each step. The section of the standing wave from one node to the next is called a loop. The second mode (c) corresponds to to l = L. The third mode (d) corresponds to l = 2 L/3.

Standing Waves on a String, Summary The wavelengths of the normal modes for a string of length L fixed at both ends are: n = 2 L / n n = 1, 2, 3, … n is the nth normal mode of oscillation The natural frequencies are

Waves on a String, Harmonic Series The fundamental frequency corresponds to n = 1. It is the lowest frequency, ƒ 1 The frequencies of the remaining natural modes are integer multiples of the fundamental frequency. ƒn = nƒ 1 Frequencies of normal modes that exhibit this relationship form a harmonic series. The normal modes are called harmonics.

Harmonics, Example A middle “C” string on a piano has a fundamental frequency of 262 Hz. What are the next two harmonics of this string? ƒ 1 = 262 Hz ƒ 2 = 2ƒ 1 = 524 Hz ƒ 3 = 3ƒ 1 = 786 Hz

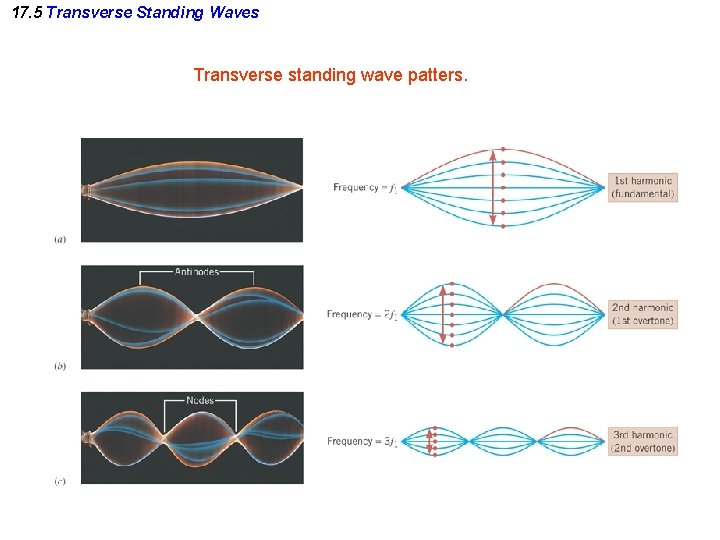
17. 5 Transverse Standing Waves Transverse standing wave patters.

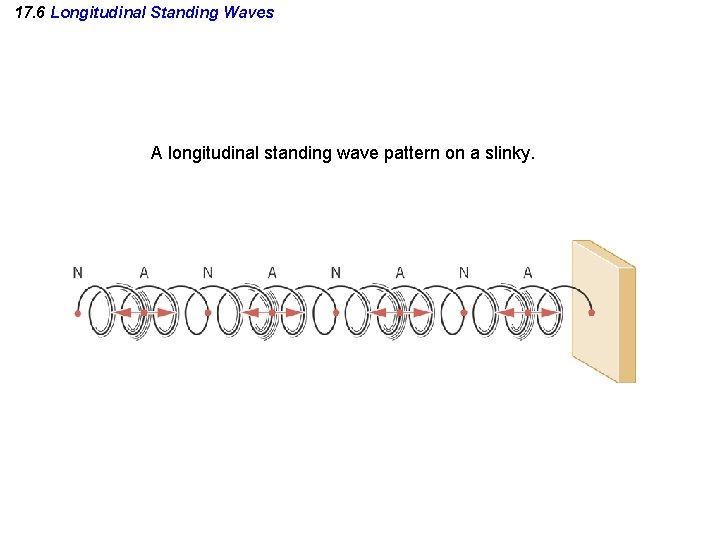
17. 6 Longitudinal Standing Waves A longitudinal standing wave pattern on a slinky.

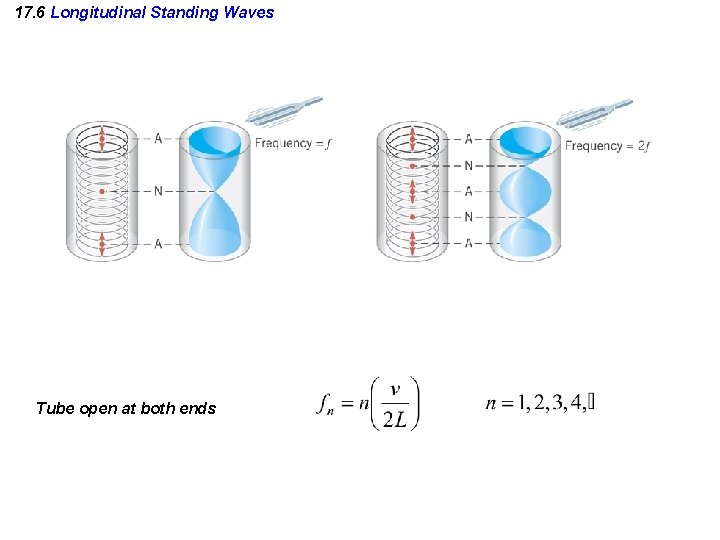
17. 6 Longitudinal Standing Waves Tube open at both ends

17. 6 Longitudinal Standing Waves Example 6 Playing a Flute When all the holes are closed on one type of flute, the lowest note it can sound is middle C (261. 6 Hz). If the speed of sound is 343 m/s, and the flute is assumed to be a cylinder open at both ends, determine the distance L.

17. 6 Longitudinal Standing Waves

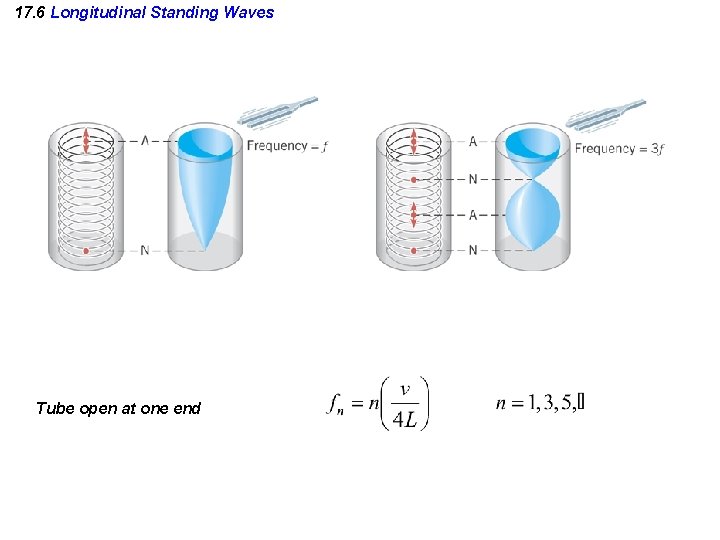
17. 6 Longitudinal Standing Waves Tube open at one end

Standing Waves in Air Columns • Standing waves can be set up in air columns as the result of interference between longitudinal sound waves traveling in opposite directions • The phase relationship between the incident and reflected waves depends upon whether the end of the pipe is opened or closed • Waves under boundary conditions model can be applied

Standing Waves in Air Columns, Closed End • A closed end of a pipe is a displacement node in the standing wave – The rigid barrier at this end will not allow longitudinal motion in the air • The closed end corresponds with a pressure antinode – It is a point of maximum pressure variations – The pressure wave is 90 o out of phase with the displacement wave

Standing Waves in Air Columns, Open End • The open end of a pipe is a displacement antinode in the standing wave – As the compression region of the wave exits the open end of the pipe, the constraint of the pipe is removed and the compressed air is free to expand into the atmosphere • The open end corresponds with a pressure node – It is a point of no pressure variation

Standing Waves in an Open Tube • Both ends are displacement antinodes • The fundamental frequency is v/2 L – This corresponds to the first diagram • The higher harmonics are ƒn = nƒ 1 = n (v/2 L) where n = 1, 2, 3, …

Standing Waves in a Tube Closed at One End • • The closed end is a displacement node The open end is a displacement antinode The fundamental corresponds to ¼l The frequencies are ƒn = nƒ = n (v/4 L) where n = 1, 3, 5, …

Standing Waves in Air Columns, Summary • In a pipe open at both ends, the natural frequencies of oscillation form a harmonic series that includes all integral multiples of the fundamental frequency • In a pipe closed at one end, the natural frequencies of oscillations form a harmonic series that includes only odd integral multiples of the fundamental frequency

Notes About Instruments • As the temperature rises: – Sounds produced by air columns become sharp • Higher frequency • Higher speed due to the higher temperature – Sounds produced by strings become flat • Lower frequency • The strings expand due to the higher temperature • As the strings expand, their tension decreases

More About Instruments • Musical instruments based on air columns are generally excited by resonance • The air column is presented with a sound wave rich in many frequencies • The sound is provided by: – A vibrating reed in woodwinds – Vibrations of the player’s lips in brasses – Blowing over the edge of the mouthpiece in a flute

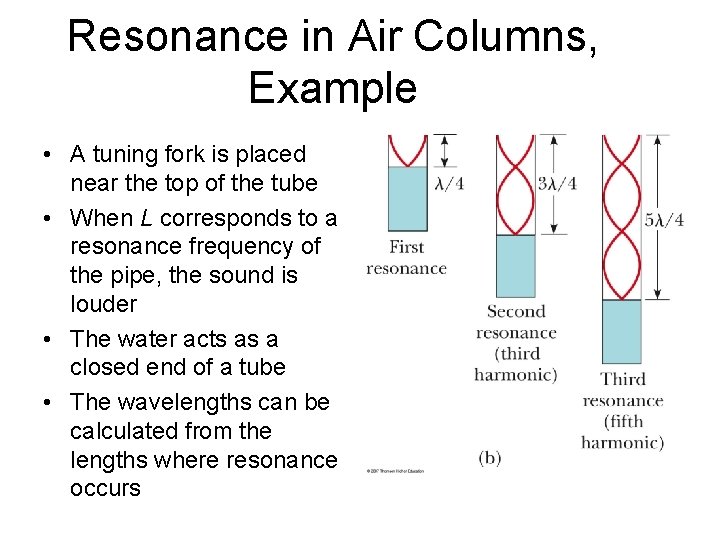
Resonance in Air Columns, Example • A tuning fork is placed near the top of the tube • When L corresponds to a resonance frequency of the pipe, the sound is louder • The water acts as a closed end of a tube • The wavelengths can be calculated from the lengths where resonance occurs