16 VECTOR CALCULUS VECTOR CALCULUS 16 8 Stokes

16 VECTOR CALCULUS

VECTOR CALCULUS 16. 8 Stokes’ Theorem In this section, we will learn about: The Stokes’ Theorem and using it to evaluate integrals.

STOKES’ VS. GREEN’S THEOREM Stokes’ Theorem can be regarded as a higher-dimensional version of Green’s Theorem. § Green’s Theorem relates a double integral over a plane region D to a line integral around its plane boundary curve. § Stokes’ Theorem relates a surface integral over a surface S to a line integral around the boundary curve of S (a space curve).

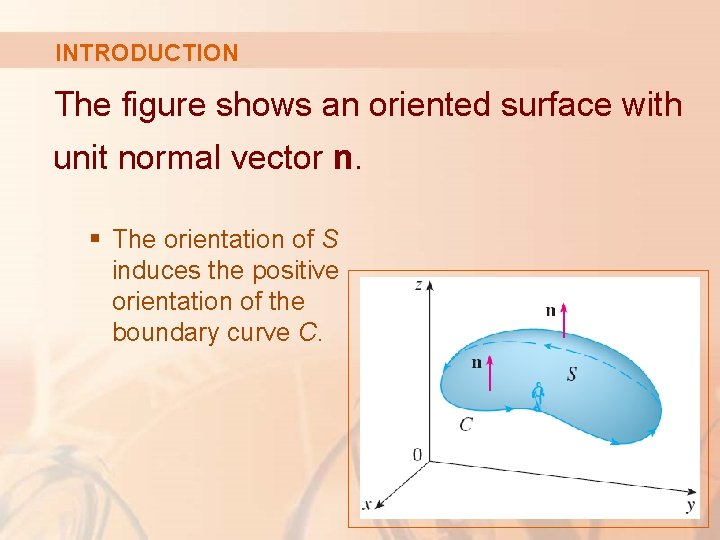
INTRODUCTION The figure shows an oriented surface with unit normal vector n. § The orientation of S induces the positive orientation of the boundary curve C.

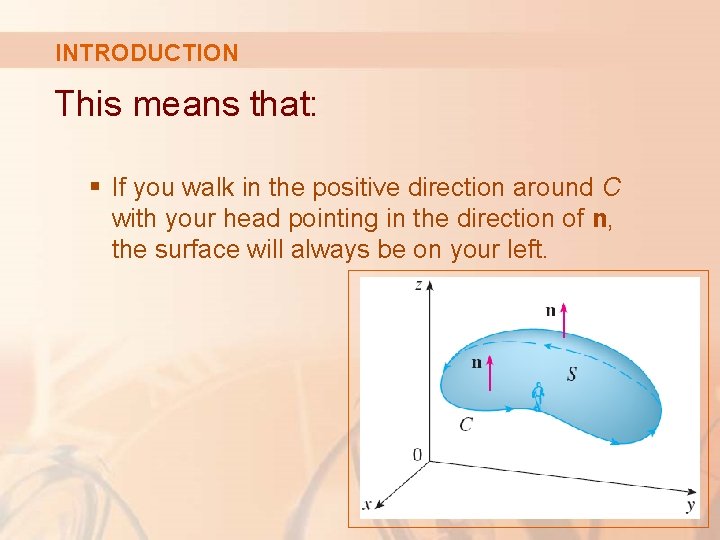
INTRODUCTION This means that: § If you walk in the positive direction around C with your head pointing in the direction of n, the surface will always be on your left.

STOKES’ THEOREM Let: § S be an oriented piecewise-smooth surface bounded by a simple, closed, piecewise-smooth boundary curve C with positive orientation. § F be a vector field whose components have continuous partial derivatives on an open region in that contains S. Then,

STOKES’ THEOREM The theorem is named after the Irish mathematical physicist Sir George Stokes (1819– 1903). § What we call Stokes’ Theorem was actually discovered by the Scottish physicist Sir William Thomson (1824– 1907, known as Lord Kelvin). § Stokes learned of it in a letter from Thomson in 1850.

STOKES’ THEOREM Thus, Stokes’ Theorem says: § The line integral around the boundary curve of S of the tangential component of F is equal to the surface integral of the normal component of the curl of F.

STOKES’ THEOREM Equation 1 The positively oriented boundary curve of the oriented surface S is often written as ∂S. So, theorem can be expressed as:

STOKES’ THEOREM, GREEN’S THEOREM, & FTC There is an analogy among Stokes’ Theorem, Green’s Theorem, and the Fundamental Theorem of Calculus (FTC). § As before, there is an integral involving derivatives on the left side of Equation 1 (recall that curl F is a sort of derivative of F). § The right side involves the values of F only on the boundary of S.

STOKES’ THEOREM, GREEN’S THEOREM, & FTC In fact, consider the special case where the surface S: § Is flat. § Lies in the xy-plane with upward orientation.

STOKES’ THEOREM, GREEN’S THEOREM, & FTC Then, § The unit normal is k. § The surface integral becomes a double integral. § Stokes’ Theorem becomes:

STOKES’ THEOREM, GREEN’S THEOREM, & FTC This is precisely the vector form of Green’s Theorem given in Equation 12 in Section 16. 5 § Thus, we see that Green’s Theorem is really a special case of Stokes’ Theorem.

STOKES’ THEOREM Stokes’ Theorem is too difficult for us to prove in its full generality. Still, we can give a proof when: § S is a graph. § F, S, and C are well behaved.

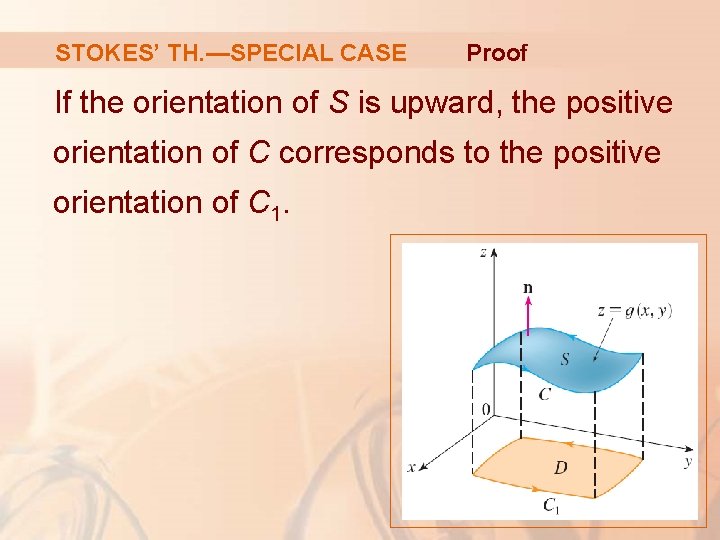
STOKES’ TH. —SPECIAL CASE Proof We assume that the equation of S is: z = g(x, y), (x, y) D where: § g has continuous second-order partial derivatives. § D is a simple plane region whose boundary curve C 1 corresponds to C.

STOKES’ TH. —SPECIAL CASE Proof If the orientation of S is upward, the positive orientation of C corresponds to the positive orientation of C 1.

STOKES’ TH. —SPECIAL CASE Proof We are also given that: F=Pi+Qj+Rk where the partial derivatives of P, Q, and R are continuous.

STOKES’ TH. —SPECIAL CASE Proof S is a graph of a function. Thus, we can apply Formula 10 in Section 16. 7 with F replaced by curl F.

STOKES’ TH. —SPECIAL CASE Proof—Equation 2 The result is: where the partial derivatives of P, Q, and R are evaluated at (x, y, g(x, y)).

STOKES’ TH. —SPECIAL CASE Proof Suppose x = x(t) y = y(t) a≤t≤b is a parametric representation of C 1. § Then, a parametric representation of C is: x = x(t) y = y(t) z = g(x(t), y(t)) a ≤ t ≤ b

STOKES’ TH. —SPECIAL CASE Proof This allows us, with the aid of the Chain Rule, to evaluate the line integral as follows:

STOKES’ TH. —SPECIAL CASE Proof § We have used Green’s Theorem in the last step.

STOKES’ TH. —SPECIAL CASE Proof Next, we use the Chain Rule again, remembering that: § P, Q, and R are functions of x, y, and z. § z is itself a function of x and y.

STOKES’ TH. —SPECIAL CASE Thus, we get: Proof

STOKES’ TH. —SPECIAL CASE Proof Four terms in that double integral cancel. The remaining six can be arranged to coincide with the right side of Equation 2. § Hence,

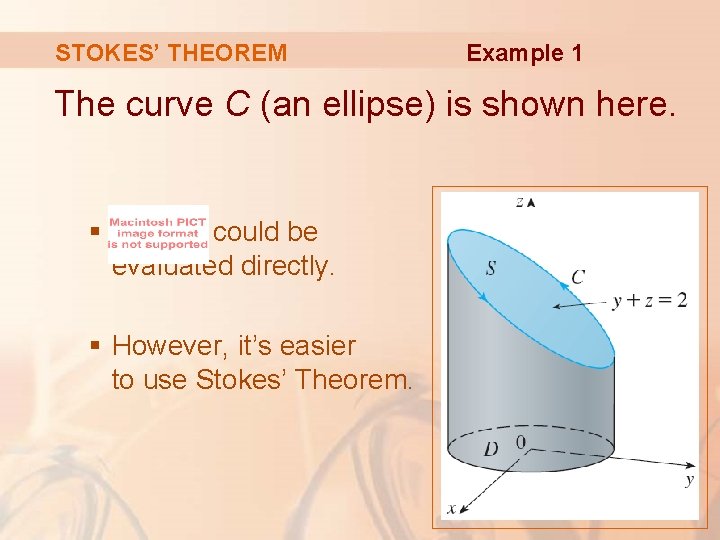
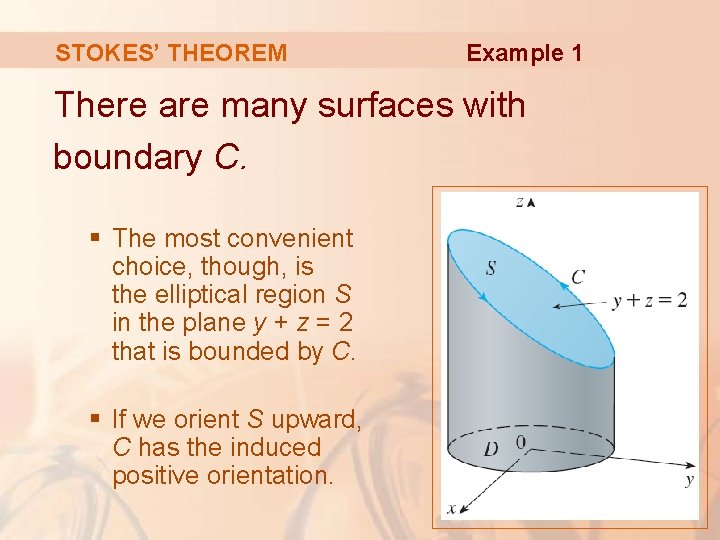
STOKES’ THEOREM Example 1 Evaluate where: § F(x, y, z) = –y 2 i + x j + z 2 k § C is the curve of intersection of the plane y + z = 2 and the cylinder x 2 + y 2 = 1. (Orient C to be counterclockwise when viewed from above. )

STOKES’ THEOREM Example 1 The curve C (an ellipse) is shown here. § could be evaluated directly. § However, it’s easier to use Stokes’ Theorem.

STOKES’ THEOREM We first compute: Example 1

STOKES’ THEOREM Example 1 There are many surfaces with boundary C. § The most convenient choice, though, is the elliptical region S in the plane y + z = 2 that is bounded by C. § If we orient S upward, C has the induced positive orientation.

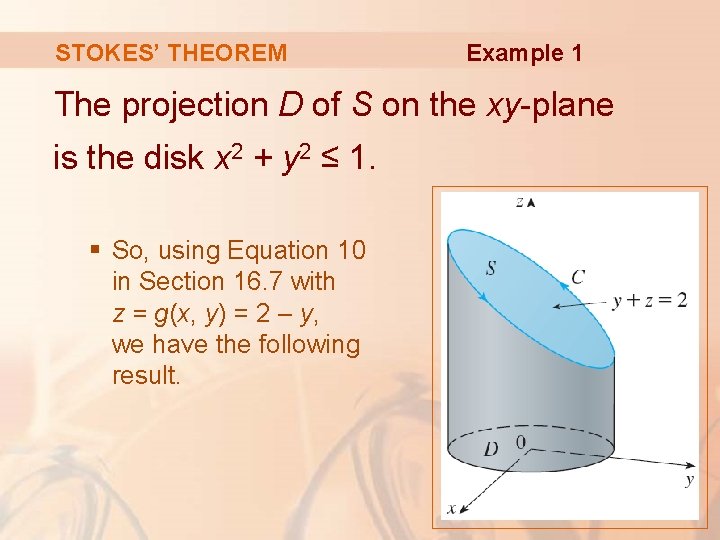
STOKES’ THEOREM Example 1 The projection D of S on the xy-plane is the disk x 2 + y 2 ≤ 1. § So, using Equation 10 in Section 16. 7 with z = g(x, y) = 2 – y, we have the following result.

STOKES’ THEOREM Example 1

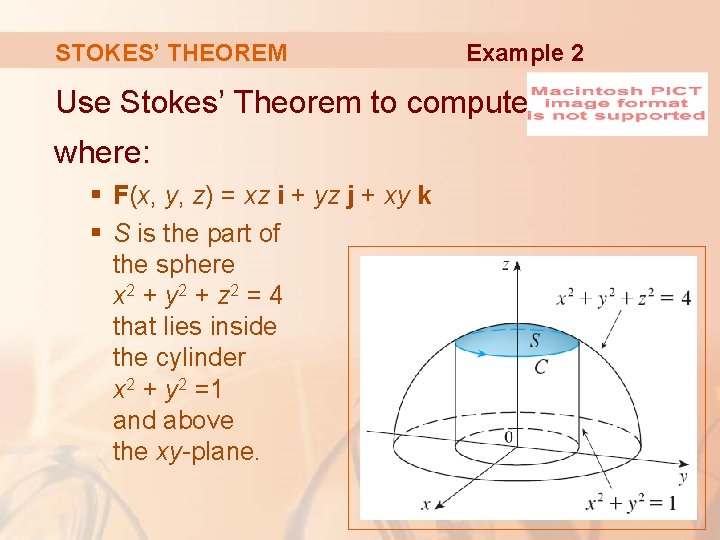
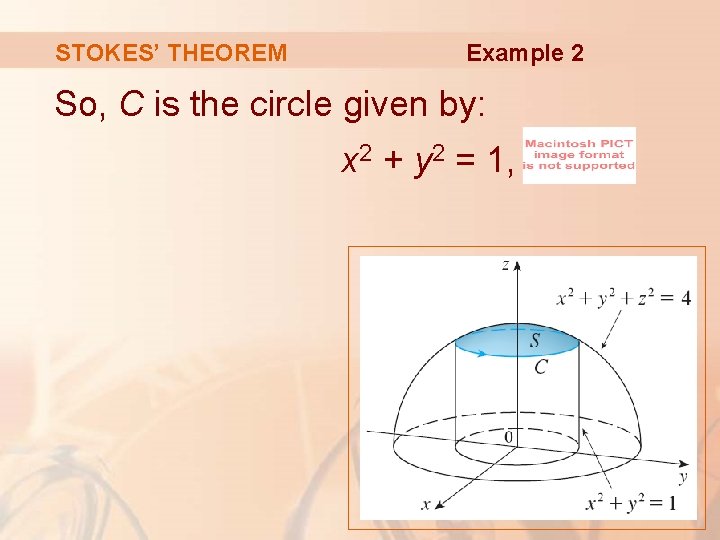
STOKES’ THEOREM Example 2 Use Stokes’ Theorem to compute where: § F(x, y, z) = xz i + yz j + xy k § S is the part of the sphere x 2 + y 2 + z 2 = 4 that lies inside the cylinder x 2 + y 2 =1 and above the xy-plane.

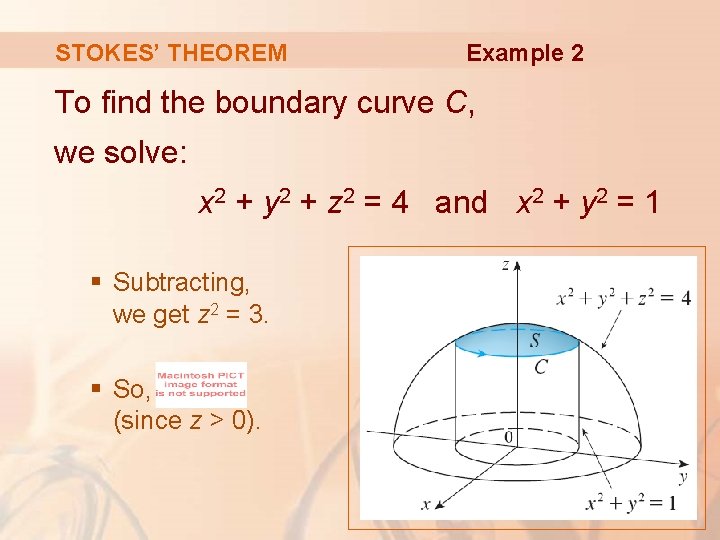
STOKES’ THEOREM Example 2 To find the boundary curve C, we solve: x 2 + y 2 + z 2 = 4 and x 2 + y 2 = 1 § Subtracting, we get z 2 = 3. § So, (since z > 0).

STOKES’ THEOREM Example 2 So, C is the circle given by: x 2 + y 2 = 1,

STOKES’ THEOREM Example 2 A vector equation of C is: r(t) = cos t i + sin t j + k § Therefore, r’(t) = –sin t i + cos t j Also, we have: 0 ≤ t ≤ 2π

STOKES’ THEOREM Thus, by Stokes’ Theorem, Example 2

STOKES’ THEOREM Note that, in Example 2, we computed a surface integral simply by knowing the values of F on the boundary curve C. This means that: § If we have another oriented surface with the same boundary curve C, we get exactly the same value for the surface integral!

STOKES’ THEOREM Equation 3 In general, if S 1 and S 2 are oriented surfaces with the same oriented boundary curve C and both satisfy the hypotheses of Stokes’ Theorem, then § This fact is useful when it is difficult to integrate over one surface but easy to integrate over the other.

CURL VECTOR We now use Stokes’ Theorem to throw some light on the meaning of the curl vector. § Suppose that C is an oriented closed curve and v represents the velocity field in fluid flow.

CURL VECTOR Consider the line integral and recall that v ∙ T is the component of v in the direction of the unit tangent vector T. § This means that the closer the direction of v is to the direction of T, the larger the value of v ∙ T.

CIRCULATION Thus, is a measure of the tendency of the fluid to move around C. § It is called the circulation of v around C.

CURL VECTOR Now, let: P 0(x 0, y 0, z 0) be a point in the fluid. Sa be a small disk with radius a and center P 0. § Then, (curl F)(P) ≈ (curl F)(P 0) for all points P on Sa because curl F is continuous.

CURL VECTOR Thus, by Stokes’ Theorem, we get the following approximation to the circulation around the boundary circle Ca:

CURL VECTOR Equation 4 The approximation becomes better as a → 0. Thus, we have:

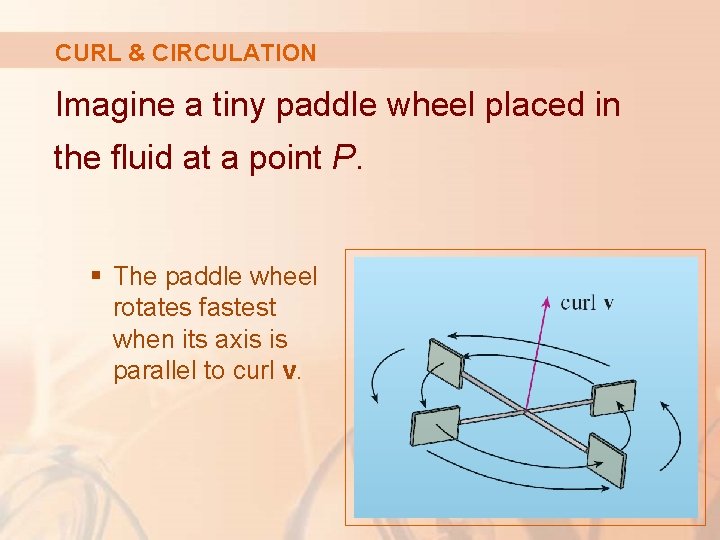
CURL & CIRCULATION Equation 4 gives the relationship between the curl and the circulation. § It shows that curl v ∙ n is a measure of the rotating effect of the fluid about the axis n. § The curling effect is greatest about the axis parallel to curl v.

CURL & CIRCULATION Imagine a tiny paddle wheel placed in the fluid at a point P. § The paddle wheel rotates fastest when its axis is parallel to curl v.

CLOSED CURVES Finally, we mention that Stokes’ Theorem can be used to prove Theorem 4 in Section 16. 5: § If curl F = 0 on all of , then F is conservative.

CLOSED CURVES From Theorems 3 and 4 in Section 16. 3, we know that F is conservative if for every closed path C. § Given C, suppose we can find an orientable surface S whose boundary is C. § This can be done, but the proof requires advanced techniques.

CLOSED CURVES Then, Stokes’ Theorem gives: § A curve that is not simple can be broken into a number of simple curves. § The integrals around these curves are all 0.

CLOSED CURVES Adding these integrals, we obtain: for any closed curve C.