16 Angular Momentum 1 Angular Momentum Operator 2

16. Angular Momentum 1. Angular Momentum Operator 2. Angular Momentum Coupling 3. Spherical Tensors 4. Vector Spherical Harmonics

Principles of Quantum Mechanics State of a particle is described by a wave function (r, t). Probability of finding the particle at time t within volume d 3 r around r is Dynamics of particle is given by the time-dependent Schrodinger eq. Hamiltonian SI units: Stationary states satisfy the time-independent Schrodinger eq. with

Let be an eigenstate of A with eigenvalue a, i. e. Measurement of A on a particle in state will give a and the particle will remain in afterwards. Operators A & B have a set of simultaneous eigenfunctions. A stationary state is specified by the eigenvalues of the maximal set of operators commuting with H. Measurement of A on a particle in state will give one of the eigenvalues a of A with probability and the particle will be in a afterwards. uncertainty principle

1. Angular Momentum Operator Quantization rule : Kinetic energy of a particle of mass : Angular momentum : Rotational energy : angular part of T

Ex. 3. 10. 32 with

Central Force Cartesian commonents Ex. 3. 10. 31 : eigenstates of H can be labeled by eigenvalues of L 2 & Lz , i. e. , by l, m. Ex. 3. 10. 29 -30

Ladder Operators Ladder operators Let lm be a normalized eigenfunction of L 2 & Lz such that i. e. is an eigenfunction of Lz with eigenvalue ( m 1) . L are Raising operators Lowering

is an eigenfunction of L 2 with eigenvalue l 2. i. e. lm normalized a real Ylm thus generated agrees with the Condon-Shortley phase convention.

For m 0 : m = 1 0 0 Multiplicity = 2 l+1

Example 16. 1. 1. Spherical Harmonics Ladder for l = 0, 1, 2, …

Spinors Intrinsic angular momenta (spin) S of fermions have s = half integers. E. g. , for electrons Eigenspace is 2 -D with basis Or in matrix form : spinors S are proportional to the Pauli matrices.

Example 16. 1. 2. Spinor Ladder Fundamental relations that define an angular momentum, i. e. , can be verified by direct matrix calculation. Mathematica Spinors:

Summary, Angular Momentum Formulas General angular momentum : Eigenstates JM : J = 0, 1/2, 1, 3/2, 2, … M = J, …, J

2. Angular Momentum Coupling Let Implicit summation applies only to the k, l, n indices

Example 16. 2. 1. Commutation Rules for J Components e. g.

Maximal commuting set of operators : or eigen states : Adding (coupling) Solution always exists & unique since means finding is complete.

Vector Model Total number of states : i. e. Mathematica Triangle rule

Clebsch-Gordan Coefficients For a given j 1 & j 2 , we can write the basis as & Both set of basis are complete : Clebsch-Gordan Coefficients (CGC) Condon-Shortley phase convention

Ladder Operation Construction Repeated applications of J then give the rest of the multiplet Orthonormality :

Clebsch-Gordan Coefficients Full notations : real Only terms with no negative factorials are included in sum.

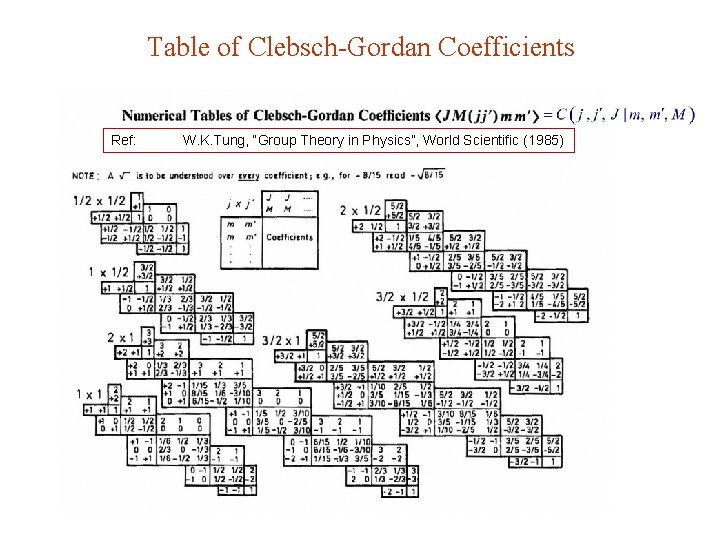
Table of Clebsch-Gordan Coefficients Ref: W. K. Tung, “Group Theory in Physics”, World Scientific (1985)

Wigner 3 j - Symbols Advantage : more symmetric

Table 16. 1 Wigner 3 j-Symbols Mathematica

Example 16. 2. 2. Two Spinors

Simpler Notations

Example 16. 2. 3. Coupling of p & d Electrons Simpler notations : where l 0 1 2 3 s p d f Mathematica

Mathematica