16 548 Coding and Information Theory Lecture 15

16. 548 Coding and Information Theory Lecture 15: Space Time Coding and MIMO: 1

Credits 2

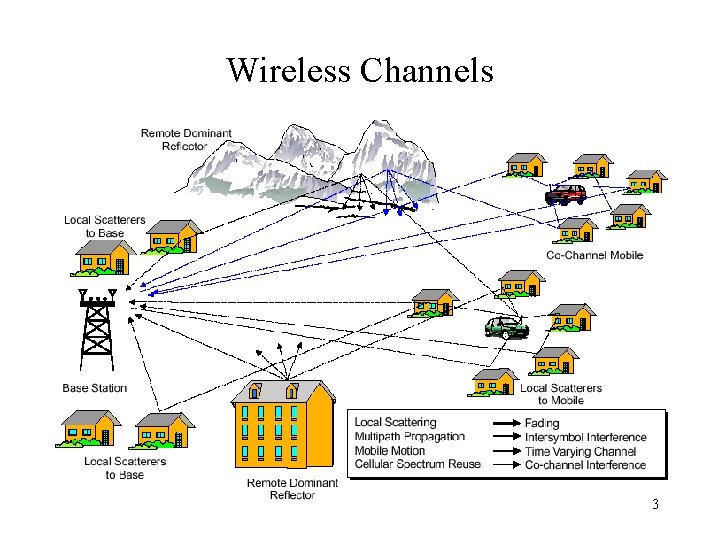
Wireless Channels 3

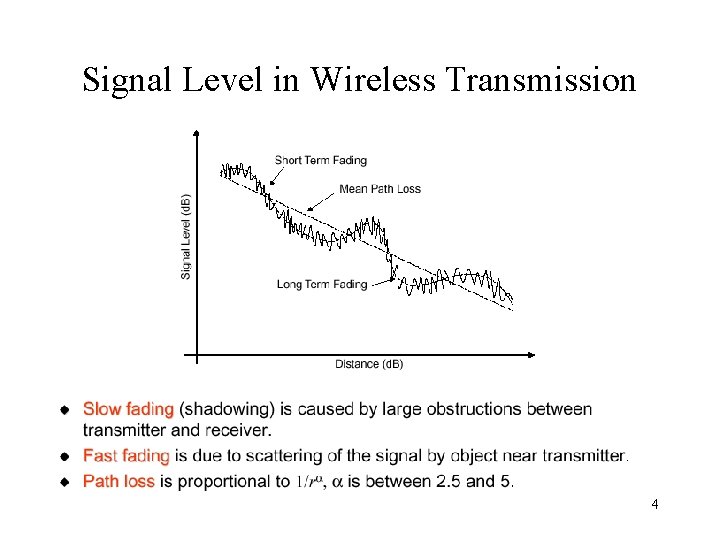
Signal Level in Wireless Transmission 4

Classification of Wireless Channels 5

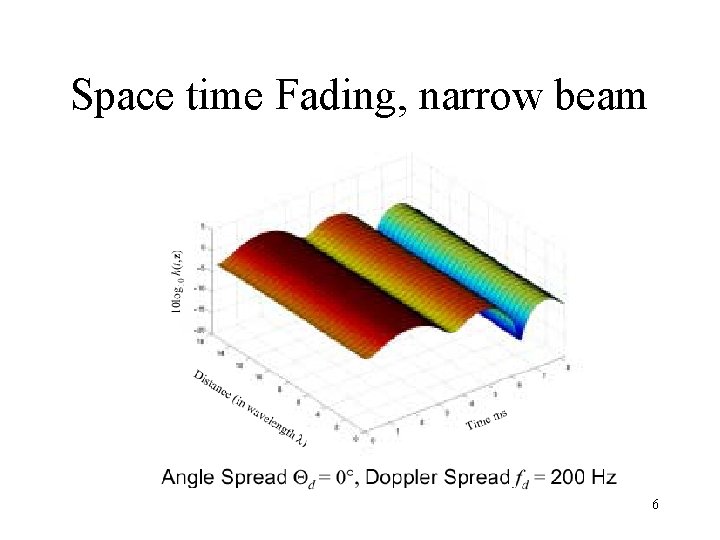
Space time Fading, narrow beam 6

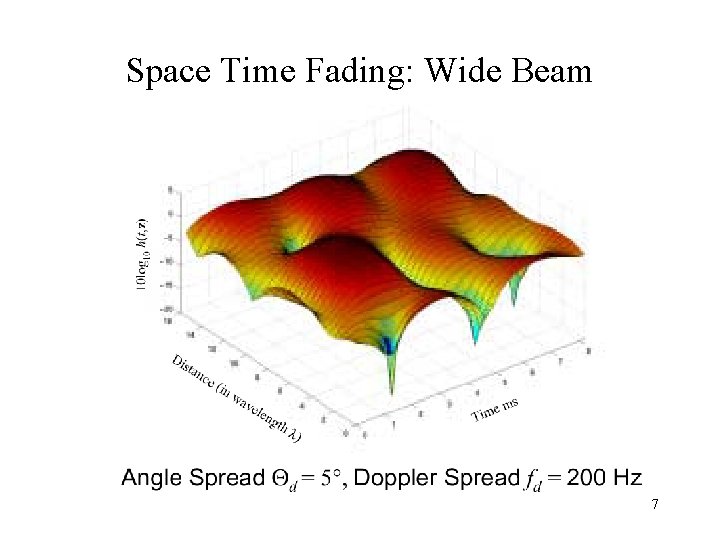
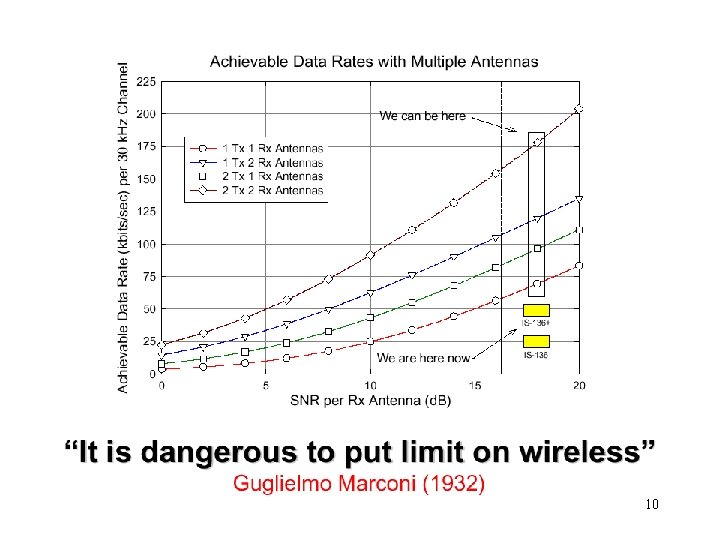
Space Time Fading: Wide Beam 7

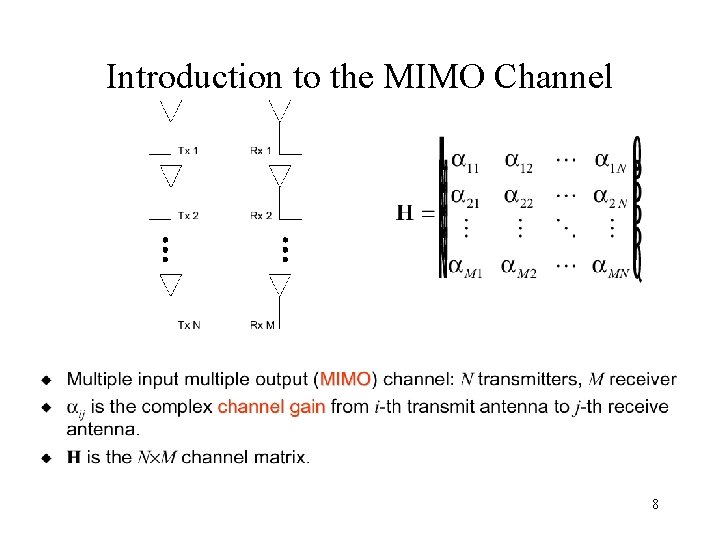
Introduction to the MIMO Channel 8

Capacity of MIMO Channels 9

10

Single Input- Single Output systems (SISO) g y(t) x(t): transmitted signal y(t): received signal g(t): channel transfer function n(t): noise (AWGN, 2) x(t) y(t) = g • x(t) + n(t) Signal to noise ratio : Capacity : C = log 2(1+ ) 11

Single Input- Multiple Output (SIMO Multiple Input- Single Output (MISO • Principle of diversity systems (transmitter/ receiver) • +: Higher average signal to noise ratio Robustness • - : Process of diminishing return Benefit reduces in the presence of correlation • Maximal ratio combining > Equal gain combining > Selection combining 12

Idea behind diversity systems • Use more than one copy of the same signal • If one copy is in a fade, it is unlikely that all the others will be too. 1 N • C 1 x. N>C 1 x 1 • C 1 x. N more robust than C 1 x 1 13

Background of Diversity Techniques • Variety of Diversity techniques are proposed to combat Time-Varying Multipath fading channel in wireless communication – Time Diversity – Frequency Diversity – Space Diversity (mostly multiple receive antennas) • Main intuitions of Diversity: – Probability of all the signals suffer fading is less then probability of single signal suffer fading – Provide the receiver a multiple versions of the same Tx signals over independent channels • Time Diversity – Use different time slots separated by an interval longer than the coherence time of the channel. – Example: Channel coding + interleaving – Short Coming: Introduce large delays when the channel is in slow fading 14

Diversity Techniques • Improve the performance in a fading environment – Space Diversity • Spacing is important! (coherent distance) – Polarization Diversity • Using antennas with different polarizations for reception/transmission. – Frequency Diversity • RAKE receiver, OFDM, equalization, and etc. • Not effective over frequency-flat channel. – Time Diversity • Using channel coding and interleaving. • Not effective over slow fading channels. 15

RX Diversity in Wireless 16

Receive Diversity 17

Selection and Switch Diversity 18

Linear Diversity 19

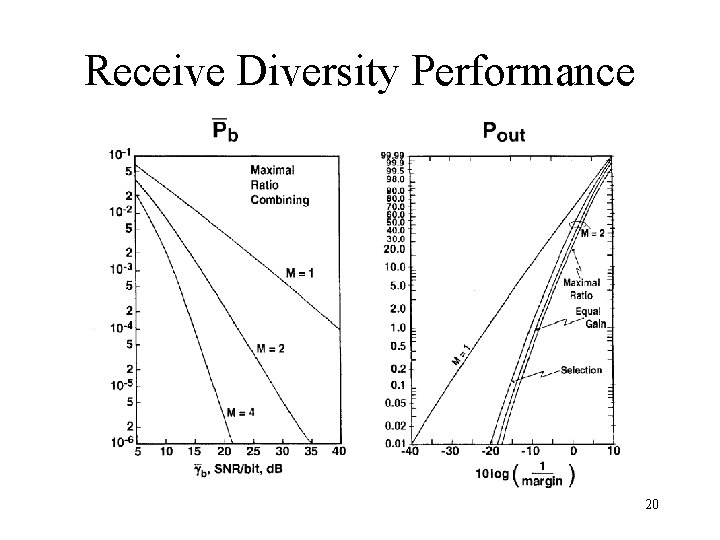
Receive Diversity Performance 20

Transmit Diversity 21

Transmit Diversity with Feedback 22

TX diversity with frequency weighting 23

TX Diversity with antenna hopping 24

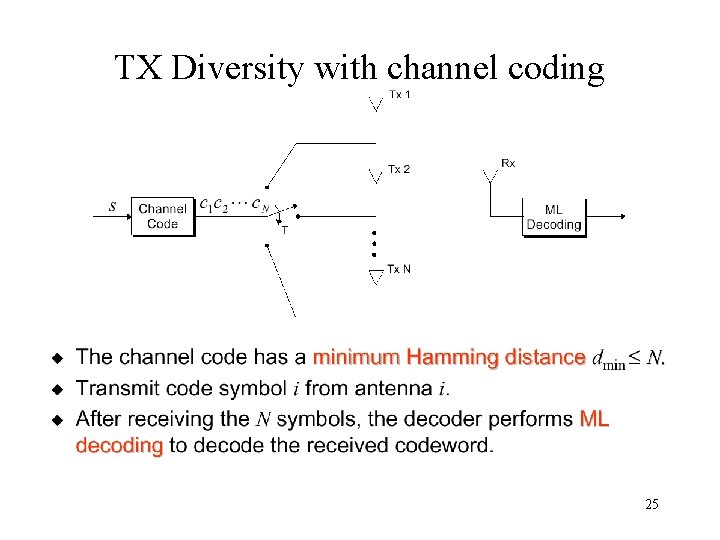
TX Diversity with channel coding 25

Transmit diversity via delay diversity 26

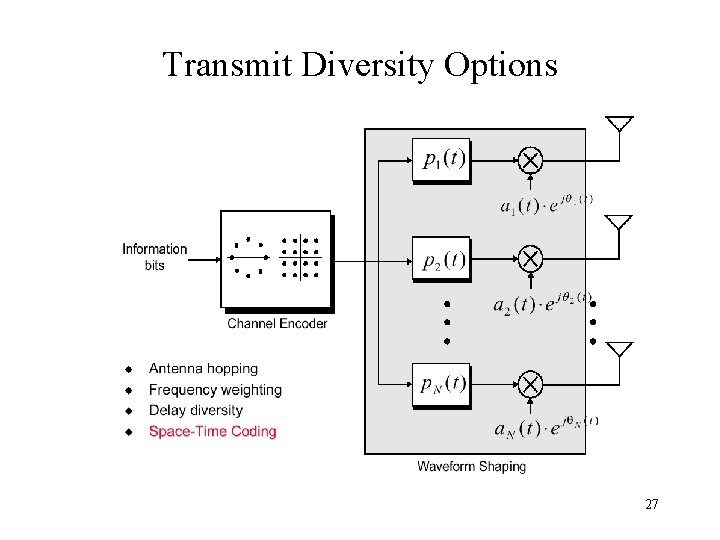
Transmit Diversity Options 27

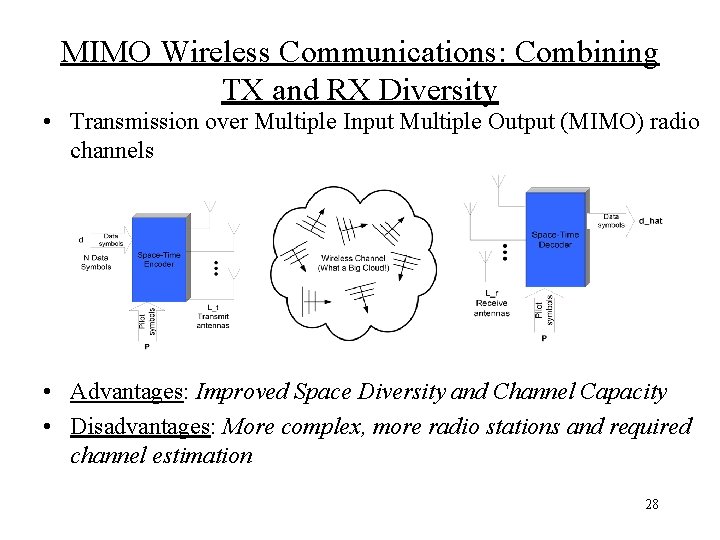
MIMO Wireless Communications: Combining TX and RX Diversity • Transmission over Multiple Input Multiple Output (MIMO) radio channels • Advantages: Improved Space Diversity and Channel Capacity • Disadvantages: More complex, more radio stations and required channel estimation 28

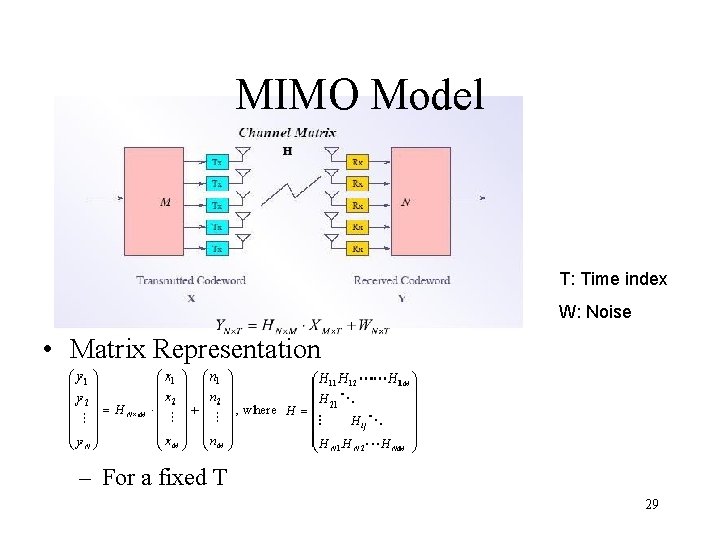
MIMO Model T: Time index W: Noise • Matrix Representation – For a fixed T 29

Part II: Space Time Coding 30

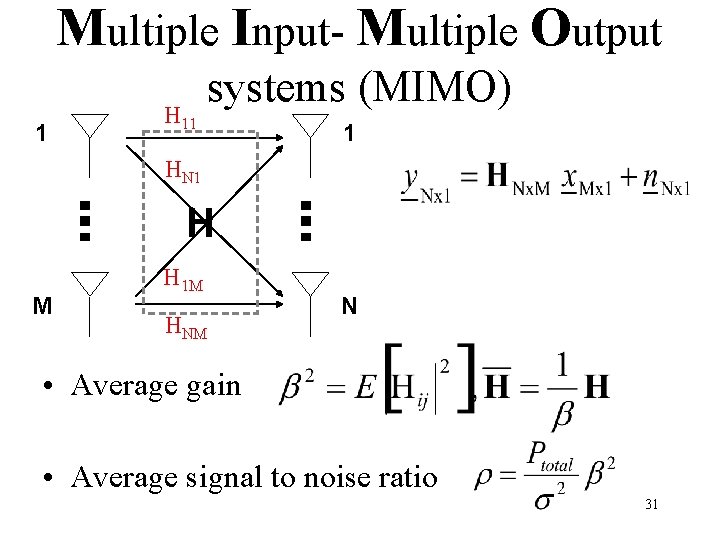
Multiple Input- Multiple Output 1 H 11 systems (MIMO) 1 HN 1 H M H 1 M HNM N • Average gain • Average signal to noise ratio 31

Shannon capacity K= rank(H): what is its range of values? Parameters that affect the system capacity • Signal to noise ratio • Distribution of eigenvalues (u) of H 32

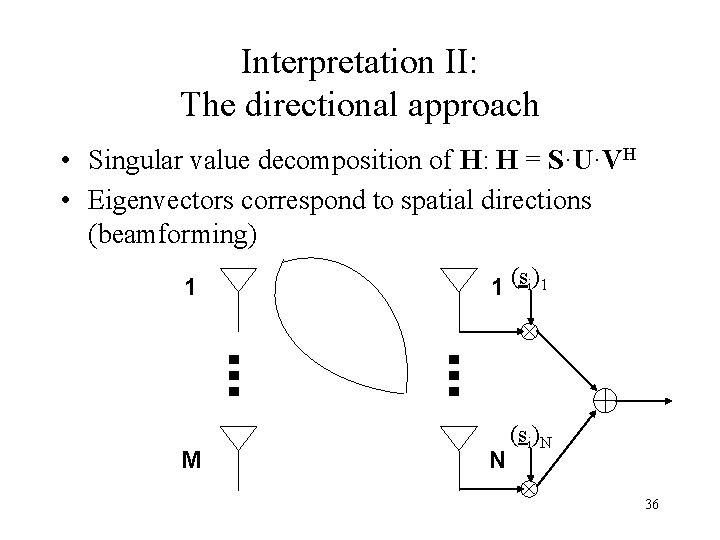
Interpretation I: The parallel channels approach • “Proof” of capacity formula • Singular value decomposition of H: H = S·U·VH • S, V: unitary matrices (VHV=I, SSH =I) U : = diag(uk), uk singular values of H • V/ S: input/output eigenvectors of H • Any input along vi will be multiplied by ui and will appear as an output along si 33

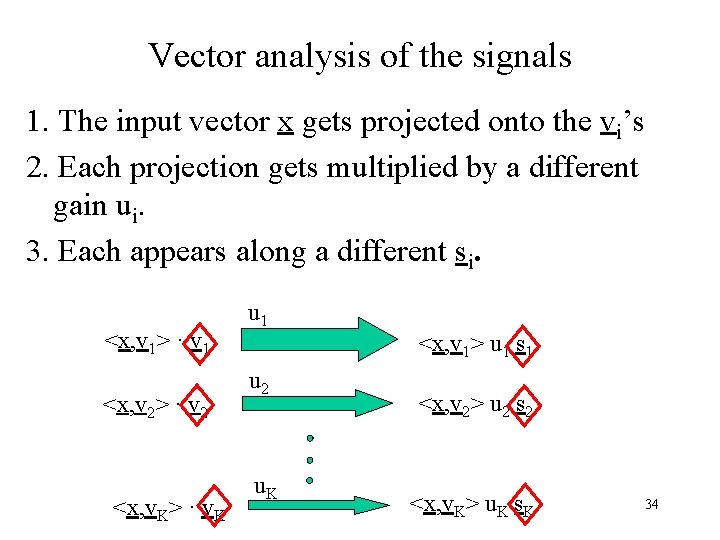
Vector analysis of the signals 1. The input vector x gets projected onto the vi’s 2. Each projection gets multiplied by a different gain ui. 3. Each appears along a different si. <x, v 1> · v 1 <x, v 2> · v 2 <x, v. K> · v. K u 1 <x, v 1> u 1 s 1 u 2 u. K <x, v 2> u 2 s 2 <x, v. K> u. K s. K 34

Capacity = sum of capacities • The channel has been decomposed into K parallel subchannels • Total capacity = sum of the subchannel capacities • All transmitters send the same power: Ex=Ek 35

Interpretation II: The directional approach • Singular value decomposition of H: H = S·U·VH • Eigenvectors correspond to spatial directions (beamforming) 1 M 1 (si)1 N (si)N 36

Example of directional interpretation 37

38

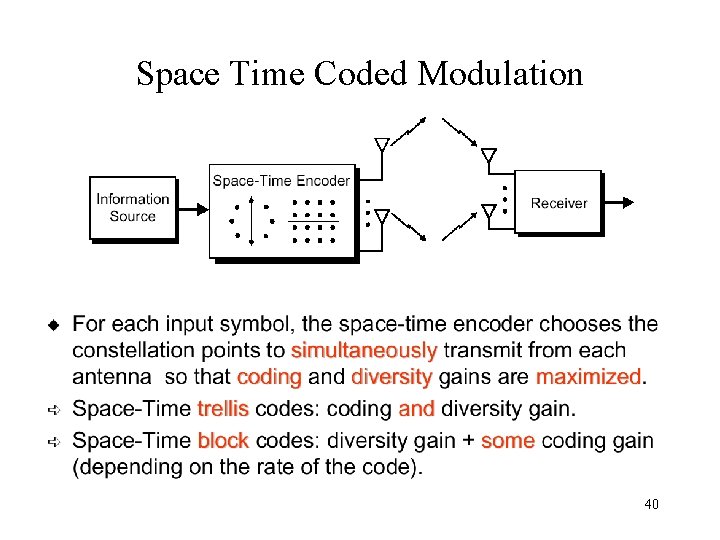
Space-Time Coding • What is Space-Time Coding? – Space diversity at antenna – Time diversity to introduce redundant data • Alamouti-Scheme – Simple yet very effective – Space diversity at transmitter end – Orthogonal block code design 39

Space Time Coded Modulation 40

Space Time Channel Model 41

42

STC Error Analysis 43

STC Error Analysis 44

45

46

STC Design Criteria 47

48

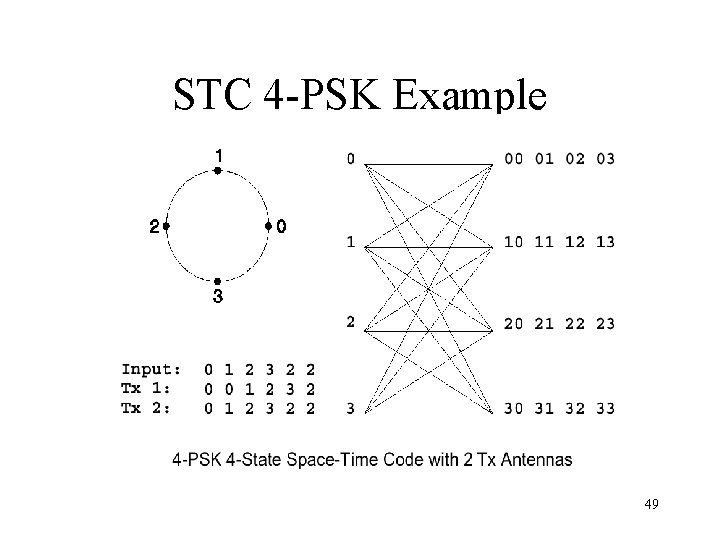
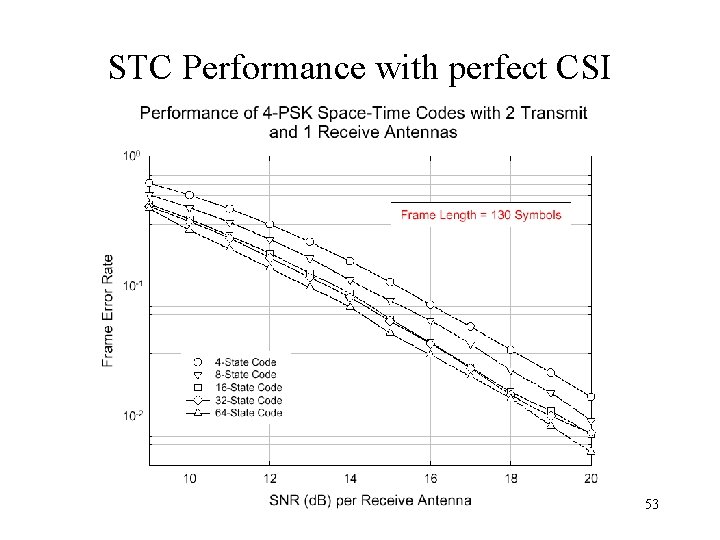
STC 4 -PSK Example 49

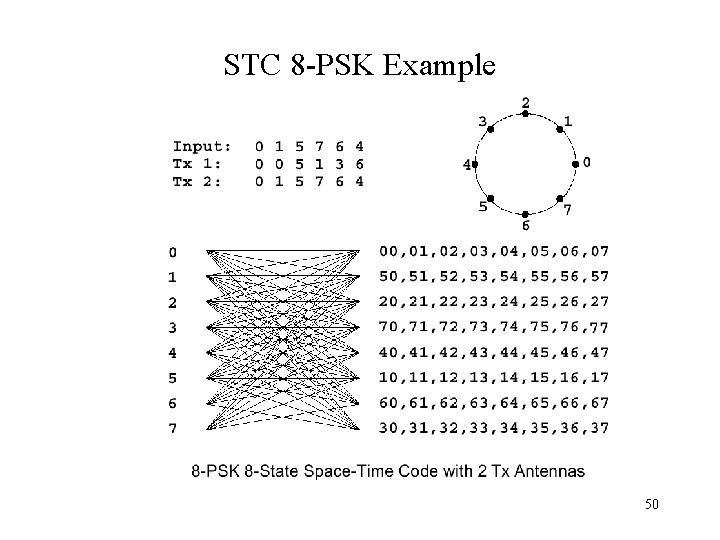
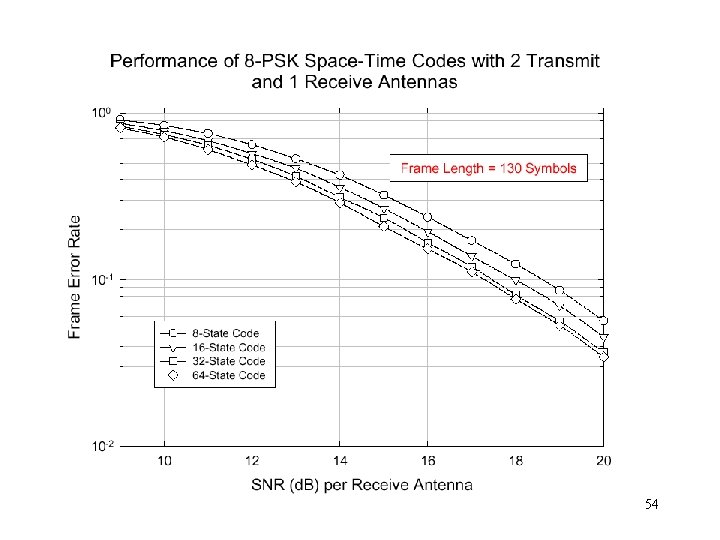
STC 8 -PSK Example 50

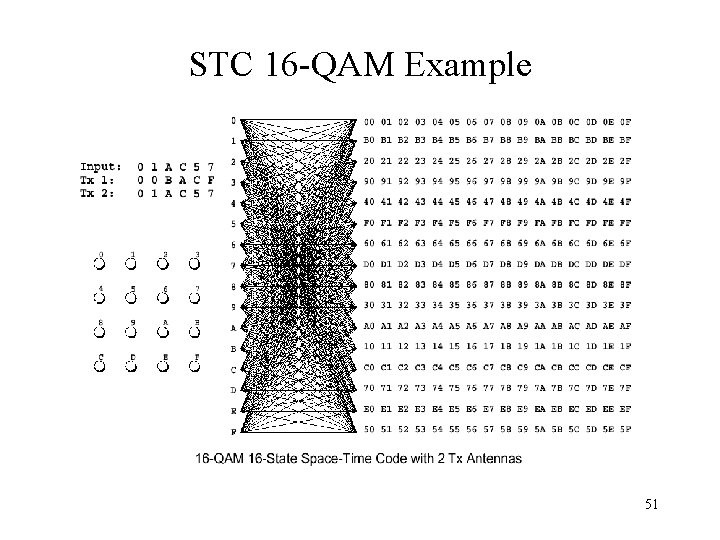
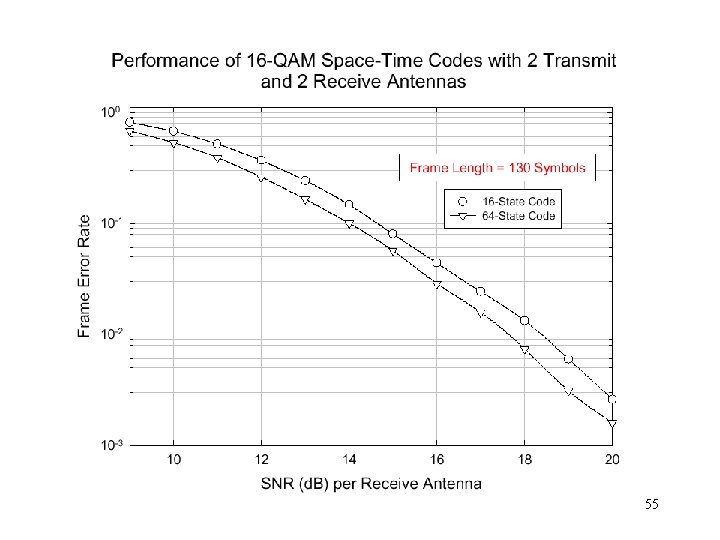
STC 16 -QAM Example 51

STC Maximum Likelihood Decoder 52

STC Performance with perfect CSI 53

54

55

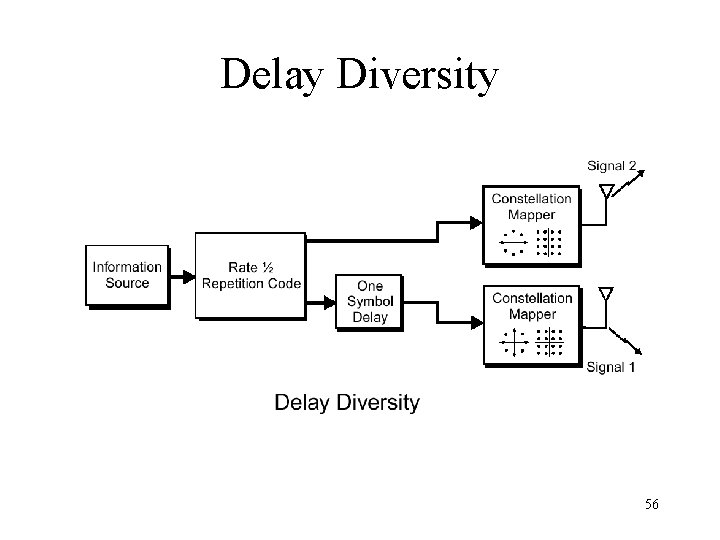
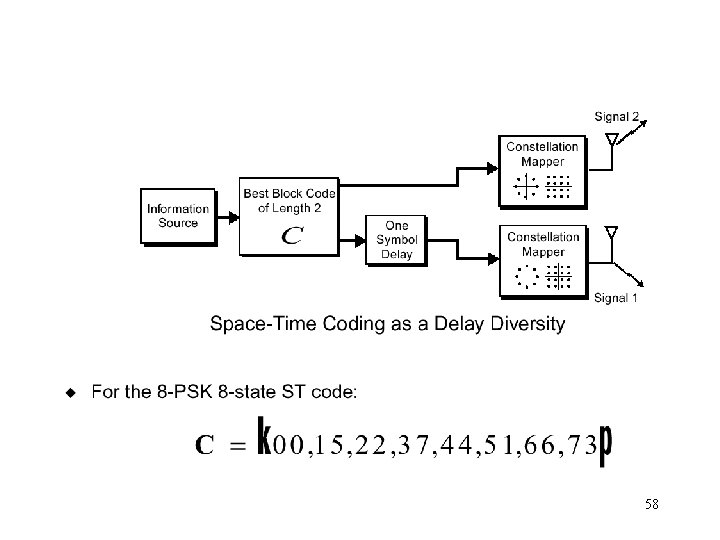
Delay Diversity 56

Delay Diversity ST code 57

58

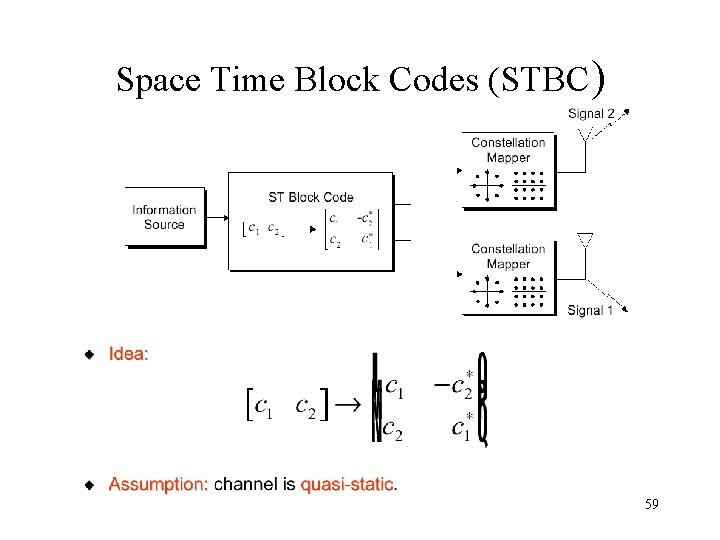
Space Time Block Codes (STBC) 59

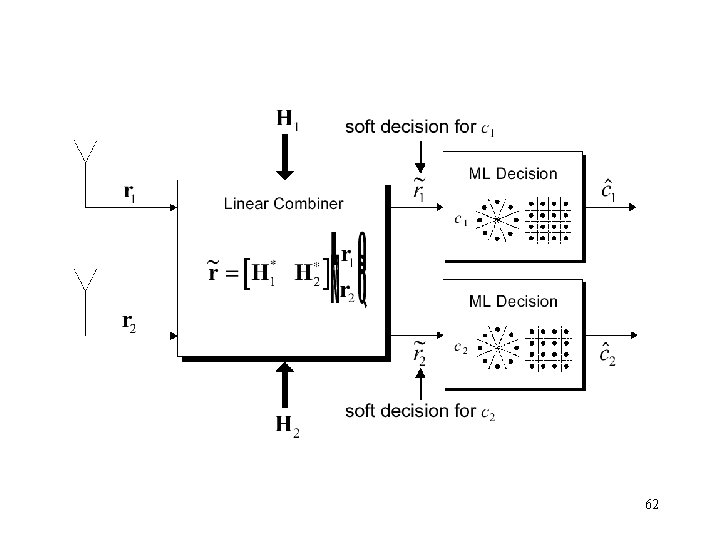
Decoding STBC 60

61

62

Block and Data Model • 1 X(N+P) block of information symbols broadcast from transmit antenna: i Si(d, t) • 1 X(N+P) block of received information symbols taken from antenna: j Rj = hji. Si(d, t) + nj • Matrix representation: 63

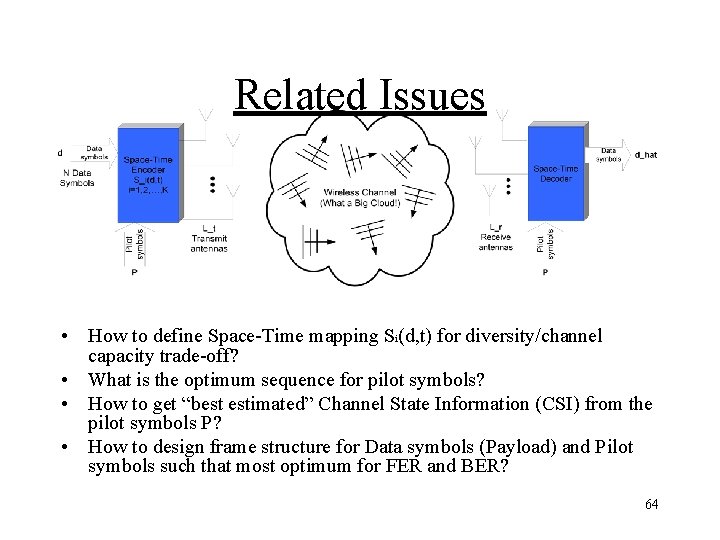
Related Issues • How to define Space-Time mapping Si(d, t) for diversity/channel capacity trade-off? • What is the optimum sequence for pilot symbols? • How to get “best estimated” Channel State Information (CSI) from the pilot symbols P? • How to design frame structure for Data symbols (Payload) and Pilot symbols such that most optimum for FER and BER? 64

Specific Example of STBC: Alamouti’s Orthogonal Code • Let’s consider two antenna i and i+1 at the transmitter side, at two consecutive time instants t and t+T: • The above Space-Time mapping defines Alamouti’s Code[1]. • A general frame design requires concatenation of blocks (each 2 X 2) of Alamouti code, 65

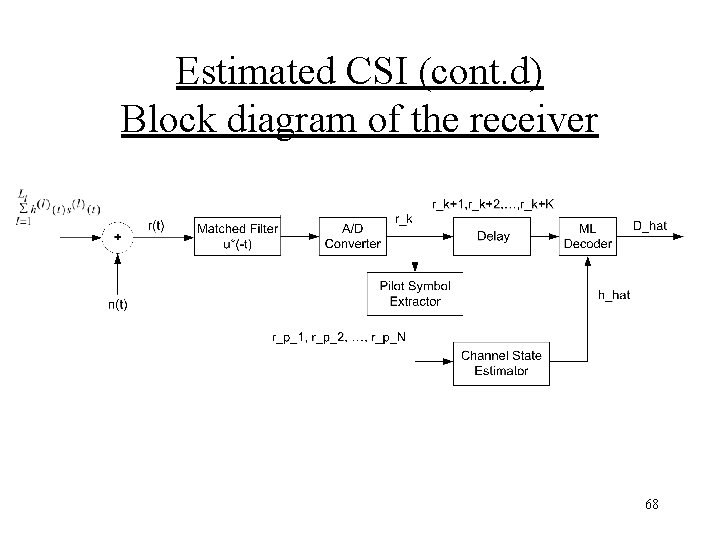
Estimated Channel State Information (CSI) • Pilot Symbol Assisted Modulation (PSAM) [3] is used to obtain estimated Channel State Information (CSI) • PSAM simply samples the channel at a rate greater than Nyquist rate, so that reconstruction is possible • Here is how it works… 66

Channel State Estimation 67

Estimated CSI (cont. d) Block diagram of the receiver 68

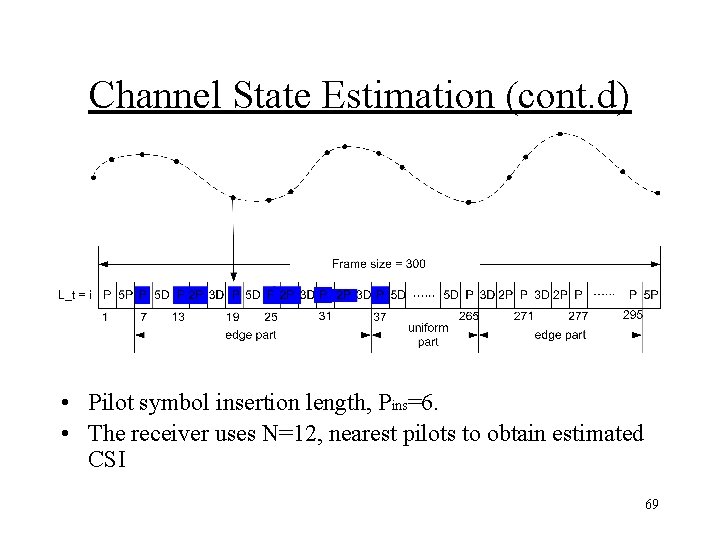
Channel State Estimation (cont. d) • Pilot symbol insertion length, Pins=6. • The receiver uses N=12, nearest pilots to obtain estimated CSI 69

Channel State Estimation Cont. d • Pilot Symbols could be think of as redundant data symbols • Pilot symbol insertion length will not change the performance much, as long as we sample faster than fading rate of the channel • If the channel is in higher fading rate, more pilots are expected to be inserted 70

Estimated CSI, Space-time PSAM frame design • The orthogonal pilot symbol (pilots chosen from QPSK constellation) matrix is, [4] • Pilot symbol insertion length, Pins=6. • The receiver uses N=12, nearest pilots to obtain estimated CSI • Data = 228, Pilots = 72 71

Channel State Estimation (cont. d) MMSE estimation • Use Wiener filtering, since it is a Minimum Mean Square Error (MMSE) estimator • All random variables involved are jointly Gaussian, MMSE estimator becomes a linear minimum mean square estimator [2]: • Wiener filter is defined as, • Note, . and 72

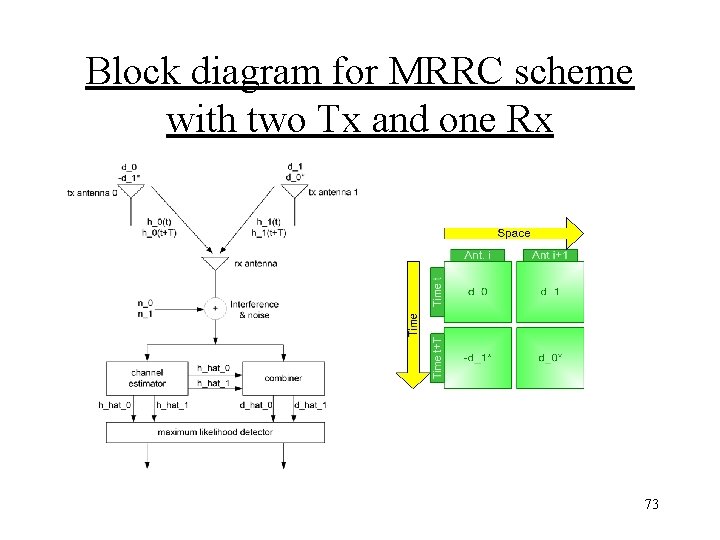
Block diagram for MRRC scheme with two Tx and one Rx 73

Block diagram for MRRC scheme with two Tx and one Rx • The received signals can then be expressed as, • The combiner shown in the above graph builds the following two estimated signal 74

Maximum Likelihood Decoding Under QPSK Constellation • Output of the combiner could be further simplified and could be expressed as follows: • For example, under QPSK constellation decision are made according to the axis. 75

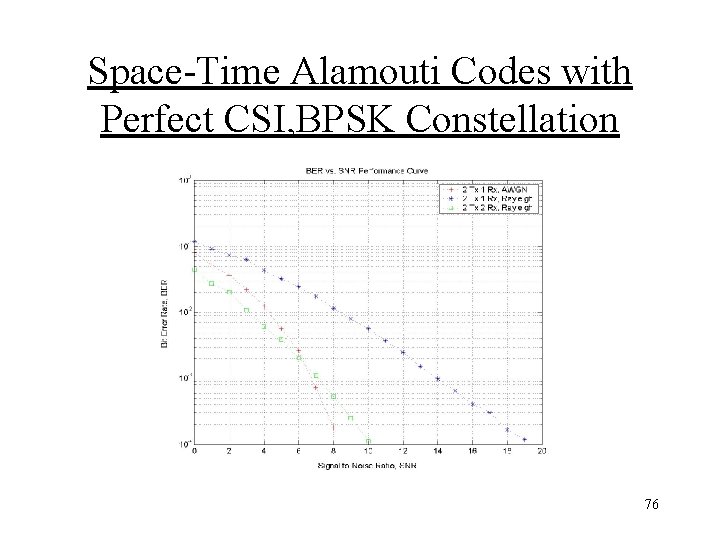
Space-Time Alamouti Codes with Perfect CSI, BPSK Constellation 76

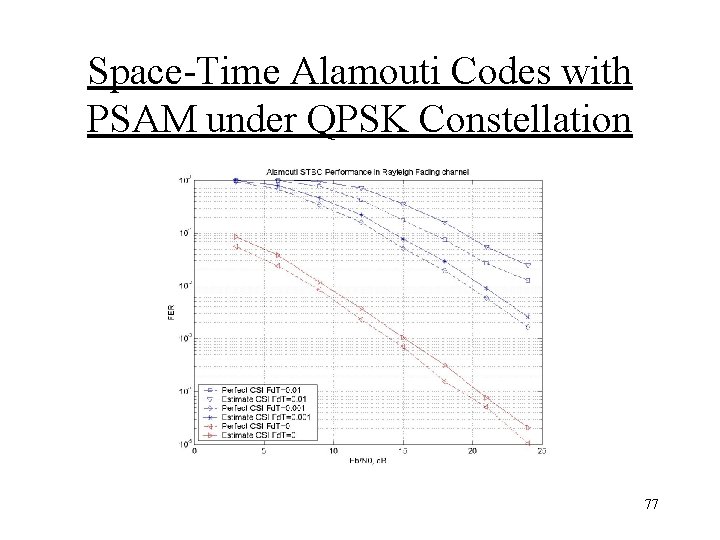
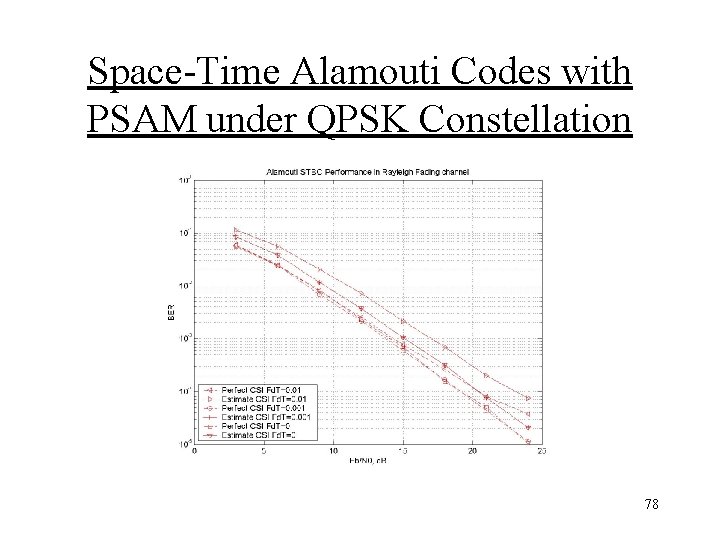
Space-Time Alamouti Codes with PSAM under QPSK Constellation 77

Space-Time Alamouti Codes with PSAM under QPSK Constellation 78

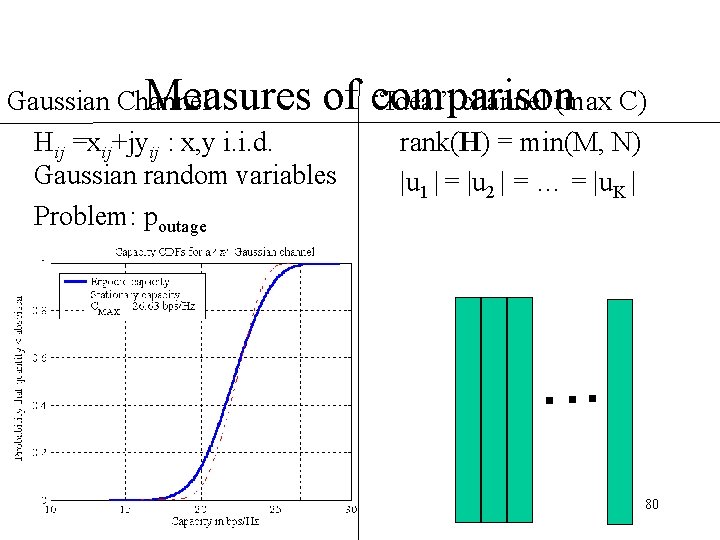
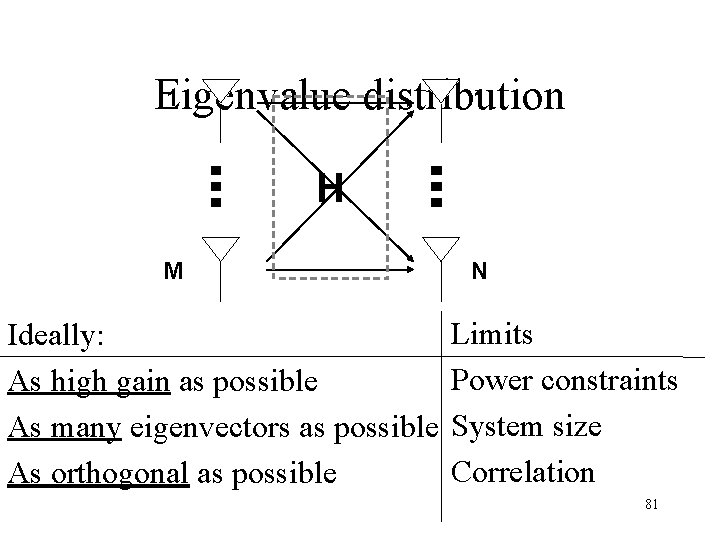
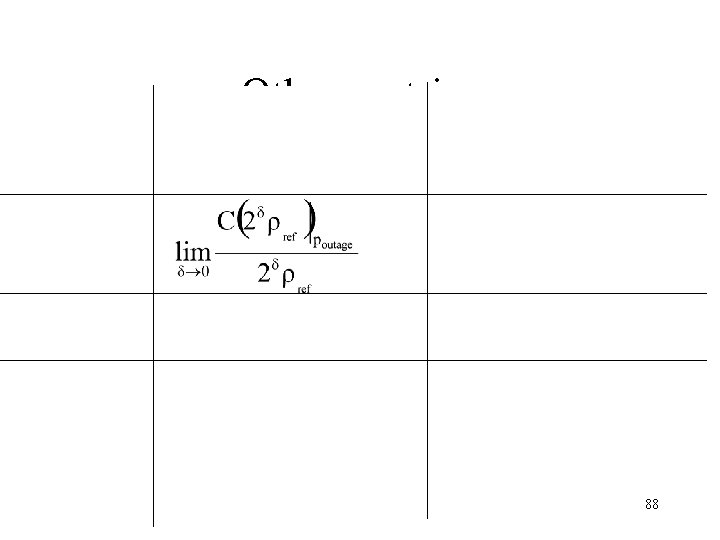
Performance metrics • Measures of comparison – Gaussian iid channel – “ideal” channel • Eigenvalue distribution • Shannon capacity – for constant SNR or – for constant transmitted power • Effective degrees of freedom(EDOF) • Condition number 79

Measures of comparison Gaussian Channel “Ideal” channel (max C) Hij =xij+jyij : x, y i. i. d. rank(H) = min(M, N) Gaussian random variables |u 1 | = |u 2 | = … = |u. K | Problem: poutage 80

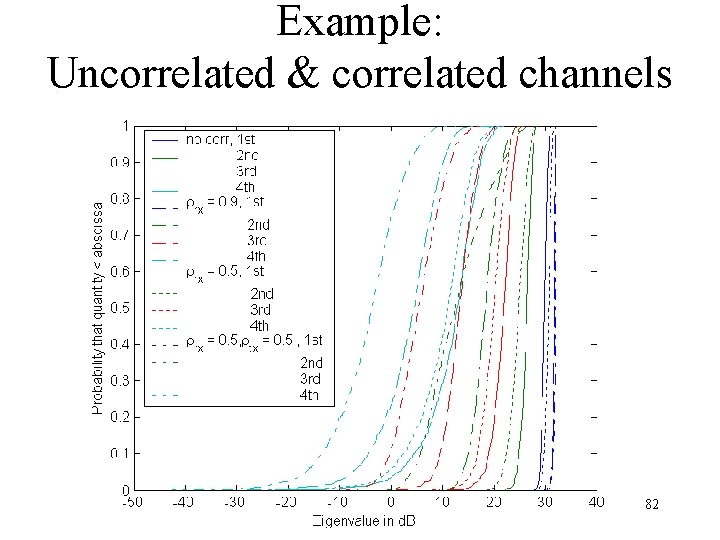
1 1 Eigenvalue distribution H M Ideally: As high gain as possible As many eigenvectors as possible As orthogonal as possible N Limits Power constraints System size Correlation 81

Example: Uncorrelated & correlated channels 82

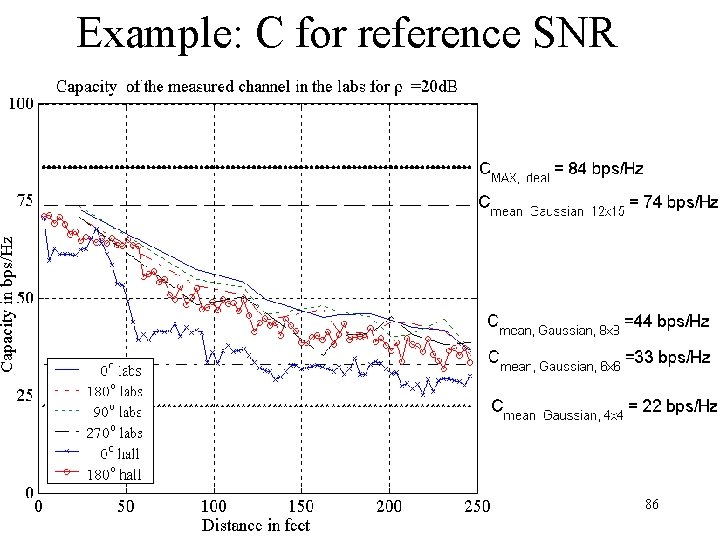
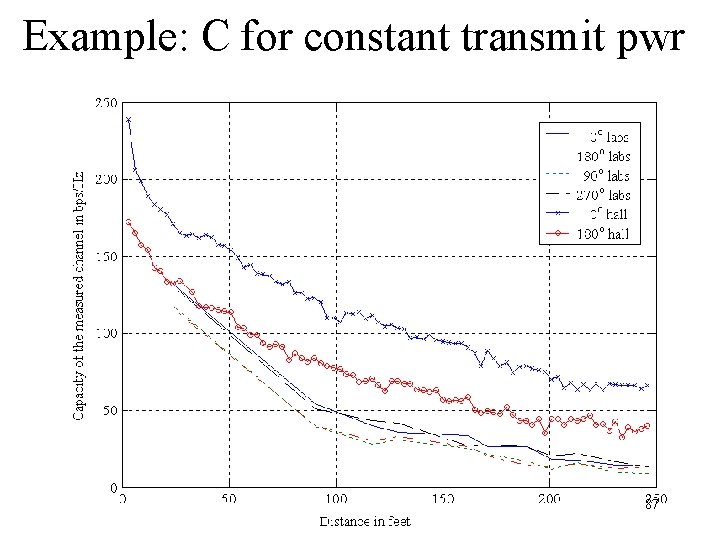
Shannon capacity • Capacity for a reference SNR (only channel info) • Capacity for constant transmitted power (channel + power roll-off info) 83

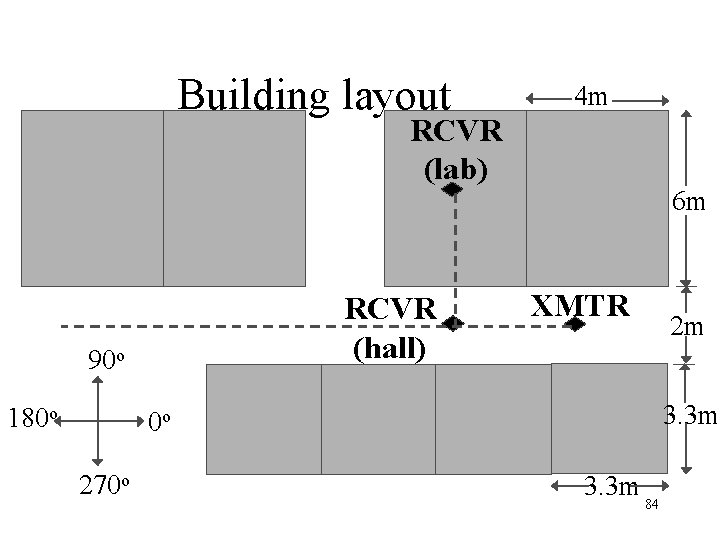
Building layout 4 m RCVR (lab) RCVR (hall) 90 o 180 o 6 m XMTR 3. 3 m 0 o 270 o 2 m 3. 3 m 84

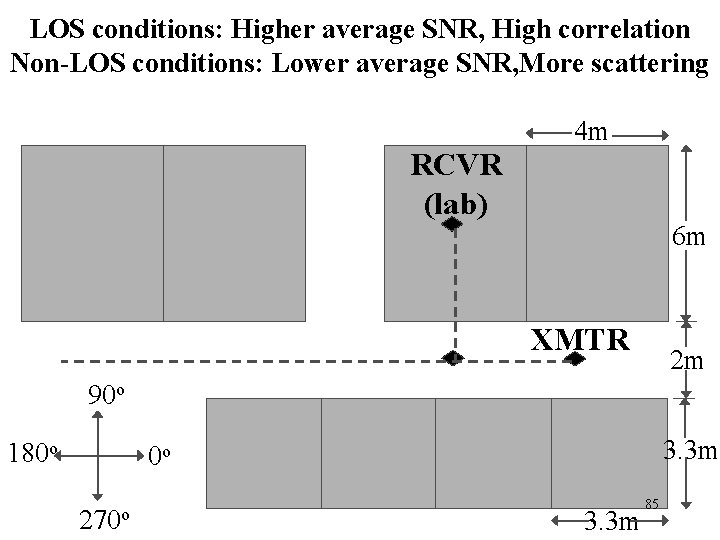
LOS conditions: Higher average SNR, High correlation Non-LOS conditions: Lower average SNR, More scattering 4 m RCVR (lab) 6 m XMTR 2 m 90 o 180 o 3. 3 m 0 o 270 o 3. 3 m 85

Example: C for reference SNR 86

Example: C for constant transmit pwr 87

Other metrics 88

From narrowband to wideband • Wideband: delay spread >> symbol time • -: Intersymbol interference +: Frequency diversity • SISO channel impulse response: SISO capacity: 89

Matrix formulation of wideband case 90

Equivalent treatment in the frequency domain • Wideband channel = Many narrowband channels H(t) H(f) Noise level f 91

Extensions • • Optimal power allocation Optimal rate allocation Space-time codes Distributed antenna systems • Many, many more! 92

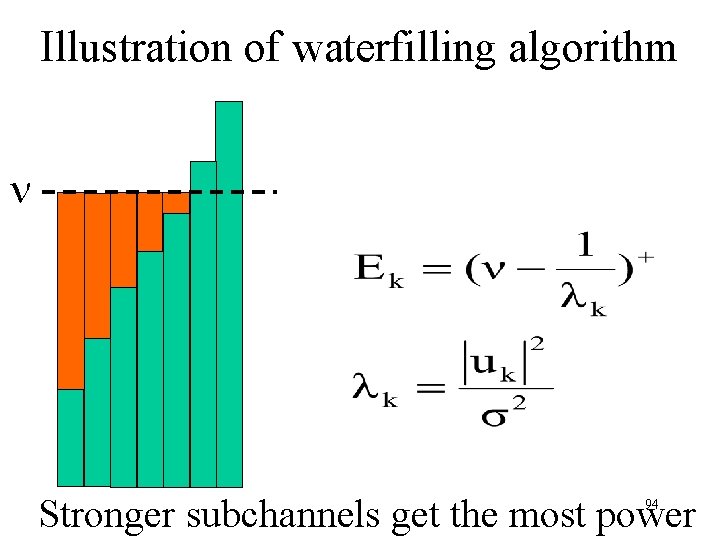
Optimal power allocation • IF the transmitter knows the channel, it can allocate power so as to maximize capacity • Solution: Waterfilling 93

Illustration of waterfilling algorithm Stronger subchannels get the most power 94

• Criterion: Shannon capacity Discussion onmaximization waterfilling (All the SISO discussion on coding, constellation limitations etc is pertinent) • Benefit depends on the channel, available power etc. Correlation, available power Benefit • Limitations: – Waterfilling requires feedback link – FDD/ TDD – Channel state changes 95

Optimal rate allocation • Similar to optimal power allocation • Criterion: throughput (T) maximization • Bk : bits per symbol (depends on constellation size) • Idea: for a given k, find maximum Bk for a target probability of error Pe 96

Discussion on optimal rate allocation • Possible limits on constellation sizes! • Constellation sizes are quantized!!! • The answer is different for different target probabilities of error • Optimal power AND rate allocation schemes possible, but complex 97

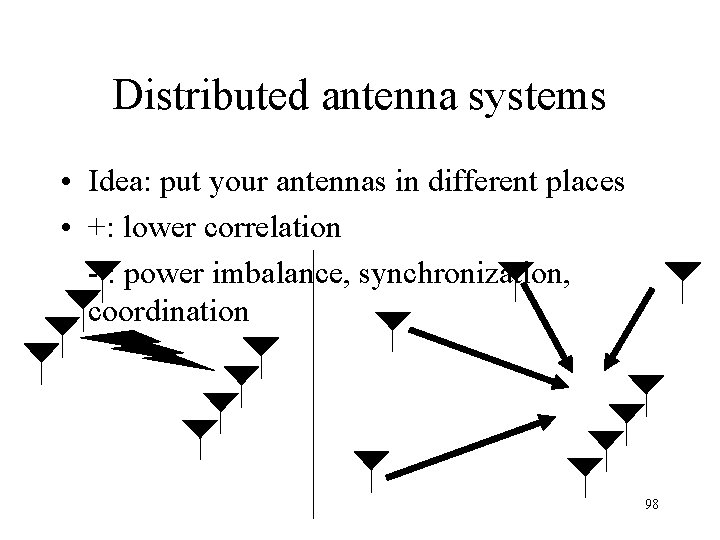
Distributed antenna systems • Idea: put your antennas in different places • +: lower correlation - : power imbalance, synchronization, coordination 98

Practical considerations • • Coding Detection algorithms Channel estimation Interference 99

Detection algorithms • Maximum likelihood linear detector y = H x + n xest = H+y H+ = (HH H)-1 HH : Pseudo inverse of H • Problem: find nearest neighbor among QM points (Q: constellation size, M: number of transmitters) • VERY high complexity!!! 100

Solution: BLAST algorithm • BLAST: Bell Labs l. Ayered Space Time • Idea: NON-LINEAR DETECTOR – Step 1: H+ = (HH H)-1 HH – Step 2: Find the strongest signal (Strongest = the one with the highest post detection SNR) – Step 3: Detect it (Nearest neighbor among Q) – Step 4: Subtract it – Step 5: if not all yet detected, go to step 2 101

Discussion on the BLAST algorithm • It’s a non-linear detector!!! • Two flavors – V-BLAST (easier) – D-BLAST (introduces space-time coding) • Achieves 50 -60% of Shannon capacity • Error propagation possible • Very complicated for wideband case 102

Codingachievable limitations • Capacity = Maximum data rate that can be achieved over the channel with arbitrarily low probability of error • SISO case: – Constellation limitations – Turbo- coding can get you close to Shannon!!! • MIMO case: – Constellation limitations as well – Higher complexity – Space-time codes: very few!!!! 103

Channel estimation • The channel is not perfectly estimated because – it is changing (environment, user movement) – there is noise DURING the estimation • An error in the channel transfer characteristics can hurt you – in the decoding – in the water-filling • Trade-off: Throughput vs. Estimation accuracy • What if interference (as noise) is not white? ? 104

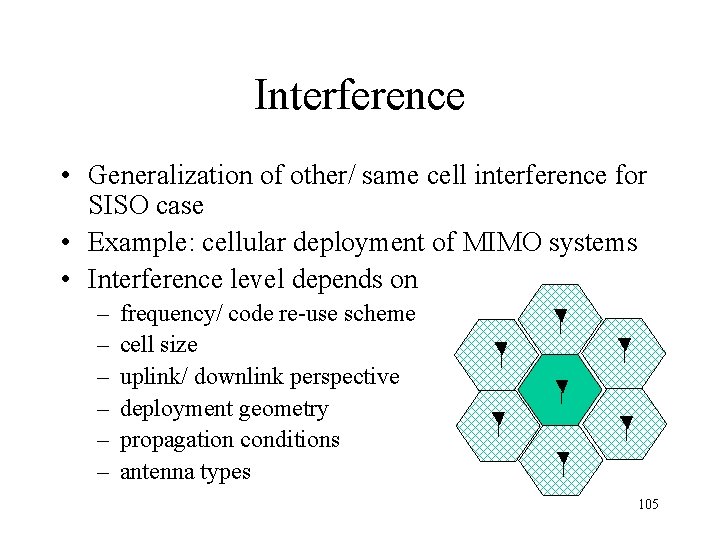
Interference • Generalization of other/ same cell interference for SISO case • Example: cellular deployment of MIMO systems • Interference level depends on – – – frequency/ code re-use scheme cell size uplink/ downlink perspective deployment geometry propagation conditions antenna types 105

Summary and conclusions • MIMO systems are a promising technique for high data rates • Their efficiency depends on the channel between the transmitters and the receivers (power and correlation) • Practical issues need to be resolved • Open research questions need to be answered 106