16 4 Calculations Involving Colligative Properties Chapter 16

16. 4 Calculations Involving > Colligative Properties Chapter 16 Solutions 16. 1 Properties of Solutions 16. 2 Concentrations of Solutions 16. 3 Colligative Properties of Solutions 16. 4 Calculations Involving Colligative Properties 1 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties CHEMISTRY & YOU How hot is a pot of boiling pasta? Recall that dissolved salt elevates the boiling point of water. 2 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Molality and Mole Fraction What are two ways of expressing the ratio of solute to solvent in a solution? 3 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Recall that colligative properties of solutions depend only on the number of solute particles dissolved in a given amount of solvent. 4 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Chemists use two ways to express the ratio of solute particles to solvent particles: in molality and in mole fractions. 5 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Molality (m) is the number of moles of solute dissolved in 1 kilogram (1000 grams) of solvent. 6 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Molality (m) is the number of moles of solute dissolved in 1 kilogram (1000 grams) of solvent. • Molality is also known as molal concentration. 7 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Molality (m) is the number of moles of solute dissolved in 1 kilogram (1000 grams) of solvent. • Molality is also known as molal concentration. moles of solute Molality (m) = kilogram of solvent 8 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Molality is not the same as molarity. • Molality refers to moles of solute per kilogram of solvent rather than moles of solute per liter of solution. 9 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 Using Molality How many grams of potassium iodide must be dissolved in 500. 0 g of water to produce a 0. 060 molal KI solution? 10 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 1 Analyze List the knowns and the unknown. • According to the definition of molality, the final solution must contain 0. 060 mol KI per 1000 g H 2 O. • Use the molality as a conversion factor to convert from mass of the solvent (H 2 O) to moles of the solute (KI). • Then use the molar mass of KI to convert from mol KI to g KI. 11 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 1 Analyze List the knowns and the unknown. The steps are as follows: mass of H 2 O → mol KI → g KI. KNOWNS mass of water = 500. 0 g = 0. 5000 kg solution concentration = 0. 060 m molar mass KI = 166. 0 g/mol UNKNOWN mass of solute = ? g KI 12 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 2 Calculate Solve for the unknown. Identify the conversion factor based on 0. 060 m that allows you to convert from g H 2 O to mol KI. 0. 060 mol KI 1. 000 kg H 2 O 13 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 2 Calculate Solve for the unknown. Identify the conversion factor based on the molar mass of KI that allows you to convert from mol KI to g KI. 166. 0 g KI 1 mol KI 14 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 2 Calculate Solve for the unknown. Multiply the known solvent volume by the conversion factors. To make the 0. 060 -molal KI solution, you would dissolve 5. 0 g of KI in 500. 0 g of water. 0. 060 mol KI 166. 0 g KI 0. 5000 kg H 2 O = 5. 0 g KI 1. 000 kg H 2 O 1 mol KI 15 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 7 3 Evaluate Does the result make sense? • A 1 -molal KI solution is one molar mass of KI (166. 0 g) dissolved in 1000 g of water. • The desired molal concentration (0. 060 m) is about 1/20 of that value, so the mass of KI should be much less than the molar mass. • The answer is correctly expressed to two significant figures. 16 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties The concentration of a solution can also be expressed as a mole fraction. • The mole fraction of a solute in a solution is the ratio of the moles of that solute to the total number of moles of solvent and solute. 17 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties In a solution containing n. A mol of solute A and n. B mol of solvent B, the mole fraction of solute A (XA) and the mole fraction of solvent B (XB) can be expressed as follows: n. A XA = n + n A B 18 n. B XB = n. A + n. B Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Note that mole fraction is a dimensionless quantity. • The sum of the mole fractions of all the components in a solution equals unity, or one. n. A XA = n + n A B 19 n. B XB = n. A + n. B Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Molality and Mole Fraction > Colligative Properties Ethylene glycol (EG) is added to water as antifreeze. • The figure below illustrates how to calculate the mole fractions of the solute and solvent for a solution of EG in water. 20 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 Calculating Mole Fractions Ethylene glycol (EG, or C 2 H 6 O 2) is added to automobile cooling systems to protect against cold weather. What is the mole fraction of each component in a solution containing 1. 25 mol of ethylene glycol and 4. 00 mol of water? 21 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 1 Analyze List the knowns and the unknowns. • The given quantities of solute (EG) and solvent (water) are expressed in moles. • Use the equations for mole fraction of a solute and mole fraction of a solvent to solve this problem. 22 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 1 Analyze List the knowns and the unknowns. KNOWNS moles of ethylene glycol (n. EG) = 1. 25 mol EG moles of water (n. H 2 O) = 4. 00 mol H 2 O UNKNOWNS mole fraction EG (XEG) = ? mole fraction H 2 O (XH 2 O) = ? 23 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 2 Calculate Solve for the unknowns. Write the equation for the mole fraction of ethylene glycol (XEG) in the solution. n. EG XEG = n + n EG H 24 Note that the denominator for each mole fraction is the same: the total number of moles of solvent and solute in the solution. 2 O Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 2 Calculate Solve for the unknowns. Write the equation for the mole fraction of water (XH 2 O) in the solution. Note that the denominator for each mole fraction is the same: the total number of moles of solvent and solute in the solution. n H 2 O X H 2 O = n + n EG H 2 O 25 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 2 Calculate Solve for the unknowns. Substitute the known values into each equation. n. EG XEG = n + n EG H 2 O 1. 25 mol = 1. 25 mol + 4. 00 mol = 0. 238 n H 2 O 4. 00 mol X H 2 O = n + n = 1. 25 mol + 4. 00 mol = 0. 762 EG H 2 O 26 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 8 3 Evaluate Does the result make sense? • The sum of the mole fractions of all the components in the solution equals 1 (XEG + XH 2 O = 1. 000). • Each answer is correctly expressed to three significant figures. 27 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties What is the mole fraction of He in a gaseous solution containing 4. 0 g of He, 6. 5 g of Ar, and 10. 0 g of Ne? A. 0. 60 B. 1. 5 C. 0. 20 D. 0. 11 28 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties What is the mole fraction of He in a gaseous solution containing 4. 0 g of He, 6. 5 g of Ar, and 10. 0 g of Ne? A. 0. 60 B. 1. 5 C. 0. 20 D. 0. 11 29 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Freezing-Point Depression > and Boiling-Point Elevation Colligative Properties Freezing-Point Depression and Boiling-Point Elevation How are freezing-point depression and boiling-point elevation related to molality? 30 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Freezing-Point Depression > and Boiling-Point Elevation Colligative Properties Depressions of freezing points and elevations of boiling points are usually quite small. • To measure colligative properties accurately, you would need a thermometer that can measure temperatures to the nearest 0. 001°C. 31 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Freezing-Point Depression > and Boiling-Point Elevation Colligative Properties Depressions of freezing points and elevations of boiling points are usually quite small. • Another way to determine the magnitudes of colligative properties is by calculating them. • You can do this if you know the molality of the solution and some reference data about the solvent. 32 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Freezing-Point Depression > and Boiling-Point Elevation Colligative Properties The magnitudes of the freezing-point depression (ΔTf) and the boiling-point elevation (ΔTb) of a solution are directly proportional to the molal concentration (m), assuming the solute is molecular, not ionic. 33 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Freezing-Point Depression > and Boiling-Point Elevation Colligative Properties The magnitudes of the freezing-point depression (ΔTf) and the boiling-point elevation (ΔTb) of a solution are directly proportional to the molal concentration (m), assuming the solute is molecular, not ionic. 34 ΔTf m ΔTb m Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

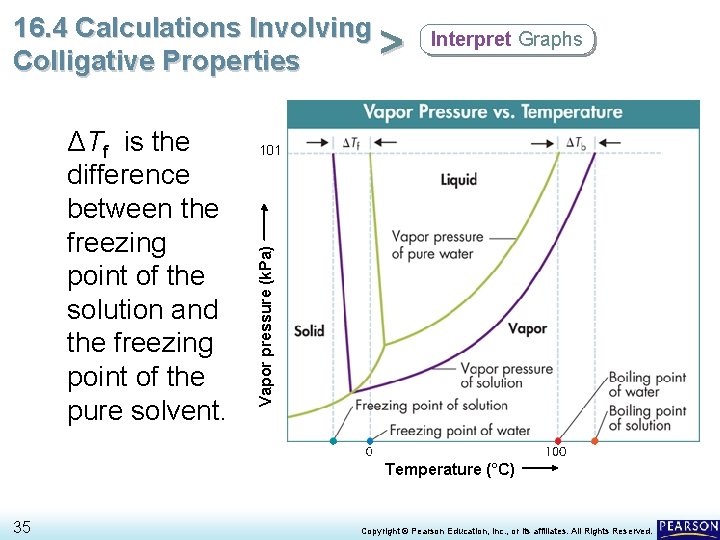
16. 4 Calculations Involving > Colligative Properties 101 Vapor pressure (k. Pa) ΔTf is the difference between the freezing point of the solution and the freezing point of the pure solvent. Interpret Graphs Temperature (°C) 35 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

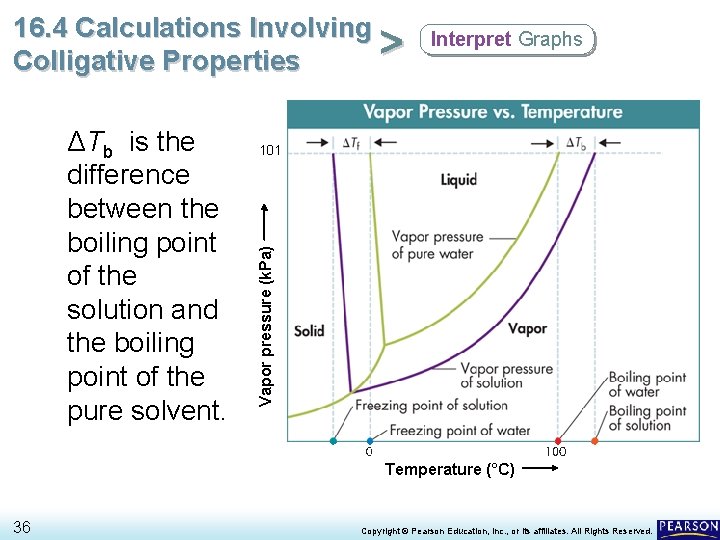
16. 4 Calculations Involving > Colligative Properties 101 Vapor pressure (k. Pa) ΔTb is the difference between the boiling point of the solution and the boiling point of the pure solvent. Interpret Graphs Temperature (°C) 36 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

Freezing-Point Depression 16. 4 Calculations Involving > and Boiling-Point Elevation Colligative Properties With the addition of a constant, the proportionality between the freezing-point depression and the molality m can be expressed as an equation. ΔTf = Kf m 37 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

Freezing-Point Depression 16. 4 Calculations Involving > and Boiling-Point Elevation Colligative Properties With the addition of a constant, the proportionality between the freezing-point depression and the molality m can be expressed as an equation. ΔTf = Kf m • The constant, Kf, is the molal freezing-point depression constant, which is equal to the change in freezing point for a 1 -molal solution of a nonvolatile molecular solute. 38 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

Freezing-Point Depression 16. 4 Calculations Involving > and Boiling-Point Elevation Colligative Properties The boiling-point elevation of a solution can also be expressed as an equation. ΔTb = Kb m 39 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

Freezing-Point Depression 16. 4 Calculations Involving > and Boiling-Point Elevation Colligative Properties The boiling-point elevation of a solution can also be expressed as an equation. • The proportionality constant is Kb, the molal boiling-point depression constant, which is equal to the change in boiling point for a 1 -molal solution of a nonvolatile molecular solute. ΔTb = Kb m 40 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

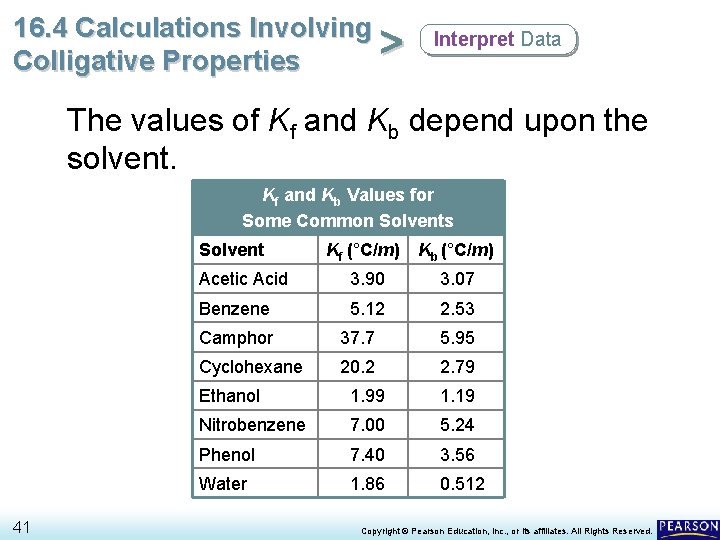
16. 4 Calculations Involving > Colligative Properties Interpret Data The values of Kf and Kb depend upon the solvent. Kf and Kb Values for Some Common Solvents Solvent 41 Kf (°C/m) Kb (°C/m) Acetic Acid 3. 90 3. 07 Benzene 5. 12 2. 53 Camphor 37. 7 5. 95 Cyclohexane 20. 2 2. 79 Ethanol 1. 99 1. 19 Nitrobenzene 7. 00 5. 24 Phenol 7. 40 3. 56 Water 1. 86 0. 512 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 9 Calculating the Freezing-Point Depression of a Solution Antifreeze protects a car from freezing. It also protects it from overheating. Calculate the freezing-point depression of a solution containing exactly 100 g of ethylene glycol (C 2 H 6 O 2) antifreeze in 0. 500 kg of water. 42 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 9 1 Analyze List the knowns and the unknown. • Calculate the number of moles of C 2 H 6 O 2 and the molality of the solution. • Then calculate the freezing-point depression using ΔTf = Kf m. UNKNOWNS mass of C 2 H 6 O 2 = 100 g ΔTf = ? °C mass of water = 0. 500 kg Kf for H 2 O = 1. 86°C/m 43 molar mass C 2 H 6 O 2 = 62. 0 g/mol Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 9 2 Calculate Solve for the unknown. • Use the molar mass of C 2 H 6 O 2 to convert the mass of solute to moles. 100 g C 2 H 6 O 2 1 mol C 2 H 6 O 2 62. 0 g C 2 H 6 O 2 = 1. 61 mol C 2 H 6 O 2 • Calculate the molality of the solution. mol solute 1. 61 mol m = kg solvent = 0. 500 kg 44 = 3. 22 m Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 9 2 Calculate Solve for the unknown. Calculate the freezing-point depression. ΔTf = Kf m = 1. 86°C/m 3. 22 m = 5. 99°C The freezing point of the solution is 0. 00 o. C – 5. 99°C = – 5. 99°C. 45 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 9 3 Evaluate Does the result make sense? • A 1 -molal solution reduces the freezing temperature by 1. 86°C. • So, a decrease of 5. 99°C for an approximately 3 -molal solution is reasonable. 46 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 10 Calculating the Boiling Point of a Solution What is the boiling point of a 1. 50 m Na. Cl solution? 47 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 10 1 Analyze List the knowns and the unknown. • Each formula unit of Na. Cl dissociates into two particles, according to the equation Na. Cl(s) → Na+(aq) + Cl–(aq). • Based on the total number of dissociated particles, the effective molality is 2 1. 50 m = 3. 00 m. • Calculate the boiling-point elevation (using the equation ΔTb = Kb m) and then add it to 100°C. KNOWNS UNKNOWN Solution concentration = 1. 50 m Na. Cl boiling point = ? °C Kb for H 2 O = 0. 512°C/m 48 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 10 2 Calculate Solve for the unknown. • Calculate the boiling-point elevation, making sure to use the molality of total dissociated particles in solution. ΔTb = Kb m = 0. 512°C/m 3. 00 m = 1. 54°C • Calculate the boiling point of the solution. Tb = 100°C + 1. 54°C = 101. 54°C 49 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties Sample Problem 16. 10 3 Evaluate Does the result make sense? • The boiling point increases about 0. 5°C for each mole of solute particles. • The total change is reasonable. • Because the boiling point of water is defined as exactly 100°C, this value does not limit the number of significant figures in the solution of the problem. 50 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties CHEMISTRY & YOU Does pasta cook at 100°C? After you read Sample Problem 16. 10, calculate the boiling-point elevation for 2 L of water containing a teaspoon of salt (about 20 g). 51 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties CHEMISTRY & YOU Does pasta cook at 100°C? After you read Sample Problem 16. 10, calculate the boiling-point elevation for 2 L of water containing a teaspoon of salt (about 20 g). 1 mol Na. Cl 2 mol solute 20 g Na. Cl 58. 5 g Na. Cl 1 mol Na. Cl = 0. 7 mol solute 0. 7 mol m = kg solvent = 2 kg = 0. 4 m ΔTb = Kb m = 0. 512°C/m 0. 4 m = 0. 2°C 52 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties How does the freezing-point depression by Ca. Cl 2 for a given solvent compare to the freezing-point depression caused by the same molal concentration of ethylene glycol (C 2 H 6 O 2, )? A. It is exactly the same. B. It is twice as large. C. It is three times as large. D. It is four times as large. 53 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties How does the freezing-point depression by Ca. Cl 2 for a given solvent compare to the freezing-point depression caused by the same molal concentration of ethylene glycol (C 2 H 6 O 2, )? A. It is exactly the same. B. It is twice as large. C. It is three times as large. D. It is four times as large. 54 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Key Concepts > Colligative Properties Chemists use two ways to express the ratio of solute to solvent: in molality and in mole fractions. The magnitudes of freezing-point depression and boiling-point elevation are proportional to molality. 55 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Key Equations > Colligative Properties moles of solute Molality (m) = kilograms of solvent n. A Mole fractions: XA = n. A + n. B XB = n. A + n. B ΔTf = Kf m ΔTb = Kb m 56 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving Glossary Terms > Colligative Properties • molality (m): the concentration of solute in a solution expressed as the number of moles of solute dissolved in 1 kilogram (1000 g) of solvent • mole fraction: the ratio of the moles of solute in solution to the total number of moles of both solvent and solute • molal freezing-point depression constant (Kf): the change in freezing point for a 1 -molal solution of a nonvolatile molecular solute • molal boiling-point elevation constant (Kb): the change in boiling point for a 1 -molal solution of a nonvolatile molecular solute 57 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties BIG IDEA The Mole and Quantifying Matter Solution concentration can be quantified in terms of molarity (moles of solute per liter of solution), molality (moles of solute per kilogram of solvent), percent by volume, and percent by mass. 58 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.

16. 4 Calculations Involving > Colligative Properties END OF 16. 4 59 Copyright © Pearson Education, Inc. , or its affiliates. All Rights Reserved.