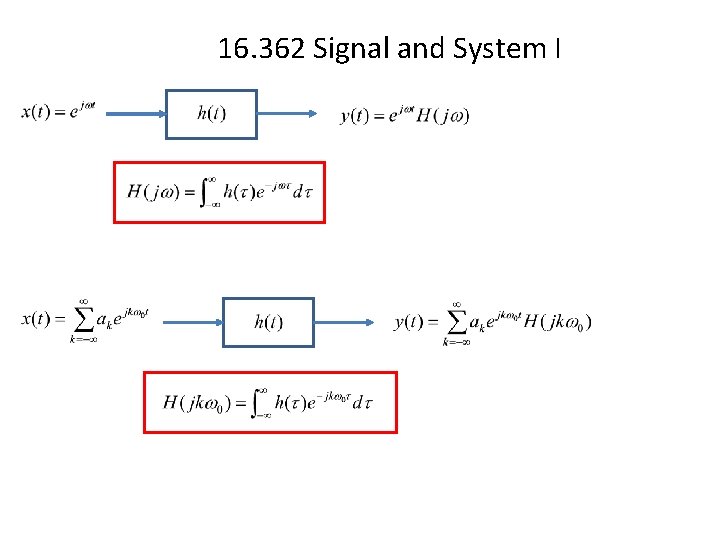
16 362 Signal and System I The unit
![16. 362 Signal and System I Example N=4 [1, 2, 2, 1] [1, 1,](https://slidetodoc.com/presentation_image_h/783141b734dc66bc3f122bf9af1e93f7/image-21.jpg "16. 362 Signal and System I Example N=4 [1, 2, 2, 1] [1, 1,")
- Slides: 55
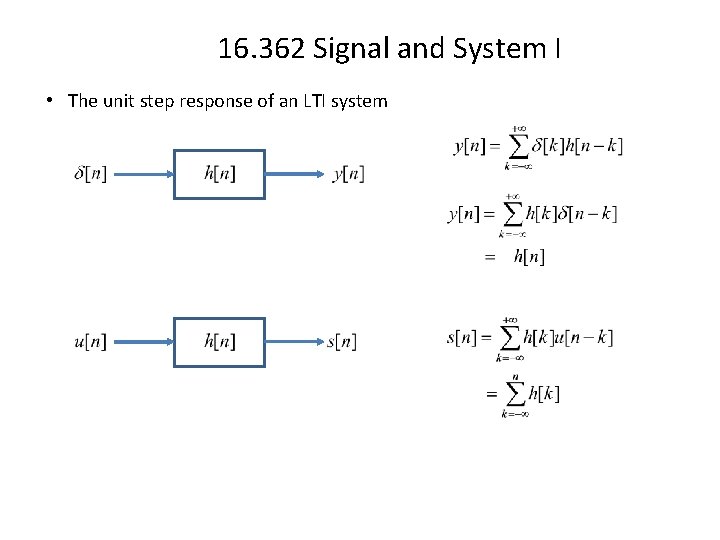
16. 362 Signal and System I • The unit step response of an LTI system
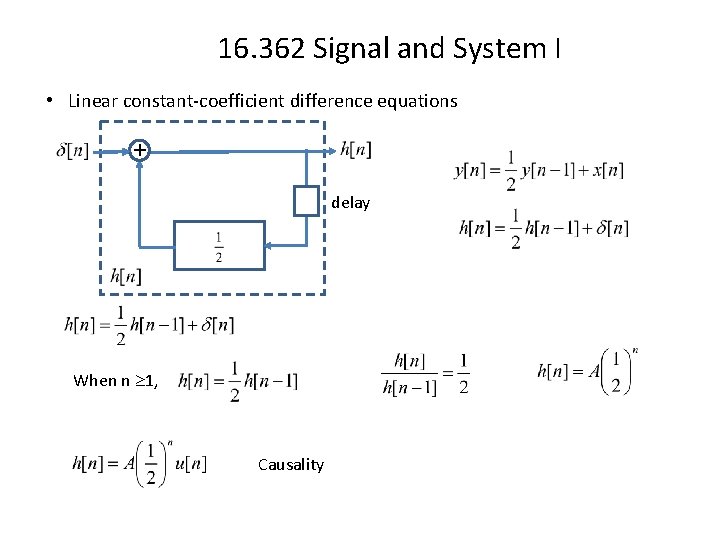
16. 362 Signal and System I • Linear constant-coefficient difference equations + delay When n 1, Causality
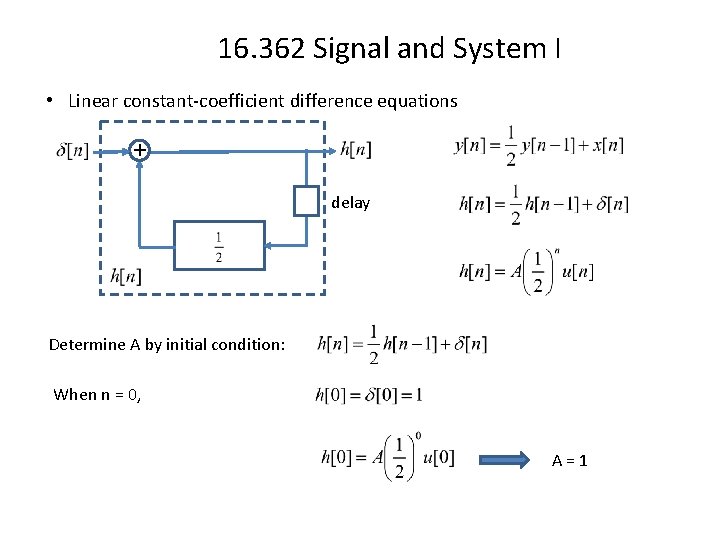
16. 362 Signal and System I • Linear constant-coefficient difference equations + delay Determine A by initial condition: When n = 0, A=1
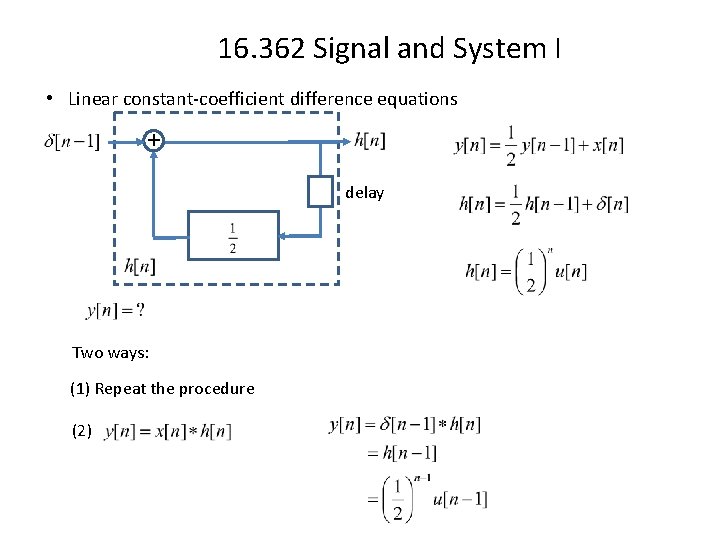
16. 362 Signal and System I • Linear constant-coefficient difference equations + delay Two ways: (1) Repeat the procedure (2)
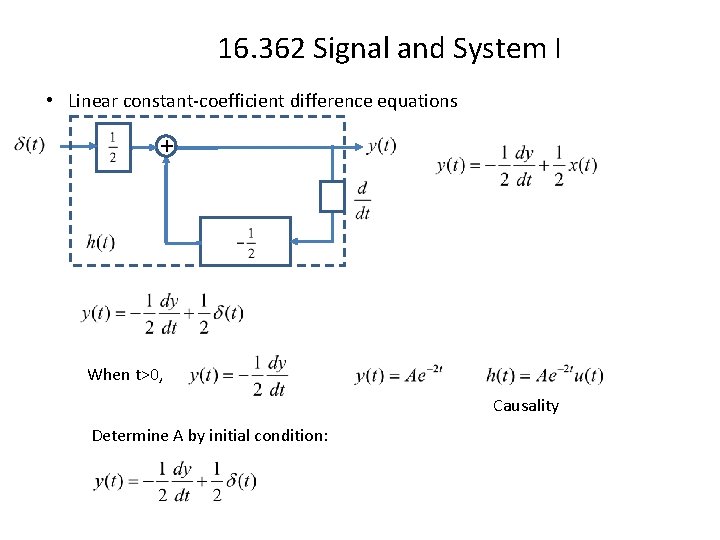
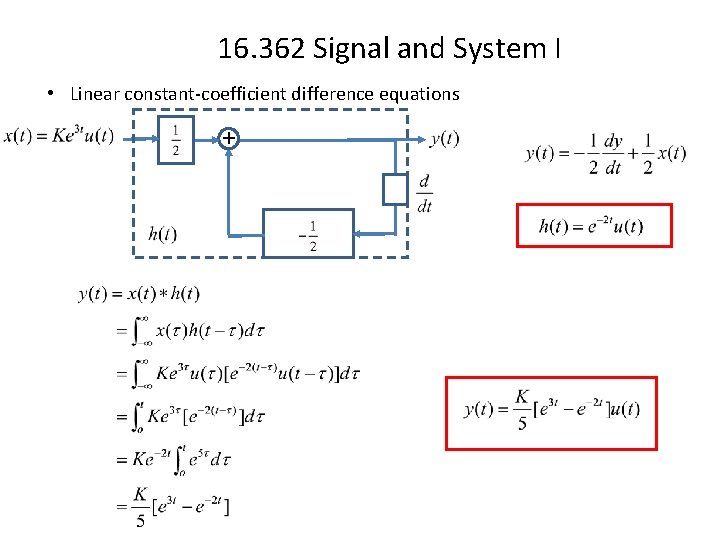
16. 362 Signal and System I • Linear constant-coefficient difference equations + When t>0, Causality Determine A by initial condition:
16. 362 Signal and System I • Linear constant-coefficient difference equations + Determine A by initial condition: A=1
16. 362 Signal and System I • Linear constant-coefficient difference equations +
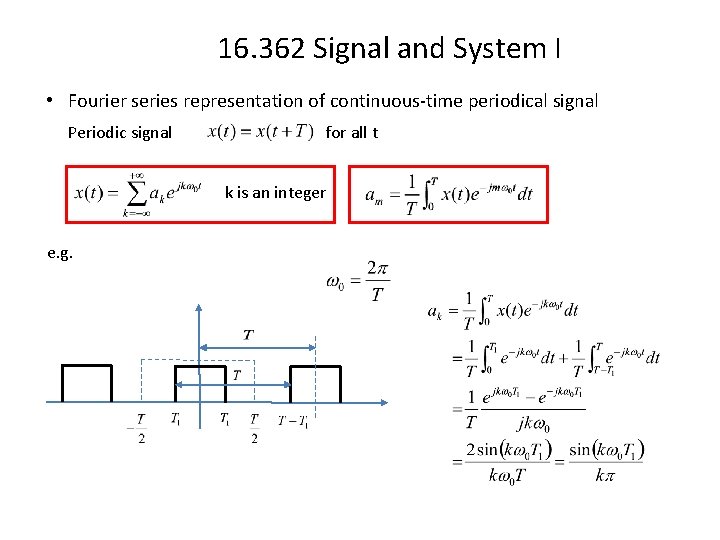
16. 362 Signal and System I • Fourier series representation of continuous-time periodical signal Periodic signal for all t k is an integer Fourier series form a complete and orthogonal bases Complete: no other basis is needed. Orthogonal: Kronecker Delta Orthogonal:
16. 362 Signal and System I • Fourier series representation of continuous-time periodical signal Periodic signal for all t k is an integer
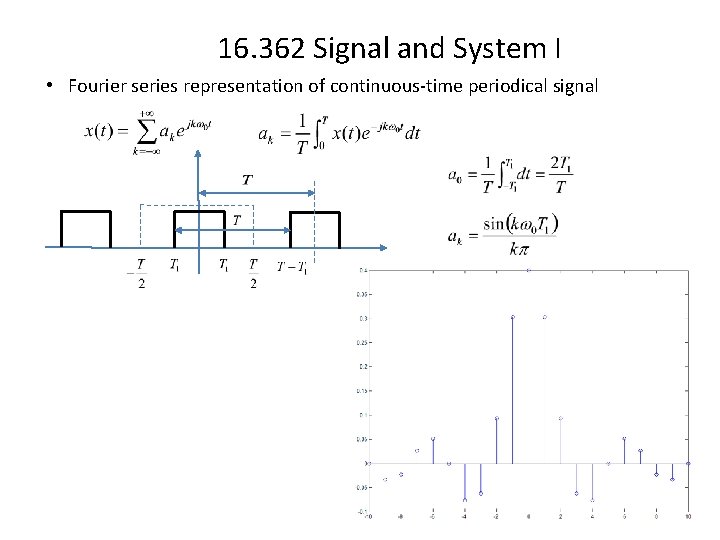
16. 362 Signal and System I • Fourier series representation of continuous-time periodical signal Periodic signal for all t k is an integer e. g.
16. 362 Signal and System I • Fourier series representation of continuous-time periodical signal 0
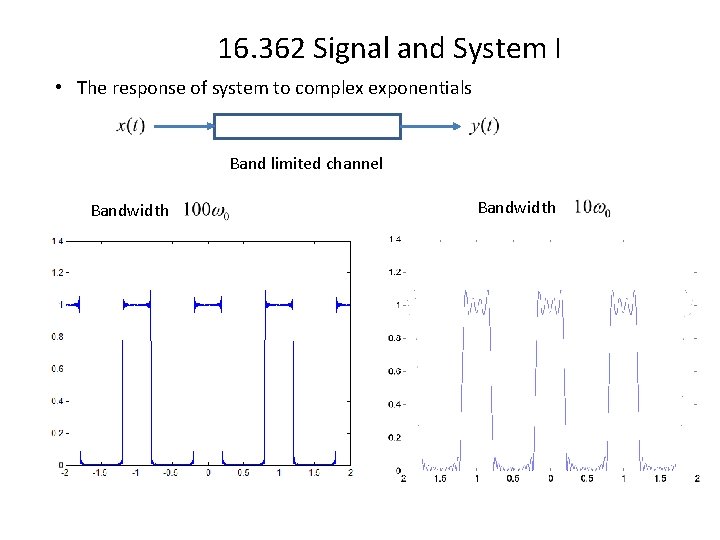
16. 362 Signal and System I • The response of system to complex exponentials Band limited channel Bandwidth
16. 362 Signal and System I • Fourier series representation of discrete-time periodical signal Periodic signal for all t
16. 362 Signal and System I • Example #1
16. 362 Signal and System I • Properties of discrete-time Fourier series (1) Linearity
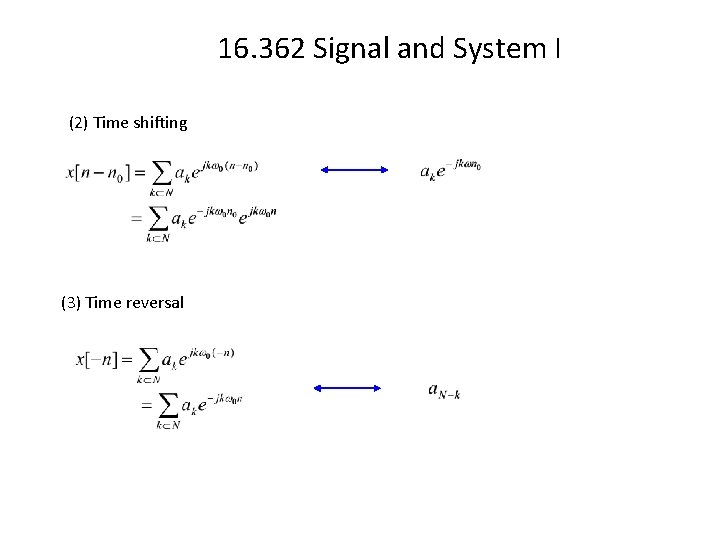
16. 362 Signal and System I (2) Time shifting (3) Time reversal
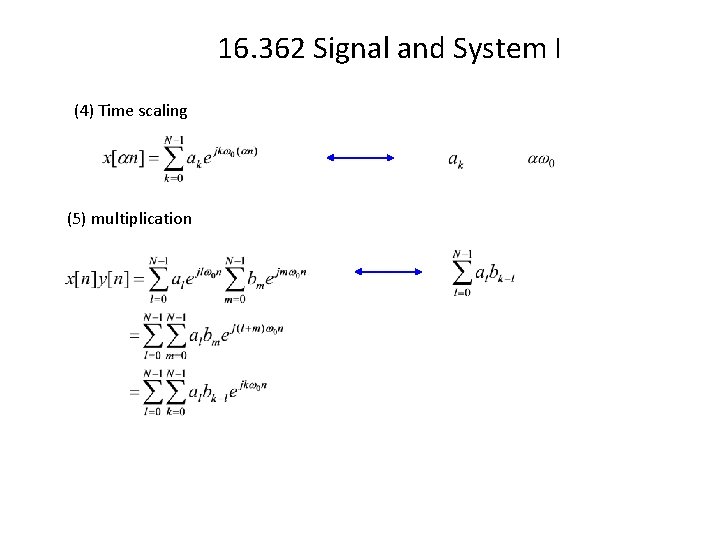
16. 362 Signal and System I (4) Time scaling (5) multiplication
16. 362 Signal and System I (6) Conjugation and conjugate symmetry Real signal Even Real & Even
16. 362 Signal and System I (7) Parseval’s relation
16. 362 Signal and System I (8) Time difference (9) Running sum
16. 362 Signal and System I Example N=4 [1, 2, 2, 1] [1, 1, 1, 1]
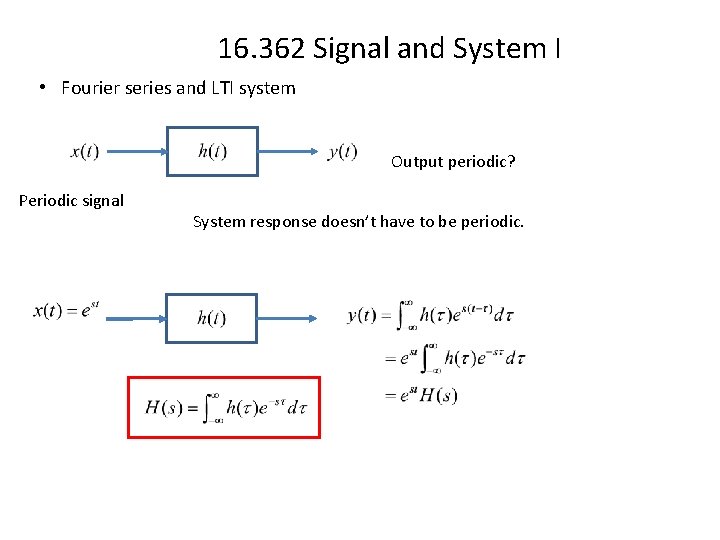
16. 362 Signal and System I • Fourier series and LTI system Output periodic? Periodic signal System response doesn’t have to be periodic.
16. 362 Signal and System I
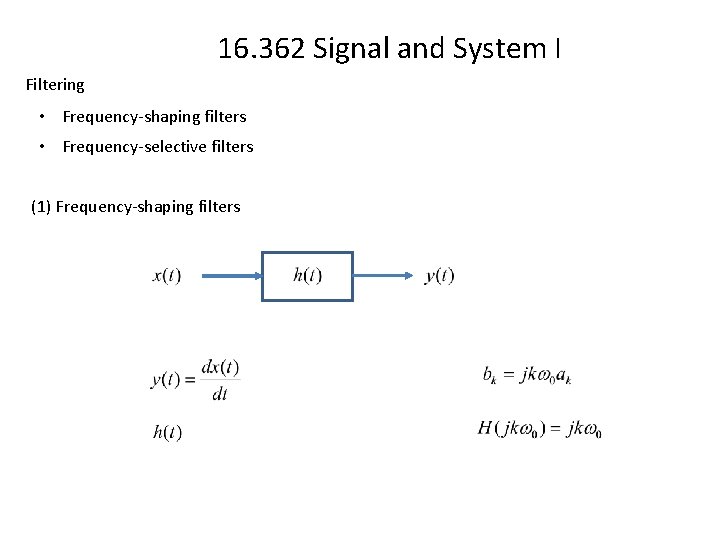
16. 362 Signal and System I Filtering • Frequency-shaping filters • Frequency-selective filters (1) Frequency-shaping filters
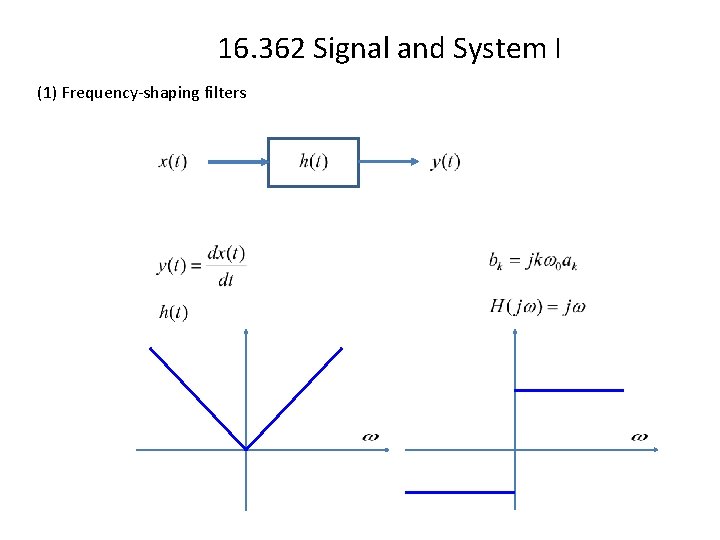
16. 362 Signal and System I (1) Frequency-shaping filters
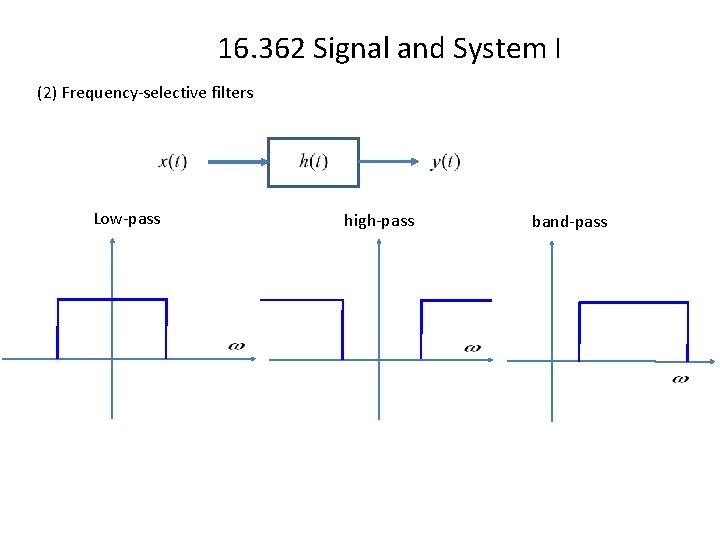
16. 362 Signal and System I (2) Frequency-selective filters Low-pass high-pass band-pass
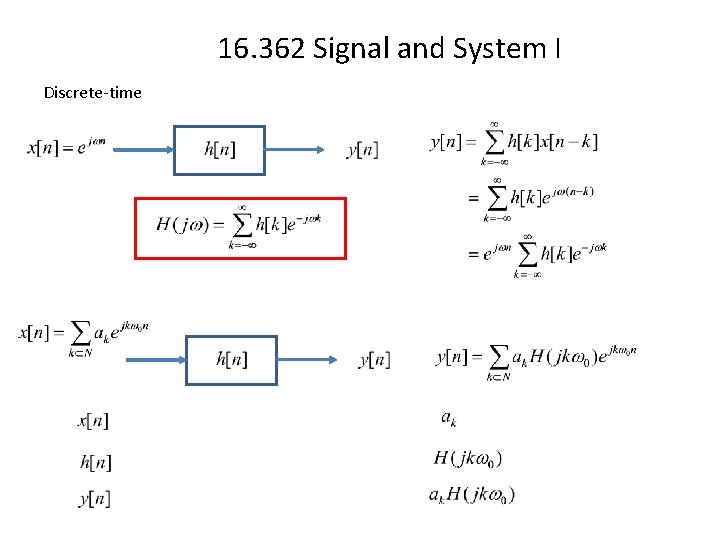
16. 362 Signal and System I Discrete-time
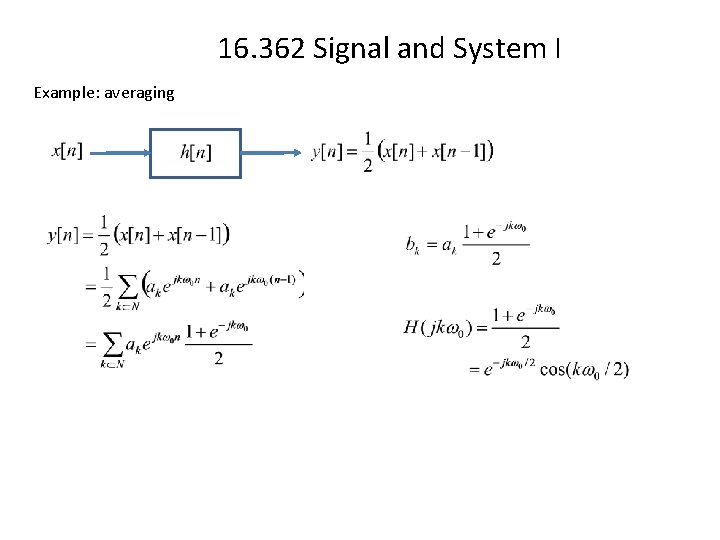
16. 362 Signal and System I Example: averaging
16. 362 Signal and System I • Continuous-time Fourier transform Aperiodic signal Periodic signal k is an integer
16. 362 Signal and System I • Continuous-time Fourier transform Aperiodic signal Periodic signal k is an integer
16. 362 Signal and System I • Examples
16. 362 Signal and System I • Properties of continuous-time Fourier transform (1) Linearity
16. 362 Signal and System I • Properties of continuous-time Fourier transform (2) Time shifting (3) Time reversal
16. 362 Signal and System I • Properties of continuous-time Fourier transform (4) Time scaling
16. 362 Signal and System I • Properties of continuous-time Fourier transform (5) Conjugation and conjugate summary Real
16. 362 Signal and System I Example even Even and real
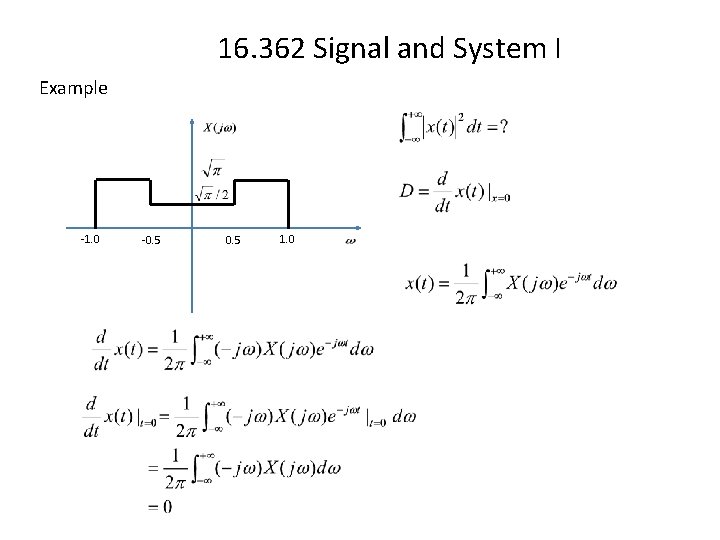
16. 362 Signal and System I Differential
Integral 16. 362 Signal and System I
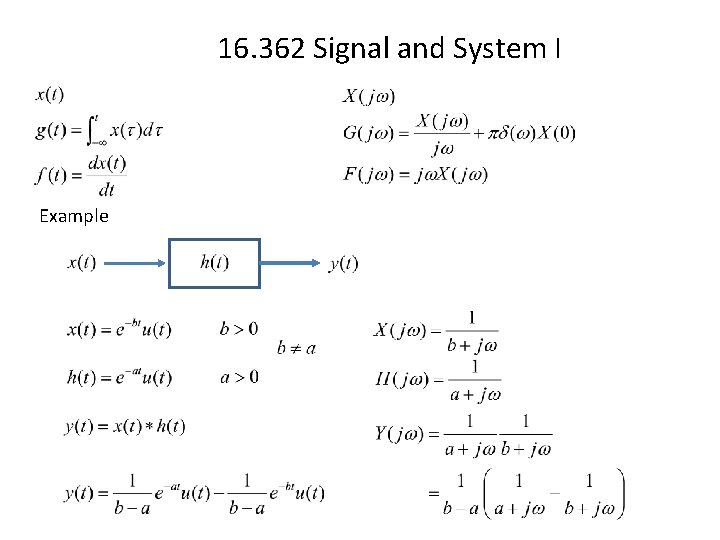
16. 362 Signal and System I Example
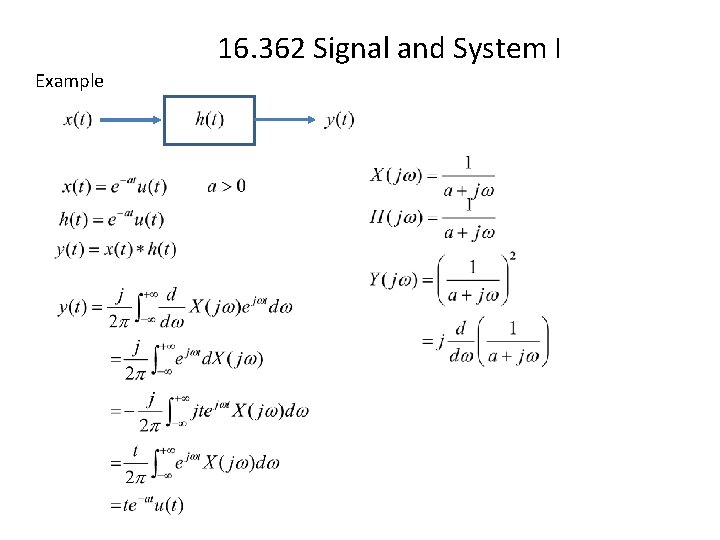
16. 362 Signal and System I Example
16. 362 Signal and System I Example
16. 362 Signal and System I Example
16. 362 Signal and System I Parseval’s relation
16. 362 Signal and System I Parseval’s relation for continuous-time Fourier series Parseval’s relation for continuous-time Fourier transfer
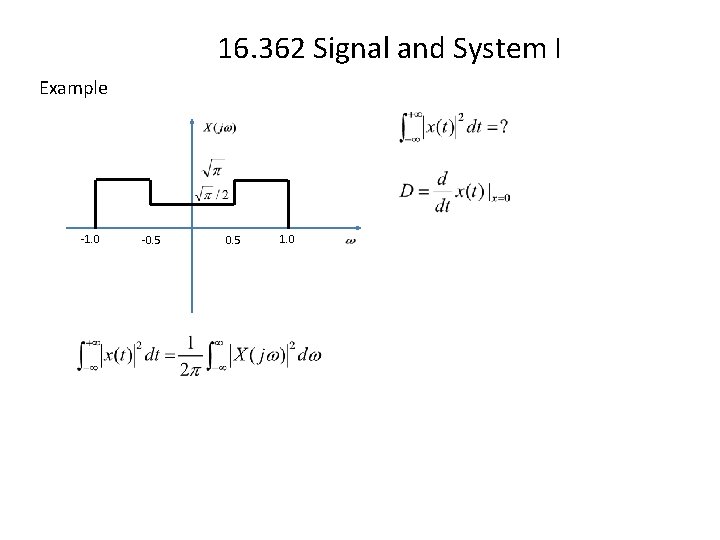
16. 362 Signal and System I Example -1. 0 -0. 5 1. 0
16. 362 Signal and System I Example -1. 0 -0. 5 1. 0
Example, P. 4. 14 (1) real (2) (3) Solution: 16. 362 Signal and System I
Example, P. 4. 14 (1) real (2) (3) Solution: 16. 362 Signal and System I
Example, P. 4. 14 Solution: 16. 362 Signal and System I
Example, P. 4. 14 (3) Solution: 16. 362 Signal and System I
Example, P. 4. 14 (3) Solution: (1) real 16. 362 Signal and System I
16. 362 Signal and System I • Multiplication
16. 362 Signal and System I Example #1
16. 362 Signal and System I Example #2
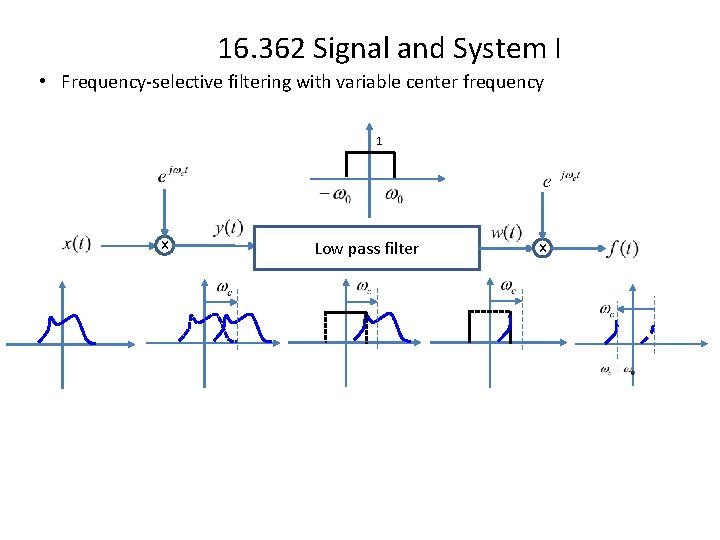
16. 362 Signal and System I • Frequency-selective filtering with variable center frequency 1 x Low pass filter x