16 1 Solubility Equilibria Ksp Chapter 15 AcidBase

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Solubility Equilibria • Ionic compounds reach an equilibrium when they dissolve. A(s) C+(aq) + D-(aq) Dissolution Precipitation • Dissociation equation: An equation that describes how an ionic substance dissolves. • Solubility Equilibria – The point at which dissolution and precipitation are occurring at the same rate. This represents the saturation point of the solute.

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria The Solubility Product, Ksp • Solubility equilibria are calculated just like reaction equilibria. • For the dissociation equation: a. A(s) ⇄ b. B(aq) + c. C(aq) the equilibrium expression can be expressed as [B]b[C]c Keq = [A]a Remember that pure solids and liquids are NOT included in the Keq. so, for a solution the equilibrium constant or “solubility product”, is Ksp = [B]b[C]c Ksp, like all Keq values, is temperature dependent.

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Solubility v. Solubility-Product Constant Solubility = amount of a solute that will dissolve in a stated quantity of solvent to produce a saturated solution. • units are typically: ◊ grams/liter of solvent (g/L) ◊ moles/liter of solvent (mol/L) • when calculating solubility, you can use the mole ratio of the dissociation equation Mg. Cl 2(s) ⇄ Mg 2+(aq) + 2 Cl−(aq) ◊ the solubility of Mg. Cl 2 is equal to the amount of Mg 2+ at equilibrium (1: 1 ratio) ◊ the solubility of Mg. Cl 2 is equal to ½ the amount of Cl− at equilibrium (1: 2 ratio)

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Solubility v. Solubility-Product Constant = equilibrium constant between ionic solid and ion concentrations at saturation • no units for Ksp values ◊ Small Ksp = substance not very soluble (little product) ◊ Large Ksp = substance very soluble (lot of product) • relative Ksp’s can be used to compare solubilities of salts with similar ion ratios Formula Ksp Ag. I(s) 1. 5 x 10− 16 Cu. I(s) 5. 0 x 10− 12 Ca. SO 4(s) 6. 1 x 10− 5 smallest Ksp least soluble largest Ksp most soluble • this does not hold if comparing salts with different ion ratios ◊ for example: Cu. S(s) & Ag 2 S(s)

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Calc # 1: Calculating Ksp from Solubility A sample of Mg. F 2(s) is added to pure water and allowed to come to equilibrium at 25 o. C. The concentration of Mg 2+ is 1. 17 x 10 -3 M at equilibrium. What is the value of Ksp for Mg. F 2? 1. Write the equilibrium equation for the salt. Mg. F 2(s) ⇌ Mg 2+(aq) + 2 F–(aq) 2. Write the solubility-product expression. Ksp = [Mg 2+][F–]2 3. Substitute the concentrations & solve. The concentration of F- will be 2 x the concentration of Mg 2+ because the mole ratio of F– to Mg 2+ is 2: 1 Ksp = [1. 17 x 10 -3][ 2. 34 x 10 -3]2 = 6. 41 x 10 -9

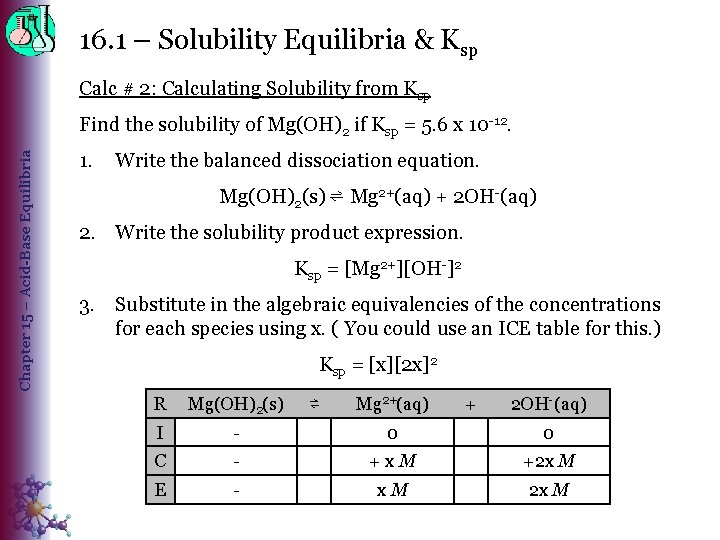
16. 1 – Solubility Equilibria & Ksp Calc # 2: Calculating Solubility from Ksp Chapter 15 – Acid-Base Equilibria Find the solubility of Mg(OH)2 if Ksp = 5. 6 x 10 -12. 1. Write the balanced dissociation equation. Mg(OH)2(s) ⇌ Mg 2+(aq) + 2 OH-(aq) 2. Write the solubility product expression. Ksp = [Mg 2+][OH-]2 3. Substitute in the algebraic equivalencies of the concentrations for each species using x. ( You could use an ICE table for this. ) Ksp = [x][2 x]2 R Mg(OH)2(s) I - 0 0 C - +x. M +2 x M E - x. M 2 x M ⇌ Mg 2+(aq) + 2 OH-(aq)

16. 1 – Solubility Equilibria & Ksp Calc # 2: Calculating Solubility from Ksp Chapter 15 – Acid-Base Equilibria Find the solubility of Mg(OH)2 if Ksp = 5. 6 x 10 -12. 4. Solve for x. Ksp = 5. 6 x 10 -12= 4 x 3 x = 1. 1 x 10 -4 x = [Mg 2+] = 1. 1 x 10 -4 ; [OH-] = 2 x = 2. 2 x 10 -4 Mg(OH)2(s) ⇌ Mg 2+(aq) + 2 OH-(aq) Because 1 mol of Mg 2+ is produced for each 1 mol of Mg(OH)2 dissolved, the solubility of Mg(OH)2 is 1. 1 x 10 -4 mol/liter. This could be converted into grams/liter if requested. 1. 1 x 10 -4 mol Mg(OH)2 58. 319 g Mg(OH)2 liter 1 mol Mg(OH)2 = 0. 0064 g/L

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Common- Ion Effect Generally, the solubility of a slightly soluble salt is decreased by the presence of a second solute that contains an ion in common with the slightly soluble salt. Ca. F 2(s) ⇌ Ca 2+(aq) + 2 F–(aq) For Example: Ca. F 2(s) ⇌ Ca 2+(aq) + 2 F–(aq) + Ca(NO 3)2(s) ⇌ Ca 2+(aq) + 2 NO 3–(aq)

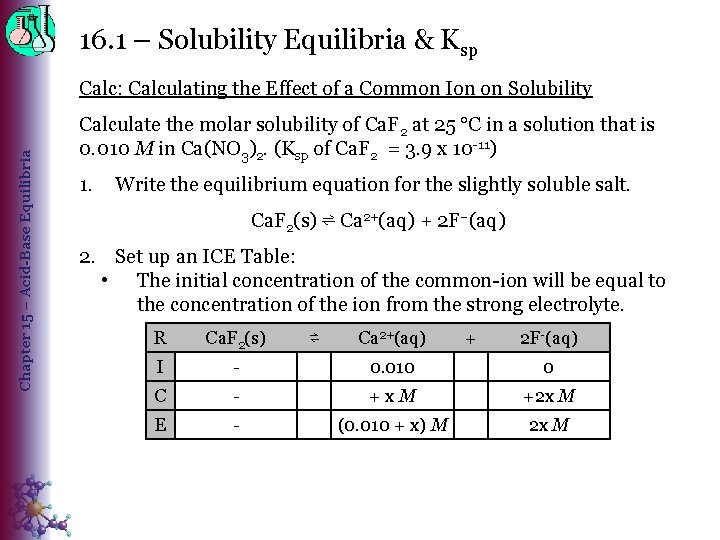
16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Calc: Calculating the Effect of a Common Ion on Solubility Calculate the molar solubility of Ca. F 2 at 25 C in a solution that is 0. 010 M in Ca(NO 3)2. (Ksp of Ca. F 2 = 3. 9 x 10 -11) 1. Write the equilibrium equation for the slightly soluble salt. Ca. F 2(s) ⇌ Ca 2+(aq) + 2 F–(aq) 2. Set up an ICE Table: • The initial concentration of the common-ion will be equal to the concentration of the ion from the strong electrolyte. R Ca. F 2(s) I - 0. 010 0 C - +x. M +2 x M E - (0. 010 + x) M 2 x M ⇌ Ca 2+(aq) + 2 F-(aq)

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Calc: Calculating the Effect of a Common Ion on Solubility Calculate the molar solubility of Ca. F 2 at 25 C in a solution that is 0. 010 M in Ca(NO 3)2. (Ksp of Ca. F 2 = 3. 9 x 10 -11) 3. Write the equilibrium equation for the slightly soluble salt. Ksp = [Ca 2+][F–]2 Consider the normal solubility of Ca. F 2 3. 9 x 10 -11 = x(2 x)2 ; x = 2. 1 x 10 -4 (not very soluble) 4. Disregarding the small contribution of Ca 2+ from the dissolution of Ca. F 2 and substituting: 3. 9 x 10 -11 = [0. 010][2 x]2 x = 3. 1 x 10 -5 M Note: The solubility of Ca. F 2 (2. 1 x 10 -4) is reduced by the presence of the common ion Ca 2+ as expected.

16. 1 – Solubility Equilibria & Ksp Chapter 15 – Acid-Base Equilibria Solubility and p. H If the anion of the solute is basic, the solubility of the salt will increase as p. H is lowered. • Basic anions: carbonate, phosphate, cyanide, sulfide, fluoride, hydroxide ◊ These are anions (conjugate bases) of weak acids. • Salts whose anions are the anions of strong acids are unaffected by p. H. ◊ Cl–, Br–, I–, NO 3–, Cl. O 4–, Cl. O 3–, HSO 4– Na. F(s) ⇌ Na+(aq) + F–(aq) + H 2 O(s) ⇌ H+(aq) + OH–(aq) H+(aq) + F–(aq) ⇌ HF(aq) Na. F(s) ⇌ Na+(aq) + F–(aq)

16. 2 – Precipitation & Qualitative Analysis Chapter 15 – Acid-Base Equilibria The Ion Product (Qsp) The ion product for a solution is its reaction quotient. • Q may be calculated to determine the saturation condition of the solution at a given moment in time. ◊ If Qsp > Ksp : too much solute Ø solution is supersaturated, precipitation will occur ◊ If Qsp < Ksp : too little solute Ø solution is unsaturated, dissolution may continue ◊ If Qsp = Ksp : solution is at equilibrium (saturated)

16. 2 – Precipitation & Qualitative Analysis Chapter 15 – Acid-Base Equilibria Predicting Precipitation To determine if a precipitate will form, the concentrations of ions from combined solutions may be substituted into the Ksp expression. Example: A solution is prepared using 750. 0 m. L of 4. 00× 10– 3 M Ce(NO 3)3 and 300. 0 m. L of 2. 00× 10– 2 M KIO 3. Will Ce(IO 3)3 (Ksp = 1. 9× 10– 10) precipitate from this solution? Ce(NO 3)3 ⇌ Ce 3+(aq) + 3 NO 3–(aq) • The concentration of Ce 3+(aq) = the diluted concentration of Ce(NO 3)3. M 1 V 1 = M 2 V 2 4. 00× 10– 3 M • 750. 0 m. L = M 2 • 1050. 0 m. L M(Ce 3+) = 2. 86× 10– 3 M

16. 2 – Precipitation & Qualitative Analysis Chapter 15 – Acid-Base Equilibria Predicting Precipitation Example: A solution is prepared using 750. 0 m. L of 4. 00× 10– 3 M Ce(NO 3)3 and 300. 0 m. L of 2. 00× 10– 2 M KIO 3. Will Ce(IO 3)3 (Ksp = 1. 9× 10– 10) precipitate from this solution? KIO 3 ⇌ K+(aq) + IO 3–(aq) • The concentration of IO 3−(aq) = the diluted concentration of KIO 3. M 1 V 1 = M 2 V 2 2. 00× 10– 2 M • 300. 0 m. L = M 2 • 1050. 0 m. L M(IO 3−) = 5. 71× 10– 3 M Ce(IO 3)3 (s) ⇄ Ce 3+(aq) + 3 IO 3−(aq) Qsp = [Ce 3+][IO 3−]3 = [2. 86× 10– 3][5. 71× 10– 3]3 = 5. 32× 10– 10 since Qsp > Ksp, precipitate forms.

16. 2 – Precipitation & Qualitative Analysis Chapter 15 – Acid-Base Equilibria Selective Precipitation of Ions Using differences in solubility with a common added ion to initiate precipitation and separate ions. • Ksp values and Ksp expressions determine the concentration of the common ion needed to precipitate each salt. Example: To separate Ag+(aq) and Pb 2+(aq) from solution, Cl–(aq) may be added to initiate precipitation. Ag. Cl(s) ⇌ Ag+(aq) + Cl–(aq) ; Ksp = 1. 8 x 10 -10 Pb. Cl 2(s) ⇌ Pb 2+(aq) + 2 Cl–(aq) ; Ksp = 1. 7 x 10 -5 • The salt with the lowest Ksp (Ag. Cl) is the least soluble and would precipitate first. ◊ When evaluating Ksp to determine the species that will precipitate first, watch out for species higher in stoichiometric proportions – you may have to complete calculations to determine the first PPT.

16. 2 – Precipitation & Qualitative Analysis Chapter 15 – Acid-Base Equilibria Qualitative Analysis = testing for presence/absence of ions 1. Ions thought to be present are grouped based on solubility 2. Ions are selectively precipitated using different solutions 3. Ions are separated by using specific tests. Grouping Ions • Group 1: (Add HCl) ◊ Insoluble chlorides: Ag+, Hg 22+, Pb 2+ • Group 2: (Add H 2 S & HCl) ◊ Acid-insoluble sulfides: Cu 2+, Bi 3+, Cd 2+, Pb 2+, Hg 2+, As 3+, Sb 3+, Sn 4+ • Group 3: Add (NH 4)2 S at p. H 8 ◊ Base-insoluble sulfides & hydroxides: Al 3+, Cr 3+, Fe 3+, Zn 2+, Ni 2+, Co 2+, Mn 2+ • Group 4: Add (NH 4)2 HPO 4 and NH 3 ◊ Insoluble phosphates: Mg 2+, Ca 2+, Sr 2+, Ba 2+ • Group 5: Remaining ions will be alkali metal ions or NH 4+ ◊ Flame tests may be used to determine identities

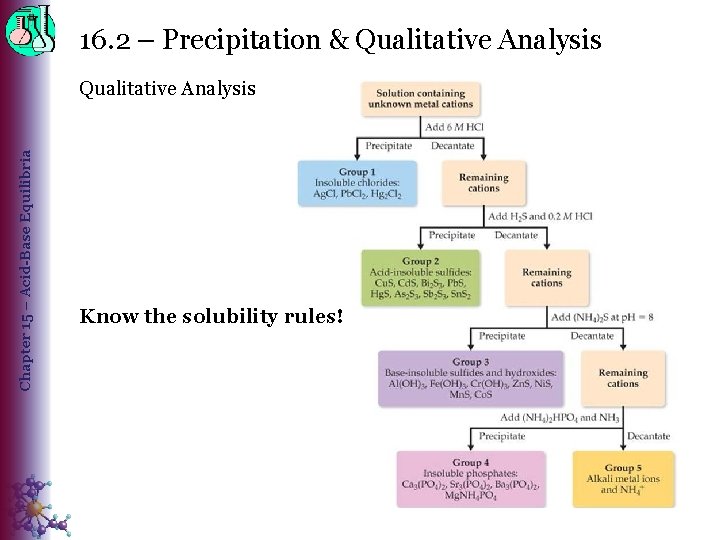
16. 2 – Precipitation & Qualitative Analysis Chapter 15 – Acid-Base Equilibria Qualitative Analysis Know the solubility rules!

16. 3 – Equilibria Involving Complex Ions Chapter 15 – Acid-Base Equilibria Formation of Complex Ions* Transition metal ions can act as Lewis acids • Water molecules and other Lewis bases can react with metal ions to form “metal complexes” ◊ Common complex metals: Al 3+, Ag+, Cu 2+, Zn 2+, Ni 2+, Co 2+ ◊ Lewis bases (aka ligands) often found in complex ions: NH 3, H 2 O, CN–, OH– especially if “concentrated” or “in excess” Ø Rule of thumb: when in doubt, number of ligands = 2 x the charge of the metal cation ◊ Complex ion = an assembly of a metal ion and Lewis bases with a net charge ◊

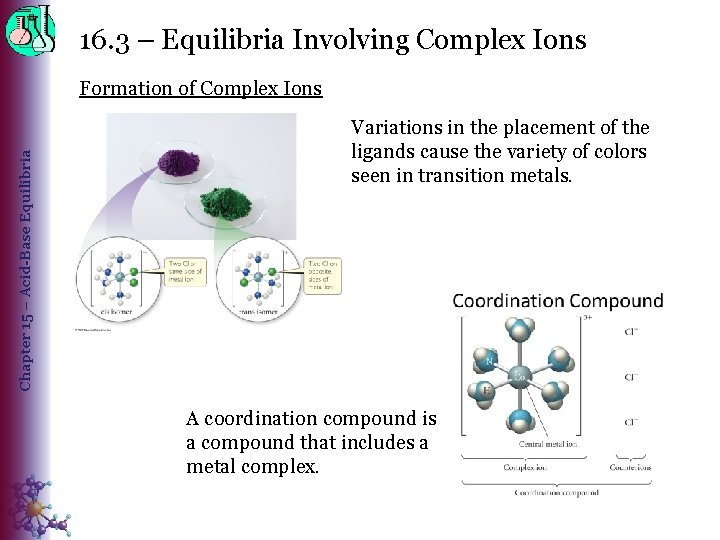
16. 3 – Equilibria Involving Complex Ions Chapter 15 – Acid-Base Equilibria Formation of Complex Ions Variations in the placement of the ligands cause the variety of colors seen in transition metals. A coordination compound is a compound that includes a metal complex.

16. 3 – Equilibria Involving Complex Ions Chapter 15 – Acid-Base Equilibria Formation of Complex Ions Lewis acid-base reactions that result in complex ions can dramatically increase the solubility of a slightly soluble salt. The removal of the cation from solution, as it forms the complex, stresses the equilibrium system and allows more of the compound to dissolve.

16. 3 – Equilibria Involving Complex Ions Chapter 15 – Acid-Base Equilibria Amphoterism Metal oxides (MO) and hydroxides (MOH) that are only slightly soluble dissolve in strongly acidic or basic solutions • Oxides and hydroxides of Al 3+, Zn 2+, Cr 3+, Sn 2+ ◊ dissolve in acidic solutions because they have basic anions ◊ dissolve in strongly basic solutions because they form complex ions involving hydroxides