15 Legendre Functions 1 Legendre Polynomials 2 Orthogonality

15. Legendre Functions 1. Legendre Polynomials 2. Orthogonality 3. Physical Interpretation of Generating Function 4. Associated Legendre Equation 5. Spherical Harmonics 6. Legendre Functions of the Second Kind

Schrodinger eq. for a central potential Associated Legendre eq. with

1. Legendre Polynomials Legendre eq. x = 1 & x = are regular singular points.

Frobenius Series See § 8. 3 & Mathematica Indicial eq. Set a 1 = 0 s = 0 even order : s = 1 odd order : a 2 j + 1 = 0 series diverges for x 2 1 unless terminated

Generating Function

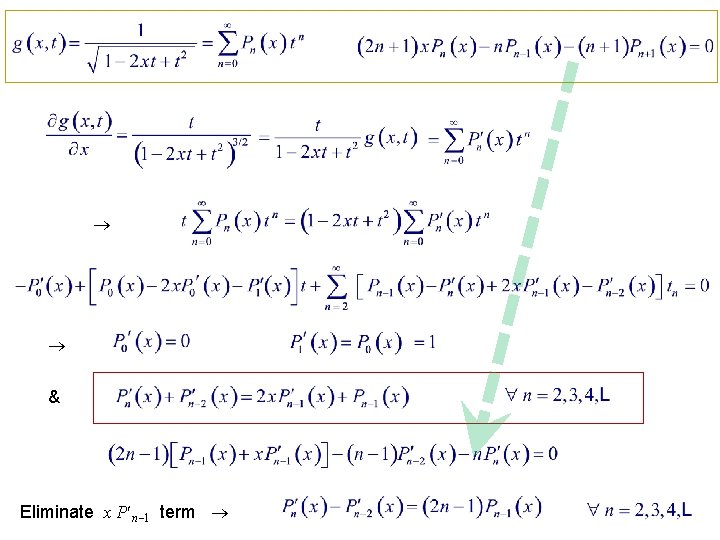
& highest power of x in coeff. of tn is n. Coeff. of xn in Pn(x) = Coeff. of xn tn Coeff. of highest power of x in Pn(x)

Summary Power Expansion : Ex. 15. 1. 2

Recurrence Relations

Table 15. 1. Legendre Polynomials Mathematica

& Eliminate x P n 1 term

More Recurrence Relations Any set of functions satisfying these recurrence relations also satisfy the Legendre ODE. Ex. 15. 1. 1

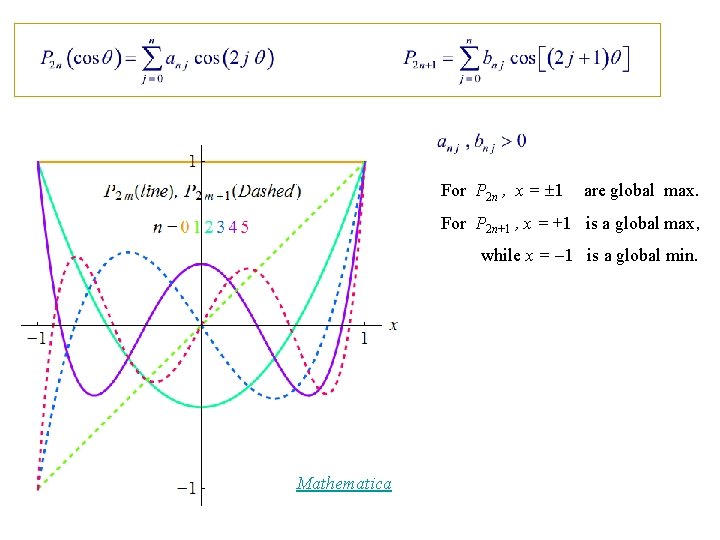
Upper & Lower Bounds for Pn (cos )

Coeff. invariant under j j Coeff. invariant under j ( j+1)

For P 2 n , x = 1 are global max. For P 2 n+1 , x = +1 is a global max, while x = 1 is a global min. Mathematica

Rodrigues Formula From § 12. 1 : If has self-adjoint form then Rodrigues Formula Legendre eq. : Self-adjoint form :

Coefficient of xn in Pn(x) Coefficient of xn is :

2. Orthogonality is self-adjoint [ w(x) = 1 ] Pn(x) are orthogonal polynomials in [ 1, 1 ].

Normalization Let via Rodrigues formula : Ex. 15. 2. 1

Legendre Series Eigenfunctions of an ODE are complete { Pn (x) } is completeness over [ 1, 1]. For any function f (x) in [ 1, 1] : unique

Solutions to Laplace Eq. in Spherical Coordinates General solution : finite l = 0, 1, 2, … Solution with no azimuthal dependence ( m = 0 ) : Solution that is finite inside & outside a boundary sphere :

Example 15. 2. 1 Earth’s Gravitational Field Gravitational potential U in mass-free region : Neglect azimuthal dependence : Earth’s radius at equator g includes rotational effect Note: Let Earth is a sphere al dimensionless

Slightly distorted Earth with axial symmetry : CM located at origin See Mathematica for proof. Experimental data : pear shape Data including longitudinal dependence is described by a Laplace series (§ 15. 5).

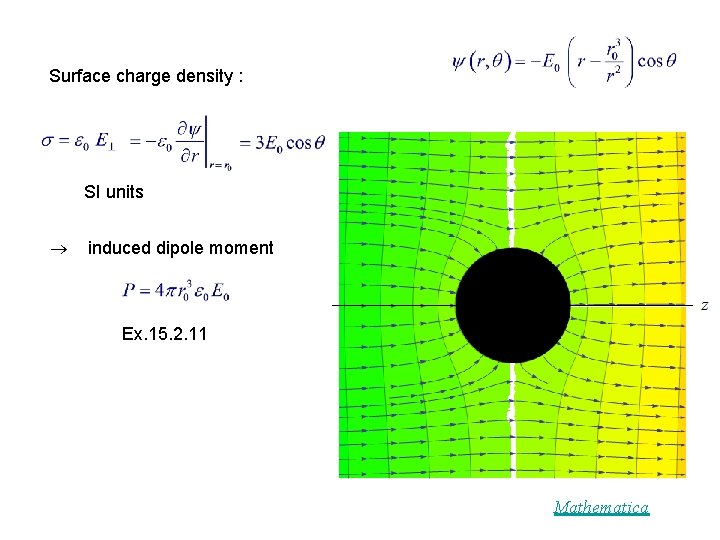
Example 15. 2. 2 Sphere in a Uniform Field Grounded conducting sphere (radius r 0 ) in uniform applied electric field everywhere For :

Surface charge density : SI units induced dipole moment Ex. 15. 2. 11 Mathematica

Example 15. 2. 3 Electrostatic Potential for a Ring of Charge Thin, conducting ring of radius a, centered at origin & lying in x-y plane, has total charge q. Outside the ring, Axial symmetry no dependence For r > a : On z-axis, Coulomb’s law gives : Mathematica

See Eg. 15. 4. 2 for magnetic analog.