15 December 2021 Position vectors LO Identify position

15 December 2021 Position vectors LO: Identify position vectors. www. mathssupport. org
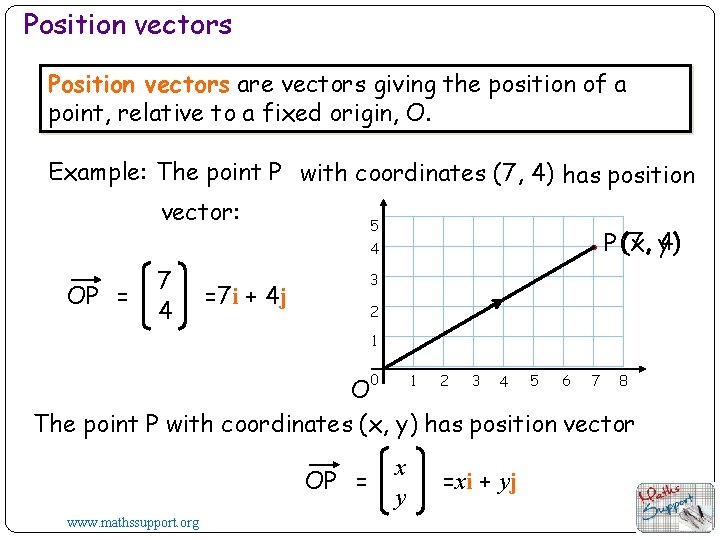
Position vectors are vectors giving the position of a point, relative to a fixed origin, O. Example: The point P with coordinates (7, 4) has position vector: 5 (x, 4) y) P (7, 4 OP = 7 4 3 =7 i + 4 j 2 1 0 6 7 8 5 1 2 3 4 O The point P with coordinates (x, y) has position vector OP = www. mathssupport. org x y =xi + yj
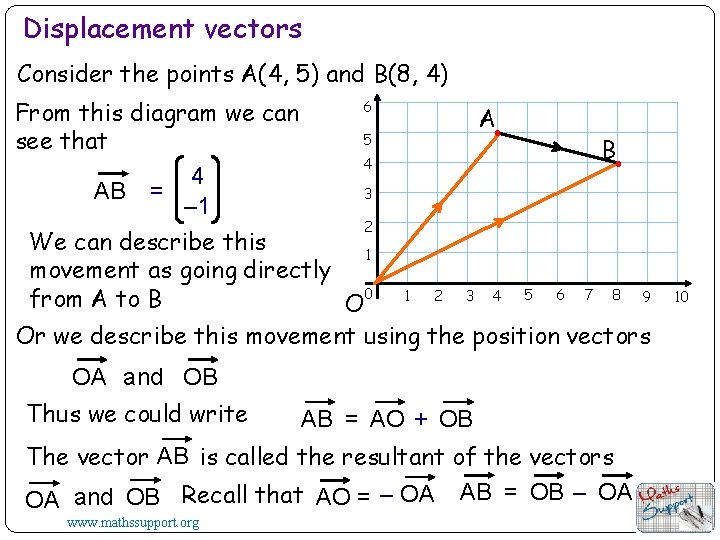
Displacement vectors Consider the points A(4, 5) and B(8, 4) 6 From this diagram we can A 5 see that B 4 4 AB = 3 – 1 2 We can describe this 1 movement as going directly 0 6 7 8 5 1 2 3 4 9 from A to B O Or we describe this movement using the position vectors OA and OB Thus we could write AB = AO + OB The vector AB is called the resultant of the vectors OA and OB Recall that AO = – OA AB = OB – OA www. mathssupport. org 10

Example 1 Points A and B have coordinates (-4, 3, 0) and (-3, 6, 4) respectively. Find the vector AB First we write the position vector OA and OB OA = -4 3 0 OB = -3 AB = OB - OA = 6 4 www. mathssupport. org – -3 6 4 -4 3 0 = 1 3 4

Resultant vectors Similarly if we know a vector PQ and a vector PR then each of the points Q and R are given relative to point P. P R Q We can write: QR = QP + PR = PR – PQ www. mathssupport. org

Example 2 Given that XY = 2 1 -3 Find the vector XZ = YZ YZ = XZ - XY www. mathssupport. org 0 -8 -2 0 = -8 -2 – 2 1 -3 = -2 -9 1

Example 3 Show that the points A, B and C with position vectors i – 2 j + 3 k, – 2 i + 3 j – k and 4 i – 7 j + 7 k respectively are collinear -2 1 4 3 OA = -2 OB = OC = -7 -1 7 3 Find the vector AB -2 AB = OB- OA = 3 – -1 Find the vector AC 4 AC = OC- OA = -7 7 www. mathssupport. org – 1 -2 3 = = -3 5 -4 3 -5 4 AB = – AC
- Slides: 7