15 251 Great Theoretical Ideas in Computer Science





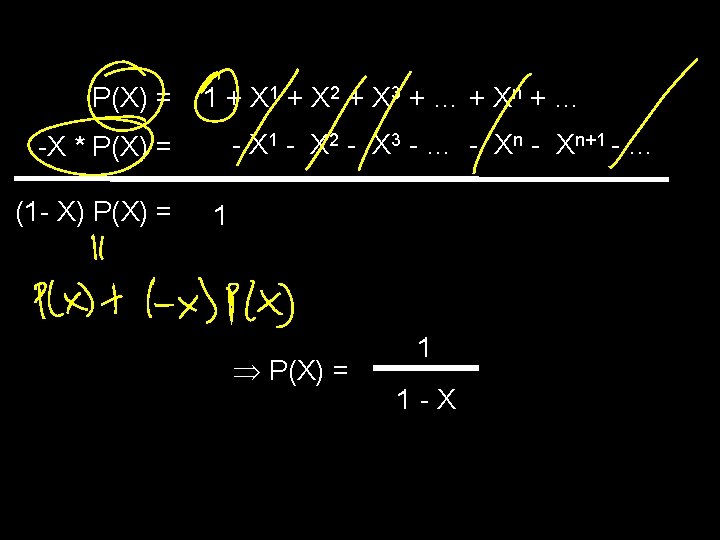









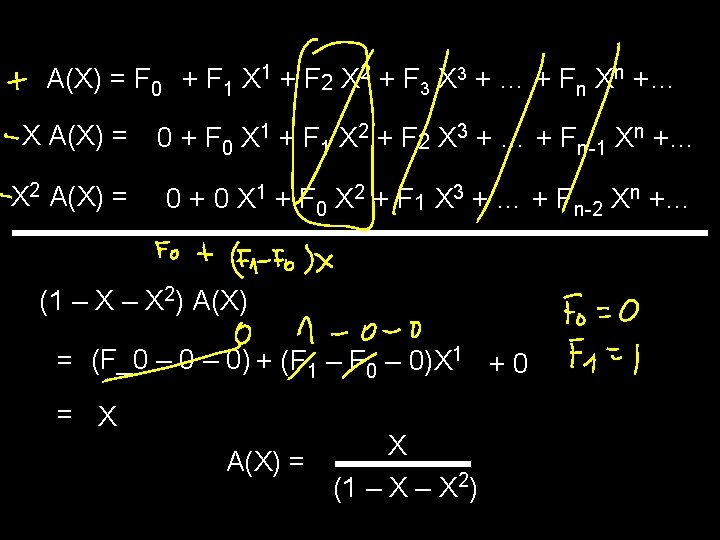









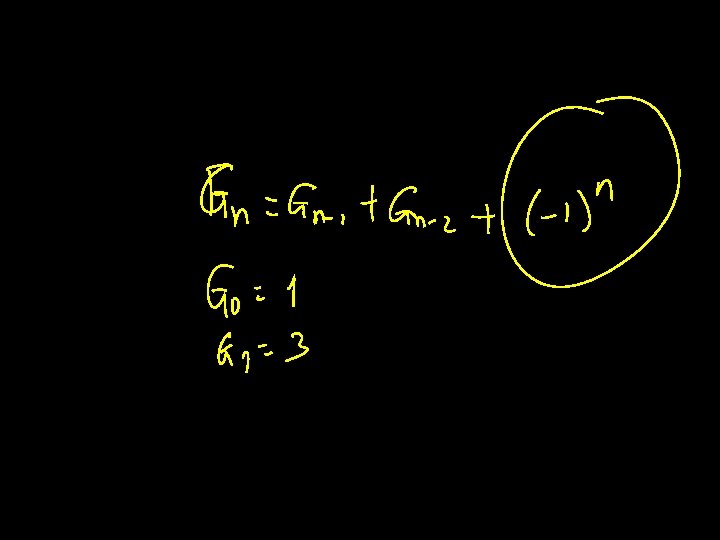









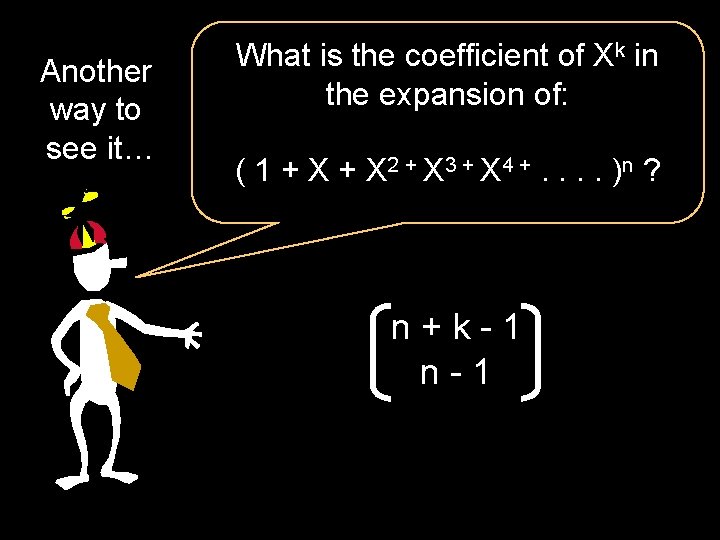



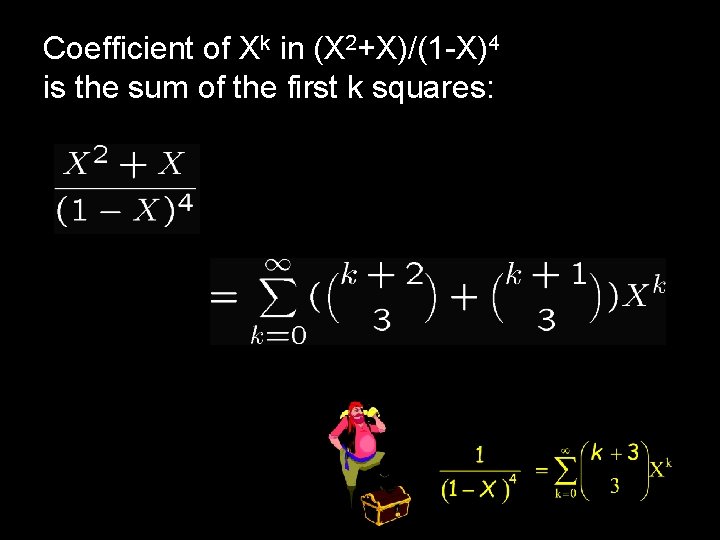
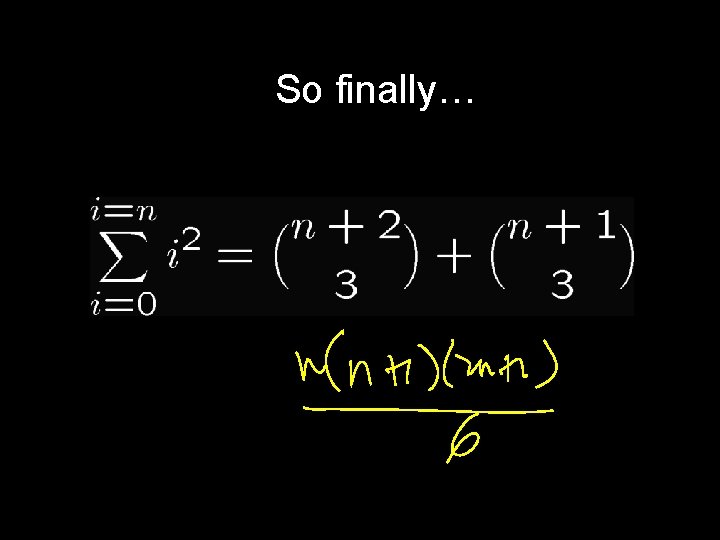











- Slides: 59

15 -251 Great Theoretical Ideas in Computer Science

Counting III: Generating Functions Lecture 8 (February 5, 2009) 1 X+ 2 X+ 3 X

1 + X 2 + X 3 + … + Xn-2 + Xn-1 = = Xn – 1 X-1 1 - Xn 1 -X Recall the Geometric Series

1 + X 2 + X 3 + … + X n + … = 1 1 -X the Infinite Geometric Series Holds when |X| < 1 Also makes sense if we view the infinite sum on the left as a formal power series

Formal Power Series P(X) = i=0 a i. X i
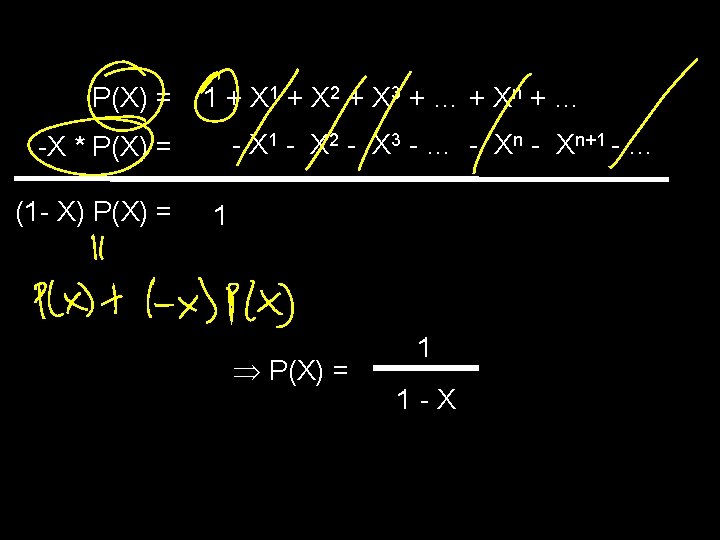

Formal Power Series P(X) = a i. X i i=0 There are no worries about convergence issues. This is a purely syntactic object.

Formal Power Series P(X) = a i. X i i=0 If you want, think of as the infinite vector V = < a 0, a 1, a 2, . . . , an, … > But, as you will see, thinking of as a “polynomial” is very natural.

Operations A(X) = a 0 + a 1 X + a 2 X 2 + … B(X) = b 0 + b 1 X + b 2 X 2 + … adding them together (A+B)(X) = (a 0+b 0) + (a 1+b 1) X + (a 2+b 2) X 2 + … like adding the vectors position-wise <4, 2, 3, …> + <5, 1, 1, …. > = <9, 3, 4, …>

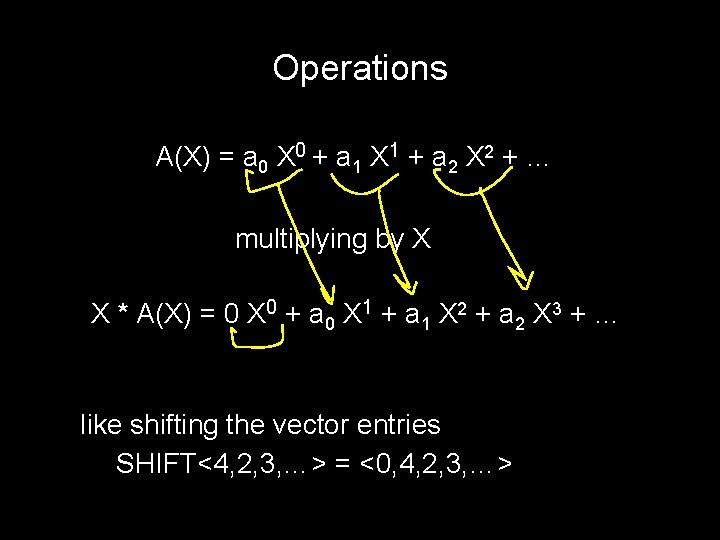
Operations A(X) = a 0 X 0 + a 1 X 1 + a 2 X 2 + … multiplying by X X * A(X) = 0 X 0 + a 0 X 1 + a 1 X 2 + a 2 X 3 + … like shifting the vector entries SHIFT<4, 2, 3, …> = <0, 4, 2, 3, …>

Example: Store: V : = <1, 0, 0, …>; V = <1, 0, 0, 0, …> V = <1, 1, 0, 0, …> V = <1, 2, 1, 0, …> V = <1, 3, 3, 1, …> Loop n times V : = V + SHIFT(V); V = nth row of Pascal’s triangle

Example: V : = <1, 0, 0, …>; PV : = 1; Loop n times V : = V + SHIFT(V); PV : = PV(1+X); V = nth row of Pascal’s triangle

Example: V : = <1, 0, 0, …>; Loop n times V : = V + SHIFT(V); PV = (1+ X)n V = nth row of Pascal’s triangle As expected, the coefficients of PV give the nth row of Pascal’s triangle

To summarize… Given a sequence V = < a 0, a 1, a 2, . . . , an, … > associate a formal power series with it P(X) = a i. X i i=0 This is the “generating function” for V

Fibonaccis F 0 = 0, F 1 = 1, Fn = Fn-1 + Fn-2 i. e. , the sequence <0, 1, 1, 2, 3, 5, 8, 13…> is represented by the power series 0 + 1 X 1 + 1 X 2 + 2 X 3 + 3 X 4 + 5 X 5 + 8 X 6 +…

Two Representations F 0 = 0, F 1 = 1, Fn = Fn-1 + Fn-2 A(X) = 0 + 1 X 1 + 1 X 2 + 2 X 3 + 3 X 4 + 5 X 5 + 8 X 6 +… Can we write A(X) more succinctly?
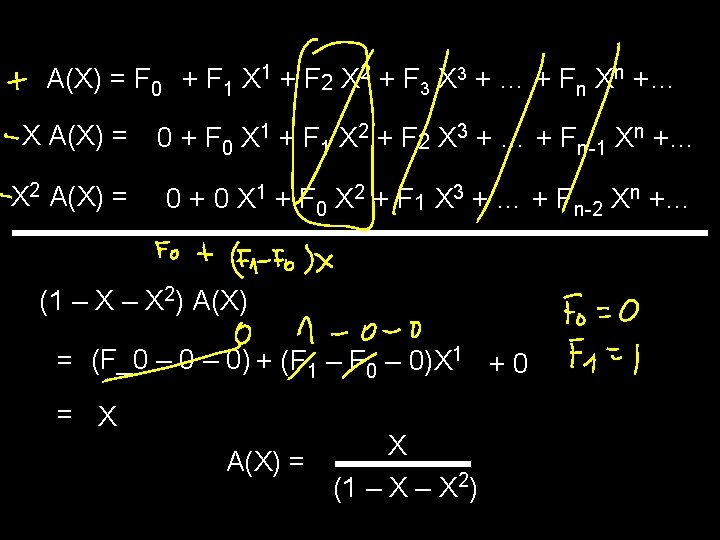
A(X) = F 0 + F 1 X 1 + F 2 X 2 + F 3 X 3 + … + Fn Xn +… X A(X) = 0 + F 0 X 1 + F 1 X 2 + F 2 X 3 + … + Fn-1 Xn +… X 2 A(X) = 0 + 0 X 1 + F 0 X 2 + F 1 X 3 + … + Fn-2 Xn +… (1 – X 2) A(X) = (F_0 – 0) + (F 1 – F 0 – 0)X 1 + 0 = X X A(X) = (1 – X 2)

Fibonaccis F 0 = 0, F 1 = 1, Fn = Fn-1 + Fn-2 has the generating function X A(X) = (1 – X 2) i. e. , the coefficient of Xn in A(X) is Fn

X + X 2 + 2 X 3 + 3 X 4 + 5 X 5 + 8 X 6 1 – X 2 X -(X – X 2 – X 3) X 2 + X 3 -(X 2 – X 3 – X 4) 2 X 3 + X 4 -(2 X 3 – 2 X 4 – 2 X 5) 3 X 4 + 2 X 5 -(3 X 4 – 3 X 5 – 3 X 6) 5 X 5 + 3 X 6 -(5 X 5 – 5 X 6 – 5 X 7) 8 X 6 + 5 X 7 -(8 X 6 – 8 X 7 – 8 X 8)

Two representations of the same thing… F 0 = 0, F 1 = 1, Fn = Fn-1 + Fn-2 X A(X) = (1 – X 2)

Closed form? F 0 = 0, F 1 = 1, Fn = Fn-1 + Fn-2 X A(X) = (1 – X 2) let’s factor (1 – X – X 2) = (1 - φX)(1 – (-1/φ)X) where φ = 1 + √ 5 2

Simplify, simplify… F 0 = 0, F 1 = 1, Fn = Fn-1 + Fn-2 X A(X) = (1 - φX)(1 – (-1/φ)X) some elementary algebra omitted…* 1 1 1 -1 A(X) = + √ 5 (1 - φX) √ 5 (1 – (-1/φ)X) *you are not allowed to say this in your answers…

1 1 1 -1 A(X) = + √ 5 (1 - φX) √ 5 (1 – (-1/φ)X) 1 (1 - φX) = 1 + φ X + φ2 X 2 + … + φn X n + … 1 = 1 + Y 2 + Y 3 + … + Y n + … 1 -Y the Infinite Geometric Series


Closed form for Fibonaccis Fn = 1 φn -1 (-1/φ)n + √ 5 where φ = 1 + √ 5 2 “golden ratio” Abraham de Moivre (1730) Leonhard Euler (1765) J. P. M. Binet (1843)

Closed form for Fibonaccis Fn = 1 φn -1 (-1/φ)n + √ 5 1 φn closest integer to √ 5
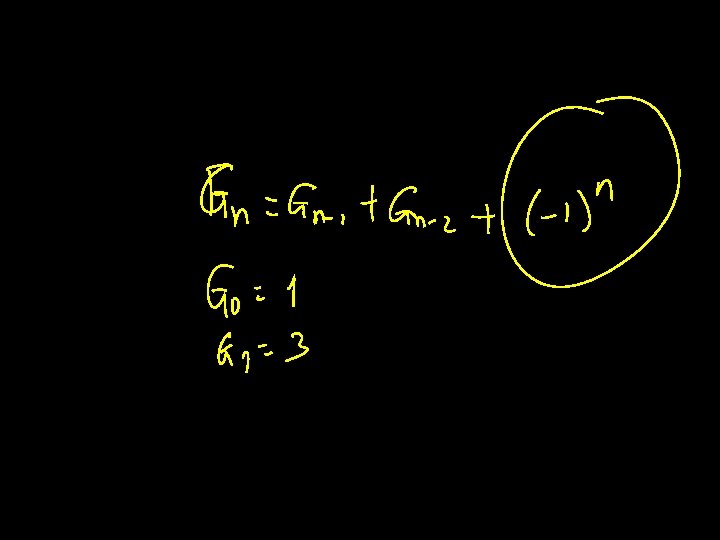

To recap… Given a sequence V = < a 0, a 1, a 2, . . . , an, … > associate a formal power series with it P(X) = a i. X i i=0 This is the “generating function” for V We just used this for the Fibonaccis…

Multiplication A(X) = a 0 + a 1 X + a 2 X 2 + … B(X) = b 0 + b 1 X + b 2 X 2 + … multiply them together (A*B)(X) = (a 0*b 0) + (a 0 b 1 + a 1 b 0) X + (a 0 b 2 + a 1 b 1 + a 2 b 0) X 2 + (a 0 b 3 + a 1 b 2 + a 2 b 1 + a 3 b 0 ) X 2 +… seems a bit less natural in the vector representation (it’s called a “convolution” there)

Mult. : special case A(X) = a 0 + a 1 X + a 2 X 2 + … 1 2 Special case: B(X) = 1 + X + … = 1 -X multiply them together (A*B)(X) = a 0 + (a 0 + a 1) X + (a 0 + a 1 + a 2) X 2 + (a 0 + a 1 + a 2 + a 3) X 2 + … it gives us partial sums!

For example… Suppose A(X) = 1 + X 2 + … = 1 1 -X and B(X) = 1 + X 2 + … = 1 1 -X then (A*B)(X) = 1 + 2 X + 3 X 2 + 4 X 3 + … 1 1 = * 1 -X 1 = (1 -X)2 Generating function for the sequence <0, 1, 2, 3, 4…>

What happens if we again take prefix sums? Take 1 + 2 X + 3 X 2 + 4 X 3 + … = 1 (1 -X)2 multiplying through by 1/(1 -X) ¢ 1 + ¢ 2 X 1 + ¢ 3 X 2 + ¢ 4 X 3 +… 1 = (1 -X)3 Generating function for the triangular numbers!



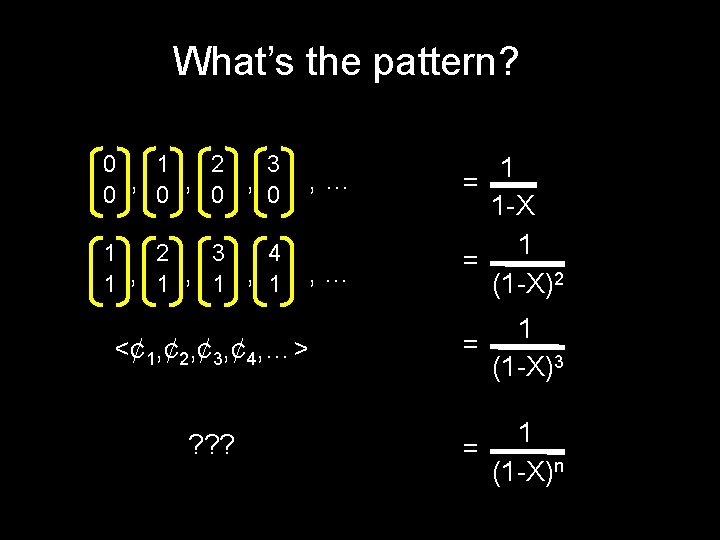
What’s the pattern? 1 3 0 2 , , , 0 0 , … 1 2 4 3 1 , 1 , … 1 1 -X 1 = (1 -X)2 = <¢ 1, ¢ 2, ¢ 3, ¢ 4, …> 1 = (1 -X)3 ? ? ? 1 = (1 -X)n

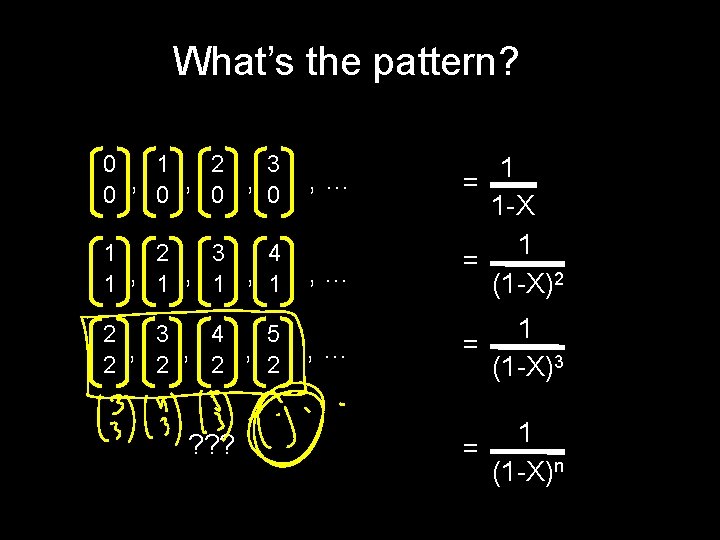
What’s the pattern? 1 3 0 2 , , , 0 0 , … 1 2 4 3 1 , 1 , … 2 3 4 5 , , , 2 2 ? ? ? , … 1 1 -X 1 = (1 -X)2 = 1 = (1 -X)3 1 = (1 -X)n

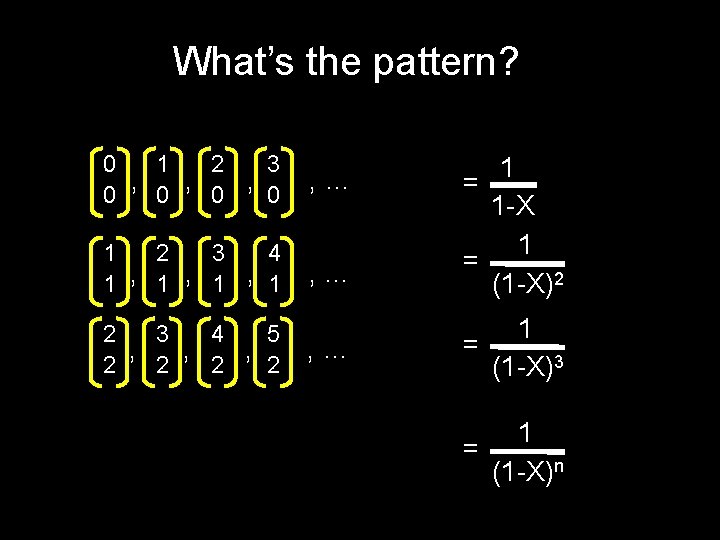
What’s the pattern? 1 3 0 2 , , , 0 0 , … 1 2 4 3 1 , 1 , … 2 3 4 5 , , , 2 2 , … 1 1 -X 1 = (1 -X)2 = 1 = (1 -X)3 1 = (1 -X)n

What’s the pattern? 1 3 0 2 , , , 0 0 , … 1 2 4 3 1 , 1 , … 2 3 4 5 , , , 2 2 , … 1 1 -X 1 = (1 -X)2 = 1 = (1 -X)3 k=0 k+n-1 Xk 1 = (1 -X)n

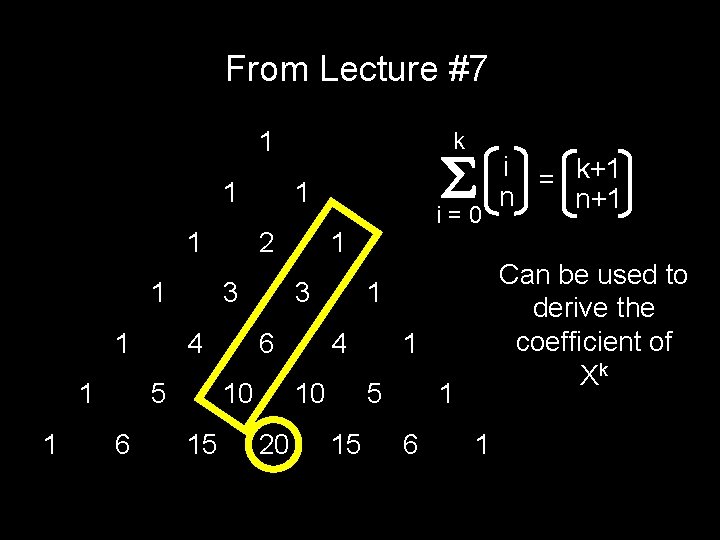
From Lecture #7 1 1 1 1 6 2 4 6 4 1 5 15 1 6 i = k+1 n n+1 Can be used to derive the coefficient of Xk 1 10 20 i=0 1 3 10 15 1 3 5 k 1

What’s the pattern? k=0 k+n-1 Xk 1 = (1 -X)n

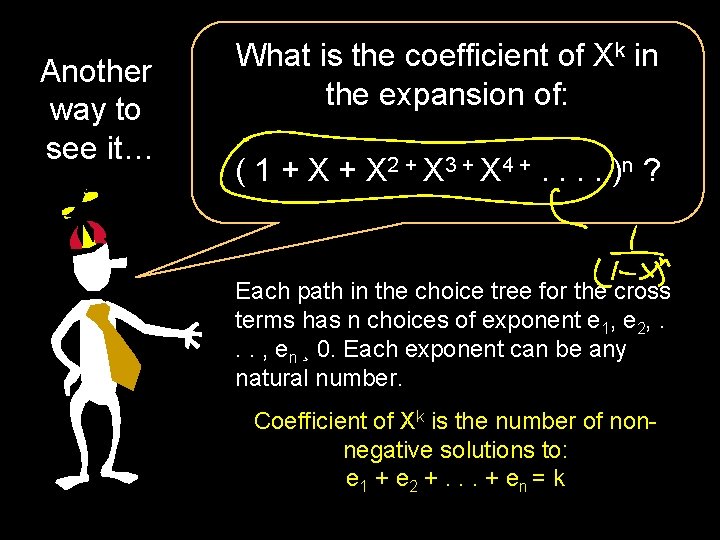
Another way to see it… What is the coefficient of Xk in the expansion of: ( 1 + X 2 + X 3 + X 4 +. . ) n ? Each path in the choice tree for the cross terms has n choices of exponent e 1, e 2, . . . , en ¸ 0. Each exponent can be any natural number. Coefficient of Xk is the number of nonnegative solutions to: e 1 + e 2 +. . . + e n = k
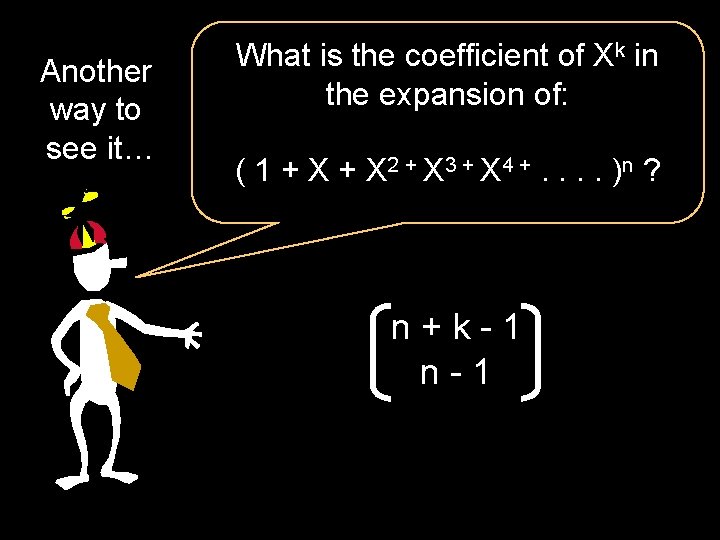
Another way to see it… What is the coefficient of Xk in the expansion of: ( 1 + X 2 + X 3 + X 4 +. . ) n ? n+k-1 n-1

Recap: getting partial sums A(X) = a 0 + a 1 X + a 2 X 2 + … A(X) a 0 + (a 0 + a 1) X = + (a 0 + a 1 + a 2) X 2 1 -X + (a 0 + a 1 + a 2 + a 3) X 2 + … dividing by (1 -X) gives us partial sums!

Here’s an interesting use… k+2 2 k=0 (k+2)(k+1) 2 subtract off Xk = 1 (1 -X)3 3/2 1 and add ½ 2 (1 -X) 1 -X k=0 k 2 2 Xk X(1+X) = 2(1 -X)3

From the previous page… k=0 k 2 Xk X(1+X) = (1 -X)3 hence if we take partial sums… k=0 sum of first Xk = X(1+X) * 1 1 -X (1 -X)3 k squares
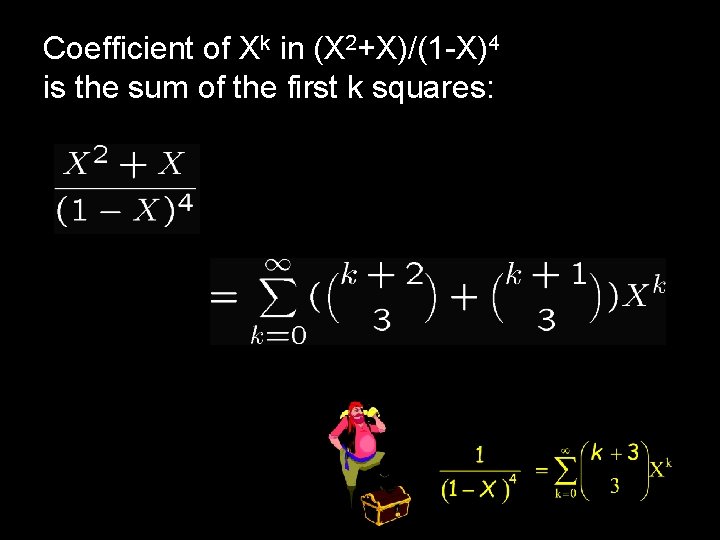
Coefficient of Xk in (X 2+X)/(1 -X)4 is the sum of the first k squares:
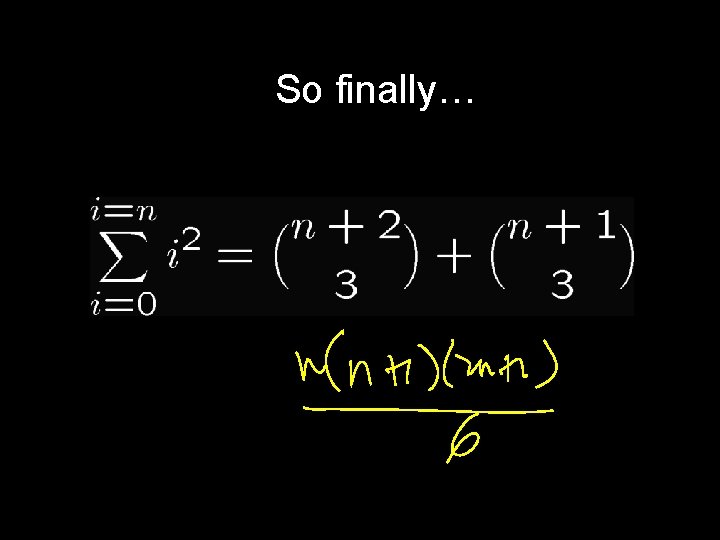
So finally…

Finally, a different counting problem…

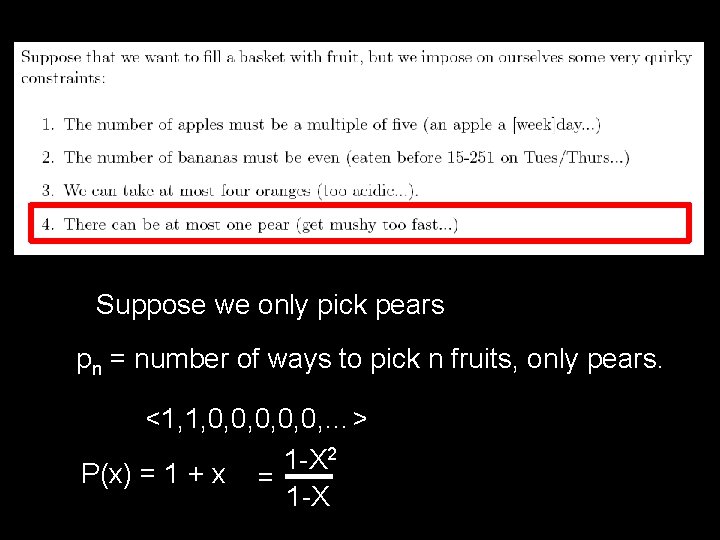
Let cn = number of ways to pick exactly n fruits. E. g. , c 5 = 6 What is a closed form for cn?

Recall Multiplication A(X) = a 0 + a 1 X + a 2 X 2 + … B(X) = b 0 + b 1 X + b 2 X 2 + … multiply them together (A*B)(X) = (a 0*b 0) + (a 0 b 1 + a 1 b 0) X + (a 0 b 2 + a 1 b 1 + a 2 b 0) X 2 + (a 0 b 3 + a 1 b 2 + a 2 b 1 + a 3 b 0 ) X 2 +…

So if A(x), B(x), O(x) and P(x) are the generating functions for the number of ways to fill baskets using only one kind of fruit the generating function for number of ways to fill basket using any of these fruit is given by C(x) = A(x)B(x)O(x)P(x)

Suppose we only pick bananas bn = number of ways to pick n fruits, only bananas. <1, 0, …> B(x) = 1 + x 2 + x 4 + x 6 +… 1 = 1 -X 2

Suppose we only pick apples an = number of ways to pick n fruits, only apples. <1, 0, 0, 1, …> A(x) = 1 + x 5 + x 10 + x 15 1 +… = 1 -X 5

Suppose we only pick oranges on = number of ways to pick n fruits, only oranges. <1, 1, 1, 0, 0, 0, …> O(x) = 1 + x 2 + x 3 + x 4 1 -X 5 = 1 -X

Suppose we only pick pears pn = number of ways to pick n fruits, only pears. <1, 1, 0, 0, 0, …> 1 -X 2 P(x) = 1 + x = 1 -X

Let cn = number of ways to pick exactly n fruits of any type cn xn = A(x) B(x) O(x) P(x) 5 1 -X 2 1 1 1 -X = 1 -X 5 1 -X 2 1 -X 1 = (1 -X)2

Let cn = number of ways to pick exactly n fruits of any type cn is coefficient of Xn in cn = n+1. 1 (1 -X)2 <1, 2, 3, 4, …>

More operations: Differentiation A(X) = a 0 + a 1 X + a 2 X 2 + … differentiate it… A’(X) = a 1 + 2 a 2 X + 3 a 3 X 2 … A’(X) = (i+1)ai+1 Xi iai Xi i=0 X A’(X) = i=0

Formal Power Series Basic operations on Formal Power Series Writing the generating function for a recurrence binomial and multinomial coefficients Solving G. F. to get closed form G. F. s for common sequences Here’s What Prefix sums using G. F. s You Need to Know… Using G. F. s to solve counting problems
 Great theoretical ideas in computer science
Great theoretical ideas in computer science Great ideas in theoretical computer science
Great ideas in theoretical computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science 15 251
15 251 Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Great theoretical ideas in computer science
Great theoretical ideas in computer science Cse 111
Cse 111 Graph theory in computer science
Graph theory in computer science 8 ideas of computer architecture
8 ideas of computer architecture Cs 61
Cs 61 8 great ideas in computer architecture
8 great ideas in computer architecture 8 great ideas in computer architecture
8 great ideas in computer architecture 15-251
15-251 Em nada ponho a minha fé numero
Em nada ponho a minha fé numero Stanford cs 251
Stanford cs 251 Half lap muff coupling drawing
Half lap muff coupling drawing Legge 251 2000
Legge 251 2000 Stanford cs 251
Stanford cs 251 Aecp army
Aecp army Cs251
Cs251 Aae 251
Aae 251 Cs 251
Cs 251 15-251
15-251 Describe your favourite subject
Describe your favourite subject Ideas have consequences bad ideas have victims
Ideas have consequences bad ideas have victims Que es una idea principal
Que es una idea principal China big idea
China big idea Science national honor society project ideas
Science national honor society project ideas National children's science congress projects ideas
National children's science congress projects ideas Turning great strategy into great performance
Turning great strategy into great performance Great faces great places
Great faces great places Egoistic leadership
Egoistic leadership Great white shark versus hammerhead shark
Great white shark versus hammerhead shark Did alexander the great deserve to be called great
Did alexander the great deserve to be called great Enlightened despot catherine
Enlightened despot catherine With great expectations comes great responsibility
With great expectations comes great responsibility A great deal vs a great many
A great deal vs a great many With great power comes great responsibility batman
With great power comes great responsibility batman Does alexander deserve to be called the great
Does alexander deserve to be called the great No shadow of turning
No shadow of turning Great explorations in math and science
Great explorations in math and science Social science vs natural science
Social science vs natural science Brances of science
Brances of science Natural and physical science
Natural and physical science Applied science vs pure science
Applied science vs pure science Natural science and social science similarities
Natural science and social science similarities Science fusion digital lessons
Science fusion digital lessons Tragedy of the commons
Tragedy of the commons Windcube
Windcube Hard science and soft science
Hard science and soft science Wjec gcse computer science
Wjec gcse computer science University of phoenix computer science
University of phoenix computer science How many fields in computer science
How many fields in computer science What is procedural abstraction
What is procedural abstraction Unsolved problems in computer science
Unsolved problems in computer science University of bridgeport engineering
University of bridgeport engineering