15 213 The course that gives CMU its




























- Slides: 40

15 -213 “The course that gives CMU its Zip!” Integers Sep 3, 2002 Topics n Numeric Encodings l Unsigned & Two’s complement n Programming Implications l C promotion rules n Basic operations l Addition, negation, multiplication n Programming Implications l Consequences of overflow l Using shifts to perform power-of-2 multiply/divide class 03. ppt 15 -213 F’ 02

C Puzzles n n n Taken from old exams Assume machine with 32 bit word size, two’s complement integers For each of the following C expressions, either: l Argue that is true for all argument values l Give example where not true • x < 0 Initialization ((x*2) < 0) • ux >= 0 • x & 7 == 7 (x<<30) < 0 int x = foo(); • ux > -1 int y = bar(); • x > y unsigned ux = x; • x * x >= 0 unsigned uy = y; • x > 0 && y > 0 x + y > 0 – 2– -x < -y • x >= 0 -x <= 0 • x <= 0 -x >= 0 15 -213, F’ 02

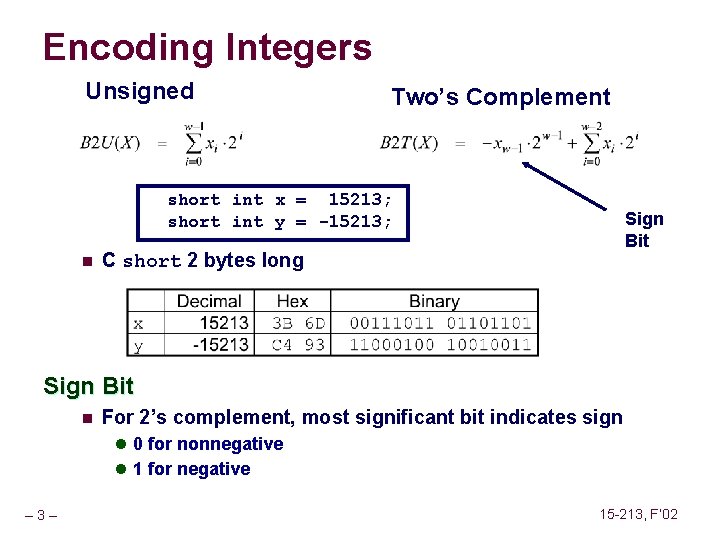
Encoding Integers Unsigned Two’s Complement short int x = 15213; short int y = -15213; n Sign Bit C short 2 bytes long Sign Bit n For 2’s complement, most significant bit indicates sign l 0 for nonnegative l 1 for negative – 3– 15 -213, F’ 02

Encoding Example (Cont. ) x = y = – 4– 15213: 00111011 01101101 -15213: 11000100 10010011 15 -213, F’ 02

Numeric Ranges Unsigned Values n UMin = 0 Two’s Complement Values n TMin = – 2 w– 1 000… 0 n UMax 100… 0 = 2 w – 1 111… 1 n TMax = 2 w– 1 011… 1 Other Values n Minus 1 Values for W = 16 – 5– 111… 1 15 -213, F’ 02

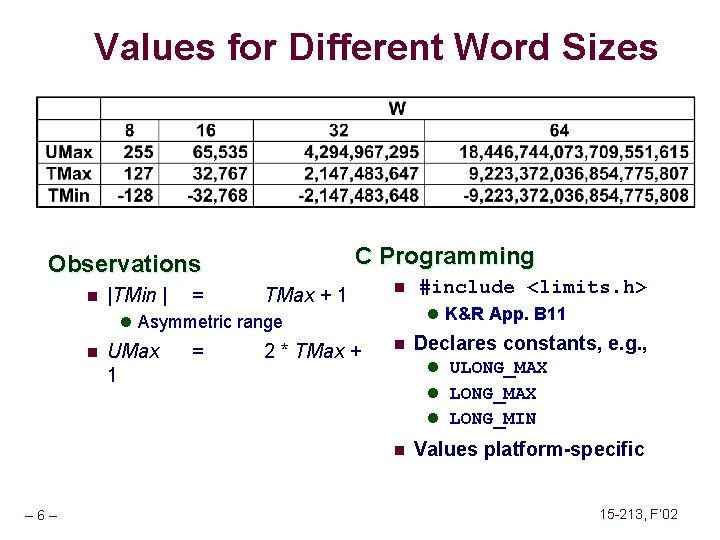
Values for Different Word Sizes C Programming Observations n |TMin | = TMax + 1 n l K&R App. B 11 l Asymmetric range n UMax 1 = 2 * TMax + #include <limits. h> n Declares constants, e. g. , l ULONG_MAX l LONG_MIN n – 6– Values platform-specific 15 -213, F’ 02

Unsigned & Signed Numeric Values X 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 – 7– B 2 U(X) 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 B 2 T(X) 0 1 2 3 4 5 6 7 – 8 – 7 – 6 – 5 – 4 – 3 – 2 – 1 Equivalence n Same encodings for nonnegative values Uniqueness n n Every bit pattern represents unique integer value Each representable integer has unique bit encoding Can Invert Mappings n U 2 B(x) = B 2 U-1(x) l Bit pattern for unsigned integer n T 2 B(x) = B 2 T-1(x) l Bit pattern for two’s comp integer 15 -213, F’ 02

Casting Signed to Unsigned C Allows Conversions from Signed to Unsigned short int x = 15213; unsigned short int ux = (unsigned short) x; short int y = -15213; unsigned short int uy = (unsigned short) y; Resulting Value n n No change in bit representation Nonnegative values unchanged l ux = 15213 n Negative values change into (large) positive values l uy = 50323 – 8– 15 -213, F’ 02

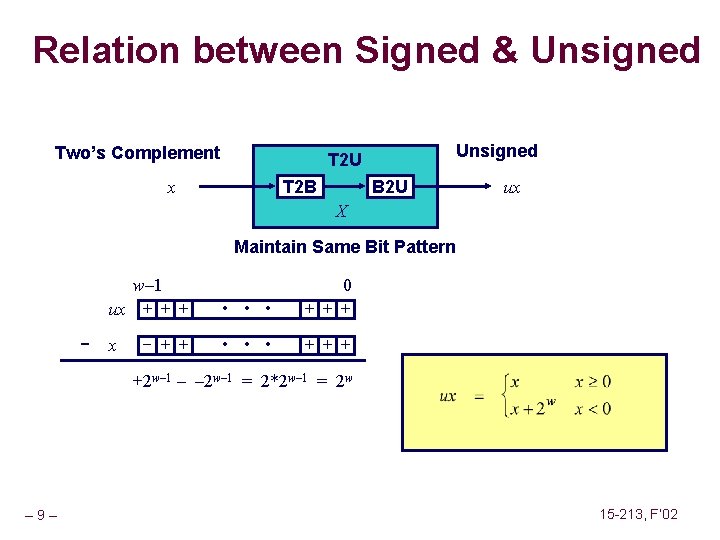
Relation between Signed & Unsigned Two’s Complement Unsigned T 2 U T 2 B x B 2 U ux X Maintain Same Bit Pattern - w– 1 ux + + + • • • 0 + ++ x • • • + ++ - ++ +2 w– 1 – – 2 w– 1 = 2*2 w– 1 = 2 w – 9– 15 -213, F’ 02

Relation Between Signed & Unsigned n – 10 – uy = y + 2 * 32768 = y + 65536 15 -213, F’ 02

Signed vs. Unsigned in C Constants n By default are considered to be signed integers n Unsigned if have “U” as suffix 0 U, 4294967259 U Casting n Explicit casting between signed & unsigned same as U 2 T and T 2 U int tx, ty; unsigned ux, uy; tx = (int) ux; uy = (unsigned) ty; n Implicit casting also occurs via assignments and procedure calls tx = ux; uy = ty; – 11 – 15 -213, F’ 02

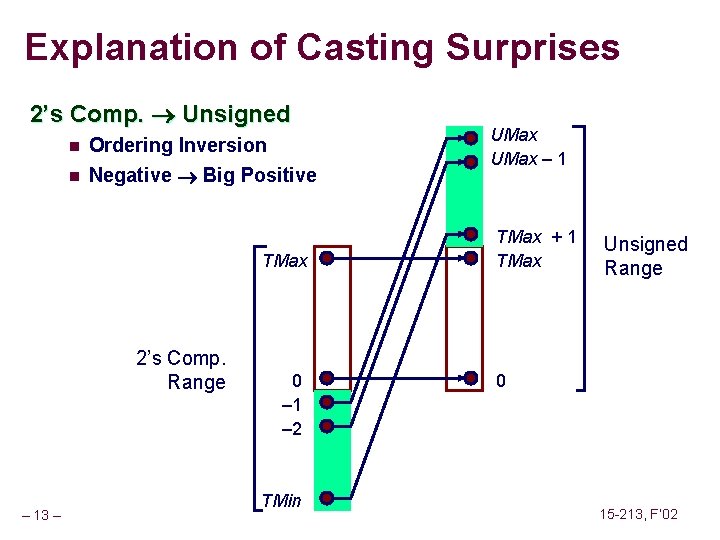
Casting Surprises Expression Evaluation n If mix unsigned and signed in single expression, signed values implicitly cast to unsigned n Including comparison operations <, >, ==, <=, >= n Examples for W = 32 Constant 1 Constant 2 0 0 U -1 0 U 2147483647 – 12 – Relation 0 U 0 0 U -2147483648 2147483647 U -2147483648 -1 -2 -2 (unsigned) -1 -2 -2 2147483647 2147483648 U 2147483647 (int) 2147483648 U Evaluation == < > > unsigned < > > < > unsigned 15 -213, F’ 02 signed

Explanation of Casting Surprises 2’s Comp. Unsigned n Ordering Inversion n Negative Big Positive TMax 2’s Comp. Range – 13 – 0 – 1 – 2 TMin UMax – 1 TMax + 1 TMax Unsigned Range 0 15 -213, F’ 02

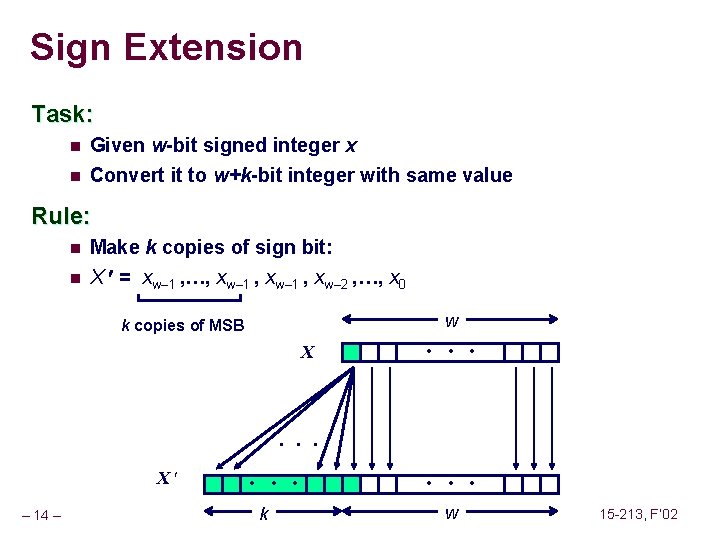
Sign Extension Task: n Given w-bit signed integer x n Convert it to w+k-bit integer with same value Rule: n n Make k copies of sign bit: X = xw– 1 , …, xw– 1 , xw– 2 , …, x 0 w k copies of MSB X • • • X – 14 – • • • k • • • w 15 -213, F’ 02

Sign Extension Example short int x = 15213; int ix = (int) x; short int y = -15213; int iy = (int) y; Decimal Hex 3 B 6 D 15213 00 00 3 B 6 D C 4 93 -15213 FF FF C 4 93 x ix y iy n n – 15 – Binary 00111011 01101101 00000000 00111011 01101101 11000100 10010011 11111111 11000100 10010011 Converting from smaller to larger integer data type C automatically performs sign extension 15 -213, F’ 02

Justification For Sign Extension Prove Correctness by Induction on k n Induction Step: extending by single bit maintains value w X X - • • • - + • • • w+1 n n Key observation: – 2 w– 1 = – 2 w +2 w– 1 Look at weight of upper bits: X X – 16 – – 2 w– 1 xw– 1 – 2 w xw– 1 + 2 w– 1 xw– 1 = – 2 w– 1 xw– 1 15 -213, F’ 02

Why Should I Use Unsigned? Don’t Use Just Because Number Nonzero n C compilers on some machines generate less efficient code unsigned i; for (i = 1; i < cnt; i++) a[i] += a[i-1]; n Easy to make mistakes for (i = cnt-2; i >= 0; i--) a[i] += a[i+1]; Do Use When Performing Modular Arithmetic n n Multiprecision arithmetic Other esoteric stuff Do Use When Need Extra Bit’s Worth of Range n – 17 – Working right up to limit of word size 15 -213, F’ 02

Negating with Complement & Increment Claim: Following Holds for 2’s Complement ~x + 1 == -x Complement n Observation: ~x + x == 1111… 112 == -1 x 1001 110 1 + ~x 0110 001 0 -1 111 1 Increment n n ~x + (-x + 1) ~x + 1 == -x == -1 + (-x + 1) Warning: Be cautious treating int’s as integers – 18 – n OK here 15 -213, F’ 02

Comp. & Incr. Examples x = 15213 0 – 19 – 15 -213, F’ 02

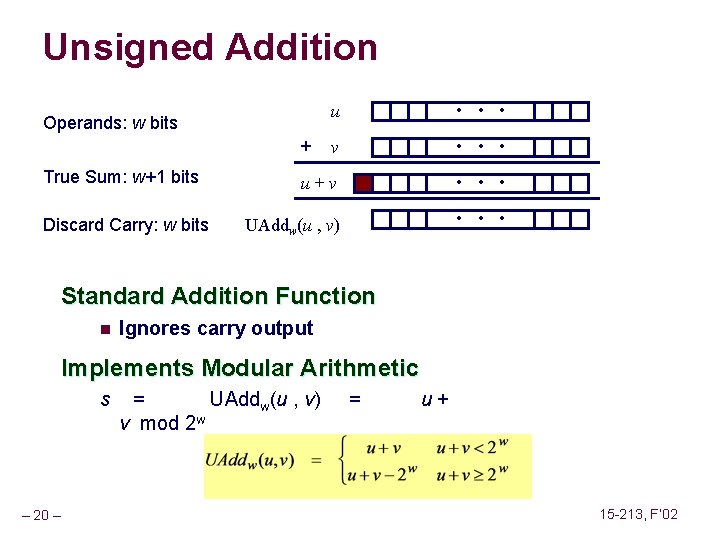
Unsigned Addition u • • • v • • • u+v • • • UAddw(u , v) • • • Operands: w bits + True Sum: w+1 bits Discard Carry: w bits Standard Addition Function n Ignores carry output Implements Modular Arithmetic s – 20 – = UAddw(u , v) v mod 2 w = u+ 15 -213, F’ 02

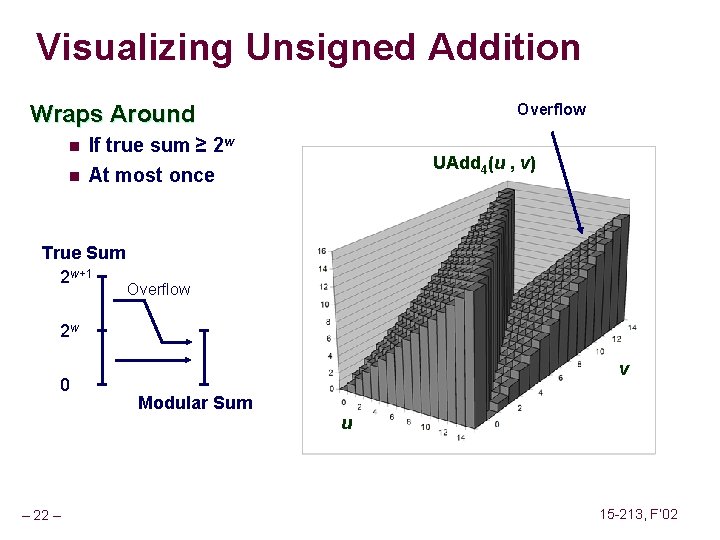
Visualizing Integer Addition Add 4(u , v) Integer Addition n 4 -bit integers u, v n Compute true sum Add 4(u , v) Values increase linearly with u and v Forms planar surface n n v u – 21 – 15 -213, F’ 02

Visualizing Unsigned Addition Wraps Around n If true sum ≥ 2 w n At most once True Sum 2 w+1 Overflow UAdd 4(u , v) Overflow 2 w 0 – 22 – v Modular Sum u 15 -213, F’ 02

Mathematical Properties Modular Addition Forms an Abelian Group n Closed under addition 0 UAddw(u , v) 2 w – 1 n Commutative UAddw(u , v) = UAddw(v , u) n Associative UAddw(t, UAddw(u , v)) = UAddw(t, u ), v) n 0 is additive identity UAddw(u , 0) = u n Every element has additive inverse l Let UCompw (u ) = 2 w – u UAddw(u , UCompw (u )) = 0 – 23 – 15 -213, F’ 02

Two’s Complement Addition u • • • v • • • u+v • • • TAddw(u , v) • • • Operands: w bits + True Sum: w+1 bits Discard Carry: w bits TAdd and UAdd have Identical Bit-Level Behavior n n – 24 – Signed vs. unsigned addition in C: int s, t, u, v; s = (int) ((unsigned) u + (unsigned) v); t = u + v Will give s == t 15 -213, F’ 02

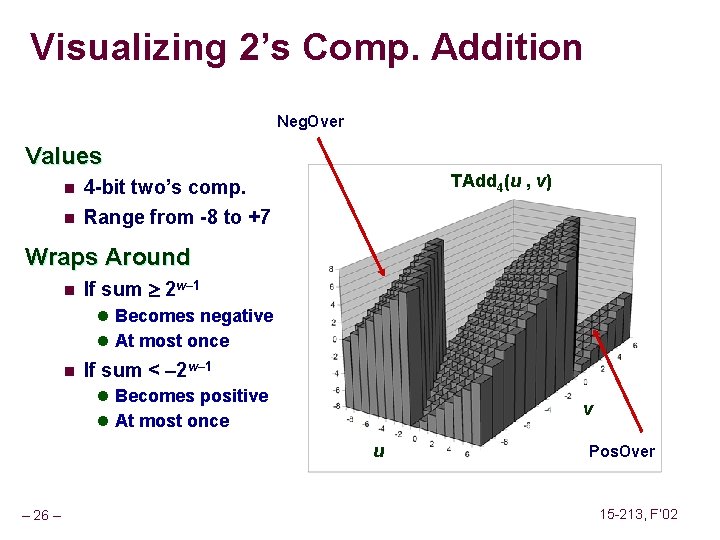
Characterizing TAdd Functionality n n n True sum requires w+1 bits Drop off MSB Treat remaining bits as 2’s comp. integer Pos. Over True Sum 0 111… 1 Pos. Over TAdd Result 0 100… 0 2 w – 1 011… 1 0 000… 0 1 100… 0 – 2 w – 1 1 000… 0 – 2 w TAdd(u , v) >0 v <0 2 w– 1 100… 0 Neg. Over (Neg. Over) <0 u >0 (Pos. Over) Neg. Over – 25 – 15 -213, F’ 02

Visualizing 2’s Comp. Addition Neg. Over Values n 4 -bit two’s comp. n Range from -8 to +7 TAdd 4(u , v) Wraps Around n If sum 2 w– 1 l Becomes negative l At most once n If sum < – 2 w– 1 l Becomes positive v l At most once u – 26 – Pos. Over 15 -213, F’ 02

Detecting 2’s Comp. Overflow Task 2 w– 1 n Given s = TAddw(u , v) n Determine if s = Addw(u , v) Example int s, u, v; s = u + v; n Pos. Over 2 w – 1 0 Claim n Overflow iff either: Neg. Over u, v < 0, s 0 (Neg. Over) u, v 0, s < 0 (Pos. Over) ovf = (u<0 == v<0) && (u<0 != s<0); – 27 – 15 -213, F’ 02

Mathematical Properties of TAdd Isomorphic Algebra to UAdd n TAddw(u , v) = U 2 T(UAddw(T 2 U(u ), T 2 U(v))) l Since both have identical bit patterns Two’s Complement Under TAdd Forms a Group n n Closed, Commutative, Associative, 0 is additive identity Every element has additive inverse Let TCompw (u ) = U 2 T(UCompw(T 2 U(u )) TAddw(u , TCompw (u )) = 0 – 28 – 15 -213, F’ 02

Multiplication Computing Exact Product of w-bit numbers x, y n Either signed or unsigned Ranges n Unsigned: 0 ≤ x * y ≤ (2 w – 1) 2 = 22 w – 2 w+1 + 1 l Up to 2 w bits n Two’s complement min: x * y ≥ (– 2 w– 1)*(2 w– 1– 1) = – 22 w– 2 + 2 w– 1 l Up to 2 w– 1 bits n Two’s complement max: x * y ≤ (– 2 w– 1) 2 = 22 w– 2 l Up to 2 w bits, but only for (TMinw)2 Maintaining Exact Results n n – 29 – Would need to keep expanding word size with each product computed Done in software by “arbitrary precision” arithmetic packages 15 -213, F’ 02

Unsigned Multiplication in C Operands: w bits * True Product: 2*w bits u · v u • • • v • • • UMultw(u , v) Discard w bits: w bits • • • Standard Multiplication Function n Ignores high order w bits Implements Modular Arithmetic UMultw(u , v) 2 w – 30 – = u · v mod 15 -213, F’ 02

Unsigned vs. Signed Multiplication Unsigned Multiplication unsigned ux = (unsigned) x; unsigned uy = (unsigned) y; unsigned up = ux * uy n n Truncates product to w-bit number up = UMultw(ux, uy) Modular arithmetic: up = ux uy mod 2 w Two’s Complement Multiplication int x, y; int p = x * y; n n – 31 – Compute exact product of two w-bit numbers x, y Truncate result to w-bit number p = TMultw(x, y) 15 -213, F’ 02

Unsigned vs. Signed Multiplication Unsigned Multiplication unsigned ux = (unsigned) x; unsigned uy = (unsigned) y; unsigned up = ux * uy Two’s Complement Multiplication int x, y; int p = x * y; Relation n n – 32 – Signed multiplication gives same bit-level result as unsigned up == (unsigned) p 15 -213, F’ 02

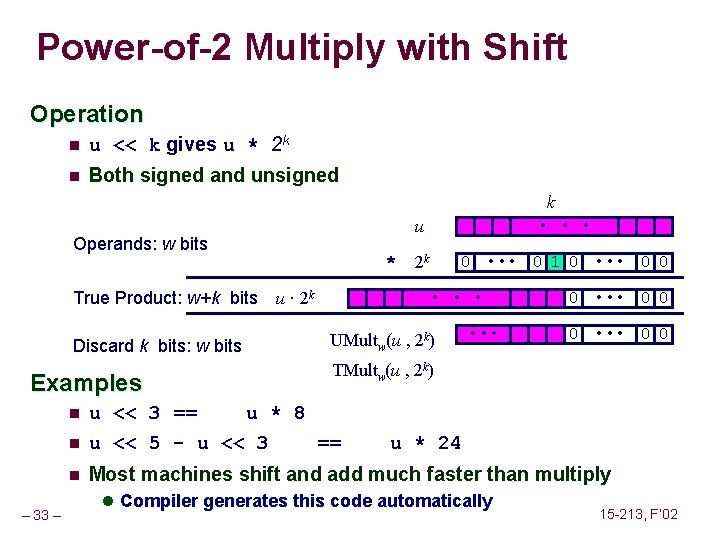
Power-of-2 Multiply with Shift Operation n u << k gives u * 2 k n Both signed and unsigned Operands: w bits True Product: w+k bits Discard k bits: w bits Examples u · 2 k 2 k 0 • • • 0 1 0 • • • 0 0 • • • UMultw(u , 2 k) • • • 0 • • • 0 0 TMultw(u , 2 k) n u << 3 == u * 8 u << 5 - u << 3 == n Most machines shift and add much faster than multiply n – 33 – * u k • • • u * 24 l Compiler generates this code automatically 15 -213, F’ 02

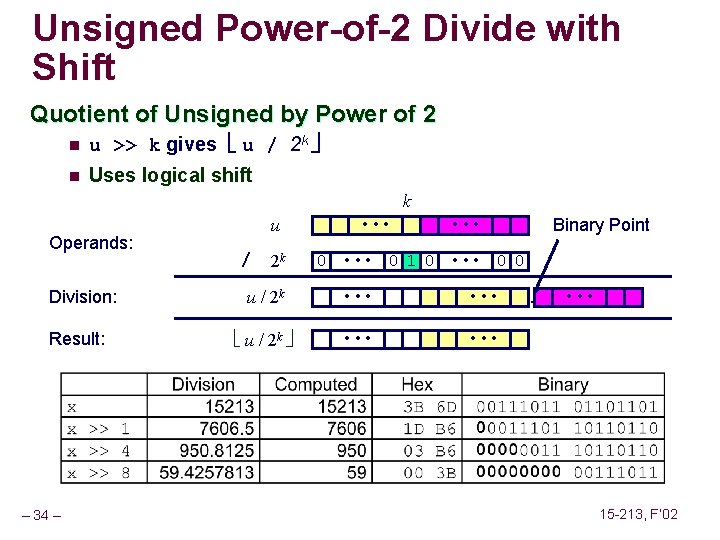
Unsigned Power-of-2 Divide with Shift Quotient of Unsigned by Power of 2 n u >> k gives u / 2 k n Uses logical shift k Operands: Division: Result: – 34 – u / 2 k • • • Binary Point • • • 0 • • • 0 1 0 • • • 0 0 u / 2 k 0 • • • u / 2 k 0 • • • 15 -213, F’ 02

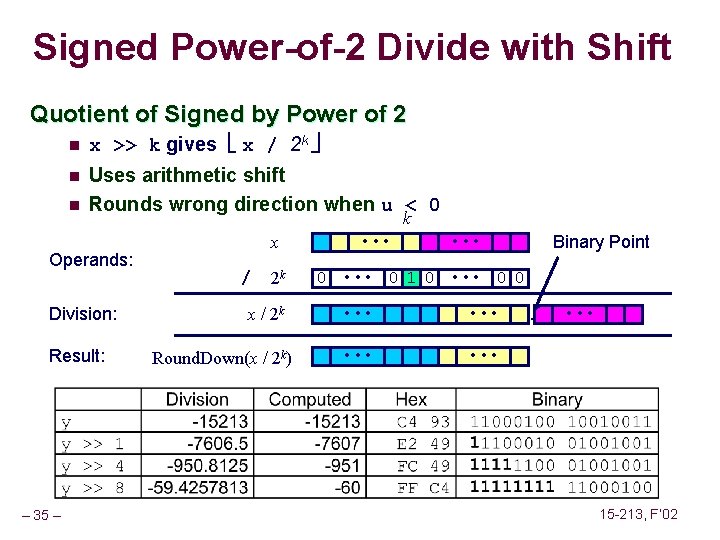
Signed Power-of-2 Divide with Shift Quotient of Signed by Power of 2 n x >> k gives x / 2 k n Uses arithmetic shift Rounds wrong direction when u < 0 n Operands: Division: Result: – 35 – k x / 2 k Round. Down(x / 2 k) • • • Binary Point • • • 0 • • • 0 1 0 • • • 0 0 0 • • • 15 -213, F’ 02

Correct Power-of-2 Divide Quotient of Negative Number by Power of 2 n n Want x / 2 k (Round Toward 0) Compute as (x+2 k-1)/ 2 k l In C: (x + (1<<k)-1) >> k l Biases dividend toward 0 Case 1: No rounding Dividend: k u +2 k +– 1 1 / 2 k u / 2 k 0 • • • 0 0 1 • • • 1 1 1 Divisor: • • • 1 • • • 1 1 Binary Point 0 • • • 0 1 0 • • • 0 0 0 • • • 1 1 • • • . 1 • • • 1 1 Biasing has no effect – 36 – 15 -213, F’ 02

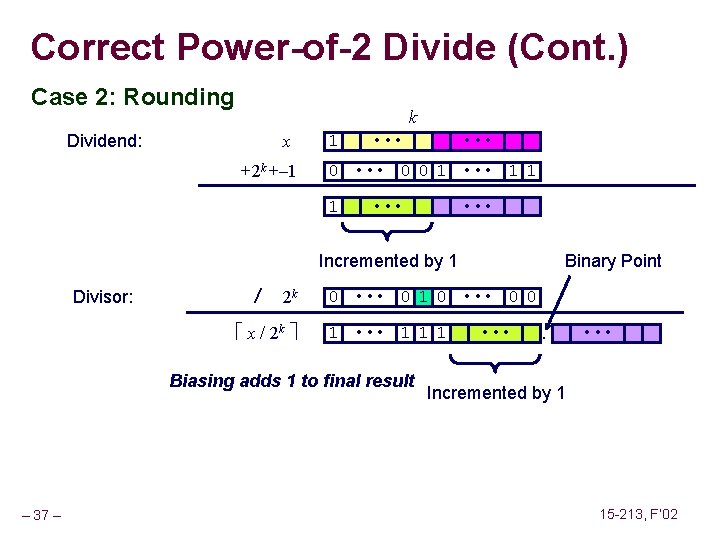
Correct Power-of-2 Divide (Cont. ) Case 2: Rounding k Dividend: x +2 k +– 1 1 • • • 0 • • • 0 0 1 • • • 1 1 1 • • • Incremented by 1 Divisor: / 2 k x / 2 k 0 • • • 0 1 0 • • • 0 0 0 • • • 1 1 Biasing adds 1 to final result – 37 – Binary Point • • • Incremented by 1 15 -213, F’ 02

Properties of Unsigned Arithmetic Unsigned Multiplication with Addition Forms Commutative Ring n n Addition is commutative group Closed under multiplication 0 UMultw(u , v) 2 w – 1 n Multiplication Commutative UMultw(u , v) = UMultw(v , u) n Multiplication is Associative UMultw(t, UMultw(u , v)) = UMultw(t, u ), v) n 1 is multiplicative identity UMultw(u , 1) = u n Multiplication distributes over addtion UMultw(t, UAddw(u , v)) = UAddw(UMultw(t, u ), UMultw(t, v)) – 38 – 15 -213, F’ 02

Properties of Two’s Comp. Arithmetic Isomorphic Algebras n Unsigned multiplication and addition l Truncating to w bits n Two’s complement multiplication and addition l Truncating to w bits Both Form Rings n Isomorphic to ring of integers mod 2 w Comparison to Integer Arithmetic n n Both are rings Integers obey ordering properties, e. g. , u > 0, v > 0 n – 39 – u + v > v u · v > 0 These properties are not obeyed by two’s comp. arithmetic TMax + 1 == 15213 * 30426 == TMin -10030 (16 -bit words) 15 -213, F’ 02

C Puzzle Answers n n Assume machine with 32 bit word size, two’s comp. integers TMin makes a good counterexample in many cases x < 0 q ux >= 0 q x & 7 == 7 q ux > -1 q x > y q x * x >= 0 q x > 0 && y > 0 x + y > 0 False: TMax, TMax q x >= 0 -x <= 0 True: q x <= 0 -x >= 0 False: TMin – 40 – ((x*2) < 0) False: TMin q True: (x<<30) < 0 0 = UMin True: x 1 = 1 False: 0 -x < -y False: -1, TMin False: 30426 –TMax < 0 15 -213, F’ 02
 213 cmu
213 cmu 18-213 cmu
18-213 cmu 18-213 cmu
18-213 cmu Cmu 213
Cmu 213 Cmu 213
Cmu 213 18-213 cmu
18-213 cmu Cmu 15-213
Cmu 15-213 15-213 cmu
15-213 cmu Block av độ 2
Block av độ 2 Tìm vết của đường thẳng
Tìm vết của đường thẳng Thể thơ truyền thống
Thể thơ truyền thống Tôn thất thuyết là ai
Tôn thất thuyết là ai Hãy nói thật ít để làm được nhiều
Hãy nói thật ít để làm được nhiều Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Gây tê cơ vuông thắt lưng
Gây tê cơ vuông thắt lưng Ngoại tâm thu thất chùm đôi
Ngoại tâm thu thất chùm đôi Walmart thất bại ở nhật
Walmart thất bại ở nhật Sau thất bại ở hồ điển triệt
Sau thất bại ở hồ điển triệt Cmu machine learning
Cmu machine learning The skeleton gives the body its basic shape
The skeleton gives the body its basic shape Course number and title
Course number and title Chaine parallèle muscle
Chaine parallèle muscle English bond t junction elevation
English bond t junction elevation Ct-213
Ct-213 15 213
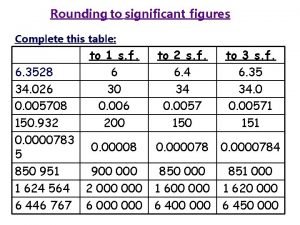
15 213 Significant figures
Significant figures Ct 213
Ct 213 Ee 213
Ee 213 213 table
213 table Cs213
Cs213 Outline 213
Outline 213 Administration definition
Administration definition 15 213
15 213 Zva-213-s+
Zva-213-s+ Ct 213
Ct 213 15-213 introduction to computer systems
15-213 introduction to computer systems Outline 213
Outline 213 Ceng 213
Ceng 213 Outline 213
Outline 213 Ct 213
Ct 213 Ct 213
Ct 213