15 213 Floating Point Arithmetic August 31 2009

15 -213 Floating Point Arithmetic August 31, 2009 Topics n n class 03. ppt IEEE Floating Point Standard Rounding Floating Point Operations Mathematical properties

Floating Point Puzzles n For each of the following C expressions, either: l Argue that it is true for all argument values l Explain why not true • x == (int)(float) x int x = …; • x == (int)(double) x float f = …; • f == (float)(double) f double d = …; • d == (float) d • f == -(-f); Assume neither d nor f is Na. N • 2/3 == 2/3. 0 • d < 0. 0 ((d*2) < 0. 0) • d > f -f > -d • d * d >= 0. 0 • (d+f)-d == f – 2 – 15 -213: Intro to Computer Systems Fall 2009 ©

IEEE Floating Point IEEE Standard 754 n Established in 1985 as uniform standard for floating point arithmetic l Before that, many idiosyncratic formats n Supported by all major CPUs Driven by Numerical Concerns n n Nice standards for rounding, overflow, underflow Hard to make go fast l Numerical analysts predominated over hardware types in defining standard – 3 – 15 -213: Intro to Computer Systems Fall 2009 ©

Fractional Binary Numbers 2 i 2 i– 1 4 2 1 bi bi– 1 • • • b 2 b 1 b 0. b– 1 b– 2 b– 3 1/2 1/4 1/8 • • • b–j • • • 2–j Representation – 4 – n Bits to right of “binary point” represent fractional powers of 2 n Represents rational number: 15 -213: Intro to Computer Systems Fall 2009 ©

Frac. Binary Number Examples Value 5 -3/4 2 -7/8 63/64 Representation 101. 112 10. 1112 0. 1111112 Observations Divide by 2 by shifting right n Multiply by 2 by shifting left n Numbers of form 0. 111111… 2 just below 1. 0 n l 1/2 + 1/4 + 1/8 + … + 1/2 i + … 1. 0 l Use notation 1. 0 – – 5 – 15 -213: Intro to Computer Systems Fall 2009 ©

Representable Numbers Limitation Can only exactly represent numbers of the form x/2 k n Other numbers have repeating bit representations n Value 1/3 1/5 1/10 – 6 – Representation 0. 010101[01]… 2 0. 00110011[0011]… 2 0. 000110011[0011]… 2 15 -213: Intro to Computer Systems Fall 2009 ©

Floating Point Representation Numerical Form n – 1 s M 2 E l Sign bit s determines whether number is negative or positive l Significand M normally a fractional value in range [1. 0, 2. 0). l Exponent E weights value by power of two Encoding s exp frac MSB is sign bit n exp field encodes E n frac field encodes M n – 7 – 15 -213: Intro to Computer Systems Fall 2009 ©

Floating Point Precisions Encoding s exp frac MSB is sign bit n exp field encodes E n frac field encodes M n Sizes n Single precision: 8 exp bits, 23 frac bits l 32 bits total n Double precision: 11 exp bits, 52 frac bits l 64 bits total n Extended precision: 15 exp bits, 63 frac bits l Only found in Intel-compatible machines l Stored in 80 bits » 1 bit wasted – 8 – 15 -213: Intro to Computer Systems Fall 2009 ©

“Normalized” Numeric Values Condition n exp 000… 0 and exp 111… 1 Exponent coded as biased value E = Exp – Bias l Exp : unsigned value denoted by exp l Bias : Bias value » Single precision: 127 (Exp: 1… 254, E: -126… 127) » Double precision: 1023 (Exp: 1… 2046, E: -1022… 1023) » in general: Bias = 2 e-1 - 1, where e is number of exponent bits Significand coded with implied leading 1 M = 1. xxx…x 2 l xxx…x: bits of frac l Minimum when 000… 0 (M = 1. 0) l Maximum when 111… 1 (M = 2. 0 – ) l Get extra leading bit for “free” – 9 – 15 -213: Intro to Computer Systems Fall 2009 ©

Normalized Encoding Example Value Float F = 15213. 0; n 1521310 = 111011012 = 1. 11011012 X 213 Significand M = frac = 1. 11011012 1101101000002 Exponent E = Bias = Exp = 13 127 140 = 100011002 Floating Point Representation: Hex: Binary: 140: 15213: – 10 – 4 6 6 D B 4 0 0 0100 0110 1101 1011 0100 0000 100 0110 0 1110 1101 1011 01 15 -213: Intro to Computer Systems Fall 2009 ©

Denormalized Values Condition n exp = 000… 0 Value n n Exponent value E = –Bias + 1 Significand value M = 0. xxx…x 2 l xxx…x: bits of frac Cases n exp = 000… 0, frac = 000… 0 l Represents value 0 l Note that have distinct values +0 and – 0 n exp = 000… 0, frac 000… 0 l Numbers very close to 0. 0 l Lose precision as get smaller – 11 – l “Gradual underflow” 15 -213: Intro to Computer Systems Fall 2009 ©

Special Values Condition n exp = 111… 1 Cases n exp = 111… 1, frac = 000… 0 l Represents value (infinity) l Operation that overflows l Both positive and negative l E. g. , 1. 0/0. 0 = 1. 0/ 0. 0 = + , 1. 0/ 0. 0 = n exp = 111… 1, frac 000… 0 l Not-a-Number (Na. N) l Represents case when no numeric value can be determined l E. g. , sqrt(– 1), , * 0 – 12 – 15 -213: Intro to Computer Systems Fall 2009 ©

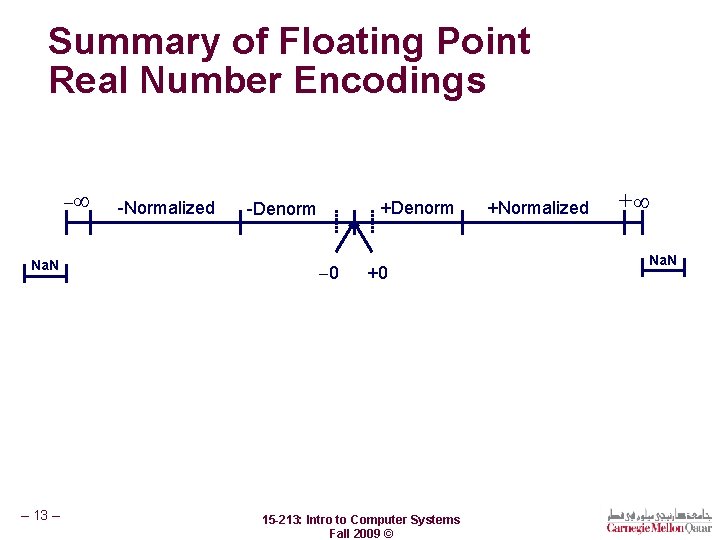
Summary of Floating Point Real Number Encodings Na. N – 13 – -Normalized +Denorm -Denorm 0 +0 15 -213: Intro to Computer Systems Fall 2009 © +Normalized + Na. N

Tiny Floating Point Example 8 -bit Floating Point Representation n the sign bit is in the most significant bit. n the next four bits are the exponent, with a bias of 7. the last three bits are the frac n l Same General Form as IEEE Format n n normalized, denormalized representation of 0, Na. N, infinity 7 6 s – 14 – 0 3 2 exp frac 15 -213: Intro to Computer Systems Fall 2009 ©

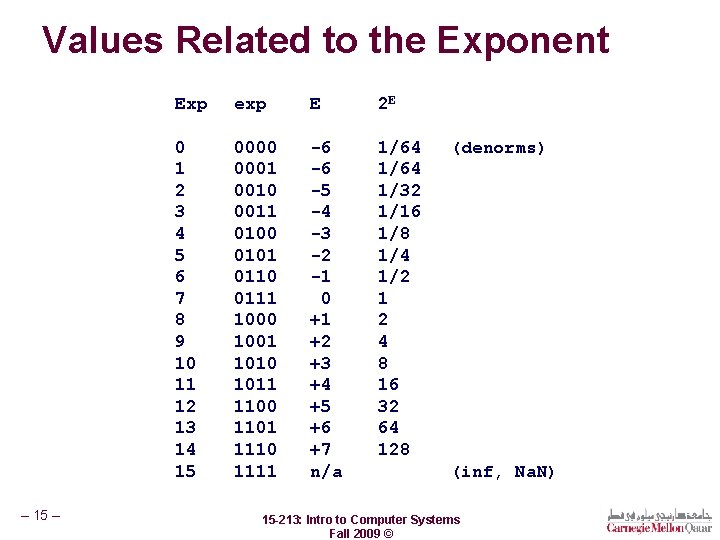
Values Related to the Exponent – 15 – Exp exp E 2 E 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111 -6 -6 -5 -4 -3 -2 -1 0 +1 +2 +3 +4 +5 +6 +7 n/a 1/64 1/32 1/16 1/8 1/4 1/2 1 2 4 8 16 32 64 128 (denorms) (inf, Na. N) 15 -213: Intro to Computer Systems Fall 2009 ©

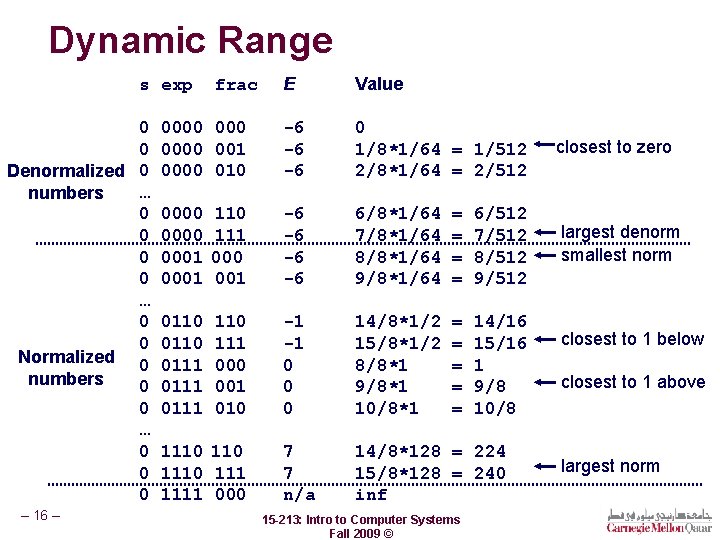
Dynamic Range E Value 0000 001 0000 010 -6 -6 -6 0 1/8*1/64 = 1/512 2/8*1/64 = 2/512 closest to zero 0000 0001 110 111 000 001 -6 -6 6/8*1/64 7/8*1/64 8/8*1/64 9/8*1/64 = = 6/512 7/512 8/512 9/512 largest denorm smallest norm 0110 0111 110 111 000 001 010 -1 -1 0 0 0 14/8*1/2 15/8*1/2 8/8*1 9/8*1 10/8*1 = = = 14/16 15/16 1 9/8 10/8 7 7 n/a 14/8*128 = 224 15/8*128 = 240 inf s exp 0 0 Denormalized 0 … numbers 0 0 … 0 0 Normalized 0 numbers 0 0 … 0 0 0 – 16 – frac 1110 1111 000 15 -213: Intro to Computer Systems Fall 2009 © closest to 1 below closest to 1 above largest norm

Distribution of Values 6 -bit IEEE-like format n e = 3 exponent bits n f = 2 fraction bits Bias is 3 n Notice how the distribution gets denser toward zero. – 17 – 15 -213: Intro to Computer Systems Fall 2009 ©

Distribution of Values (close-up view) 6 -bit IEEE-like format n e = 3 exponent bits n f = 2 fraction bits Bias is 3 n – 18 – 15 -213: Intro to Computer Systems Fall 2009 ©

Interesting Numbers Description exp Zero 00… 00 0. 0 Smallest Pos. Denorm. 00… 00 00… 01 2– {23, 52} X 2– {126, 1022} frac Numeric Value Single 1. 4 X 10– 45 n Double 4. 9 X 10– 324 n Largest Denormalized 00… 00 11… 11 (1. 0 – ) X 2– {126, 1022} Single 1. 18 X 10– 38 n Double 2. 2 X 10– 308 n Smallest Pos. Normalized 00… 01 00… 00 n 1. 0 X 2– {126, 1022} Just larger than largest denormalized One 01… 11 00… 00 1. 0 Largest Normalized 11… 10 11… 11 (2. 0 – ) X 2{127, 1023} Single 3. 4 X 1038 n Double 1. 8 X 10308 n – 19 – 15 -213: Intro to Computer Systems Fall 2009 ©

Special Properties of Encoding FP Zero Same as Integer Zero n All bits = 0 Can (Almost) Use Unsigned Integer Comparison n Must first compare sign bits Must consider -0 = 0 Na. Ns problematic l Will be greater than any other values l What should comparison yield? n Otherwise OK l Denorm vs. normalized l Normalized vs. infinity – 20 – 15 -213: Intro to Computer Systems Fall 2009 ©

Floating Point Operations Conceptual View n First compute exact result n Make it fit into desired precision l Possibly overflow if exponent too large l Possibly round to fit into frac Rounding Modes (illustrate with $ rounding) Zero n Round down (- ) n Round up (+ ) n Nearest Even (default) n $1. 40 $1. 60 $1. 50 $2. 50 –$1. 50 $1 $1 $2 $1 $1 $1 $2 $2 $3 $2 –$1 –$2 Note: 1. Round down: rounded result is close to but no greater than true result. 2. Round up: rounded result is close to but no less than true result. – 21 – 15 -213: Intro to Computer Systems Fall 2009 ©

Closer Look at Round-To-Even Default Rounding Mode n Hard to get any other kind without dropping into assembly n All others are statistically biased l Sum of set of positive numbers will consistently be over- or under- estimated Applying to Other Decimal Places / Bit Positions n When exactly halfway between two possible values l Round so that least significant digit is even n E. g. , round to nearest hundredth 1. 2349999 1. 2350001 1. 2350000 1. 2450000 – 22 – 1. 23 1. 24 (Less than half way) (Greater than half way) (Half way—round up) (Half way—round down) 15 -213: Intro to Computer Systems Fall 2009 ©

Rounding Binary Numbers Binary Fractional Numbers “Even” when least significant bit is 0 n Half way when bits to right of rounding position = 100… 2 n Examples Round to nearest 1/4 (2 bits right of binary point) Value Binary Rounded Action Rounded Value 2 3/32 10. 000112 10. 002 (<1/2—down) 2 2 3/16 10. 001102 10. 012 (>1/2—up) 2 1/4 2 7/8 10. 111002 11. 002 (1/2—up) 3 2 5/8 10. 101002 10. 102 (1/2—down) 2 1/2 n – 23 – 15 -213: Intro to Computer Systems Fall 2009 ©

FP Multiplication Operands (– 1)s 1 M 1 2 E 1 * (– 1)s 2 M 2 2 E 2 Exact Result (– 1)s M 2 E n n n Sign s: s 1 ^ s 2 Significand M: M 1 * M 2 Exponent E: E 1 + E 2 Fixing n If M ≥ 2, shift M right, increment E n If E out of range, overflow Round M to fit frac precision n Implementation n – 24 – Biggest chore is multiplying significands 15 -213: Intro to Computer Systems Fall 2009 ©

FP Addition Operands (– 1)s 1 M 1 2 E 1 (– 1)s 2 M 2 2 E 2 n E 1–E 2 (– 1)s 1 M 1 Assume E 1 > E 2 Exact Result (– 1)s M 2 E n (– 1)s 2 M 2 + Sign s, significand M: l Result of signed align & add n Exponent E: E 1 Fixing n If M ≥ 2, shift M right, increment E n if M < 1, shift M left k positions, decrement E by k Overflow if E out of range Round M to fit frac precision n – 25 – n 15 -213: Intro to Computer Systems Fall 2009 ©

Mathematical Properties of FP Add Compare to those of Abelian Group n Closed under addition? YES l But may generate infinity or Na. N Commutative? n Associative? YES NO n l Overflow and inexactness of rounding 0 is additive identity? YES n Every element has additive inverse ALMOST n l Except for infinities & Na. Ns Monotonicity n a ≥ b a+c ≥ b+c? ALMOST l Except for infinities & Na. Ns – 26 – 15 -213: Intro to Computer Systems Fall 2009 ©

Math. Properties of FP Mult Compare to Commutative Ring n Closed under multiplication? YES l But may generate infinity or Na. N Multiplication Commutative? n Multiplication is Associative? n YES NO l Possibility of overflow, inexactness of rounding 1 is multiplicative identity? YES n Multiplication distributes over addition? NO n l Possibility of overflow, inexactness of rounding Monotonicity n a ≥ b & c ≥ 0 a *c ≥ b *c? l Except for infinities & Na. Ns – 27 – 15 -213: Intro to Computer Systems Fall 2009 © ALMOST

Creating Floating Point Number Steps 7 6 n Normalize to have leading 1 n Round to fit within fraction Postnormalize to deal with effects of rounding n s 0 3 2 exp frac Case Study n n – 28 – Convert 8 -bit unsigned numbers to tiny floating point format Example Numbers 128 10000000 15 00001101 33 0001 35 00010011 138 10001010 63 00111111 15 -213: Intro to Computer Systems Fall 2009 ©

Normalize 7 6 s 0 3 2 exp frac Requirement n Set binary point so that numbers of form 1. xxxxx n Adjust all to have leading one l Decrement exponent as shift left Value 128 15 17 19 138 63 – 29 – Binary 100000001101 00010011 10001010 00111111 Fraction 1. 0000000 1. 1010000 1. 0001000 1. 0011000 1. 0001010 1. 1111100 15 -213: Intro to Computer Systems Fall 2009 © Exponent 7 3 5 5 7 5

Rounding 1. BBGRXXX Guard bit: LSB of result Sticky bit: OR of remaining bits Round bit: 1 st bit removed Round up conditions n n Round = 1, Sticky = 1 > 0. 5 Guard = 1, Round = 1, Sticky = 0 Round to even Value 128 15 17 19 138 63 – 30 – Fraction 1. 0000000 1. 1010000 1. 0001000 1. 0011000 1. 0001010 1. 1111100 GRS 000 100 010 111 111 Incr? Rounded N 1. 000 N 1. 101 N 1. 000 Y 1. 010 Y 1. 001 Y 10. 000 15 -213: Intro to Computer Systems Fall 2009 ©

Postnormalize Issue – 31 – n Rounding may have caused overflow n Handle by shifting right once & incrementing exponent Value Rounded Exp Adjusted Result 128 1. 000 7 128 15 1. 101 3 15 17 1. 000 4 16 19 1. 010 4 20 138 1. 001 7 134 63 10. 000 5 1. 000/6 64 15 -213: Intro to Computer Systems Fall 2009 ©

Floating Point in C C Guarantees Two Levels float double single precision double precision Conversions n n Casting between int, float, and double changes numeric values Double or float to int l Truncates fractional part l Like rounding toward zero l Not defined when out of range or Na. N » Generally sets to TMin n int to double l Exact conversion, as long as int has ≤ 53 bit word size n int to float l Will round according to rounding mode – 32 – 15 -213: Intro to Computer Systems Fall 2009 ©

Curious Excel Behavior n Spreadsheets use floating point for all computations Some imprecision for decimal arithmetic n Can yield nonintuitive results to an accountant! n – 33 – 15 -213: Intro to Computer Systems Fall 2009 ©

Summary IEEE Floating Point Has Clear Mathematical Properties n Represents numbers of form M X 2 E n Can reason about operations independent of implementation l As if computed with perfect precision and then rounded n Not the same as real arithmetic l Violates associativity/distributivity l Makes life difficult for compilers & serious numerical applications programmers – 34 – 15 -213: Intro to Computer Systems Fall 2009 ©