15 082 J and 6 855 J Successive

15. 082 J and 6. 855 J Successive Shortest Path Algorithm

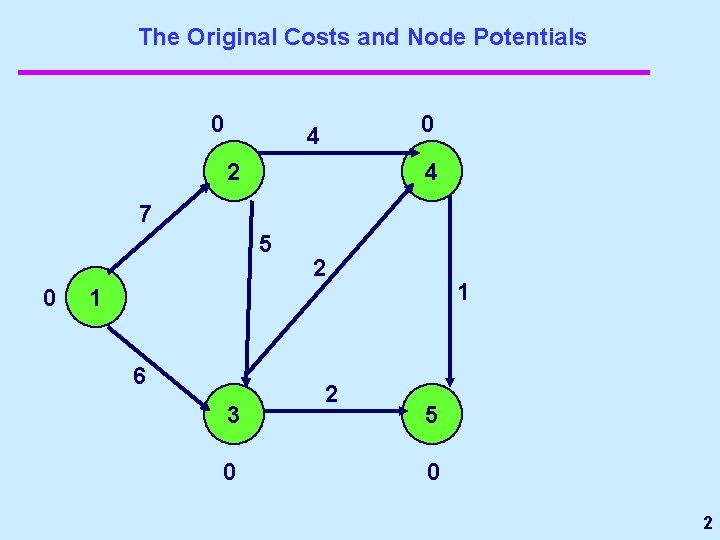
The Original Costs and Node Potentials 0 0 4 2 4 7 5 0 2 1 1 6 3 0 2 5 0 2

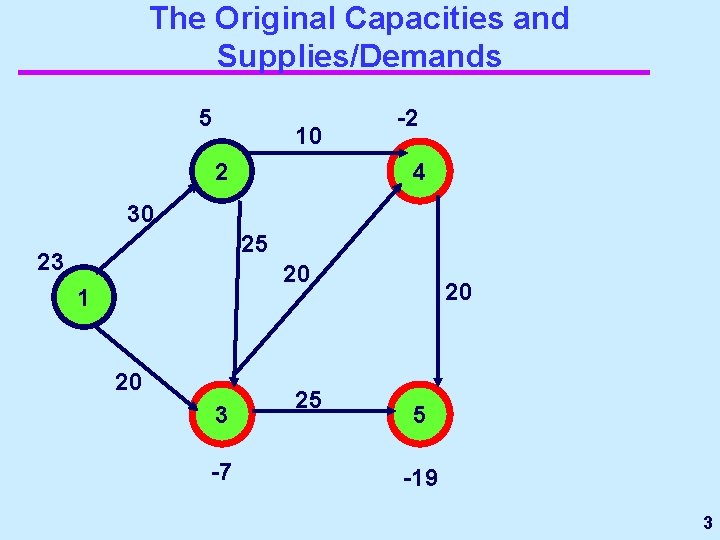
The Original Capacities and Supplies/Demands 5 10 2 -2 4 30 25 23 20 1 20 3 -7 25 20 5 -19 3

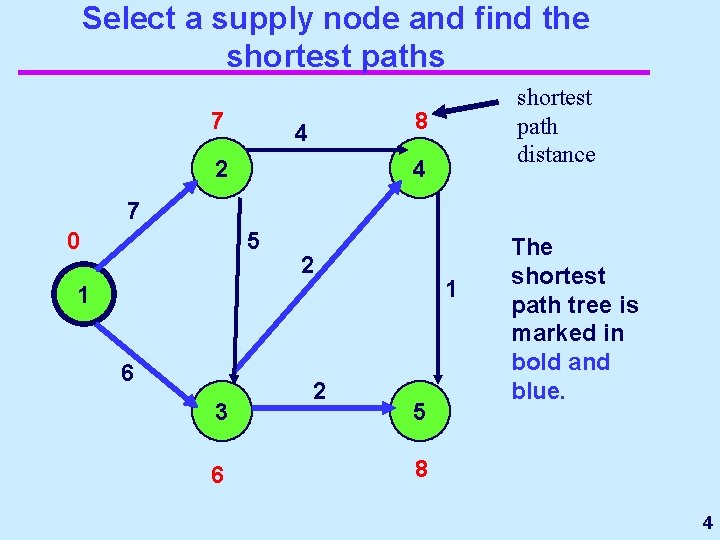
Select a supply node and find the shortest paths 7 shortest path distance 8 4 2 4 7 0 5 2 1 1 6 3 6 2 5 The shortest path tree is marked in bold and blue. 8 4

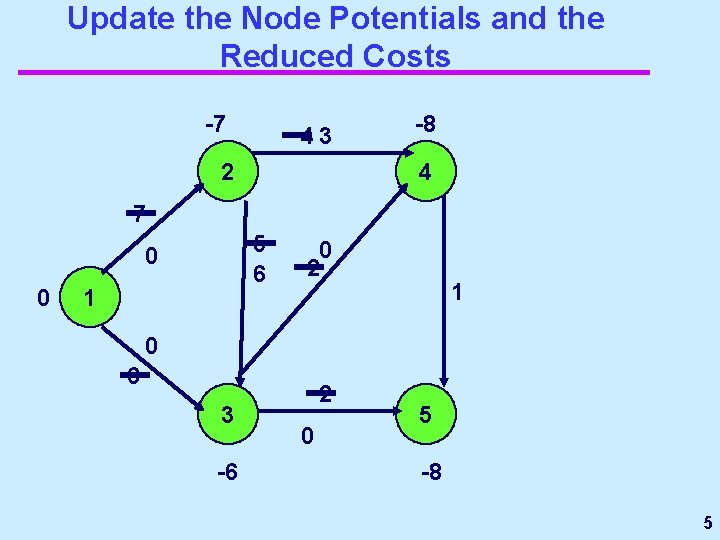
Update the Node Potentials and the Reduced Costs -7 43 2 -8 4 7 5 6 0 0 1 0 2 1 0 6 3 -6 2 0 5 -8 5

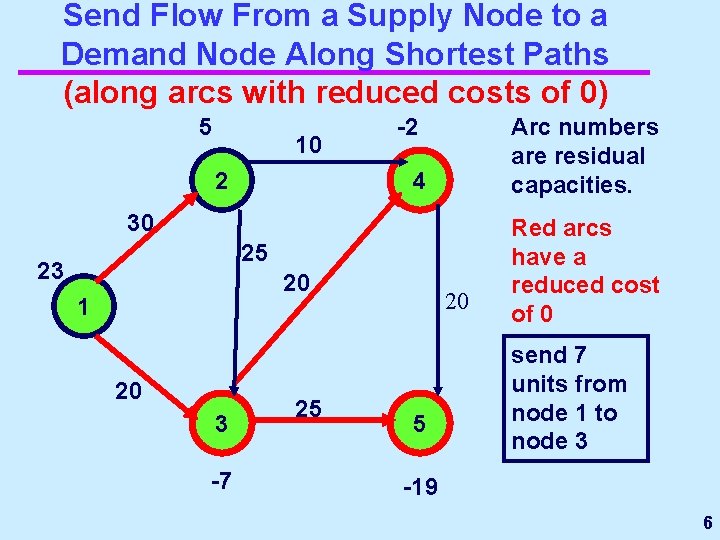
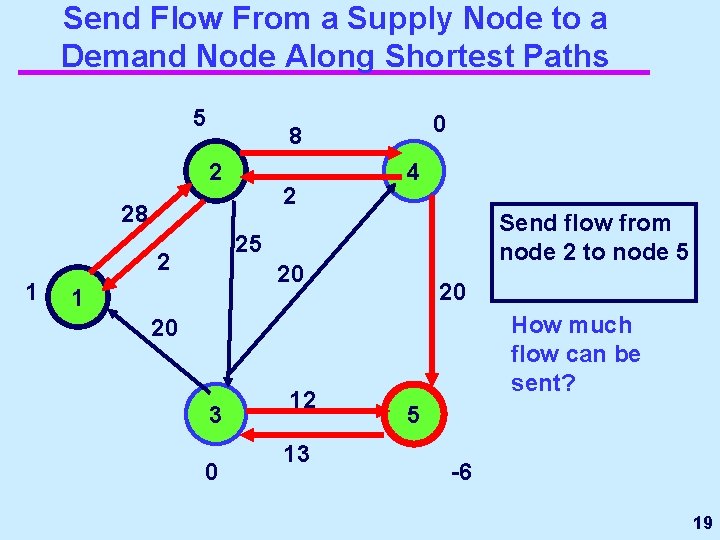
Send Flow From a Supply Node to a Demand Node Along Shortest Paths (along arcs with reduced costs of 0) 5 10 2 -2 Arc numbers are residual capacities. 4 30 25 23 20 1 20 3 -7 25 20 5 Red arcs have a reduced cost of 0 send 7 units from node 1 to node 3 -19 6

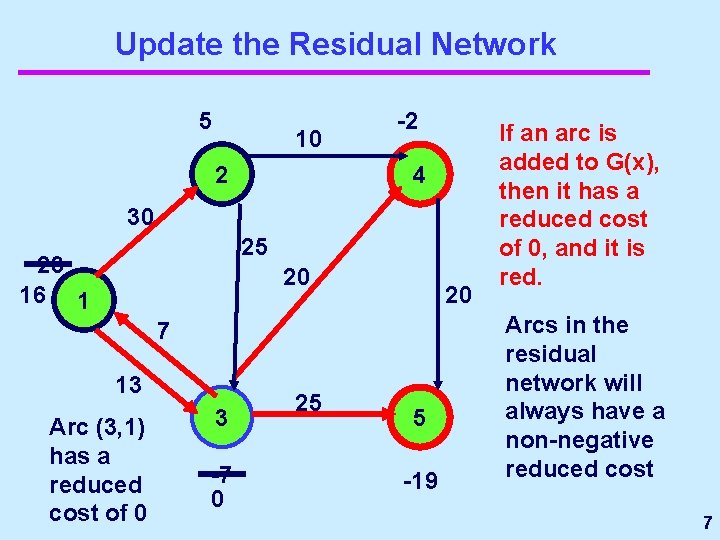
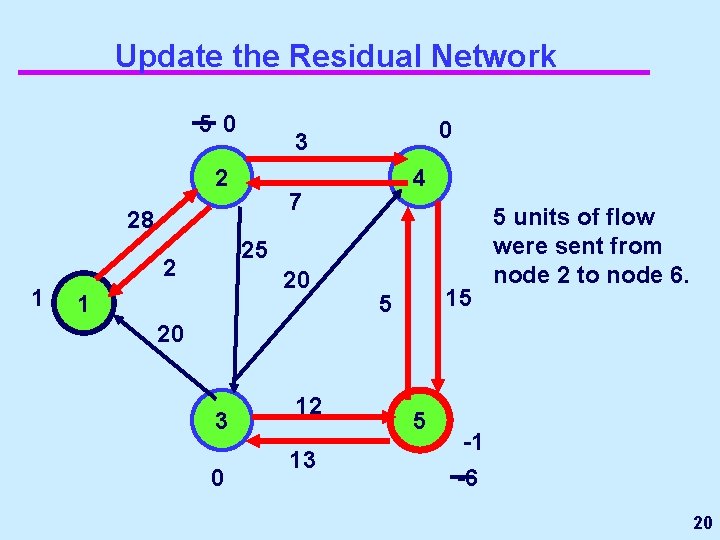
Update the Residual Network 5 10 2 -2 4 30 25 23 16 1 20 20 7 13 Arc (3, 1) has a reduced cost of 0 3 -7 0 25 5 -19 If an arc is added to G(x), then it has a reduced cost of 0, and it is red. Arcs in the residual network will always have a non-negative reduced cost 7

A comment At this point, one would choose a source node, and then find the shortest path from the source node to all other nodes, and then update the residual network. However, there are still paths of 0 reduced cost in the residual network, and it makes sense to use them. This heuristic is quite useful in practice. 8

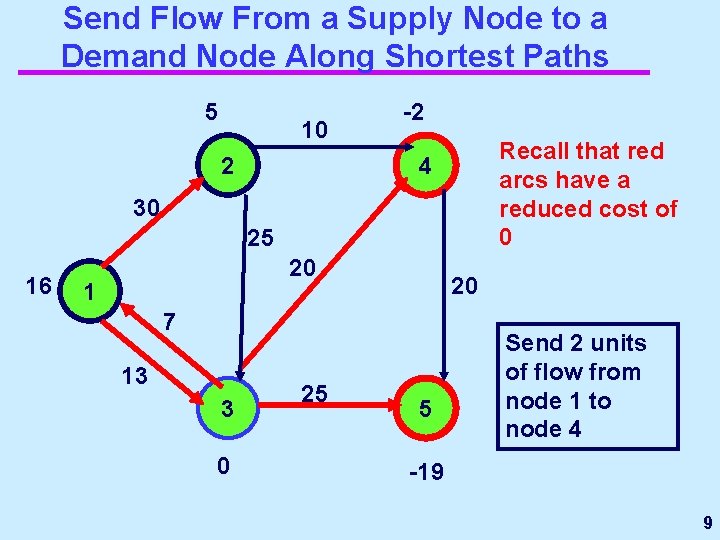
Send Flow From a Supply Node to a Demand Node Along Shortest Paths 5 10 2 -2 Recall that red arcs have a reduced cost of 0 4 30 25 16 20 1 20 7 13 3 0 25 5 Send 2 units of flow from node 1 to node 4 -19 9

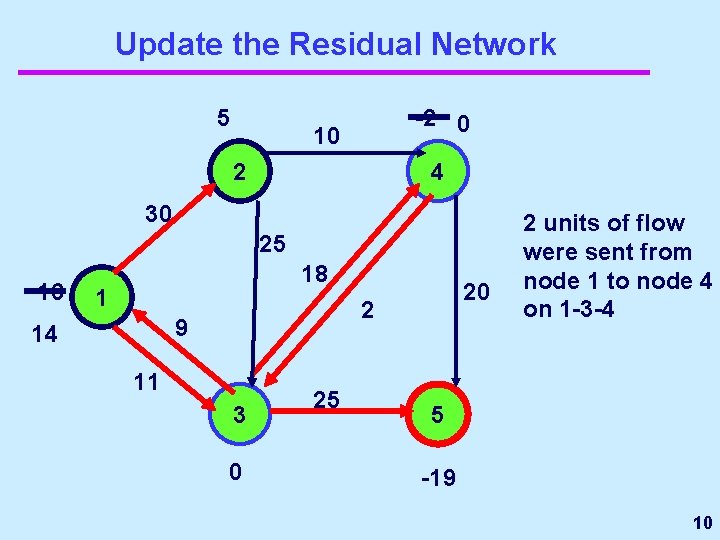
Update the Residual Network 5 -2 0 10 2 4 30 25 16 18 1 2 9 14 20 11 3 0 25 2 units of flow were sent from node 1 to node 4 on 1 -3 -4 5 -19 10

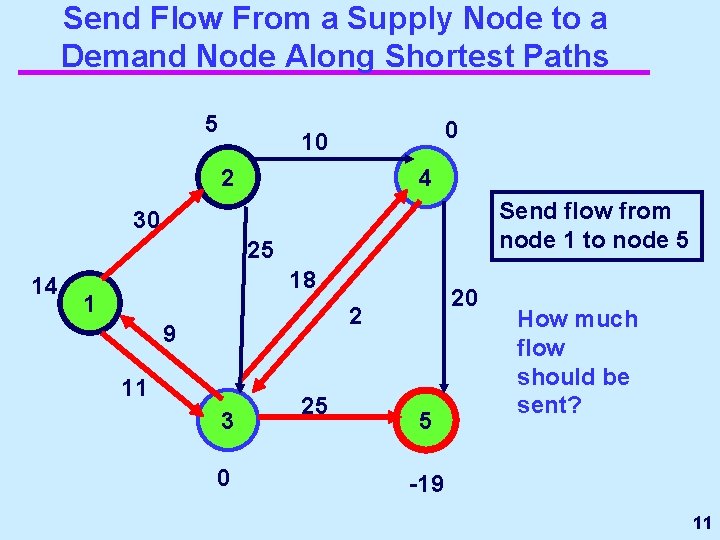
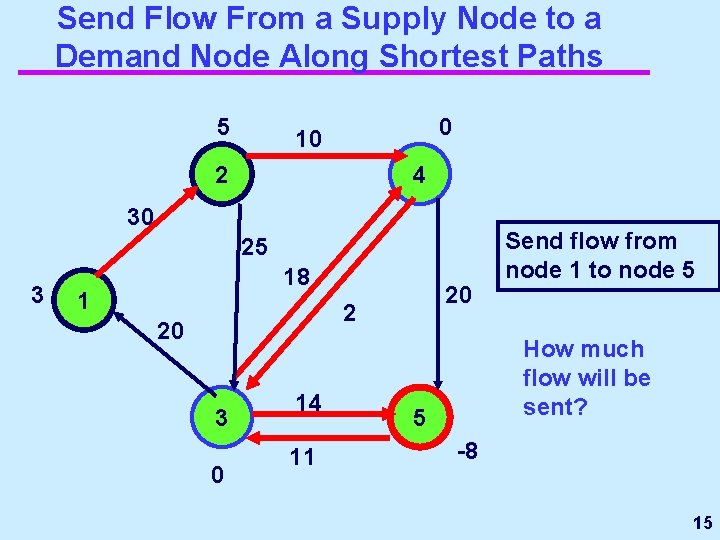
Send Flow From a Supply Node to a Demand Node Along Shortest Paths 5 0 10 2 4 Send flow from node 1 to node 5 30 25 14 18 1 20 2 9 11 3 0 25 5 How much flow should be sent? -19 11

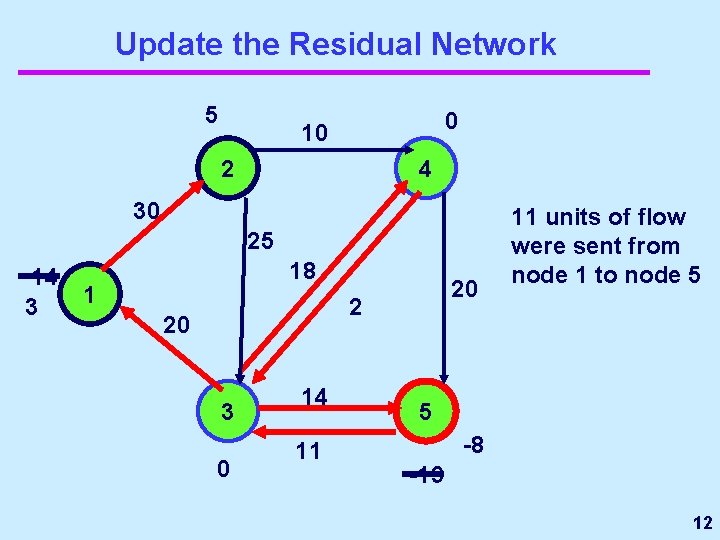
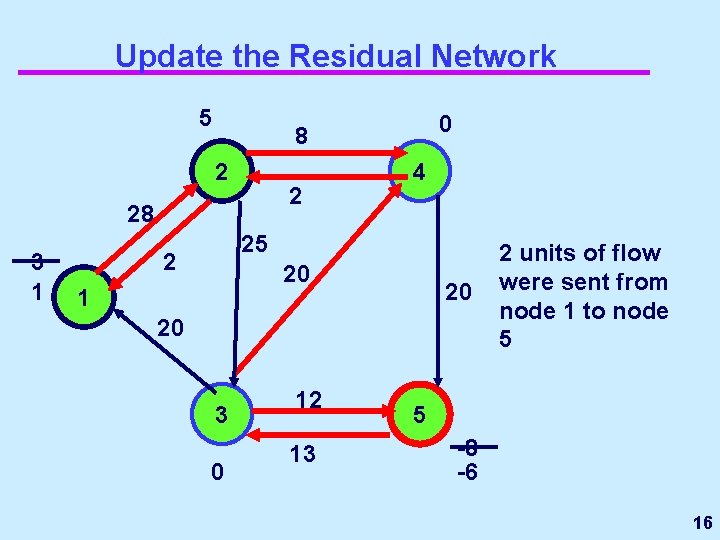
Update the Residual Network 5 0 10 2 4 30 25 14 3 18 1 20 2 20 3 0 14 11 11 units of flow were sent from node 1 to node 5 5 -8 -19 12

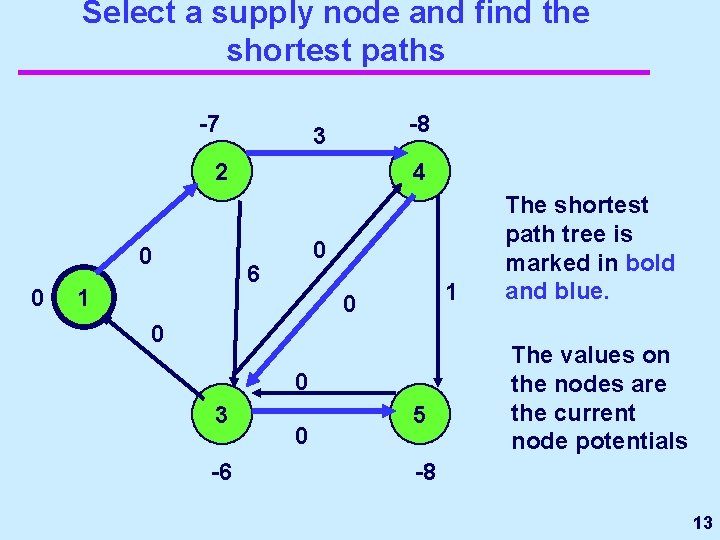
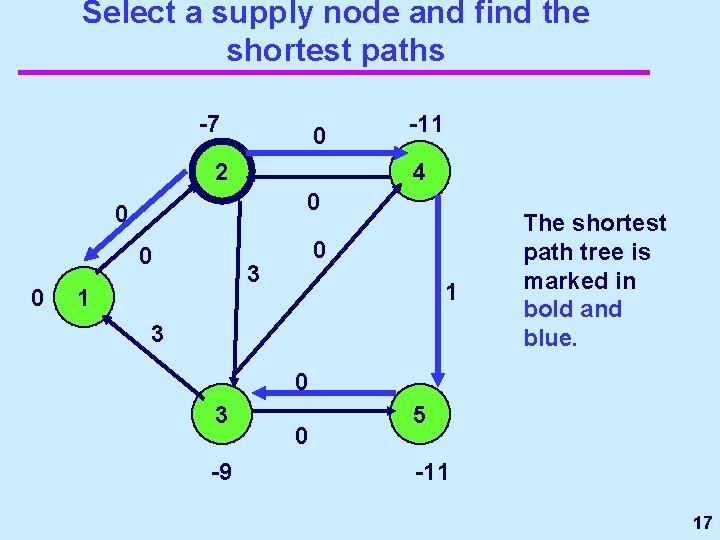
Select a supply node and find the shortest paths -7 -8 3 2 0 0 4 0 6 1 1 0 0 0 3 -6 0 5 The shortest path tree is marked in bold and blue. The values on the nodes are the current node potentials -8 13

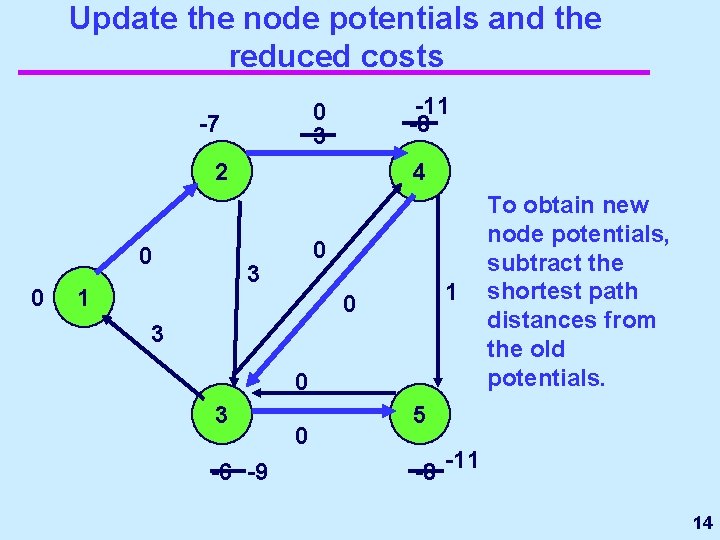
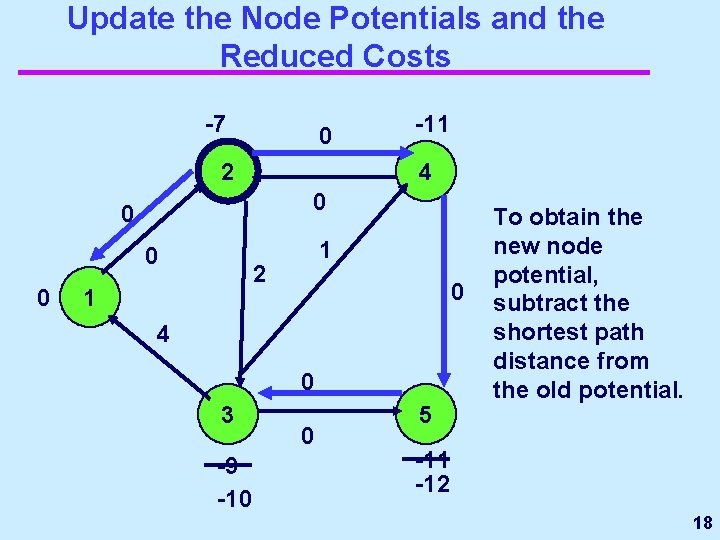
Update the node potentials and the reduced costs -11 -8 0 3 -7 2 0 0 4 0 3 1 1 0 3 -6 -9 0 To obtain new node potentials, subtract the shortest path distances from the old potentials. 5 -8 -11 14

Send Flow From a Supply Node to a Demand Node Along Shortest Paths 5 0 10 2 4 30 25 3 18 1 20 2 20 3 0 14 11 Send flow from node 1 to node 5 How much flow will be sent? 5 -8 15

Update the Residual Network 5 2 2 28 3 1 0 8 4 25 2 20 1 20 20 3 0 12 13 2 units of flow were sent from node 1 to node 5 5 -8 -6 16

Select a supply node and find the shortest paths -7 0 2 4 0 0 -11 0 3 1 1 3 The shortest path tree is marked in bold and blue. 0 3 -9 0 5 -11 17

Update the Node Potentials and the Reduced Costs -7 0 2 4 0 0 -11 1 2 1 0 4 0 3 -9 -10 0 5 To obtain the new node potential, subtract the shortest path distance from the old potential. -11 -12 18

Send Flow From a Supply Node to a Demand Node Along Shortest Paths 5 2 2 28 4 Send flow from node 2 to node 5 25 2 1 0 8 20 1 20 How much flow can be sent? 20 3 0 12 13 5 -6 19

Update the Residual Network 5 0 2 4 7 28 25 2 1 0 3 20 1 15 5 5 units of flow were sent from node 2 to node 6. 20 3 0 12 13 5 -1 -6 20

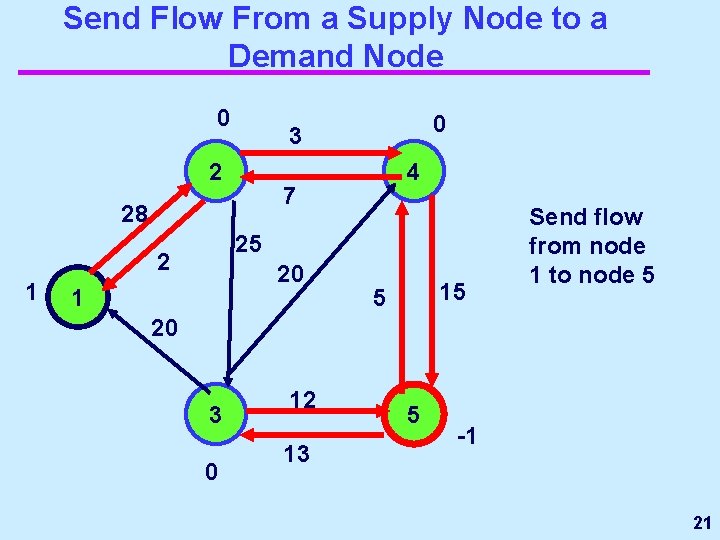
Send Flow From a Supply Node to a Demand Node 0 2 4 7 28 25 2 1 0 3 20 1 15 5 Send flow from node 1 to node 5 20 3 0 12 13 5 -1 21

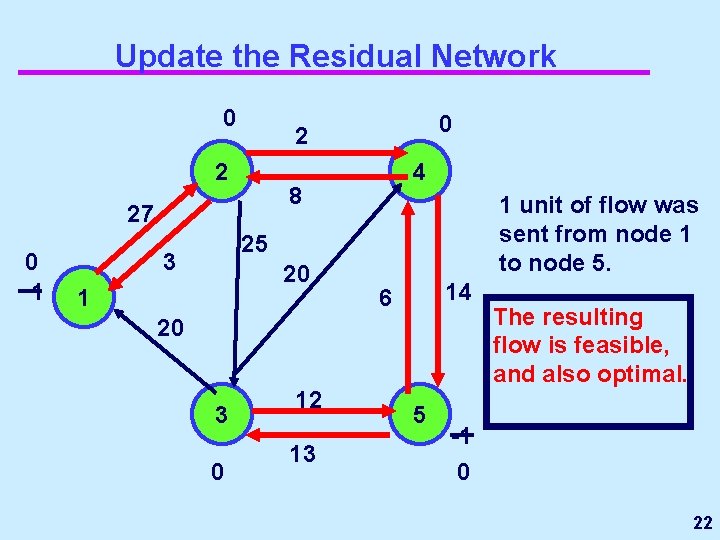
Update the Residual Network 0 2 4 8 27 0 1 0 2 1 unit of flow was sent from node 1 to node 5. 25 3 20 1 14 6 20 3 0 12 13 5 The resulting flow is feasible, and also optimal. -1 0 22

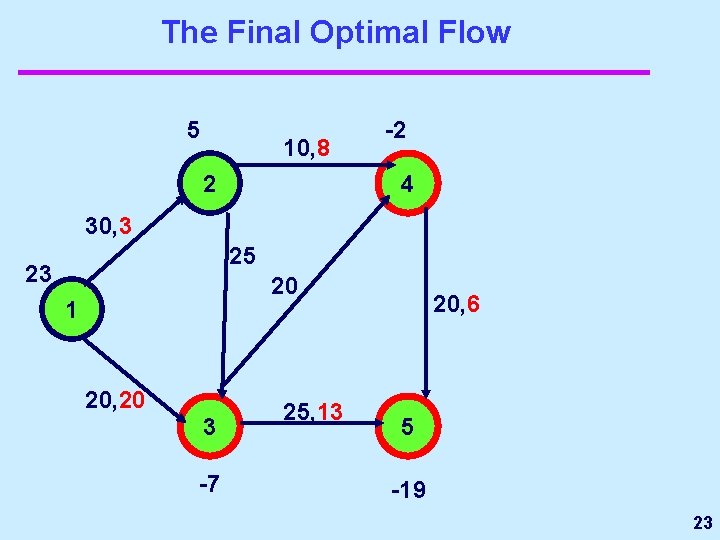
The Final Optimal Flow 5 10, 8 2 -2 4 30, 3 25 23 20 1 20, 20 3 -7 25, 13 20, 6 5 -19 23

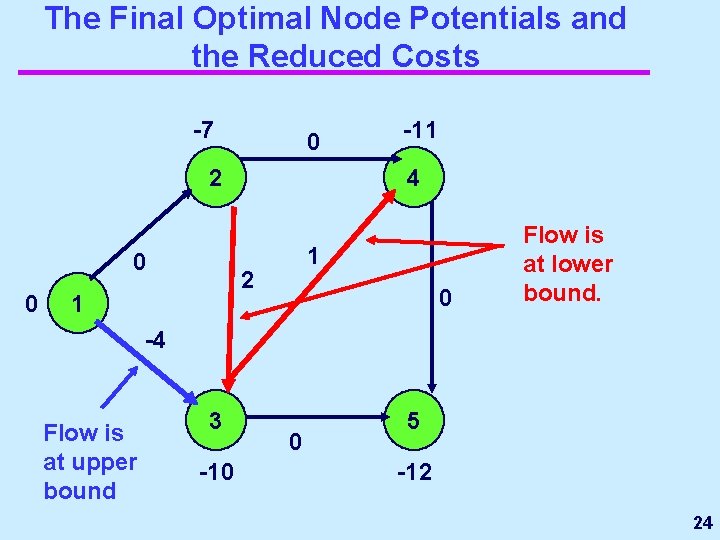
The Final Optimal Node Potentials and the Reduced Costs -7 0 2 0 0 4 1 2 1 -11 0 Flow is at lower bound. -4 Flow is at upper bound 3 -10 0 5 -12 24