14 Memory testing 1 Motivation for testing memories

14. Memory testing 1. Motivation for testing memories (4) 2. Modeling memory chips (6) 3. Reduced functional fault models (17) 4. Traditional tests (7) 5. March tests (7) 6. Pseudorandom memory tests (10)

1. 1 Importance of memories Memories dominate chip area (94% of chip area in 2014) 1. Memories are most defect sensitive parts • Because they are fabricated with minimal feature widths 2. Memories have a large impact on total chip DPM level • Therefore high quality tests required % of chip area 3. (Self) Repair becoming standard for larger memories (> 1 Mbit) year

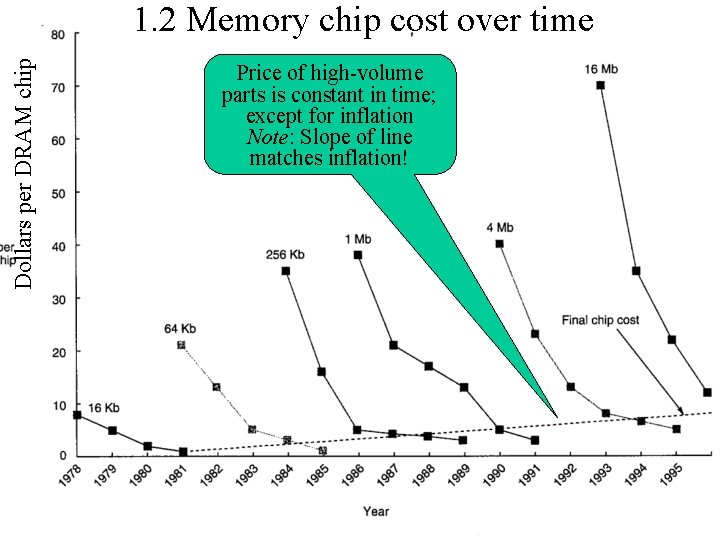
Dollars per DRAM chip 1. 2 Memory chip cost over time Price of high-volume parts is constant in time; except for inflation Note: Slope of line matches inflation!

1. 3 Table with test times • Note: A memory is tested with several algorithms, which together may go through the total address space over 100 times Effective test time for 16 Mb DRAM, using O(n) tests, is about 168 s • Test time reduced using on-chip parallelism (DFT and BIST)

1. 4 Problems with testing memories • Number of bits/chip increases exponentially (4*in <3 years) • Price/bit decreases exponentially • Test cost has to decrease exponentially as well – Older traditional tests were of O(n 2) – Current tests have to be of O(n) or less • DFT and BIST used to reduce test time to about O(n) • Area/cell decreases exponentially – Line widths decrease (more: opens, resistance) – Line distances decrease (more: shorts, couplings) – Cell leakage increases with reduced threshold voltages • Consequence – More complex fault behavior – More global fault behavior (ground bounce, coupling effects) Result: Number of bits to be tested increases exponentially, fault behavior becomes more complex, while test cost has to be same

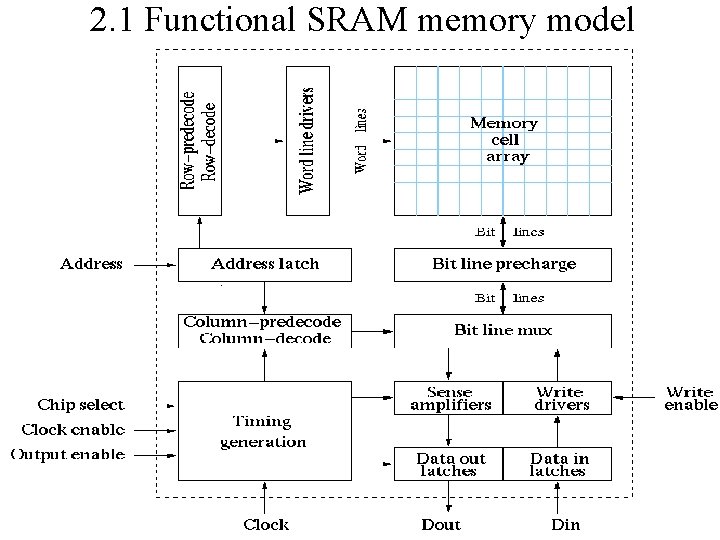
2. 1 Functional SRAM memory model Fig. 4. 2 pag. 35

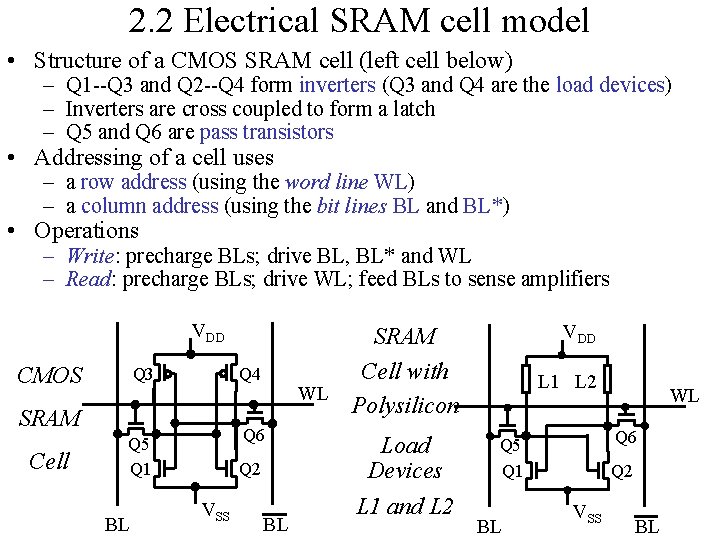
2. 2 Electrical SRAM cell model • Structure of a CMOS SRAM cell (left cell below) – Q 1 --Q 3 and Q 2 --Q 4 form inverters (Q 3 and Q 4 are the load devices) – Inverters are cross coupled to form a latch – Q 5 and Q 6 are pass transistors • Addressing of a cell uses – a row address (using the word line WL) – a column address (using the bit lines BL and BL*) • Operations – Write: precharge BLs; drive BL, BL* and WL – Read: precharge BLs; drive WL; feed BLs to sense amplifiers VDD CMOS Q 3 Q 4 Q 5 Q 1 Q 6 SRAM Cell BL Q 2 VSS VDD SRAM Cell with WL Polysilicon BL Load Devices L 1 and L 2 L 1 L 2 Q 6 Q 5 Q 1 BL WL Q 2 VSS BL

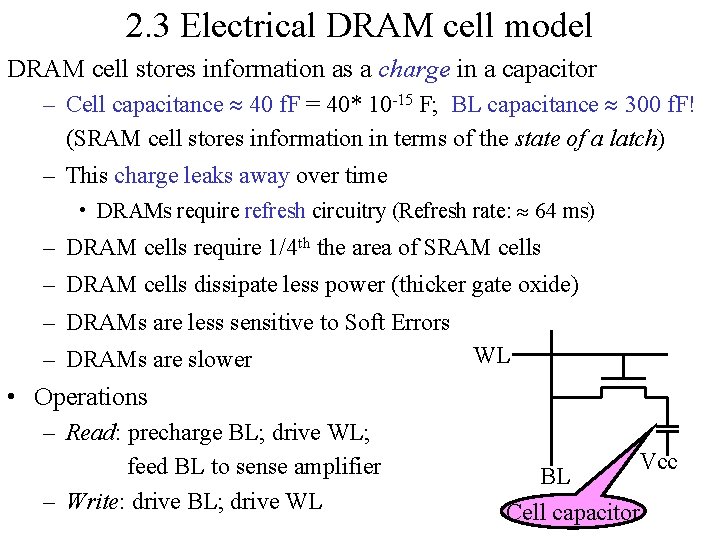
2. 3 Electrical DRAM cell model DRAM cell stores information as a charge in a capacitor – Cell capacitance 40 f. F = 40* 10 -15 F; BL capacitance 300 f. F! (SRAM cell stores information in terms of the state of a latch) – This charge leaks away over time • DRAMs require refresh circuitry (Refresh rate: 64 ms) – DRAM cells require 1/4 th the area of SRAM cells – DRAM cells dissipate less power (thicker gate oxide) – DRAMs are less sensitive to Soft Errors – DRAMs are slower WL • Operations – Read: precharge BL; drive WL; feed BL to sense amplifier – Write: drive BL; drive WL BL Vcc Cell capacitor

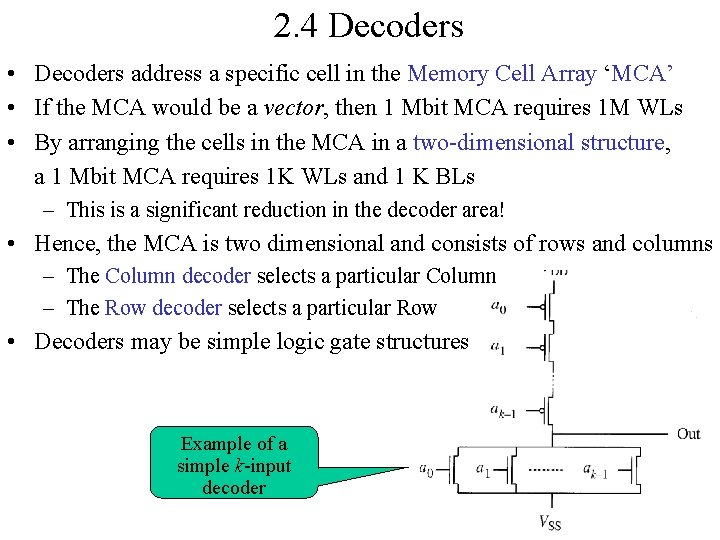
2. 4 Decoders • Decoders address a specific cell in the Memory Cell Array ‘MCA’ • If the MCA would be a vector, then 1 Mbit MCA requires 1 M WLs • By arranging the cells in the MCA in a two-dimensional structure, a 1 Mbit MCA requires 1 K WLs and 1 K BLs – This is a significant reduction in the decoder area! • Hence, the MCA is two dimensional and consists of rows and columns – The Column decoder selects a particular Column – The Row decoder selects a particular Row • Decoders may be simple logic gate structures Example of a simple k-input decoder

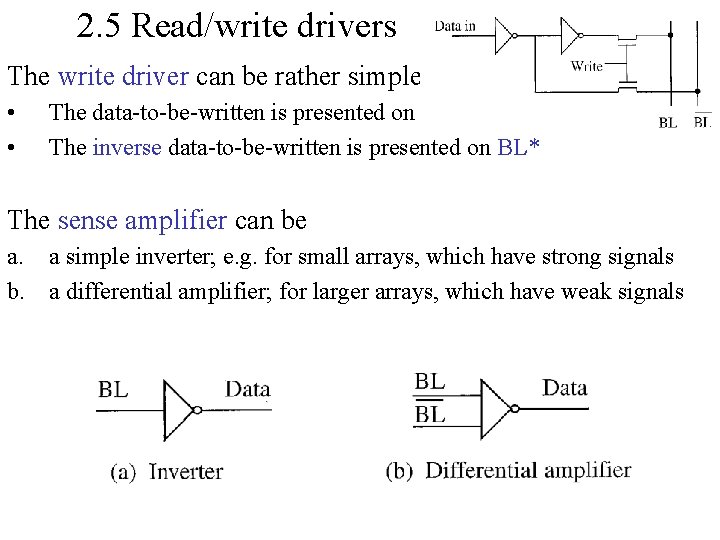
2. 5 Read/write drivers The write driver can be rather simple • • The data-to-be-written is presented on BL The inverse data-to-be-written is presented on BL* The sense amplifier can be a. a simple inverter; e. g. for small arrays, which have strong signals b. a differential amplifier; for larger arrays, which have weak signals

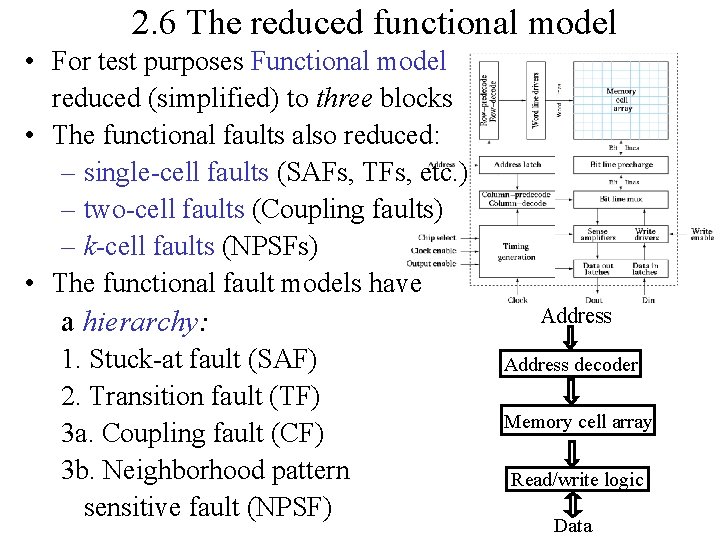
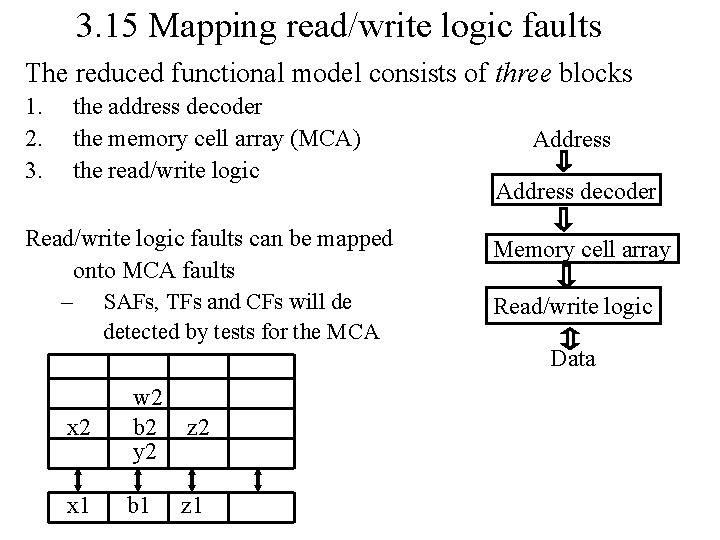
2. 6 The reduced functional model • For test purposes Functional model reduced (simplified) to three blocks • The functional faults also reduced: – single-cell faults (SAFs, TFs, etc. ) – two-cell faults (Coupling faults) – k-cell faults (NPSFs) • The functional fault models have a hierarchy: 1. Stuck-at fault (SAF) 2. Transition fault (TF) 3 a. Coupling fault (CF) 3 b. Neighborhood pattern sensitive fault (NPSF) Address decoder Memory cell array Read/write logic Data

3. 1 Notation for describing faults • <…> describes a fault • <S/F> describes a single-cell fault – S describes the state/operation sensitizing the fault • A fault is sensitized when the fault effect is made present – F describes the fault effect in the victim cell (v-cell) • <S; F> describes a two-cell fault (a Coupling Fault) – S describes the state/operation of the aggressor cell (a-cell) sensitizing the fault – F describes the fault effect in the v-cell 1 -cell fault • Examples <S/F> – < /0>: a SA 0 fault < /1>: a SA 1 fault – < /0>: an TF < /1>: a TF – < ; 0>: a CFid < ; 1>: a CFid / 2 -cell fault <S; F> ;

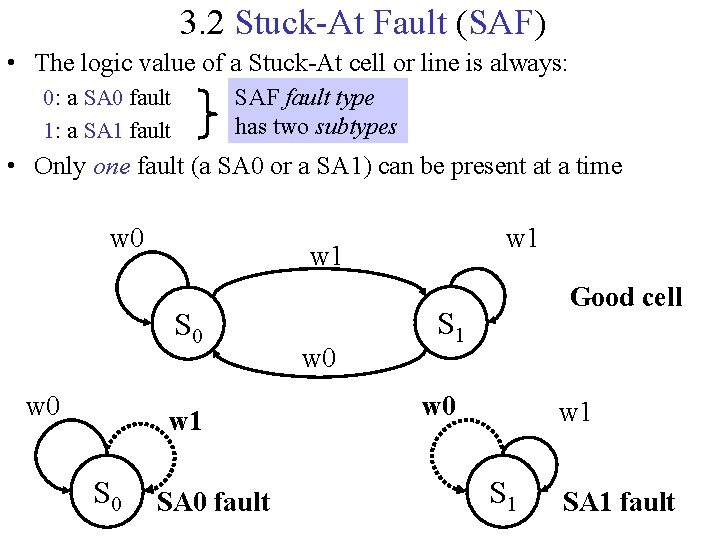
3. 2 Stuck-At Fault (SAF) • The logic value of a Stuck-At cell or line is always: SAF fault type has two subtypes 0: a SA 0 fault 1: a SA 1 fault • Only one fault (a SA 0 or a SA 1) can be present at a time w 0 w 1 SA 0 fault w 0 Good cell S 1 w 0 w 1 SA 1 fault

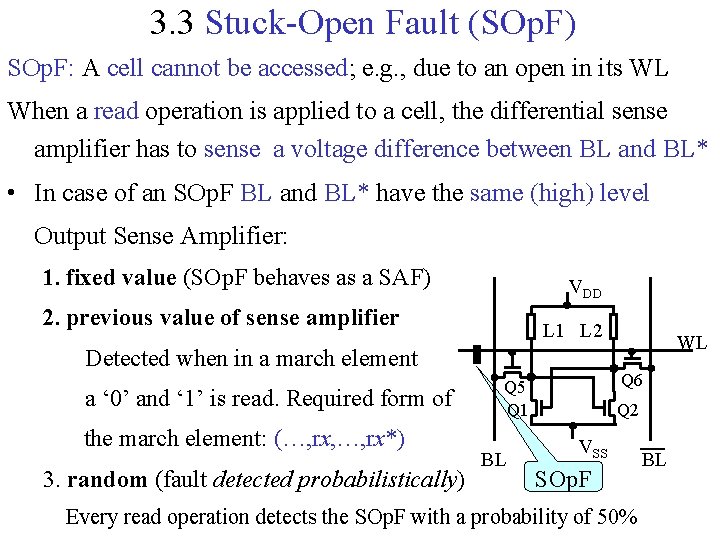
3. 3 Stuck-Open Fault (SOp. F) SOp. F: A cell cannot be accessed; e. g. , due to an open in its WL When a read operation is applied to a cell, the differential sense amplifier has to sense a voltage difference between BL and BL* • In case of an SOp. F BL and BL* have the same (high) level Output Sense Amplifier: 1. fixed value (SOp. F behaves as a SAF) VDD 2. previous value of sense amplifier L 1 L 2 Detected when in a march element a ‘ 0’ and ‘ 1’ is read. Required form of the march element: (…, rx, …, rx*) 3. random (fault detected probabilistically) Q 6 Q 5 Q 1 BL WL Q 2 VSS SOp. F Every read operation detects the SOp. F with a probability of 50% BL

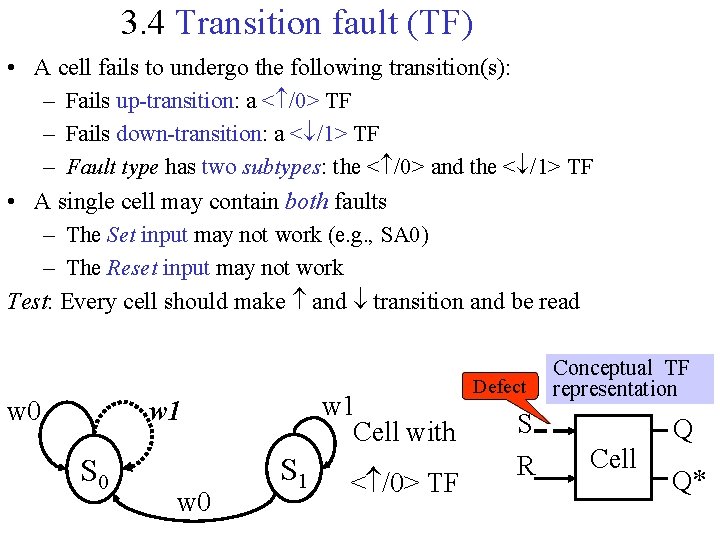
3. 4 Transition fault (TF) • A cell fails to undergo the following transition(s): – Fails up-transition: a < /0> TF – Fails down-transition: a < /1> TF – Fault type has two subtypes: the < /0> and the < /1> TF • A single cell may contain both faults – The Set input may not work (e. g. , SA 0) – The Reset input may not work Test: Every cell should make and transition and be read w 0 w 1 Cell with w 1 S 0 w 0 S 1 < /0> TF Defect Conceptual TF representation S R Cell Q Q*

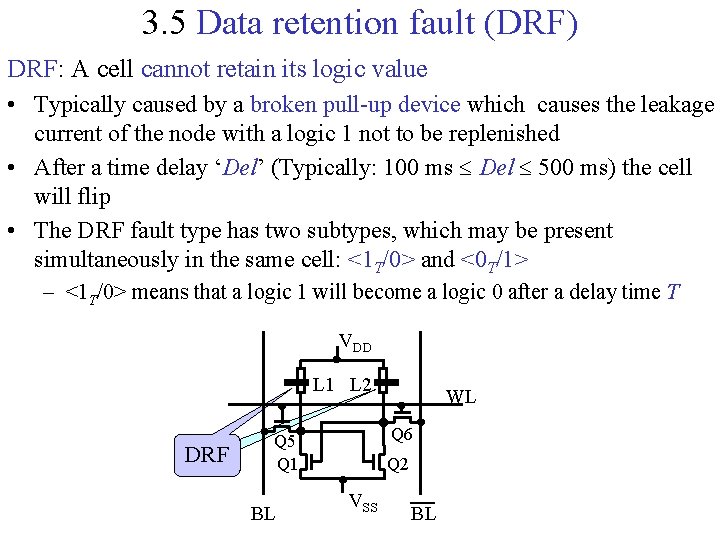
3. 5 Data retention fault (DRF) DRF: A cell cannot retain its logic value • Typically caused by a broken pull-up device which causes the leakage current of the node with a logic 1 not to be replenished • After a time delay ‘Del’ (Typically: 100 ms Del 500 ms) the cell will flip • The DRF fault type has two subtypes, which may be present simultaneously in the same cell: <1 T/0> and <0 T/1> – <1 T/0> means that a logic 1 will become a logic 0 after a delay time T VDD L 1 L 2 DRF Q 6 Q 5 Q 1 BL WL Q 2 VSS BL

3. 6 Faults involving 2 cells: Coupling Faults ‘CFs’ CF: The state of, or an operation applied to, the a-cell (aggressor cell) forces or changes the state of the v-cell (victim cell) • Fault type Idempotent CF: CFid – A transition write operation ( =0 1 & =1 0 change) applied to the a-cell forces the contents of the v-cell – CFid has 4 subtypes: < ; 0>, < ; 1>, < ; 0> and < ; 1> • The or write operations to a-cell sensitize the fault • The ‘ 0’ or ‘ 1’ are the fault effect in the v-cell – In addition, each subtype has two positions: A. address of a-cell < address of v-cell B. address of a-cell > address of v-cell a-cell < ; 0> A v-cell < ; 0> B a-cell

3. 7 Coupling faults (CFst, CFin) • State CF (CFst): A CF whereby the state of the a-cell forces a fixed value in the v-cell – Four fault subtypes : <1; 0>, <1; 1>, <0; 0> and <0; 1> – Each subtype has 2 positions: • addr. a-cell < addr. v-cell • addr. a-cell > addr. v-cell • Inversion CF (CFin): A transition write operation to the a-cell toggles the contents of the v-cell (Note: denotes toggling) – Two fault subtypes exist: < ; > and < ; > – Each subtype has 2 positions: • addr. a-cell > addr. v-cell • addr. a-cell < addr. v-cell Note: CFin not a realistic fault An SRAM cell is a latch, rather then a flip-flop Cannot toggle!

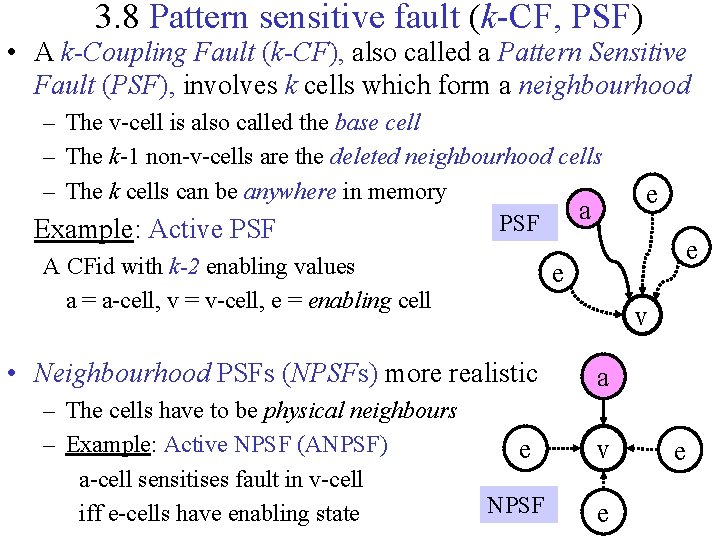
3. 8 Pattern sensitive fault (k-CF, PSF) • A k-Coupling Fault (k-CF), also called a Pattern Sensitive Fault (PSF), involves k cells which form a neighbourhood – The v-cell is also called the base cell – The k-1 non-v-cells are the deleted neighbourhood cells – The k cells can be anywhere in memory a PSF Example: Active PSF A CFid with k-2 enabling values a = a-cell, v = v-cell, e = enabling cell e e v • Neighbourhood PSFs (NPSFs) more realistic – The cells have to be physical neighbours – Example: Active NPSF (ANPSF) a-cell sensitises fault in v-cell iff e-cells have enabling state e e NPSF a v e e

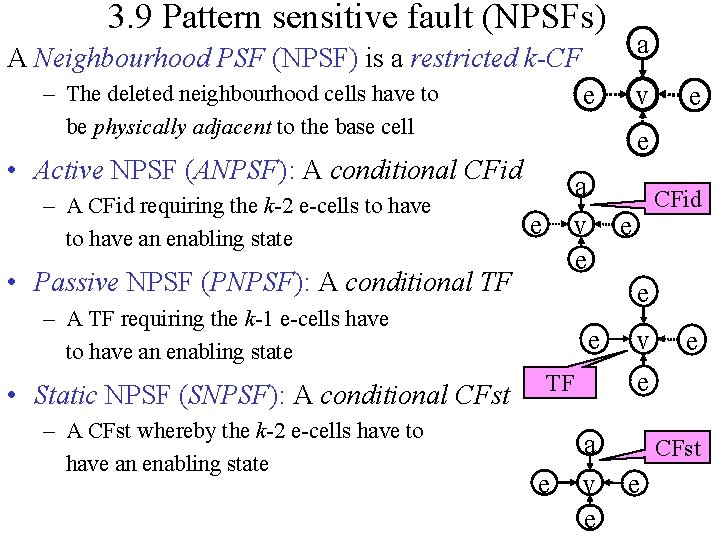
3. 9 Pattern sensitive fault (NPSFs) a A Neighbourhood PSF (NPSF) is a restricted k-CF e – The deleted neighbourhood cells have to be physically adjacent to the base cell a v e e • Passive NPSF (PNPSF): A conditional TF – A CFst whereby the k-2 e-cells have to have an enabling state CFid e e – A TF requiring the k-1 e-cells have to have an enabling state • Static NPSF (SNPSF): A conditional CFst e e • Active NPSF (ANPSF): A conditional CFid – A CFid requiring the k-2 e-cells to have an enabling state v e TF e a v e e CFst e

Performed by (Dekker, ITC’ 88) for SRAMs • 8 K*8 = 64 Kbits, 4 Transistor (4 T) cells • technology: 4 m (Note: R-defect is defect resistivity) • Distribution for R-defect values assumed to be uniform – i. e. , no FAB statistics taken into account Probability 3. 10 Validation of the fault models R-defect Table shows likelihood of functional faults, as a function of the spot defect size Results: Two new fault models established: SOp. F and DRF SAFs 50% CFs due to large spot defects CFin not present!

3. 11 March tests: Concept and notation • A march test consists of a sequence of march elements • A march element consists of a sequence of operations applied to every cell, in either one of two address orders: 1. Increasing ( ) address order; from cell 0 to cell n-1 2. Decreasing ( ) address order; from cell n-1 to cell 0 Note: The address order may be any sequence of addresses (e. g. , 5, 2, 0, 1, 3, 4, 6, 7), provided that the address order is the exact reverse sequence (i. e, 7, 6, 4, 3, 1, 0, 2, 5) • Example: MATS+ { (w 0); (r 0, w 1); (r 1, w 0)} – Test consists of 3 march elements: M 0, M 1 and M 2 – The address order of M 0 is irrelevant (Denoted by symbol ) M 0: (w 0) means ‘for i = 0 to n-1 do A[i]: =0’ M 1: (r 0, w 1) means ‘for i = 0 to n-1 do {read A[i]; A[i]: =1}’ M 2: (r 1, w 0) means ‘for i = n-1 to 0 do {read A[i]; A[i]: =0}’

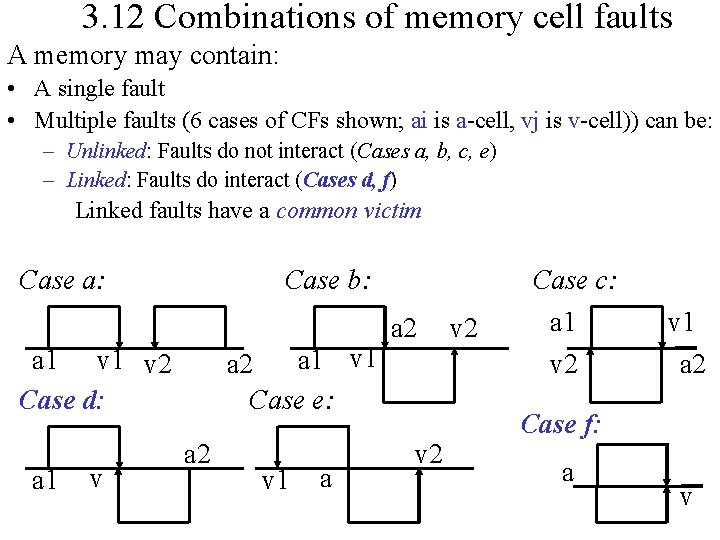
3. 12 Combinations of memory cell faults A memory may contain: • A single fault • Multiple faults (6 cases of CFs shown; ai is a-cell, vj is v-cell)) can be: – Unlinked: Faults do not interact (Cases a, b, c, e) – Linked: Faults do interact (Cases d, f) Linked faults have a common victim Case a: Case b: a 1 v 1 a 2 Case e: a 1 v 2 Case d: a 1 v a 2 v 1 a a 2 v 2 Case c: a 1 v 2 v 1 a 2 Case f: a v

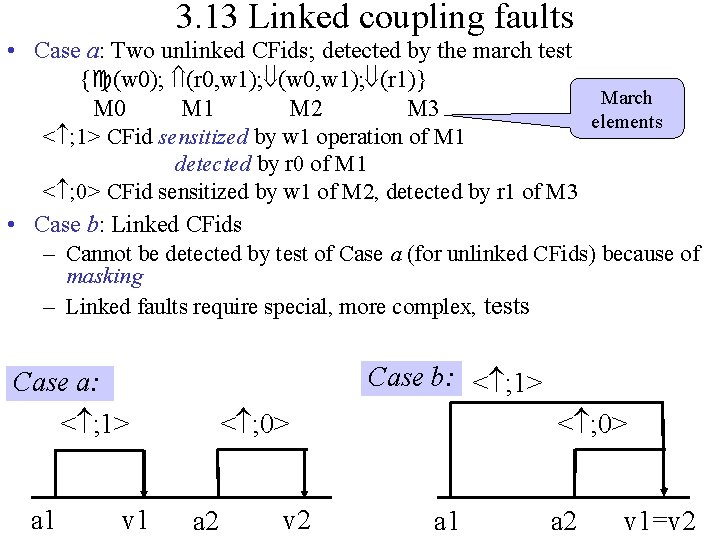
3. 13 Linked coupling faults • Case a: Two unlinked CFids; detected by the march test { (w 0); (r 0, w 1); (w 0, w 1); (r 1)} March M 0 M 1 M 2 M 3 elements < ; 1> CFid sensitized by w 1 operation of M 1 detected by r 0 of M 1 < ; 0> CFid sensitized by w 1 of M 2, detected by r 1 of M 3 • Case b: Linked CFids – Cannot be detected by test of Case a (for unlinked CFids) because of masking – Linked faults require special, more complex, tests Case b: < ; 1> Case a: < ; 1> a 1 v 1 < ; 0> a 2 v 2 < ; 0> a 1 a 2 v 1=v 2

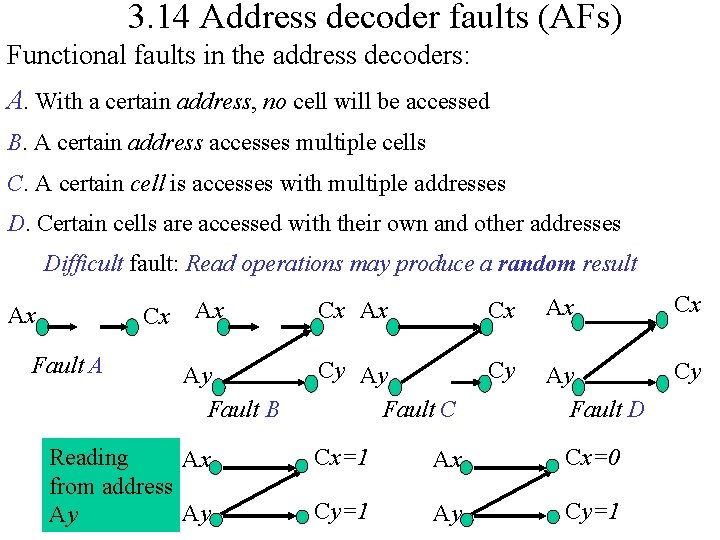
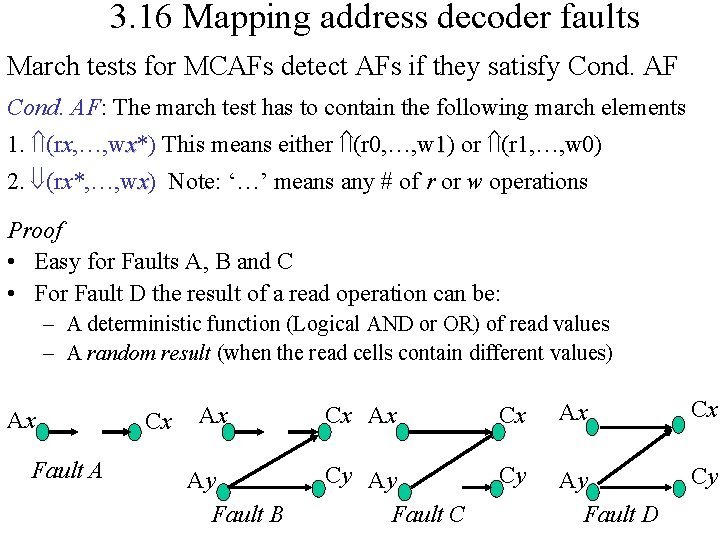
3. 14 Address decoder faults (AFs) Functional faults in the address decoders: A. With a certain address, no cell will be accessed B. A certain address accesses multiple cells C. A certain cell is accesses with multiple addresses D. Certain cells are accessed with their own and other addresses Difficult fault: Read operations may produce a random result Ax Cx Fault A Ax Ay Fault B Reading Ax from address Ay Ay Cx Ax Cx Cy Ay Fault C Cy Ay Fault D Cy Cx=1 Ax Cx=0 Cy=1 Ay Cy=1

3. 15 Mapping read/write logic faults The reduced functional model consists of three blocks 1. 2. 3. the address decoder the memory cell array (MCA) the read/write logic Read/write logic faults can be mapped onto MCA faults – SAFs, TFs and CFs will de detected by tests for the MCA Address decoder Memory cell array Read/write logic Data x 2 w 2 b 2 y 2 z 2 x 1 b 1 z 1

3. 16 Mapping address decoder faults March tests for MCAFs detect AFs if they satisfy Cond. AF: The march test has to contain the following march elements 1. (rx, …, wx*) This means either (r 0, …, w 1) or (r 1, …, w 0) 2. (rx*, …, wx) Note: ‘…’ means any # of r or w operations Proof • Easy for Faults A, B and C • For Fault D the result of a read operation can be: – A deterministic function (Logical AND or OR) of read values – A random result (when the read cells contain different values) Ax Fault A Cx Ax Ay Fault B Cx Ax Cx Cy Ay Fault C Cy Ay Fault D Cy

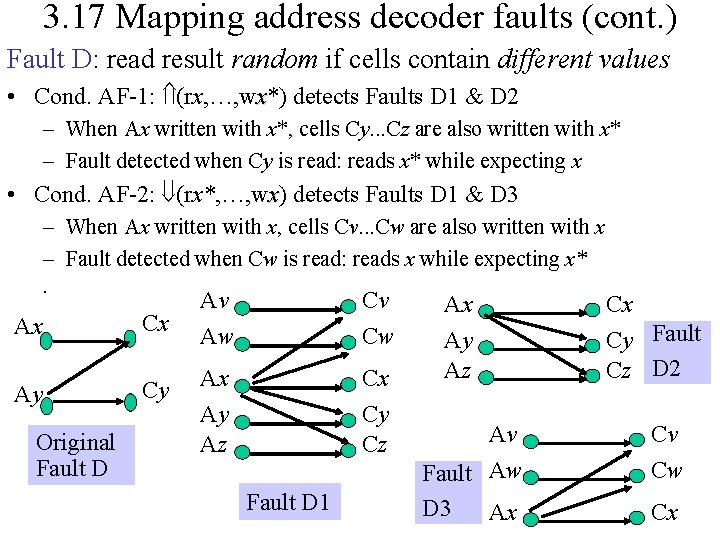
3. 17 Mapping address decoder faults (cont. ) Fault D: read result random if cells contain different values • Cond. AF-1: (rx, …, wx*) detects Faults D 1 & D 2 – When Ax written with x*, cells Cy. . . Cz are also written with x* – Fault detected when Cy is read: reads x* while expecting x • Cond. AF-2: (rx*, …, wx) detects Faults D 1 & D 3 – When Ax written with x, cells Cv. . . Cw are also written with x – Fault detected when Cw is read: reads x while expecting x*. Ax Cx Ay Cy Original Fault D Av Aw Cv Cw Ax Ay Az Cx Cy Cz Fault D 1 Ax Ay Az Av Fault Aw D 3 Ax Cx Cy Fault Cz D 2 Cv Cw Cx

4. 1 Functional RAM chip testing • Purpose 1. Cover traditional tests (5) • Zero-One (MSCAN) • Checkerboard • GALPAT and Walking 1/0 2. Cover tests for stuck-at, transition and coupling faults (6) • MATS and MATS+ • March C • March A and March B 3. Comparison of march tests (1)

4. 2 Fault coverage of tests • When a test detects faults of a particular fault type, it detects: – all subtypes of that type; e. g. , if it detects TFs is has to detect all < /0> and < /1> TFs – all positions of each subtype (addr. a-cell < or > v-cell) • A complete test detects all faults it is designed for It may, additionally, and unintentionally, detect also other faults But not all subtypes and not all positions of each of these faults Example: MATS+ : { (w 0); (r 0, w 1); (r 1, w 0)} • Detects all AFs • Detects all SAFs • Detects all < /0> TFs • Does not detect all < /1> TFs MATS+ does not detect TFs Fault coverage of MATS+ < /0> TFs AFs, SAFs

4. 3 Traditional tests • Traditional tests are older tests – Usually developed without explicitly using fault models – Usually they also have a relatively long test time – Some have special properties in terms of: • detecting dynamic faults • locating (rather than only detecting) faults • Many traditional tests exist: 1. Zero-One (Usually referred to as Scan Test or MSCAN) 2. Checkerboard 3. GALPAT and Walking 1/0 4. Sliding Diagonal 5. Butterfly 6. Many, many others

4. 4 Zero-One test (Scan test, (M)SCAN) • Minimal test, consisting of writing & reading 0 s and 1 s – – Step 1: write 0 in all cells Step 2: read all cells Step 3: write 1 in all cells Step 4: read all cells • March notation for Scan test: { (w 0); (r 0); (w 1); (r 1)} • Test length: 4*n operations; which is O(n) • Fault detection capability: AFs not detected – Condition AF not satisfied: 1. (rx, …, wx*) 2. (rx*, …, wx) – If address decoder maps all addresses to a single cell, then it can only be guaranteed that one cell is fault free – Special property: Stresses read/write & precharge circuits when Fast X addressing is used and sequence of write/read 0101. . data in a column! Fast X addressing Rows Columns Row stripe 000000 111111 Checker 010101 board 1010101 101010

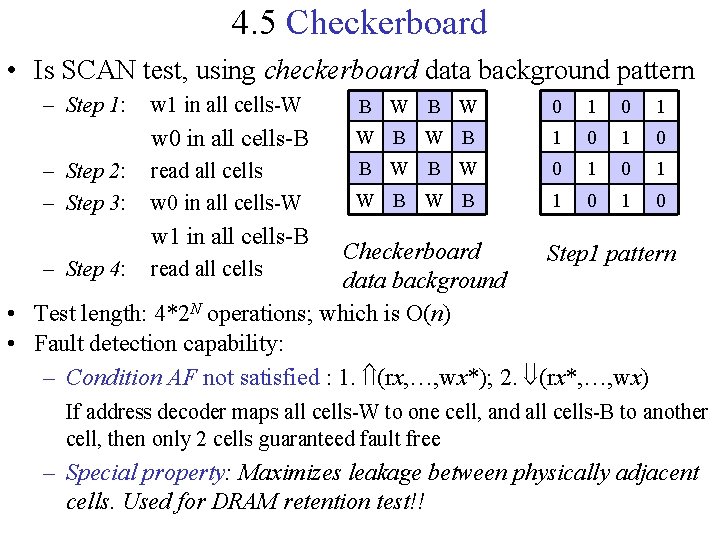
4. 5 Checkerboard • Is SCAN test, using checkerboard data background pattern – Step 1: – Step 2: – Step 3: w 1 in all cells-W B W 0 1 w 0 in all cells-B W B 1 0 read all cells w 0 in all cells-W B W 0 1 W B 1 0 w 1 in all cells-B Checkerboard Step 1 pattern – Step 4: read all cells data background • Test length: 4*2 N operations; which is O(n) • Fault detection capability: – Condition AF not satisfied : 1. (rx, …, wx*); 2. (rx*, …, wx) If address decoder maps all cells-W to one cell, and all cells-B to another cell, then only 2 cells guaranteed fault free – Special property: Maximizes leakage between physically adjacent cells. Used for DRAM retention test!!

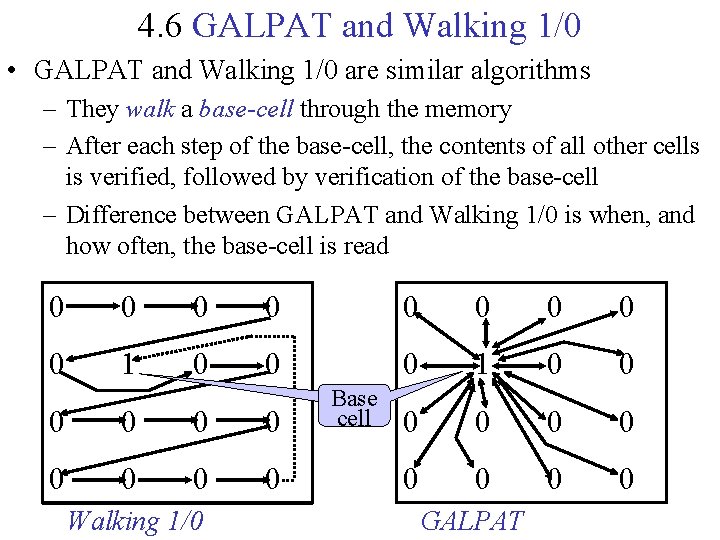
4. 6 GALPAT and Walking 1/0 • GALPAT and Walking 1/0 are similar algorithms – They walk a base-cell through the memory – After each step of the base-cell, the contents of all other cells is verified, followed by verification of the base-cell – Difference between GALPAT and Walking 1/0 is when, and how often, the base-cell is read 0 0 0 0 0 1 0 0 0 0 0 Walking 1/0 Base cell GALPAT

4. 7 GALPAT and Walking 1/0: Properties • • Tests can locate faults GALPAT detects write recovery faults (Cause: slow addr. decoders) Test length: O(n 2): Not acceptable for practical purposes Most coupling faults in a memory are due to sharing – a WL and the column decoder: cells in the same row – BLs and row decoder: cells in the same column • Subsets of GALPAT and Walking I/O used (BC= Base-Cell) – GALROW and Walk. ROW: Read Action on cells in row of BC GALROW 0 1 0 0 – GALCOL and Walk. COL: Read Action on cells in column of BC Test length (assuming n 1/2 rows and n 1/2 columns): O(n 3/2) Note: Test time for 4 Mb 150 ns memory – For O(n 2) test = O(20 days), and for O(n 3/2 ) test = O(14 sec. )

5. 1 March tests The simplest, and most efficient tests for detecting AFs, SAFs, TFs and CFs are march tests The following march tests are covered: – MATS+ • Detects AFs and SAFs – March C • Detects AFs, SAFs, TFs, and unlinked CFins, CFsts, CFids – March A • Detects AFs, SAFs, TFs, CFins, CFsts, CFids, linked CFids (but not linked with TFs) – March B • Detects AFs, SAFs, TFs, CFins, CFsts, CFids, linked CFids

5. 2 MATS+ • MATS+ algorithm: { (w 0); (r 0, w 1); (r 1, w 0)} • Fault coverage – AFs detected because MATS+ satisfies Cond. AF (When reads, accessing multiple cells, return a random value) Cond. AF: 1. (rx, …, wx*) and 2. (rx*, …, wx) (1) satisfied by: (r 0, w 1) and (2) by: (r 1, w 0) • – SAFs are detected: from each cell the value 0 and 1 is read Test length: 5*n Note: If fault model is symmetric with respect to 0/1, / , and with respect to address a-cell < v-cell and address a-cell > v-cell, then each march tests has 3 equivalent tests 0 s 1 s: { (w 0); (r 0, w 1); (r 1, w 0)} { (w 1); (r 1, w 0); (r 0, w 1)} s s: { (w 0); (r 0, w 1); (r 1, w 0)}

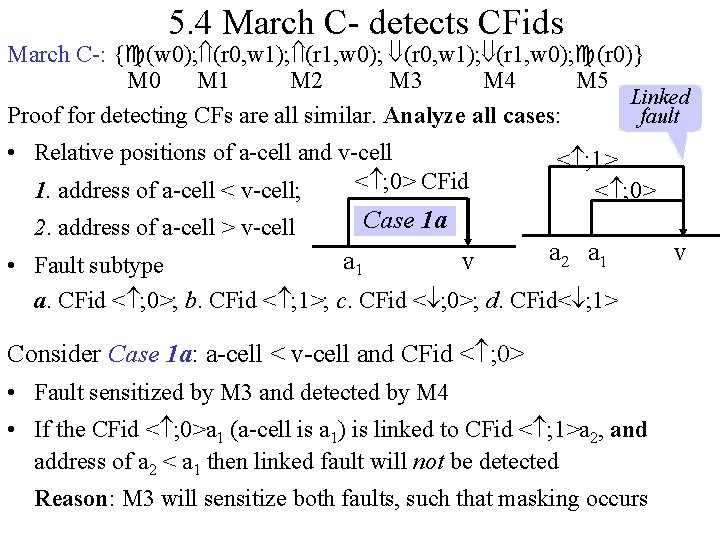
5. 3 March C • March C (Marinescu, 1982): an 11*n algorithm { (w 0); (r 0, w 1); (r 1, w 0); (r 0)} It can be shown that middle ‘ (r 0)’ march element is redundant • March C- (van de Goor, 1991): a 10*n algorithm { (w 0); (r 0, w 1); (r 1, w 0); (r 0)} M 0 M 1 M 2 M 3 M 4 M 5 • Fault coverage of March C– AFs: Cond. AF satisfied by M 1 and M 4, or by M 2 and M 3 – SAFs: Detected by M 1 (SA 1 faults) and M 2 (SA 0 faults) – TFs: < /0> TFs sensitized by M 1, detected by M 2 (and M 3+M 4) < /1> TFs sensitized by M 2, detected by M 3 (and M 4+M 5) – CFins detected – CFsts detected – CFids detected (see proof)

5. 4 March C- detects CFids March C-: { (w 0); (r 0, w 1); (r 1, w 0); (r 0)} M 0 M 1 M 2 M 3 M 4 M 5 Linked fault Proof for detecting CFs are all similar. Analyze all cases: • Relative positions of a-cell and v-cell < ; 0> CFid 1. address of a-cell < v-cell; 2. address of a-cell > v-cell < ; 1> < ; 0> Case 1 a a a 2 1 a 1 v • Fault subtype a. CFid < ; 0>; b. CFid < ; 1>; c. CFid < ; 0>; d. CFid< ; 1> Consider Case 1 a: a-cell < v-cell and CFid < ; 0> • Fault sensitized by M 3 and detected by M 4 • If the CFid < ; 0>a 1 (a-cell is a 1) is linked to CFid < ; 1>a 2, and address of a 2 < a 1 then linked fault will not be detected Reason: M 3 will sensitize both faults, such that masking occurs v

5. 5 March A & March B • March A algorithm (Suk, 1981) { (w 0); (r 0, w 1, w 0, w 1); (r 1, w 0, w 1, w 0); (r 0, w 1, w 0)} M 0 M 1 M 2 M 3 M 4 • March A (Test length: 15*n) detects – AFs, SAFs, TFs, CFins, CFsts, CFids – Linked CFids, but not linked with TFs – March A is complete: detects all intended faults – March A is irredundant: no operation can be removed • March B algorithm (Test length: 17*n) { (w 0); (r 0, w 1, r 1, w 0, r 0, w 1); (r 1, w 0, w 1, w 0); (r 0, w 1, w 0)} M 0 M 1 M 2 M 3 M 4 – Detects all faults of March A – Detects CFids linked with TFs, because M 1 detects all TFs

5. 6 Test requirements for detecting SOp. Fs An SOp. F is caused by an open WL which makes the cell inaccessible • To detect SOp. Fs, assuming a non-transparent sense amplifier, a march test has to verify that a 0 and a 1 has to be read from every cell • This will be the case when the march test contains the March Element ‘ME’ of the form: (…, rx, …, rx*, …), for x = 0 and x = 1. – This ME may be broken down into two MEs of the form: (…, rx, …) & (…, rx*, …), for x = 0 and x = 1. Example: The ME “ (r 0, w 1, r 1, w 0, r 0, w 1)” satisfies the above requirement Note: Any test can be changed to detect SOp. Fs by making sure that the above requirement is satisfied by possibly adding a rx and/or a rx* operation to a ME Example: MATS+ { (w 0); (r 0, w 1); (r 1, w 0)} becomes { (w 0); (r 0, w 1, r 1); (r 1, w 0, r 0)} VDD L 1 L 2 Q 6 Q 5 Q 1 BL WL Q 2 VSS SOp. F BL

5. 7 Test requirements for detecting DRFs Any march test can be extended to detect DRFs • Every cell has to be brought into one state • A time period (Del) has to be waited for the fault to develop – Note: The time for Del is typically between 100 and 500 ms • The cell contents has to be verified (should not be changed) • Above three steps to be done for both states of the every cell Example: MATS+ { (w 0); (r 0, w 1); (r 1, w 0)} becomes { (w 0); Del; (r 0, w 1); Del; (r 1, w 0)} VDD L 1 L 2 DRF Q 6 Q 5 Q 1 BL WL Q 2 VSS BL

6. 1 Pseudo-Random ‘PR’ memory tests • Purpose – – • Explain concept of pseudo-random (PR) testing (1) Compute test length of PR tests for SAFs and k-CFs (5) Evaluation of PR tests (3) PR pattern generators and test response evaluators (2) Sources of material – – – Mazumder, P. and Patel, J. H. (1992). An Efficient Design of Embedded Memories and their Testability Analysis using Markov Chains. JETTA, Vol. 3, No. 3; pp. 235 -250 Krasniewski, A. and Krzysztof, G. (1993). Is There Any Future for Deterministic Self. Test of Embedded RAMs? In Proc. ETC’ 93; pp. 159 -168 van de Goor, A. J. (1998). Testing Semiconductor Memories, Theory and Practice. Com. Tex Publishing, Gouda, The Netherlands van de Goor, A. J. and de Neef, J. (1999). Industrial Evaluation of DRAM Tests. In Proc. Design and Test in Europe (DATe’ 99), March 8 -13, Munich; pp. 623 -630 van de Goor, A. J. and Lin, Mike (1997). The Implementation of Pseudo-Random Tests on Commercial Memory Testers. In Proc. IEEE Int. Test Conf. , Washington DC, 1997, pp. 226 -235

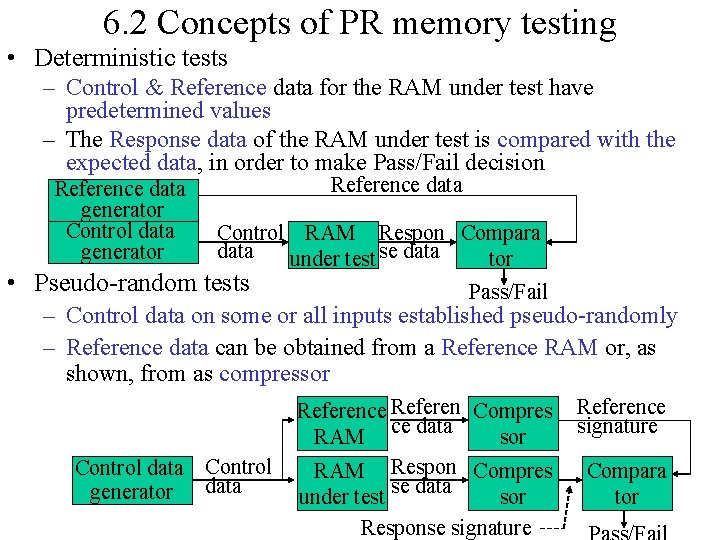
6. 2 Concepts of PR memory testing • Deterministic tests – Control & Reference data for the RAM under test have predetermined values – The Response data of the RAM under test is compared with the expected data, in order to make Pass/Fail decision Reference data generator Control data generator • Reference data Control RAM Respon Compara data under test se data tor Pseudo-random tests Pass/Fail – Control data on some or all inputs established pseudo-randomly – Reference data can be obtained from a Reference RAM or, as shown, from as compressor Control data Control generator data Reference Referen Compres ce data RAM sor RAM Respon Compres se data under test sor Response signature Reference signature Compara tor

6. 3 Concepts of PR memory testing • Memory tests use – control values for: • Address lines (N) • R/W line (1) – write data values (B) • Deterministic test method Address N RAM lines under test R/W line 1 B Data Uses deterministic control and write data values • In a test the following can be Deterministic (D) or PR (R) – The Address (A): DA or RA – The Write (W) operation: DW or RW – The Data (D) to be written: DD or RD MATS+ is a DADWDD (Det. Addr, Det. Write, Det. Data) test • In a PR test at least ONE component has to be PR This can be: A (Addr. ) &/or W (Write oper. ) &/or D (Dat) PR tests are preferred above random tests: PR tests are repeatable

6. 4 Pseudo-random tests for SAFs Some probabilities for computing the test length (TL) – The TL is a function of the escape probability ‘e’ • p: probability that a line has the value 1 • pa: probability that an address line has the value 1 • pd: probability that a data line has the value 1 • pw: probability that the write line has the value 1 • p. A: probability of selecting address A (with z 0 s and N-z 1 s) p. A = (1 - pa)z * pa(N-z) • p 1: probability of writing 1 to address A; p 1 = pd * pw * p. A • p 0: prob. of writing 0 to address A; p 0 =(1 - pd )* pw * p. A • pr: probability of reading address A; pr = (1 - pw )* p. A

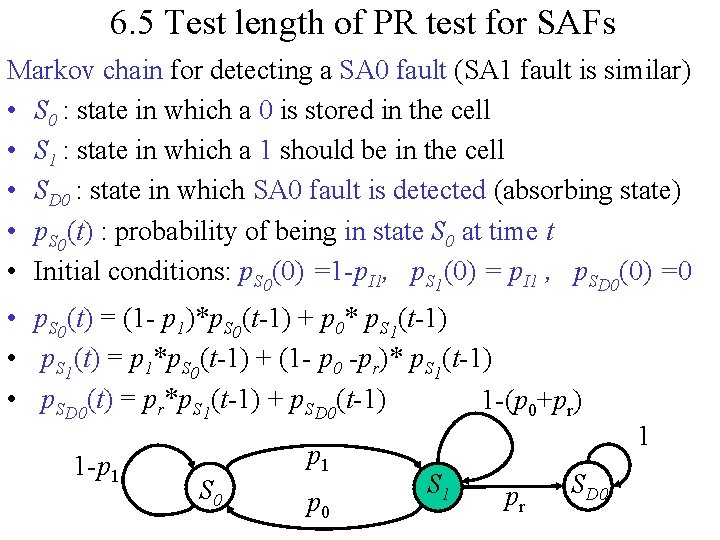
6. 5 Test length of PR test for SAFs Markov chain for detecting a SA 0 fault (SA 1 fault is similar) • S 0 : state in which a 0 is stored in the cell • S 1 : state in which a 1 should be in the cell • SD 0 : state in which SA 0 fault is detected (absorbing state) • p. S 0(t) : probability of being in state S 0 at time t • Initial conditions: p. S 0(0) =1 -p. I 1, p. S 1(0) = p. I 1 , p. SD 0(0) =0 • p. S 0(t) = (1 - p 1)*p. S 0(t-1) + p 0* p. S 1(t-1) • p. S 1(t) = p 1*p. S 0(t-1) + (1 - p 0 -pr)* p. S 1(t-1) • p. SD 0(t) = pr*p. S 1(t-1) + p. SD 0(t-1) 1 -(p 0+pr) 1 -p 1 S 0 p 1 p 0 S 1 pr SD 0 1

6. 6 Test length of PR test for SAFs • • With deterministic testing fault detected with certainty With PR testing fault detected with an escape probability ‘e’ SA 0 fault is detected when: p. SD 0(t) 1 -e; T 0(e) is TL for SA 0 faults T(e): The test length for SAFs is: T(e) = max(T 0(e), T 1(e)) Test length coefficient: Independent of n & proportional with ln(e) Test length coefficient

6. 7 Test length of PR tests for k-CFs PR tests for k-CFids; the k cells may be located anywhere – For k =2 the test will be for CFids; for k >2 the for PSFs – To sensitize the CFid the k-2 cells require enabling value G • For k = 5, there are k-2 = 3 enabling cells CFid 2 • Assume G = 110 = g 1 g 2 g 3 then p. G = pd *(1 -pd) a Several PR tests for k-CFs exist (2 shown below) e • DADWRD (Det. Addr. , Det. Write, PR Data) – Step 1: (w? ); Initialize memory with PR values – Step 2: repeat t times: (r? , w? ); Read and write new PR value – Step 3: (r? ); Perform a final read • RARWRD (PR Addr, PR Write, PR Data) – Step 1: (w 1); Initialize memory – Step 2: repeat t times {Generate PR Addr. , perform read with pr=1 -pw or a write with pw} v e e

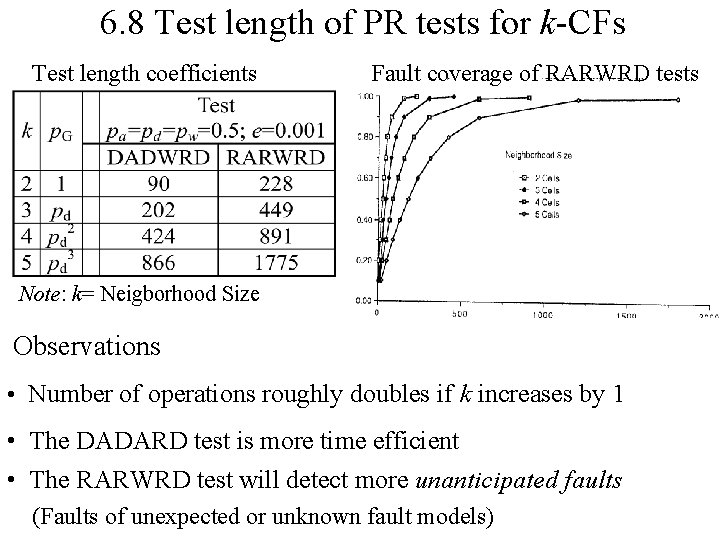
6. 8 Test length of PR tests for k-CFs Test length coefficients Fault coverage of RARWRD tests Note: k= Neigborhood Size Observations • Number of operations roughly doubles if k increases by 1 • The DADARD test is more time efficient • The RARWRD test will detect more unanticipated faults (Faults of unexpected or unknown fault models)

6. 9 Test lengths: Deterministic -- PR tests Observations • Note: ANPSFs have k-2 cells in only one position • For simple fault models deterministic tests more efficient - Detect all faults of some fault models with e = 0 • For complex fault models PR tests do exist - PR tests detect all faults of all fault models, however with e > 0

6. 10 Strengths/weaknesses of PR tests • Deterministic tests based on a-priory fault models – Models usually restricted to the memory cell array – 5% of real defects not explained (Krasniewski, ETC’ 93) – Tests detect 100% of targeted faults only • Pseudo-random tests – Not targeted towards a particular fault model • PR tests detect faults of all fault models; however, with some e > 0 – Long test time: Test length (TL) proportional to ln(e) and 2 k-2 • For CFids: 445*n (e = 10 -5) versus 10*n (for March C-) • Less of a problem for SRAMs (e. g. , 1 Mwrd, 1 ns, 1000 n test takes 1 s) – Random pattern resistant faults • with a large data state (e. g. , bit line imbalance) • requiring a large address/operation state (e. g. , Hammer tests) – Cannot locate faults easily (For laser/dynamic repair) – Well suited for BIST – Very useful for verification purposes – Used for production SRAM testing (together with deterministic tests) • Unknown fault models, short time to volume, high speed SRAM