14 Integers Subunit 1 Positive and Negative Numbers

14. Integers Subunit: 1. Positive and Negative Numbers 2. Addition and subtraction of Integers 3. Multiplication and division of integers

Number line • When points on a line represent numbers, then that line is called number line. -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Definition • Positive number – a number greater than zero. 0 1 2 3 4 5 6

Definition • Negative number – a number less than zero. -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Definition • Opposite Numbers – numbers that are the same distance from zero in the opposite direction -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

Definition • Integers – Integers are all the whole numbers and all of their opposites on the negative number line including zero. 7 opposite -7

Negative Numbers Are Used to Measure Temperature

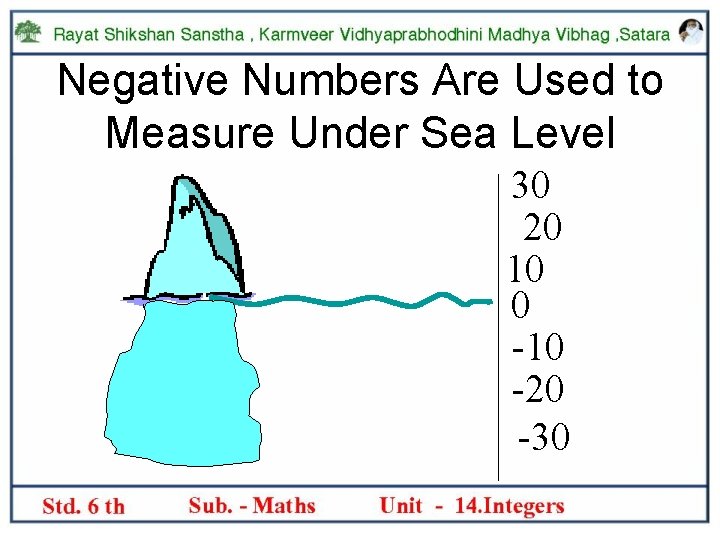
Negative Numbers Are Used to Measure Under Sea Level 30 20 10 0 -10 -20 -30

Hint • If you don’t see a negative or positive sign in front of a number it is positive. +9

14. Integers-2 Subunit: Addition and subtraction of Integers

Addition Rule 1) When the signs are the same, ADD and keep the sign. (-2) + (-4) = -6 2) When the signs are different, SUBTRACT and use the sign of the larger number. (-2) + 4 = 2 2 + (-4) = -2

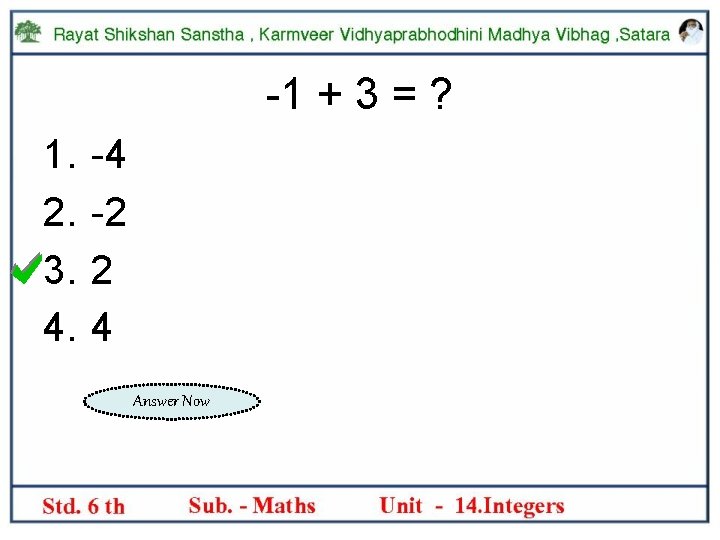
-1 + 3 = ? 1. 2. 3. 4. -4 -2 2 4 Answer Now

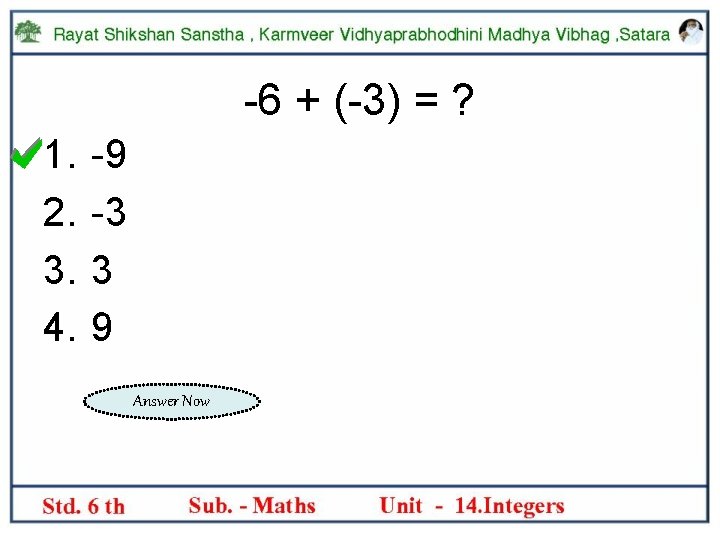
-6 + (-3) = ? 1. 2. 3. 4. -9 -3 3 9 Answer Now

One Way to Add Integers Is With a Number Line When the number is positive count to the right. When the number is negative count to the left. + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6

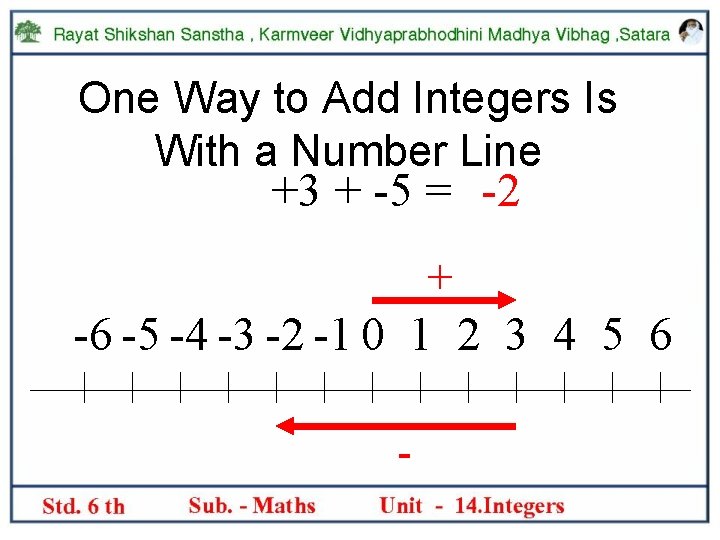
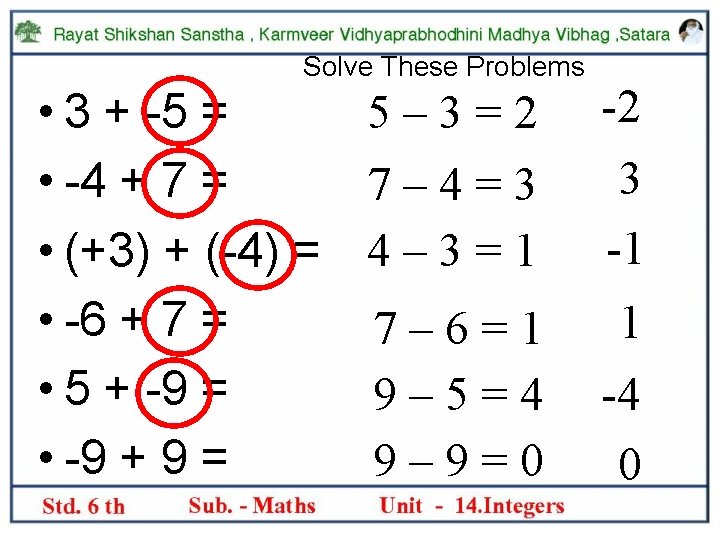
One Way to Add Integers Is With a Number Line +3 + -5 = -2 + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

One Way to Add Integers Is With a Number Line +6 + -4 = +2 + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

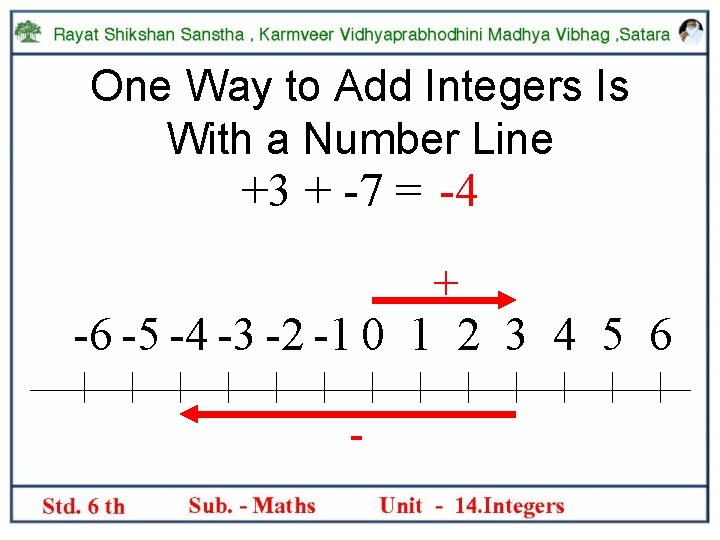
One Way to Add Integers Is With a Number Line +3 + -7 = -4 + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

One Way to Add Integers Is With a Number Line -3 + +7 = +4 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

One Way to Add Integers Is With a Number Line -5 + +3 = +4 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

One Way to Add Integers Is With a Number Line -2 + +8 = +6 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

One Way to Add Integers Is With a Number Line -5 + +2 = -3 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

One Way to Add Integers Is With a Number Line -4 + -2 = -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

One Way to Add Integers Is With a Number Line -2 + -3 = -5 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

One Way to Add Integers Is With a Number Line -1 + -4 = -5 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

One Way to Add Integers Is With a Number Line -4 + -1 = -5 - -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 -

One Way to Add Integers Is With a Number Line 4+1= 5 + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

One Way to Add Integers Is With a Number Line 3+2=5 + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

One Way to Add Integers Is With a Number Line 1+5= 6 + -6 -5 -4 -3 -2 -1 0 1 2 3 4 5 6 +

The additive inverses (or opposites) of two numbers add to equal zero. Example: The additive inverse of 3 is -3 Proof: 3 + (-3) = 0 We will use the additive inverses for subtraction problems.

What’s the difference between 7 - 3 and 7 + (-3) ? 7 - 3 = 4 and 7 + (-3) = 4 The only difference is that 7 - 3 is a subtraction problem and 7 + (3) is an addition problem. “SUBTRACTING IS THE SAME AS ADDING THE OPPOSITE. ”

When subtracting, change the subtraction to adding the opposite and then follow your addition rule. Example #1: - 4 - (-7) - 4 + (+7) Diff. Signs --> Subtract and use larger sign. 3 Example #2: -3 -7 - 3 + (-7) Same Signs --> Add and keep the sign. -10

Okay, here’s one with a variable! Example #3: 11 b - (-2 b) 11 b + (+2 b) Same Signs --> Add and keep the sign. 13 b

1. 2. 3. 4. Which is equivalent to -12 – (-3)? 12 + 3 -12 - 3 Answer Now

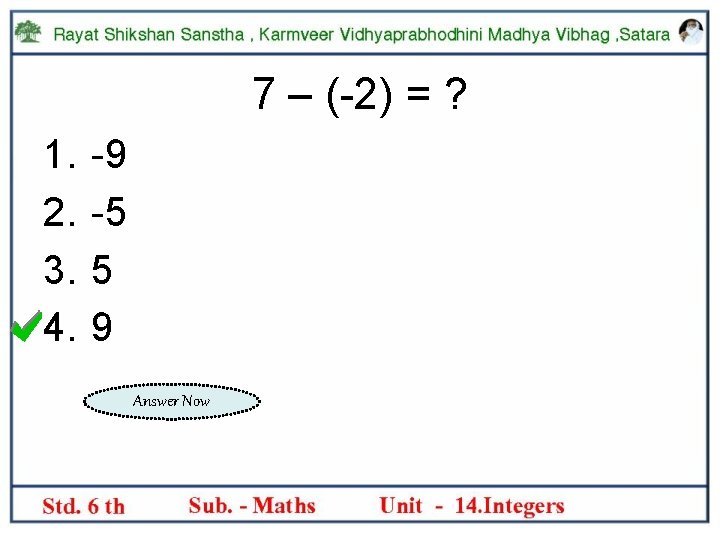
7 – (-2) = ? 1. 2. 3. 4. -9 -5 5 9 Answer Now

Operations with Integers

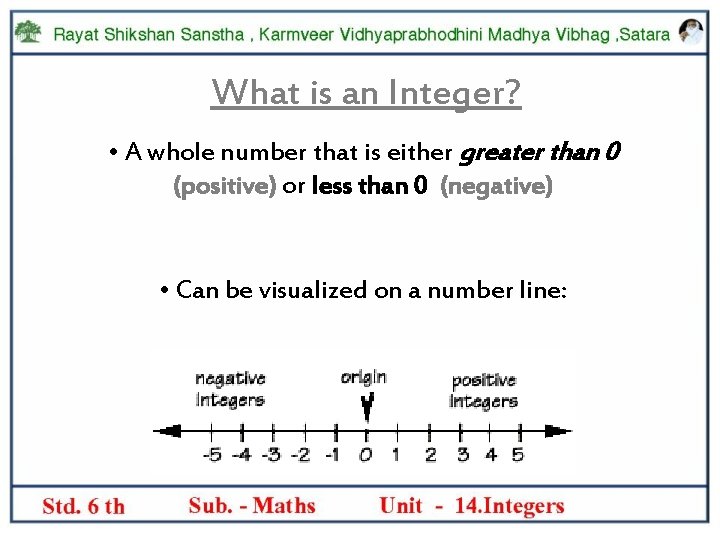
What is an Integer? • A whole number that is either greater than 0 (positive) or less than 0 (negative) • Can be visualized on a number line:

What is a Number Line? • A line with arrows on both ends that show the integers with slash marks • Arrows show the line goes to infinity in both directions ( + and -) • Uses a negative sign (-) with negative numbers but no positive sign (+) with positive numbers • Zero is the origin and is neither positive negative nor

What are Opposites? • Two integers the same distance from the origin, but on different sides of zero • Every positive integer has a negative integer an equal distance from the origin • Example: The opposite of 6 is -6 • Example: The opposite of -2 is 2

What is Absolute Value? • Distance a number is from zero on a number line (always a positive number) • Indicated by two vertical lines | | • Every number has an absolute value • Opposites have the same absolute values since they are the same distance from zero Example: |-8| = 8 and |8| = 8 • Example: |50| = 50 and |-50| = 50

What Can We Do to Integers? • Integers are numbers, so we can add, multiply, and divide them subtract, • Each operation has different rules to follow

Adding Rules – Same Signs • If the integers have the SAME signs: ADD the numbers & keep the same sign! • Positive + Positive = Positive Answer • Negative + Negative = Negative Answer • Examples: -3 + (-10) = ? ? = -13 • 6 + (8) = ? ? = 14

Adding (Same Signs) - Examples #1. -3 + (-10) Step 1: 13 Step 2: -13 Add the #s Keep same sign (Both #s are negative – Answer is negative!) #2. 6 + (8) Step 1: 14 Step 2: 14 Add the #s Keep same sign (Both #s are positive – Answer is positive!)

Adding Rules – Different Signs • If the integers have the DIFFERENT signs: SUBTRACT the numbers & use sign of the BIGGER number! • Bigger # is Positive = Positive Answer • Bigger # is Negative = Negative Answer • Examples: -13 + (7) = ? ? = -6 • 23 + (-8) = ? ? = 15

#1. -13 + (7) Step 1: Step 2: 6 Subtract the #s -6 Use sign of bigger # (Bigger # is negative - Answer is negative!) #2. 23 + (-8) Step 1: 15 Step 2: 15 Subtract the #s Use sign of bigger # (Bigger # is positive - Answer is positive!)

Subtracting Rules • Put ( ) around second number & its sign • Change SUBTRACTION sign to an ADDITION sign • Change sign of 2 nd number to its opposite • Follow the rules for ADDITION: -SAME signs: Add & keep the same sign -DIFFERENT signs: Subtract & use sign of bigger # • Examples: -5 – -10 = ? ? = 5 • 9 - 23 = ? ? = -14

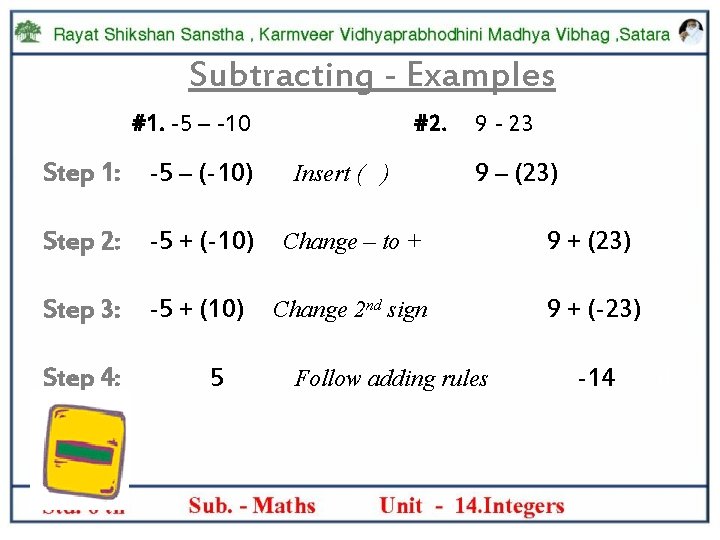
Subtracting - Examples #1. -5 – -10 #2. 9 - 23 Step 1: -5 – (-10) Step 2: -5 + (-10) Change – to + 9 + (23) Step 3: -5 + (10) Change 2 nd sign 9 + (-23) Step 4: 5 Insert ( ) 9 – (23) Follow adding rules -14 d

Multiplying Rules • Multiply the numbers like usual • If the integers have the SAME signs: ANSWER will be POSITIVE • If the integers have DIFFERENT signs: ANSWER will be NEGATIVE • Examples: -3 · (-5) = ? ? = 15 -9 · (-10) = ? ? = 90 • • -7 · 7 = ? • 6 · -6 = ? ? = -36 ? = -49

Multiplying - Examples • #1. -3 · (-5) #2. -9 · (-10) • 15 Multiply the numbers • 15 Same signs = Positive Answer #3. -7 · 7 49 -49 90 90 #4. 6 · -6 Multiply the numbers Different signs = Negative Answer 36 -36

Dividing Rules • Divide the numbers like usual • If the integers have the SAME signs: ANSWER will be POSITIVE • If the integers have DIFFERENT signs: ANSWER will be NEGATIVE • Examples: -33 ÷ (-3) = ? ? = 11 -90 ÷ (-10) = ? ? = 9 • • -20 ÷ 2 = ? • 6 ÷ -6 = ? ? = -10

Dividing - Examples • #1. -33 ÷ (-3) #2. -90 ÷ (-10) • 11 Divide the numbers • 11 Same signs = Positive Answer #3. -20 ÷ 2 10 -10 9 9 #4. 6 ÷ -6 1 Divide the numbers Different signs = Negative Answer -1

Mixed Practice Solve the following problems: -9 + - 9 7 · -4 -18 -28 -35 ÷ -7 15 + -25 5 -10 - (-19) 9 -23 - 9 -32

• Created By –