14 Bessel Functions 1 Bessel Functions of the

14. Bessel Functions 1. Bessel Functions of the 1 st Kind, J (x) 2. Orthogonality 3. Neumann Functions, Bessel Functions of the 2 nd Kind 4. Hankel Functions, I (x) and K (x) 5. Asymptotic Expansions 6. Spherical Bessel Functions

Defining Properties of Special Functions 1. Differential eq. 2. Series form / Generating function. 3. Recurrence relations. 4. Integral representation. Basic Properties : 1. Orthonormality. 2. Asymptotic form. Ref : 1. M. Abramowitz & I. A. Stegun, Handbook of Mathematical Functions, Dover Publ. (1970) http: //people. math. sfu. ca/~cbm/aands/abramowi 2. tz_and_stegun. pdf. NIST Digital Library of Mathematical Functions: http: //dlmf. nist. gov/

Usage of Bessel Functions Solutions to equations involving the Laplacian, 2 , in or circular cylindrical coordinates : Bessel / Modified Bessel functions spherical coordinates : Spherical Bessel functions

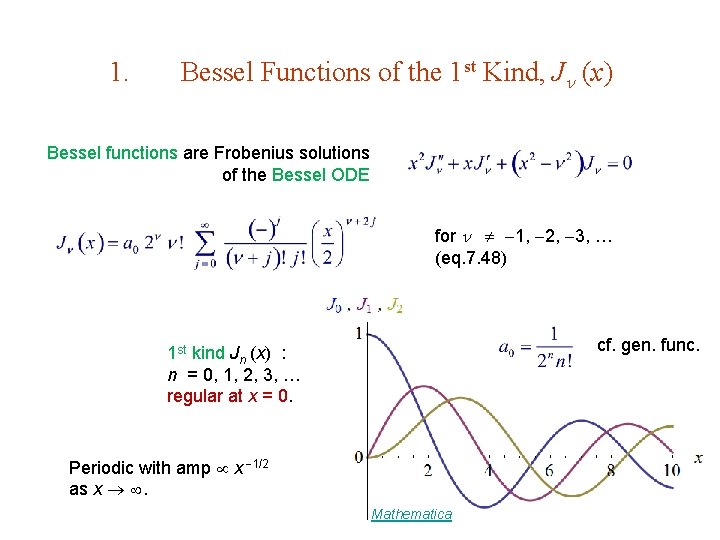
1. Bessel Functions of the 1 st Kind, J (x) Bessel functions are Frobenius solutions of the Bessel ODE for 1, 2, 3, … (eq. 7. 48) cf. gen. func. 1 st kind Jn (x) : n = 0, 1, 2, 3, … regular at x = 0. Periodic with amp x 1/2 as x . Mathematica

Generating Function for Integral Order Generating function : For n 0 ( n = m < 0 : Generalize: in eq. 7. 48 )

Recurrence

Ex. 14. 1. 4

Bessel’s Differential Equation Any set of functions Z (x) satisfying the recursions must also satisfy the ODE, though not necessarily the series expansion. Proof :

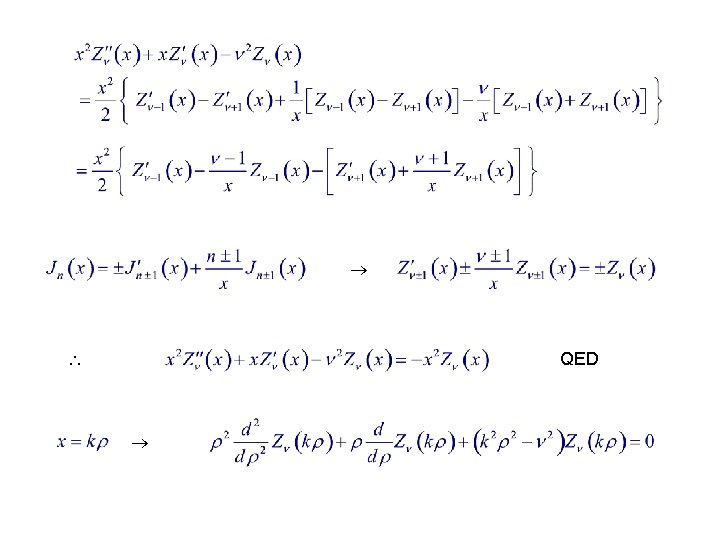
QED

Integral Representation : Integral Order C encloses t = 0. n = integers C = unit circle centered at origin : Re : Im : n = integers

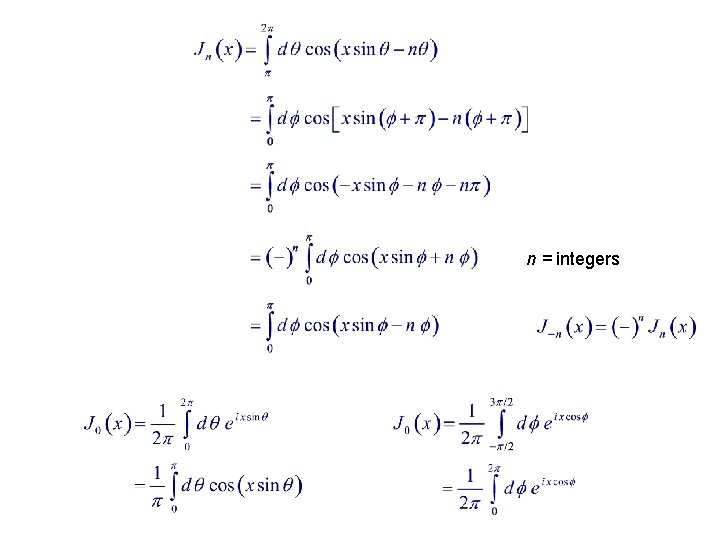
n = integers

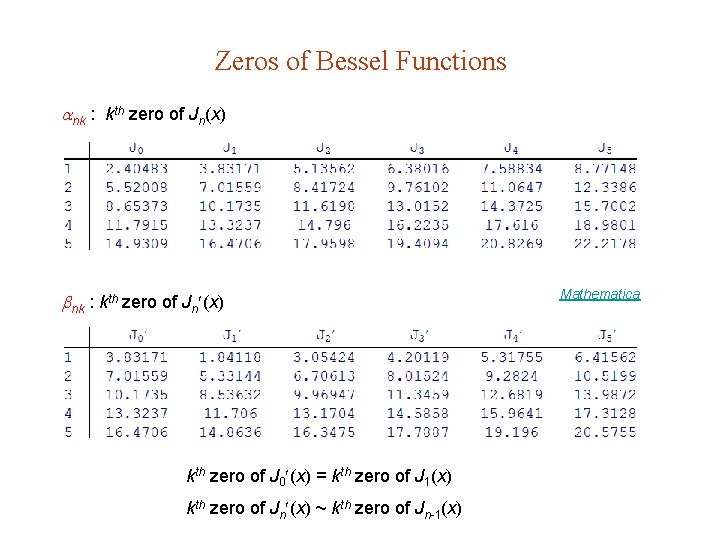
Zeros of Bessel Functions nk : kth zero of Jn(x) nk : kth zero of Jn (x) kth zero of J 0 (x) = kth zero of J 1(x) kth zero of Jn (x) ~ kth zero of Jn-1(x) Mathematica

Example 14. 1. 1. Fraunhofer Diffraction, Circular Aperture Kirchhoff's diffraction formula (scalar amplitude of field) : Fraunhofer diffraction (far field) for incident plane wave, circular aperture : Mathematica

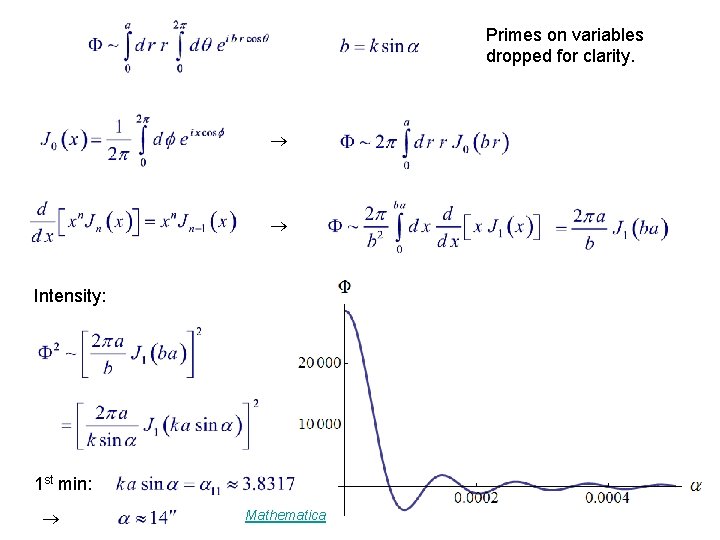
Primes on variables dropped for clarity. Intensity: 1 st min: Mathematica

Example 14. 1. 2. Cylindrical Resonant Cavity Wave equation in vacuum : Circular cylindrical cavity, axis along z-axis : // means tangent to wall S TM mode :

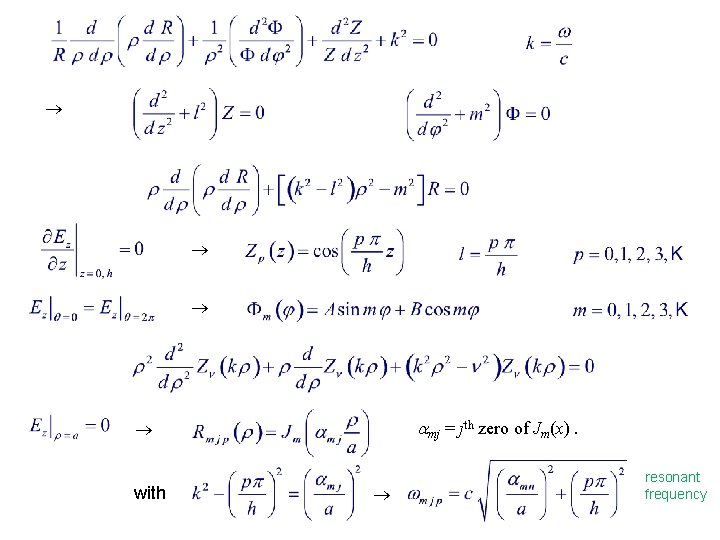
mj = jth zero of Jm(x). with resonant frequency

Bessel Functions of Nonintegral Order Formally, gives only Jn of integral order. with However, the series expansion can be extended to J of nonintegral order : for 1, 2, 3, … Caution: are linearly independent.

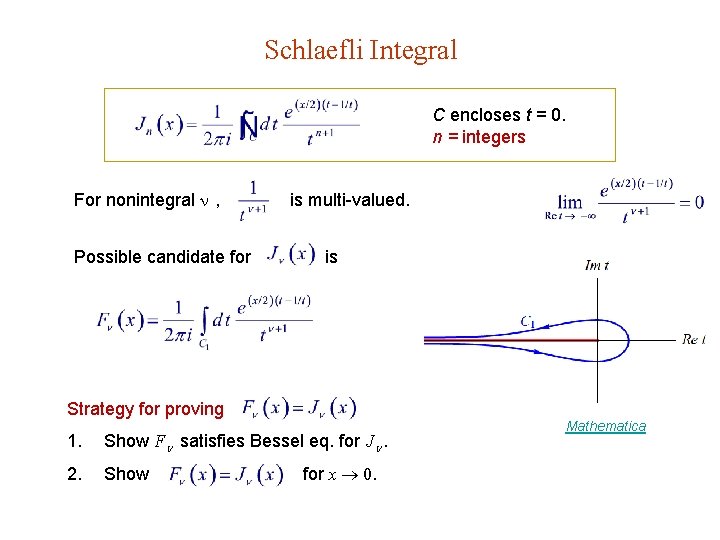
Schlaefli Integral C encloses t = 0. n = integers For nonintegral , Possible candidate for is multi-valued. is Strategy for proving 1. Show F satisfies Bessel eq. for J . 2. Show for x 0. Mathematica

Consider any open contour C that doesn’t cross the branch cut

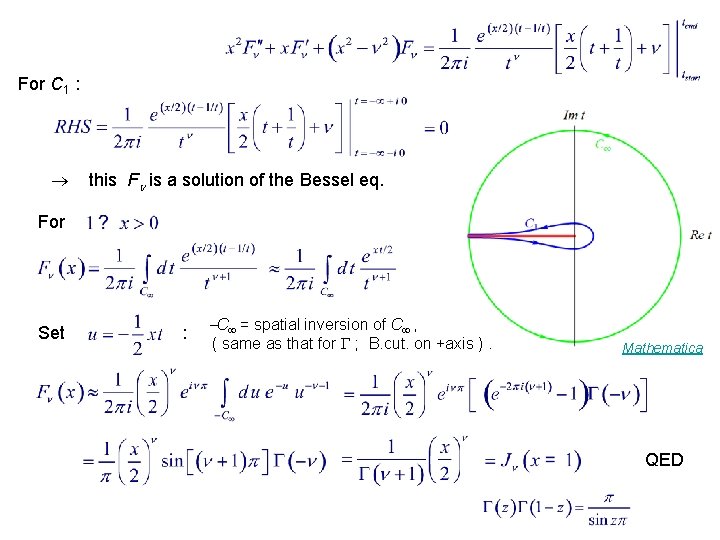
For C 1 : this F is a solution of the Bessel eq. For Set : C = spatial inversion of C , ( same as that for ; B. cut. on +axis ). Mathematica QED

2. Orthogonality where i. e. , Z (k ) is the eigenfunction, with eigenvalue k 2 , of the operator L . ( Sturm-Liouville eigenvalue probem ) Helmholtz eq. in cylindrical coordinates with mn = nth root of Jm

is not self-adjoint is self-adjoint L is Hermitian, i. e. , J is an eigenfunction of L with eigenvalue k 2. , if the inner product is defined as

Orthogonal Sets Let Orthogonality : orthogonal set

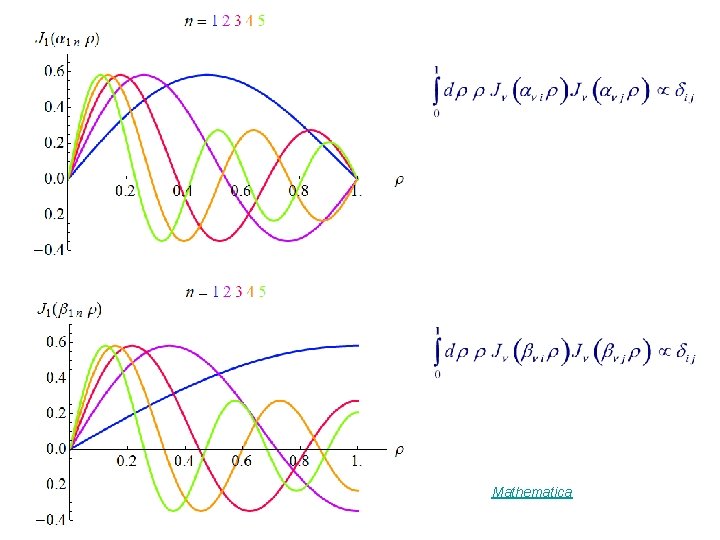
Mathematica

Normalization

Mathematica Similarly : (see Ex. 14. 2. 2)

Bessel Series : J ( i / a ) For any well-behaved function f ( ) with f (a) 0 : for any > 1 with

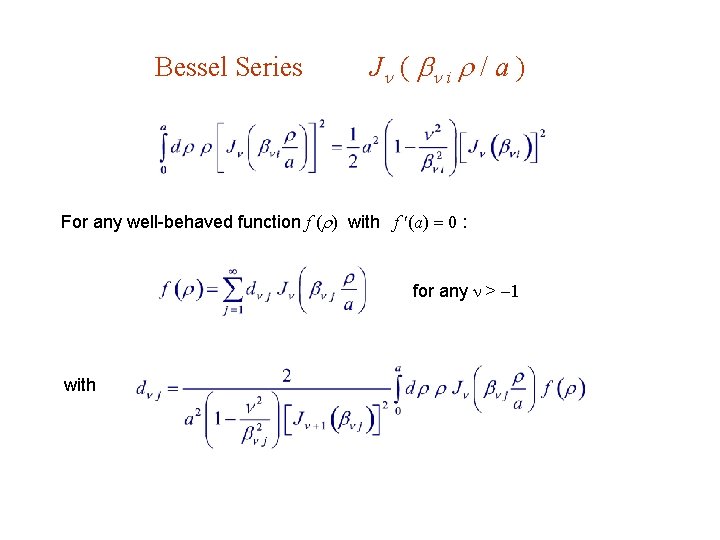
Bessel Series J ( i / a ) For any well-behaved function f ( ) with f (a) 0 : for any > 1 with

Example 14. 2. 1. Electrostatic Potential: Hollow Cylinder Hollow cylinder : axis // z-axis, ends at z = 0, h ; radius = a. Potentials at boundaries : Electrostatics, no charges : Eigenstates with cylindrical symmetry :

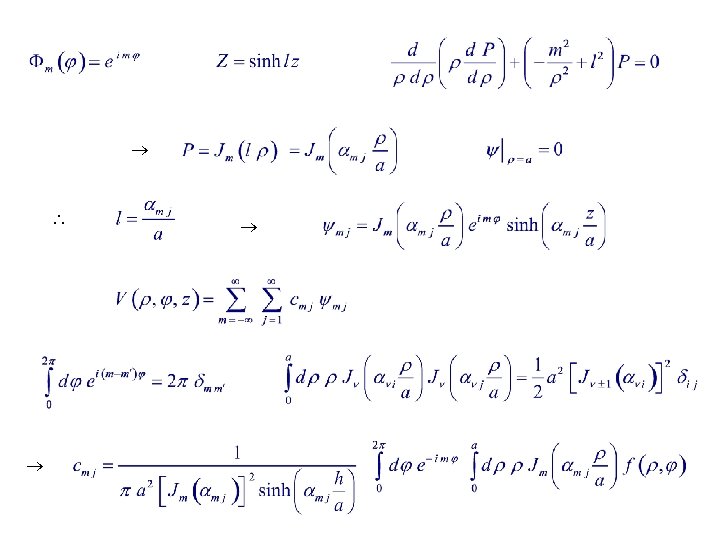
3. Neumann Functions, Bessel Functions of the 2 nd Kind Neumann Functions : x << 1

Ex. 14. 3. 8 x << 1 agrees with

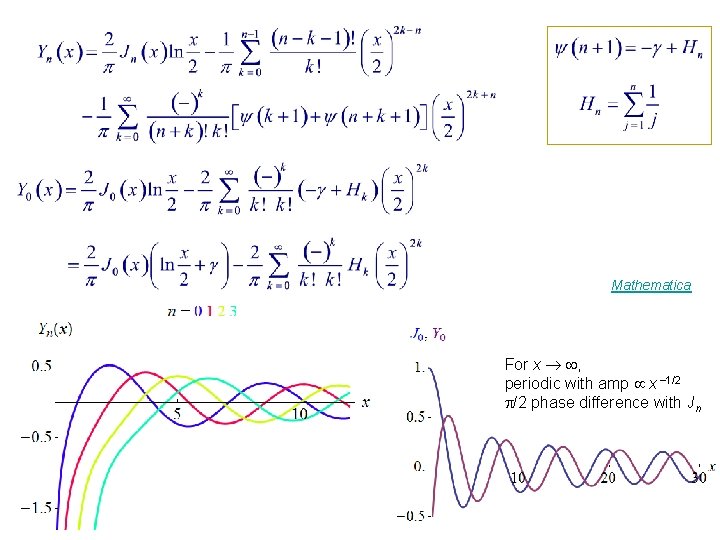
Mathematica For x , periodic with amp x 1/2 /2 phase difference with Jn

Integral Representation Ex. 14. 3. 7 Ex. 14. 4. 8

Recurrence Relations

Since Y satisfy the same RRs for J , they are also the solutions to the Bessel eq. Caution: Since RR relates solutions to different ODEs (of different ), it depends on their normalizations.

Wronskian Formulas For an ODE in self-adjoint form the Wronskian of any two solutions satisfies Bessel eq. in self-adjoint form : For a noninteger , the two independent solutions J & J satisfy Ex. 7. 6. 1

A can be determined at any point, such as x = 0.

More Recurrence Relations Combining the Wronskian with the previous recurrence relations, one gets many more recurrence relations

Uses of Neumann Functions 1. Complete the general solutions. 2. Applicable to any region excluding the origin ( e. g. , coaxial cable, quantum scattering ). 3. Build up the Hankel functions ( for propagating waves ).

Example 14. 3. 1. Coaxial Wave Guides EM waves in region between 2 concentric cylindrical conductors of radii a & b. ( c. f. , Eg. 14. 1. 2 & Ex. 14. 1. 26 ) For TM mode in cylindrical cavity (eg. 14. 1. 2) : For TM mode in coaxial cable of radii a & b : with Note: No cut-off for TEM modes.