14 Bessel Functions 1 Bessel Functions of the

14. Bessel Functions 1. Bessel Functions of the 1 st Kind, J (x) 2. Orthogonality 3. Neumann Functions, Bessel Functions of the 2 nd Kind 4. Hankel Functions, I (x) and K (x) 5. Asymptotic Expansions 6. Spherical Bessel Functions

Defining Properties of Special Functions 1. Differential eq. 2. Series form / Generating function. 3. Recurrence relations. 4. Integral representation. Basic Properties : 1. Orthonormality. 2. Asymptotic form. Ref : 1. M. Abramowitz & I. A. Stegun, Handbook of Mathematical Functions, Dover Publ. (1970) http: //people. math. sfu. ca/~cbm/aands/abramowi 2. tz_and_stegun. pdf. NIST Digital Library of Mathematical Functions: http: //dlmf. nist. gov/

Usage of Bessel Functions Solutions to equations involving the Laplacian, 2 , in or circular cylindrical coordinates : Bessel / Modified Bessel functions spherical coordinates : Spherical Bessel functions
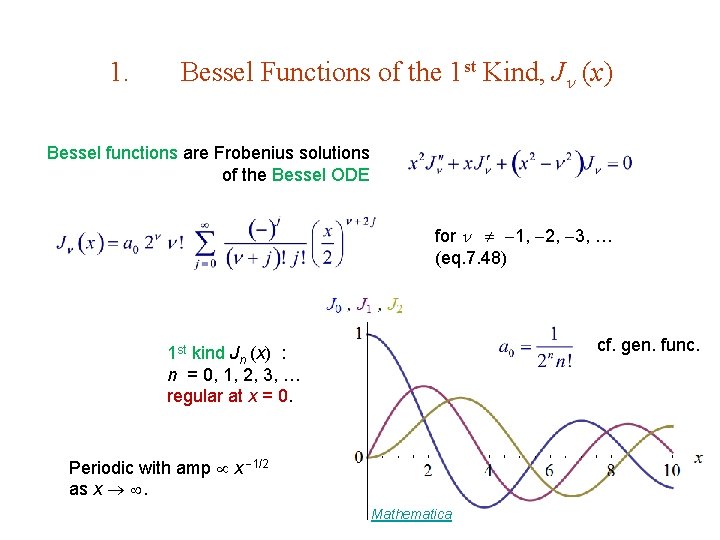
1. Bessel Functions of the 1 st Kind, J (x) Bessel functions are Frobenius solutions of the Bessel ODE for 1, 2, 3, … (eq. 7. 48) cf. gen. func. 1 st kind Jn (x) : n = 0, 1, 2, 3, … regular at x = 0. Periodic with amp x 1/2 as x . Mathematica

Generating Function for Integral Order Generating function : For n 0 ( n = m < 0 : Generalize: in eq. 7. 48 )

Recurrence

Ex. 14. 1. 4

Bessel’s Differential Equation Any set of functions Z (x) satisfying the recursions must also satisfy the ODE, though not necessarily the series expansion. Proof :
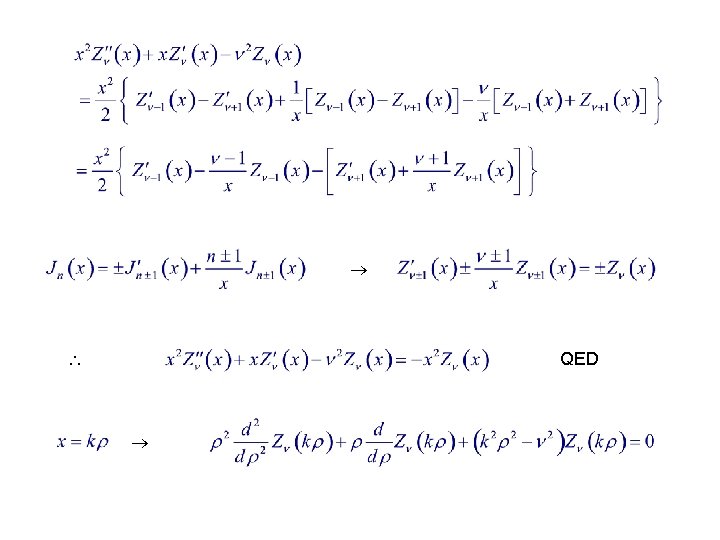
QED

Integral Representation : Integral Order C encloses t = 0. n = integers C = unit circle centered at origin : Re : Im : n = integers
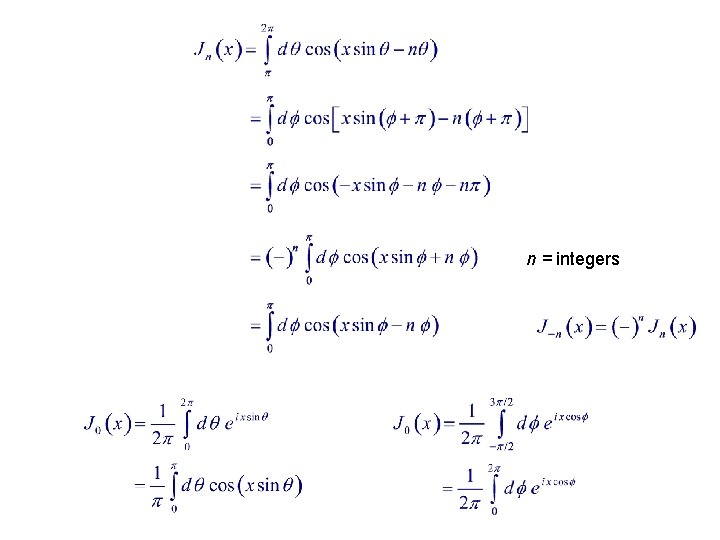
n = integers
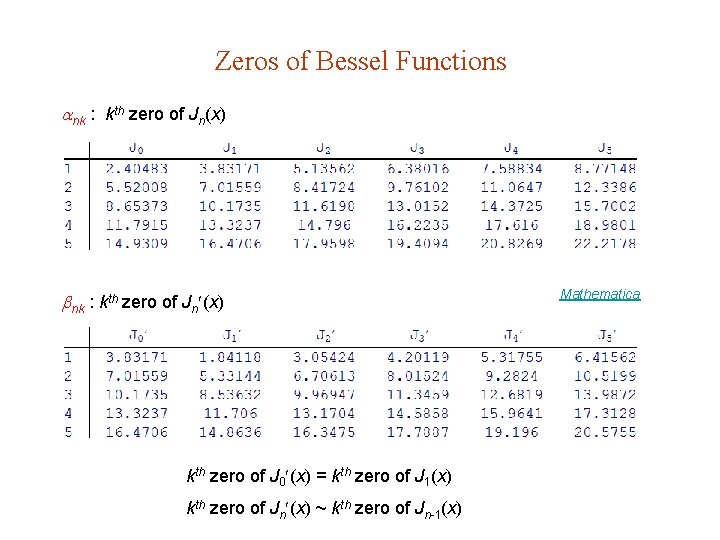
Zeros of Bessel Functions nk : kth zero of Jn(x) nk : kth zero of Jn (x) kth zero of J 0 (x) = kth zero of J 1(x) kth zero of Jn (x) ~ kth zero of Jn-1(x) Mathematica

Example 14. 1. 1. Fraunhofer Diffraction, Circular Aperture Kirchhoff's diffraction formula (scalar amplitude of field) : Fraunhofer diffraction (far field) for incident plane wave, circular aperture : Mathematica
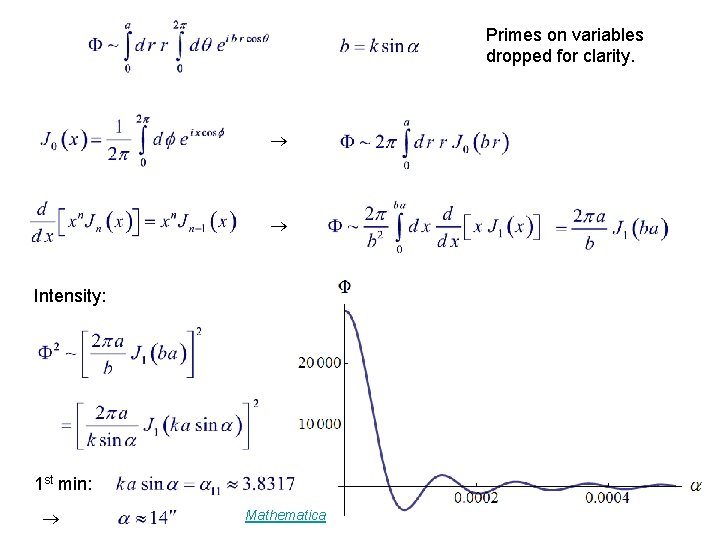
Primes on variables dropped for clarity. Intensity: 1 st min: Mathematica

Example 14. 1. 2. Cylindrical Resonant Cavity Wave equation in vacuum : Circular cylindrical cavity, axis along z-axis : // means tangent to wall S TM mode :
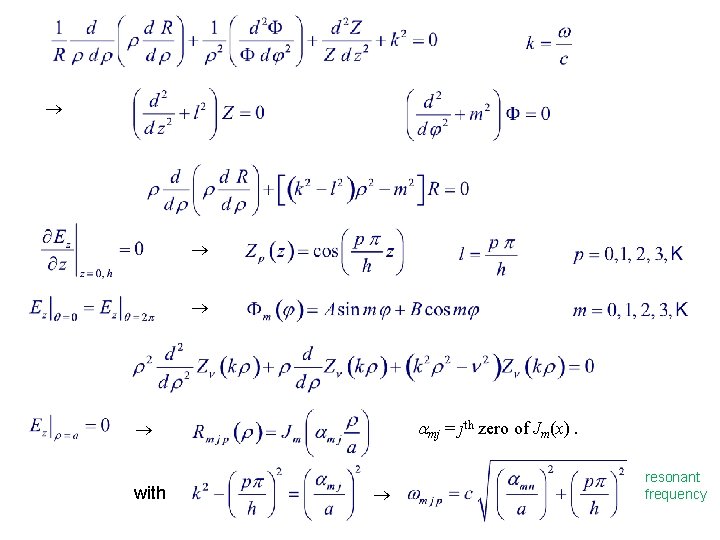
mj = jth zero of Jm(x). with resonant frequency

Bessel Functions of Nonintegral Order Formally, gives only Jn of integral order. with However, the series expansion can be extended to J of nonintegral order : for 1, 2, 3, … Caution: are linearly independent.
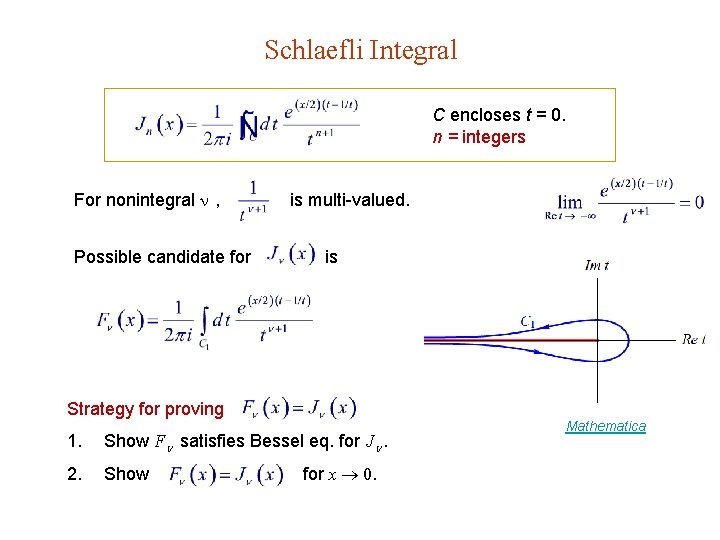
Schlaefli Integral C encloses t = 0. n = integers For nonintegral , Possible candidate for is multi-valued. is Strategy for proving 1. Show F satisfies Bessel eq. for J . 2. Show for x 0. Mathematica

Consider any open contour C that doesn’t cross the branch cut
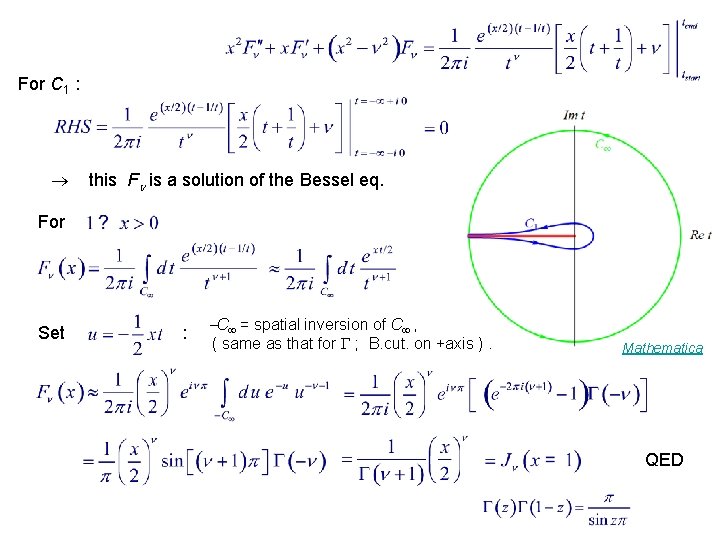
For C 1 : this F is a solution of the Bessel eq. For Set : C = spatial inversion of C , ( same as that for ; B. cut. on +axis ). Mathematica QED

2. Orthogonality where i. e. , Z (k ) is the eigenfunction, with eigenvalue k 2 , of the operator L . ( Sturm-Liouville eigenvalue probem ) Helmholtz eq. in cylindrical coordinates with mn = nth root of Jm

is not self-adjoint is self-adjoint L is Hermitian, i. e. , J is an eigenfunction of L with eigenvalue k 2. , if the inner product is defined as


Orthogonal Sets Let Orthogonality : orthogonal set
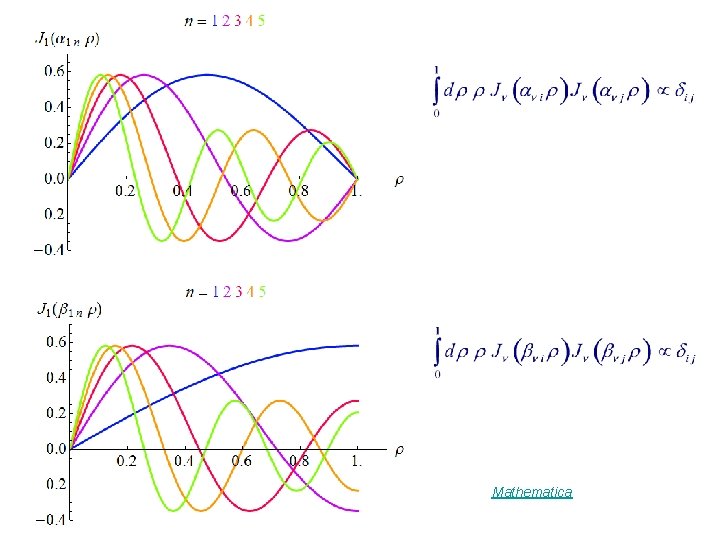
Mathematica

Normalization

Mathematica Similarly : (see Ex. 14. 2. 2)

Bessel Series : J ( i / a ) For any well-behaved function f ( ) with f (a) 0 : for any > 1 with
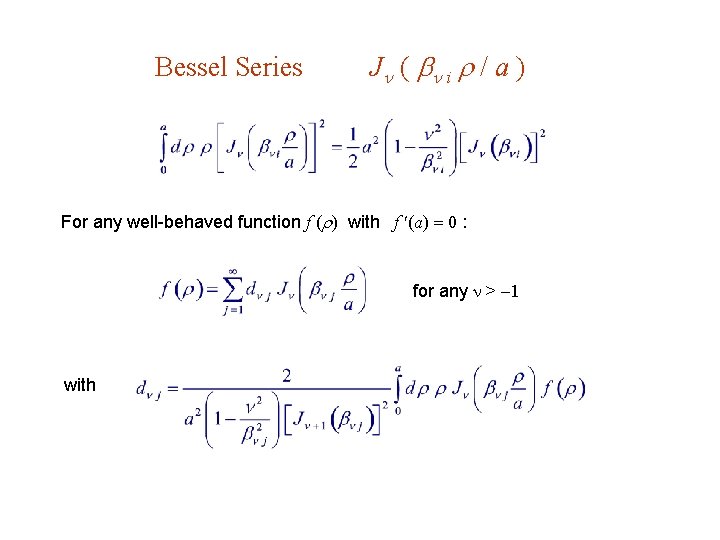
Bessel Series J ( i / a ) For any well-behaved function f ( ) with f (a) 0 : for any > 1 with

Example 14. 2. 1. Electrostatic Potential: Hollow Cylinder Hollow cylinder : axis // z-axis, ends at z = 0, h ; radius = a. Potentials at boundaries : Electrostatics, no charges : Eigenstates with cylindrical symmetry :
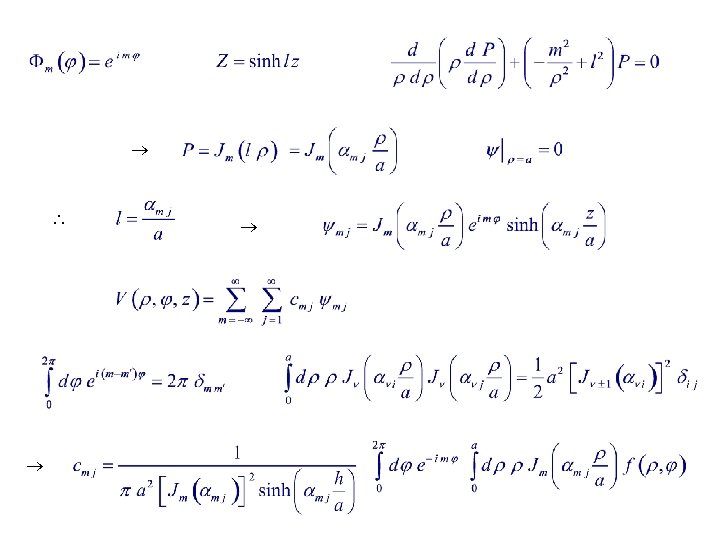
- Slides: 31