14 11 2016 Chu Shih Chieh Zhu Shijie



















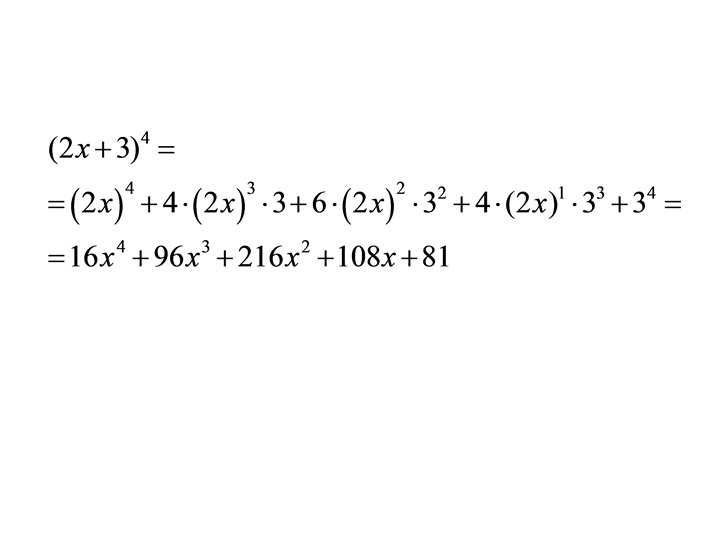









- Slides: 33

14. 11. 2016

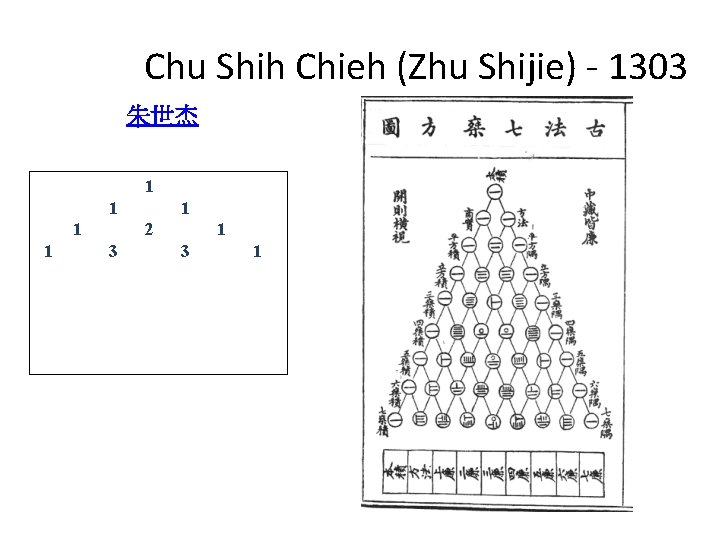
Chu Shih Chieh (Zhu Shijie) - 1303 朱世杰 1 1 1 2 3 1

Pascali kolmnurk (1653) 1 1 1 1 1 8 3 5 7 6 15 1 4 10 20 35 56 1 3 10 21 28 2 4 6 1 5 15 35 70 1 1 6 21 56 1 7 28 1

Pascali kolmnurk kombinatsioonidena

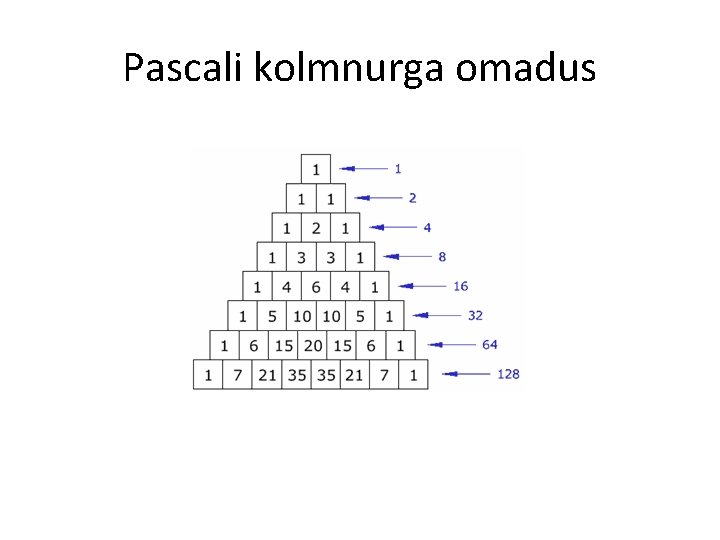
Pascali kolmnurga omadus

Newtoni binoomvalem Teatavasti: (a+b)0 = 1 (a+b)1 = a + b = 1 a + 1 b (a+b)2 = a 2 + 2 ab + b 2 = 1 a 2 + 2 ab + 1 b 2 (a+b)3 = a 3 + 3 a 2 b + 3 ab 2 + b 3 = = 1 a 3 + 3 a 2 b + 3 ab 2 + 1 b 3 Kirjutades välja kordajad, saame Pascali kolmnurga!

Newtoni binoomvalem Kordajad saame Pascali kolmnurgast, muutujate astmed: a astendajad vähenevad b astendajad suurenevad a ja b astendajate summa on n

Harjutus Kirjutada välja (x + y)4 = (a + b)5 =

Harjutus Kirjutada välja (x + y)4 = x 4 + 4 x 3 y + 6 x 2 y 2 + 4 xy 3 + y 4 (a + b)5 = =a 5 + 5 a 4 b + 10 a 3 b 2 + 10 a 2 b 3 + 5 ab 4 + b 5 Kuidas toimida, kui sulgudes on negatiivne liige?

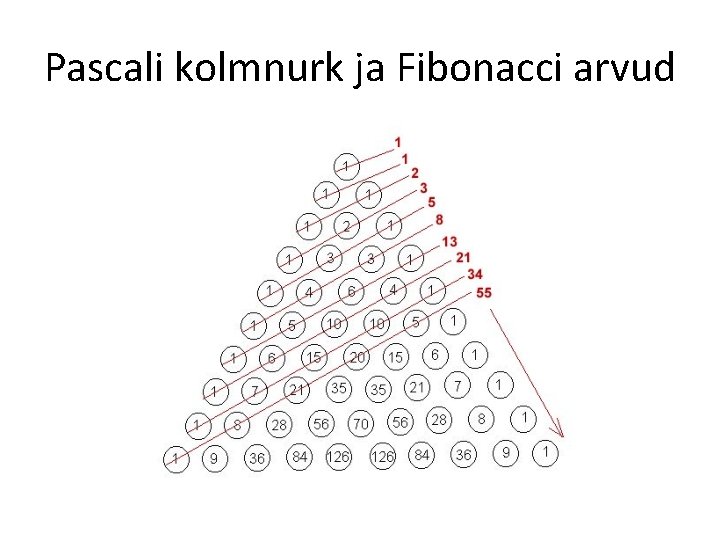
Fibonacci arvud Vaatleme arvujada 1; 1; 2; 3; 5; 8; 13; … Jada iga liige (alates 3. liikmest) on kahe eelneva liikme summa. Sellist jada nimetatakse Fibonacci jadaks (kirjeldatud aastal 1202)

Pascali kolmnurk ja Fibonacci arvud

Turku Energia OY korsten

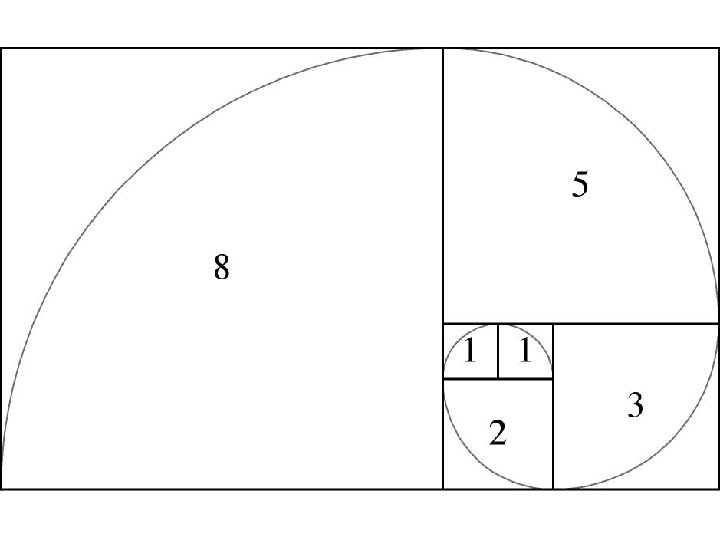
Fibonacci spiraal

Fibonacci spiraal looduses


Näited Fibonacci arvude kohta

XX. 11. 2016 • • Pascali kolmnurk Newtoni binoomvalem Riigieksamilt 2015 De Méré ülesande lahendus

Tegevus nr 1 Kirjutada välja Pascali kolmnurk, milles on vähemalt 7 -8 rida. Aega on 60 sekundit.

Pascali kolmnurk 1 1 1 1 1 8 3 5 7 6 15 1 4 10 20 35 56 1 3 10 21 28 2 4 6 1 5 15 35 70 1 1 6 21 56 1 7 28 1

Newtoni binoomvalem Kordajad saame Pascali kolmnurgast, muutujate astmed: a astendajad vähenevad b astendajad suurenevad a ja b astendajate summa on n

Lahendusskeem 1 1 1 2 3 1 (x + 3)3 = 1 x 3 + 3 x 2 3 + 3 x 32 + 1 33 = = x 3 + 9 x 2 +27 x + 27

Ülesanne 1 Koostada Pascali kolmnurk ning avaldada selle abil (a + 2)5 = (2 x + 3)4 = (x – 4 y)4 =

Ülesanne 1 (lahendus) Koostada Pascali kolmnurk ning avaldada selle abil
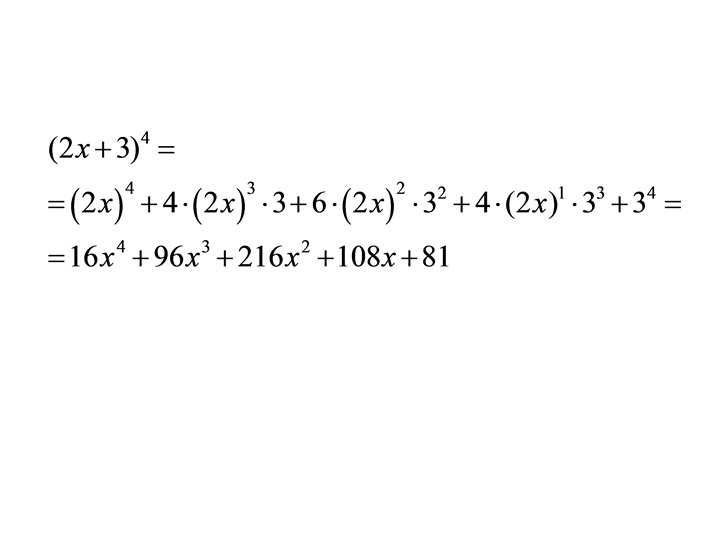


Riigieksami ülesanne aastast 2015 Karbis on rohelised ja punased pliiatsid, kokku 27 pliiatsit. Valides ühe juhusliku pliiatsi, on punase pliiatsi saamise tõenäosus. 1. Mitu punast ja mitu rohelist pliiatsis on karbis? 2. Arvutada järgmiste sündmuste tõenäosus: 1) üks juhuslikult valitud pliiats on roheline; 2) kaks juhuslikult valitud pliiatsit on mõlemad punased

Võimalik lahendus 1. Olgu punaste pliiatsite arv x. Siis tõenäosus saada punane pliiats on • Kuna see tõenäosus on teada, siis saame: • Seega karbis on 12 punast ja 15 rohelist pliiatsit.

(lahenduse jätk) 2. Leiame vastavad tõenäosused: 1) (rohelise pliiatsi saamise tõenäosus): 2) (saadakse kaks punast pliiatsit):

De Méré ülesanne Võrdsete võimalustega mängu mängitakse 5 võiduni. Mängija A on võitnud 3 mängu, mängija B on võitnud 2 mängu. Kui mäng katkestatakse, millises suhtes tuleks panused jaotada?

Méré ülesande lahendus (Fermat) A võidab Seis on 5: 2 A võidab Seis on 5: 3 A võidab Seis on 4: 2 B võidab A võidab Seis on 5: 4 Seis on 4: 3 B võidab Seis on 4: 4 B võidab Seis on 4: 5 Algus; seis on 3: 2 A – vaja 2 võitu A võidab Seis on 5: 3 B – vaja 3 võitu A võidab Seis on 4: 3 A võidab Seis on 5: 4 B võidab Seis on 4: 5 B võidab Seis on 3: 3 A võidab Seis on 5: 4 A võidab Seis on 4: 4 B võidab Seis on 3: 4 B võidab Seis on 4: 5 B võidab Seis on 3: 5 A võit: B võit:

Võitude suhe (selles suhtes tuleb jagada panused):

De Méré probleemi lahendus Pascali kolmnurga abil Panuste suhe: (1 + 4 + 6) : (4 + 1) = 11 : 5

Ülesanne Mängitakse 6 võiduni. Mängijal A on vaja saada 2 võitu, mängijal B 4 võitu. Kui suur on mängijate võitude tõenäosuste suhe p(A) : p(B)? /kasutada Pascali kolmnurka võitude puud/
 Chu shih-chieh
Chu shih-chieh Shih-chieh hsu
Shih-chieh hsu Lean office definition
Lean office definition Trò chơi chữ cái u ư chủ đề nghề nghiệp
Trò chơi chữ cái u ư chủ đề nghề nghiệp Muốn tính chu vi hình chữ nhật
Muốn tính chu vi hình chữ nhật Cách tính chu vi hình tam giác
Cách tính chu vi hình tam giác Arus pu chu chu
Arus pu chu chu Tzu chieh wei
Tzu chieh wei Nonepileptiform
Nonepileptiform Supperprof
Supperprof Unang banyagang dinastiya ng china
Unang banyagang dinastiya ng china 您vs你
您vs你 Lim shih hui
Lim shih hui Shih chao-hwei
Shih chao-hwei Uiuc ealc
Uiuc ealc Yüan-shih t'ien-tsun
Yüan-shih t'ien-tsun Moodle taylors
Moodle taylors Chilin shih
Chilin shih Man wo
Man wo Zhu rongji
Zhu rongji Zhu ci
Zhu ci Kerry zhu
Kerry zhu Xuding zhu
Xuding zhu Xianli zhu
Xianli zhu Zhe yi sheng zui mei de zhu fu lyrics
Zhe yi sheng zui mei de zhu fu lyrics Mechanical engineering umbc
Mechanical engineering umbc Berquist sherman method
Berquist sherman method Axing zhu
Axing zhu Edward zhu
Edward zhu Dou mei zhu
Dou mei zhu Zhu shi
Zhu shi Haibin zhu
Haibin zhu Internationalization testing checklist
Internationalization testing checklist Weimo zhu
Weimo zhu