13 January 2022 The fundamental theorem of Algebra

13 January 2022 The fundamental theorem of Algebra (FTA) LO: To know and use the fundamental theorem of algebra. www. mathssupport. org

The fundamental theorem of algebra. A polynomial f(x) = anxn + an-1 xn-1 + an-2 xn-2 + … + a 2 x 2 + a 1 x + a 0 With real or complex coefficients (an ≠ 0) has at least one zero. There is an w ℂ such that f(w) = 0 Corollary: Each polynomial f(x) = anxn + an-1 xn-1 + an-2 xn-2 + … + a 2 x 2 + a 1 x + a 0 With real or complex coefficients can be written in f(x) = an(x – w 1) (x – w 2) … (x – wn) a factored form Such that wk ℂ, k = 1, 2, … n www. mathssupport. org

The fundamental theorem of algebra. Factorize the polynomial f(x) = x 4 – 6 x 3 + 11 x 2 – 6 x = x (x 3 – 6 x 2 + 11 x – 6) Apply Horner’s algorithm for x = 1 since the sum of the coefficients is equal to zero 1 1 – 6 1 1 5 11 – 6 5 6 6 0 = x (x – 1) (x 2 – 5 x + 6) Apply FTA to factorise the polynomial = x (x – 1) (x – 2) (x – 3) www. mathssupport. org

The fundamental theorem of algebra. Given that 2 is a zero of the polynomial f(x) = x 5 – 4 x 4 – 3 x 3 + 34 x 2 – 52 x + 24 And has a multiplicity of 3, factorize f(x) fully Successively apply Horner’s algorithm with respect to the multiplicity of the given zero 1 2 2 1 2 Apply the FTA to factorise the polynomial Factorize the quadratic expression www. mathssupport. org – 2 2 2 1 2 – 4 0 2 – 3 34 – 52 24 4 14 40 24 – 7 20 12 0 – 12 7 0 14 – 7 6 7 12 0 6 3 0 4 2 1 f(x) = (x – 2)3(x 2 + 2 x – 3) f(x) = (x – 2)3 (x – 1) (x + 3)

Conjugate root theorem www. mathssupport. org

Conjugate root theorem. Given a polynomial f(x) = anxn + an-1 xn-1 + an-2 xn-2 + … + a 2 x 2 + a 1 x + a 0 ak ℝ, k = 0, 1, 2, … n, and an ≠ 0 that has a complex zero z, then its conjugate z* is also a zero of the polynomial f. f(z) = anzn + an-1 zn-1 + … + a 2 z 2 + a 1 z + a 0 = 0 If z is a zero We have to prove that its conjugate z* is also a zero f(z*) = an(z*)n+an-1(z*)n-1+…+a 2(z*)2 +a 1(z*)+a 0 = 0 Using the properties of conjugate numbers: Conjugate of a *) = a (zn)* +a (z n-1)*+…+a (z 2)*+a (z)*+a f(z n n-1 2 1 0 power Conjugate of a *) = (a zn)* +(a z n-1)*+…+(a z 2)*+(a z)*+(a )* f(z n n-1 2 1 0 product Conjugate of a *) = (a zn +a z n-1+…+a z 2 +a z+a )* * f(z = (f(z)) n n-1 2 1 0 sum f(z*) = (f(z))* = 0 QED www. mathssupport. org
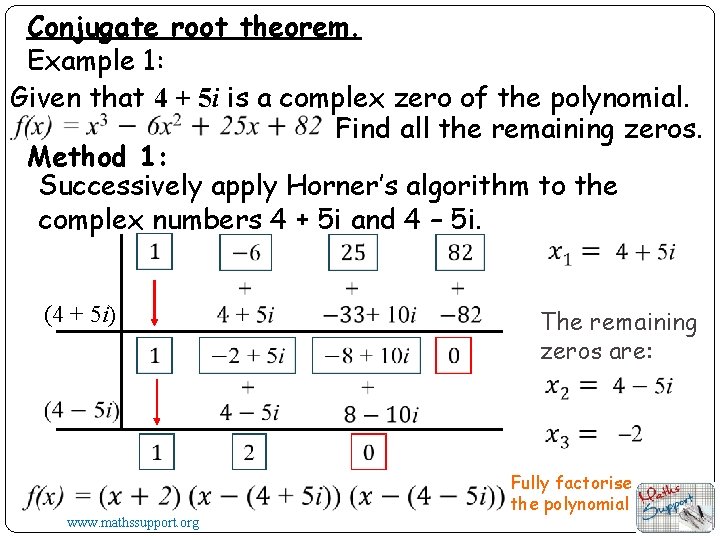
Conjugate root theorem. Example 1: Given that 4 + 5 i is a complex zero of the polynomial. Find all the remaining zeros. Method 1: Successively apply Horner’s algorithm to the complex numbers 4 + 5 i and 4 – 5 i. (4 + 5 i) www. mathssupport. org The remaining zeros are: Fully factorise the polynomial

Conjugate root theorem. Example 1: Given that 4 + 5 i is a complex zero of the polynomial. Find all the remaining zeros. Method 2: Use the conjugate root theorem: The first two factors are: Expanding brackets Using long division to find the last linear factor x +2 x 3 – 6 x 2 + 25 x + 82 – (x 3 – 8 x + 41 x ) 2 x 2 – 16 x + 82 – (2 x 2 – 16 x + 82 ) 0 www. mathssupport. org The remaining zeros are: Fully factorised polynomial

Sum and product of polynomial roots www. mathssupport. org

Polynomials of third degree. Given a cubic equation ax 3 + bx 2 + cx + d = 0 a, b, c, d ℝ and a ≠ 0 and x 1, x 2 and x 3 are the solutions We can factorise the cubic polynomial f(x) = ax 3 + bx 2 + cx + d = a(x – x 1) (x – x 2) (x – x 3) Dividing by a [(x – x 1) (x – x 2)](x – x 3) Expanding the right hand side of the equation Expanding the first two brackets [x 2 – x 2 x – x 1 x + x 1 x 2] (x – x 3) Multiplying out the third bracket x 3 – x 2 x 2 – x 1 x 2 + x 1 x 2 x – x 3 x 2 + x 2 x 3 x + x 1 x 3 x – x 1 x 2 x 3) Put the terms in order x 3 – x 1 x 2 – x 2 x 2 – x 3 x 2 + x 1 x 2 x + x 1 x 3 x + x 2 x 3 x – x 1 x 2 x 3 Grouping x 3 – (x 1 + x 2 + x 3)x 2 + (x 1 x 2 + x 1 x 3 + x 2 x 3)x – x 1 x 2 x 3 [ www. mathssupport. org ] [ ]

Polynomials of third grade. x 3– (x 1+x 2+x 3)x 2 + (x 1 x 2+x 1 x 3+x 2 x 3)x – x 1 x 2 x 3 – (x 1+x 2+x 3) (x 1 x 2+x 1 x 3+x 2 x 3) – (x 1 x 2 x 3) These are Viète’s formulae for cubic equations. Find a similar formulae that satisfy the relationship between the zeros and the coefficients of a quartic polynomial. ax 4 + bx 3 + cx 2 + dx + e = 0 a, b, c, d, e ℝ and a ≠ 0 www. mathssupport. org

Polynomials of the nth degree. Given a polynomial f(x) = anxn + an-1 xn-1 + an-2 xn-2 + … + a 2 x 2 + a 1 x + a 0 With real or complex coefficients (an ≠ 0 ) and zeros x 1, x 2 … xn then x 1+x 2+x 3+ … +xn (x 1 x 2+x 1 x 3+ … +x 1 xn+ x 2 x 3+ x 2 x 4+ … +x 2 xn+ … xn-1 xn. . x 1 x 2 x 3… xn. www. mathssupport. org

Polynomials of the nth degree. Example 1: Find the sum and product of the zeros of these polynomial. For a polynomial of degree n you need to use: an, an-1 and a 0 n=4 an = a 4 = 1 x 1+x 2+x 3+x 4 x 1 x 2 x 3 x 4 www. mathssupport. org

Polynomials of the nth degree. Example 2: Find the sum and product of the zeros of these polynomial. For a polynomial of degree n you need to use: an, an-1 and a 0 n=5 an = a 5 = 3 x 1+x 2+x 3+x 4+x 5 x 1 x 2 x 3 x 4 x 5 www. mathssupport. org

Polynomials of the nth degree. Example 3: Find a quadratic whose roots are Let the desired quadratic be x 2 + bx + c, where we wish to find b and c. Then Viete's formula tells us n=2 an = a 2 = 1 x 1+x 2 = 3 + 2 i + x 1 = 3 + 2 i x 1 x 2 = (3 + 2 i) So the desired quadratic is www. mathssupport. org

Polynomials of the nth degree. Example 4: If the sum of the reciprocals of the roots of the quadratic What is k? x 1 and x 2 are the roots x 1+x 2 x 1 x 2 www. mathssupport. org

Thank you for using resources from For more resources visit our website https: //www. mathssupport. org If you have a special request, drop us an email info@mathssupport. org www. mathssupport. org
- Slides: 17