13 5 The Law of Sines Objectives Use

13 -5 The Law of Sines Objectives Use trig. to find the area of triangles. Use the Law of Sines to find the side lengths and angle measures of a triangle. Holt Algebra 2

13 -5 The Law of Sines Notes #1 -3 1. Find the area of the triangle. Round to the nearest tenth. 2. Solve the triangle. 3. Triangular banners can be formed using the measurements a = 48, b = 28, and m A = 35°. Solve the triangle (nearest tenth). Holt Algebra 2

13 -5 The Law of Sines Example 1: Determining the Area of a Triangle Find the area of the triangle. Round to the nearest tenth. Area = ab sin C Write the area formula. Substitute 3 for a, 5 for b, and 40° for C. ≈ 4. 82 Holt Algebra 2 Use a calculator to evaluate the expression (round).

13 -5 The Law of Sines The area of ∆ABC is equal to bc sin A or ac sin B or ab sin C. By setting these expressions equal to each other, you can derive the Law of Sines. bc sin A = ac sin B = ab sin C bc sin A ac sin B ab sin C = = abc abc sin A = sin B = sin C b c a Holt Algebra 2 Multiply each expression by 2. Divide each expression by abc. Divide out common factors.

13 -5 The Law of Sines Holt Algebra 2

13 -5 The Law of Sines Example 2 A: Using the Law of Sines for AAS and ASA Solve the triangle. Round to the nearest tenth. Step 1. Find the third angle measure. 33° + m E + 28° = 180° m E = 119° Holt Algebra 2 Substitute 33° for m D and 28° for m F. Solve for m E.

13 -5 The Law of Sines Example 2 A Continued Step 2 Find the unknown side lengths. sin F sin D = d f sin 33° sin 28° = d 15 Law of Sines. Substitute. sin F sin E e = f sin e 119° sin 28° = 15 Cross e sin 28° = 15 sin d sin 28° = 15 sin 33° multiply. 119° 15 sin 33° e = d= sin 28° Solve for the d ≈ 17. 4 e ≈ 27. 9 unknown side. Holt Algebra 2

13 -5 The Law of Sines Example 2 B: Using the Law of Sines for AAS and ASA Solve the triangle. Round to the nearest tenth. Step 1 Find the third angle measure. r Q m P = 180° – 36° – 39° = 105° Holt Algebra 2 Triangle Sum Theorem

13 -5 The Law of Sines Example 2 B: Using the Law of Sines for AAS and ASA Solve the triangle. Round to the nearest tenth. Step 2 Find the unknown side lengths. sin P = sin Q p q Law of Sines. r Q sin P = sin R p r sin 105°= sin 39° sin 105°= sin 36° Substitute. r q 10 10 10 sin 36° 10 sin 39° q= r= ≈ 6. 1 ≈ 6. 5 sin 105° Holt Algebra 2

13 -5 The Law of Sines Example 3: Art Application Triangular banners can be formed using the measurements a = 50, b = 20, and m A = 28°. Solve the triangle (nearest tenth). Step 1 Determine m B. m Holt Algebra 2 B = Sin-1

13 -5 The Law of Sines Example 3 Continued Step 3 Find the other unknowns in the triangle. 28° + 10. 8° + m C = 180° m C = 141. 2° Solve for c. c ≈ 66. 8 Holt Algebra 2
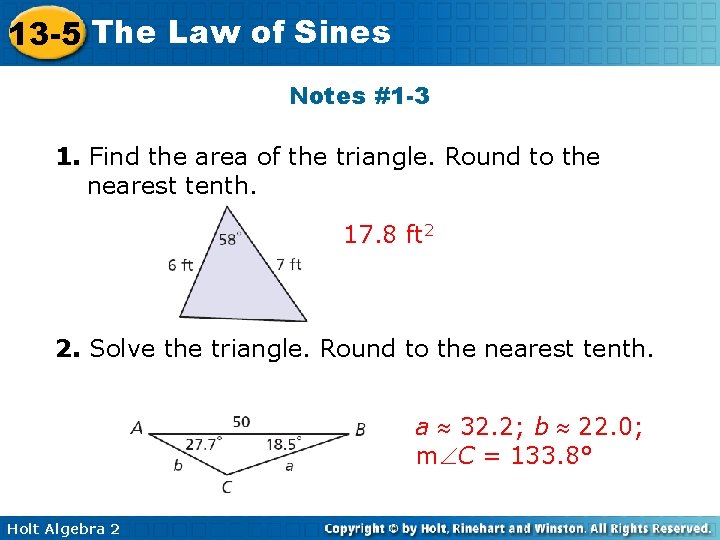
13 -5 The Law of Sines Notes #1 -3 1. Find the area of the triangle. Round to the nearest tenth. 17. 8 ft 2 2. Solve the triangle. Round to the nearest tenth. a 32. 2; b 22. 0; m C = 133. 8° Holt Algebra 2

13 -5 The Law of Sines Example 3: Art Application Triangular banners can be formed using the measurements a = 48, b = 28, and m A = 35°. Solve the triangle (nearest tenth). Holt Algebra 2

13 -5 The Law of Sines Notes #3 3. Determine the number of triangular quilt pieces that can be formed by using the measurements a = 14 cm, b = 20 cm, and m A = 39°. Solve each triangle. Round to the nearest tenth. 2; c 1 21. 7 cm; m B 1 ≈ 64. 0°; m C 1 ≈ 77. 0°; c 2 ≈ 9. 4 cm; m B 2 ≈ 116. 0°; m C 2 ≈ 25. 0° Holt Algebra 2
13 -5 The Law of Sines Holt Algebra 2

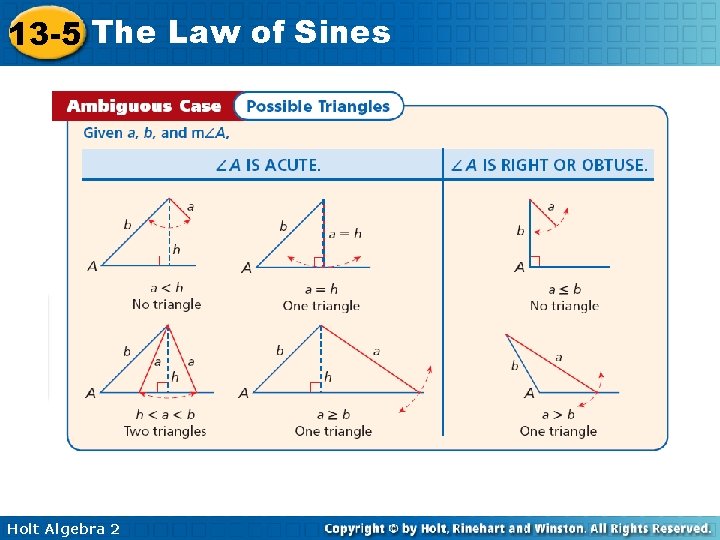
13 -5 The Law of Sines Solving a Triangle Given a, b, and m A Holt Algebra 2
- Slides: 16