13 4 Sterlings Series Derivation from EulerMaclaurin Integration

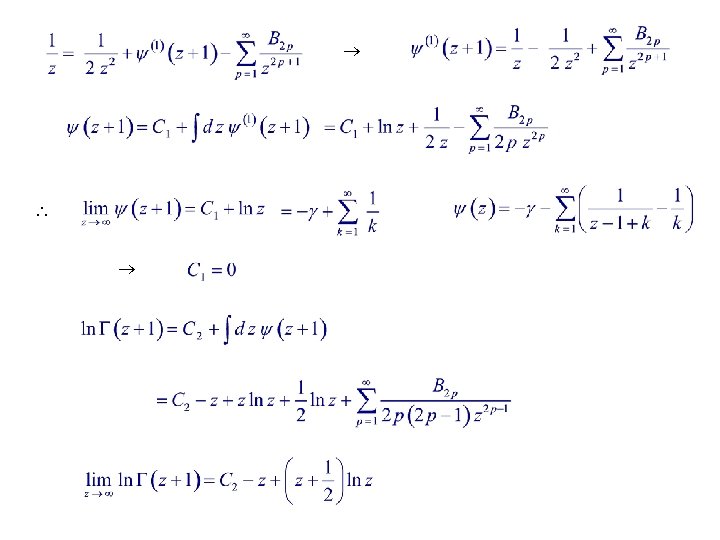
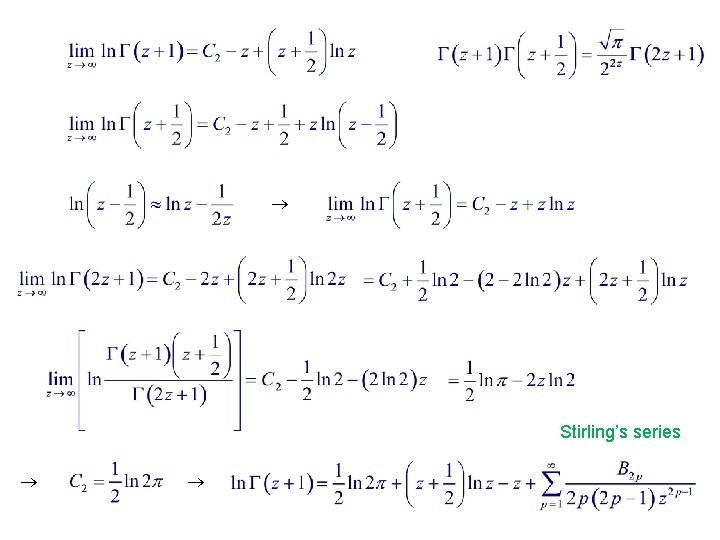


















- Slides: 25

13. 4. Sterling’s Series Derivation from Euler-Maclaurin Integration Formula Euler-Maclaurin integration formula : Let B 2 B 4 B 6 B 8 1/6 1/30 1/42 1/30
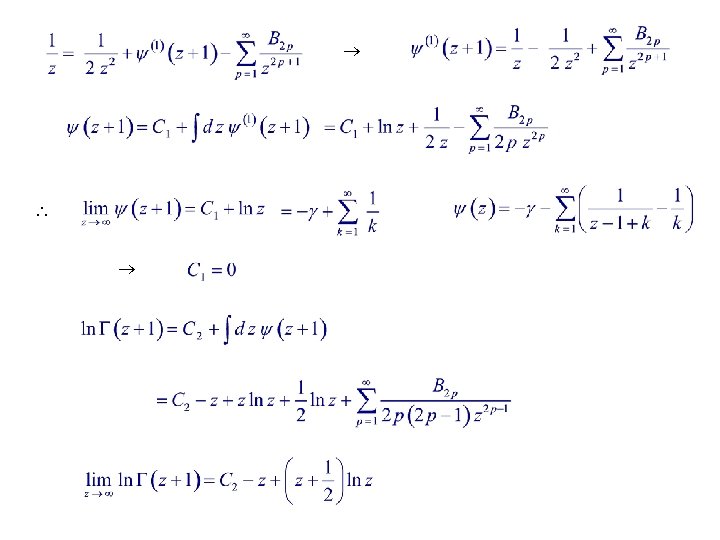
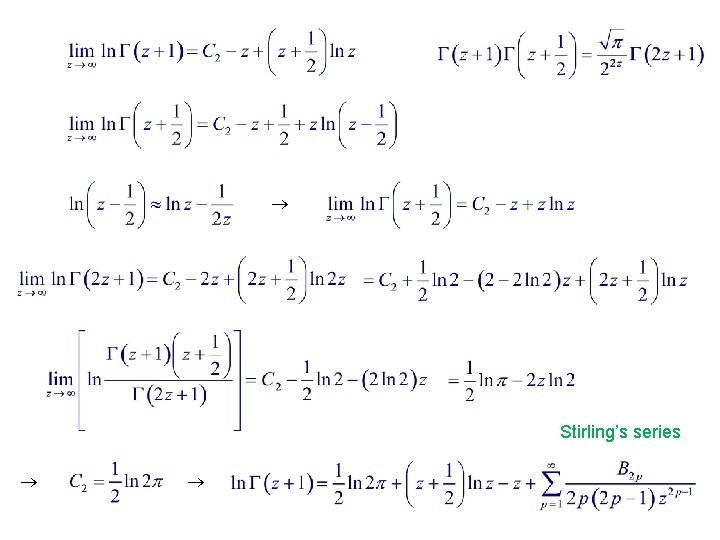
Stirling’s series

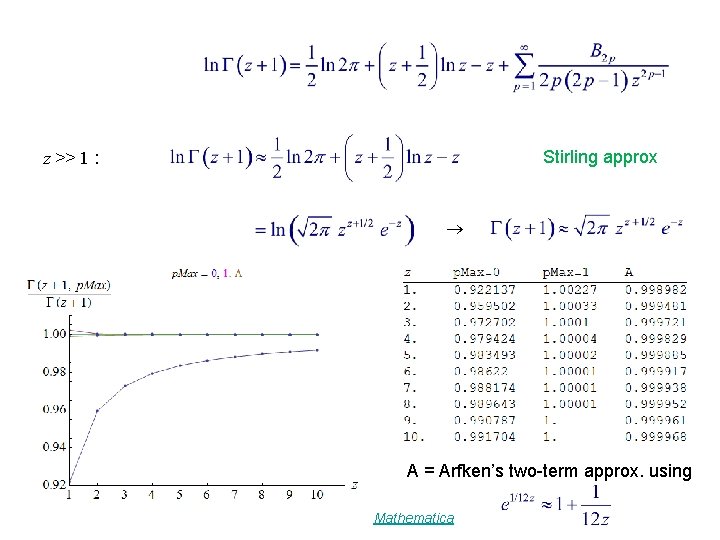
Stirling approx z >> 1 : A = Arfken’s two-term approx. using Mathematica

13. 5. Riemann Zeta Function : Mathematica Integral representation : Proof :

Definition : Contour Integral C 1 0 for Re z >1 diverges for Re z <1 agrees with integral representation for Re z > 1

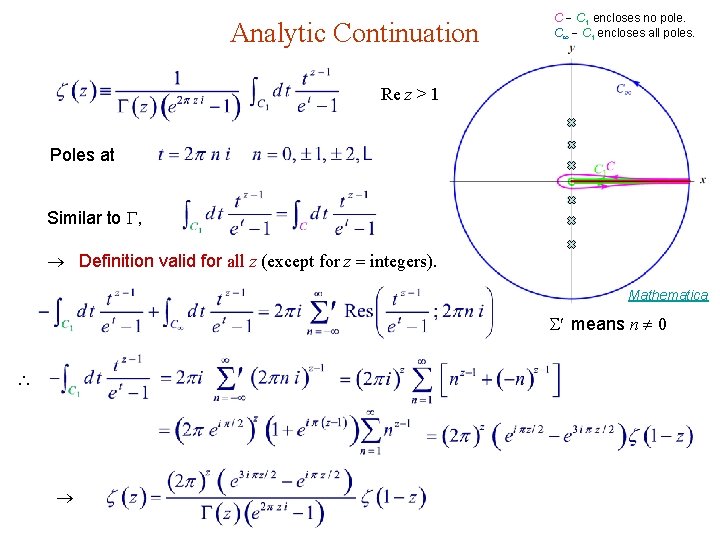
Analytic Continuation C C 1 encloses no pole. C C 1 encloses all poles. Re z > 1 Poles at Similar to , Definition valid for all z (except for z integers). Mathematica means n 0

Riemann’s Functional Equation Riemann’s functional equation

Zeta-Function Reflection Formula zeta-function reflection formula

Riemann’s functional equation : converges for Re z > 1 (z) is regular for Re z < 0. (0) diverges (1) diverges while (0) is indeterminate. for Since the integrand in trivial zeros is always positive, or i. e. , non-trivial zeros of (z) must lie in the critical strip (except for the trivial zeros)

Critical Strip Consider the Dirichlet series : Leibniz criterion , i. e. , for series converges if

(0) Simple poles :

Euler Prime Product Formula ( no terms ) Euler prime product formula

Riemann Hypothesis Riemann found a formula that gives the number of primes less than a given number in terms of the non-trivial zeros of (z). Riemann hypothesis : All nontrivial zeros of (z) are on the critical line Re z ½. Millennium Prize problems proposed by the Clay Mathematics Institute. 1. P versus NP 2. The Hodge conjecture 3. The Poincaré conjecture (proved by G. Perelman in 2003) 4. The Riemann hypothesis 5. Yang–Mills existence and mass gap 6. Navier–Stokes existence and smoothness 7. The Birch and Swinnerton-Dyer conjecture

13. 6. Other Related Functions 1. Incomplete Gamma Functions 2. Incomplete Beta Functions 3. Exponential Integral 4. Error Function

Incomplete Gamma Functions Integral representation: Exponential integral

Series Representation for (n, x)

Series Representation for (n, x)

Series Representation for (a, x) & (a, x) For non-integral a : See Ex 1. 3. 3 & Ex. 13. 6. 4 Pochhammer symbol Relation to hypergeometric functions: see § 18. 6.

Incomplete Beta Functions Ex. 13. 6. 5 Relation to hypergeometric functions: see § 18. 5.

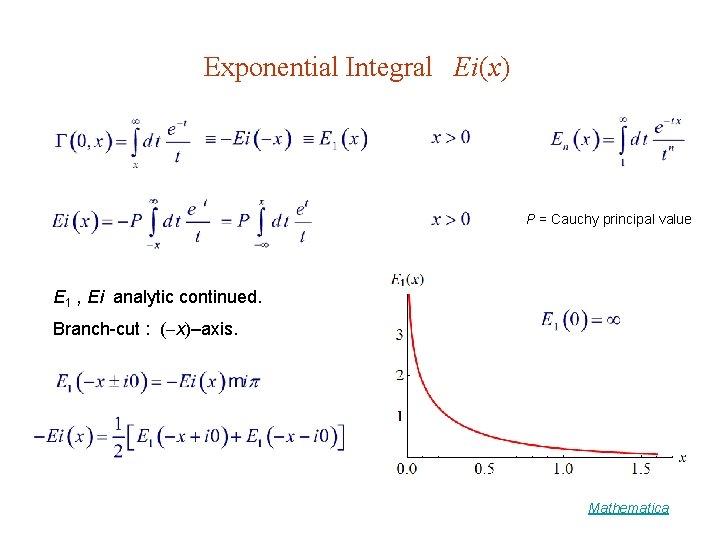
Exponential Integral Ei(x) P = Cauchy principal value E 1 , Ei analytic continued. Branch-cut : ( x)–axis. Mathematica

Series Expansion For x << 1 : For x >> 1 :

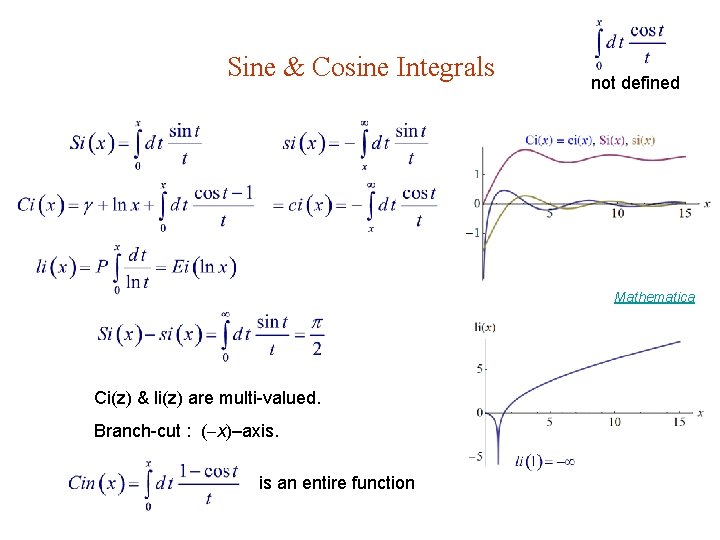
Sine & Cosine Integrals not defined Mathematica Ci(z) & li(z) are multi-valued. Branch-cut : ( x)–axis. is an entire function

Series expansions : Ex. 13. 6. 13. Asymptotic expansions : § 12. 6.

Error Function Power expansion : Asymptotic expansion (see Ex. 12. 6. 3) : Mathematica