13 2 Angles of Rotation Objectives Students will

13 -2 Angles of Rotation Objectives Students will learn how to use special right triangles to find the radian and degrees. Holt Algebra 2

13 -2 Angles of Rotation Vocabulary standard position initial side terminal side angle of rotation coterminal angle reference angle Holt Algebra 2

13 -2 Angles of Rotation A unit circle is a circle with a radius of 1 unit. For every point P(x, y) on the unit circle, the value of r is 1. Therefore, for an angle θ in the standard position: Holt Algebra 2

13 -2 Angles of Rotation So the coordinates of P can be written as (x, y) (cosθ, sinθ). The diagram shows the equivalent degree and radian measure of special angles, as well as the corresponding xand y-coordinates of points on the unit circle. Holt Algebra 2

13 -2 Angles of Rotation Example 2 A: Using the Unit Circle to Evaluate Trigonometric Functions Use the unit circle to find the exact value of each trigonometric function. cos 225° The angle passes through the point on the unit circle. cos 225° = x Holt Algebra 2 Use cos θ = x.

13 -2 Angles of Rotation Example 2 B: Using the Unit Circle to Evaluate Trigonometric Functions Use the unit circle to find the exact value of each trigonometric function. tan The angle passes through the point on the unit circle. Use tan θ = Holt Algebra 2 .

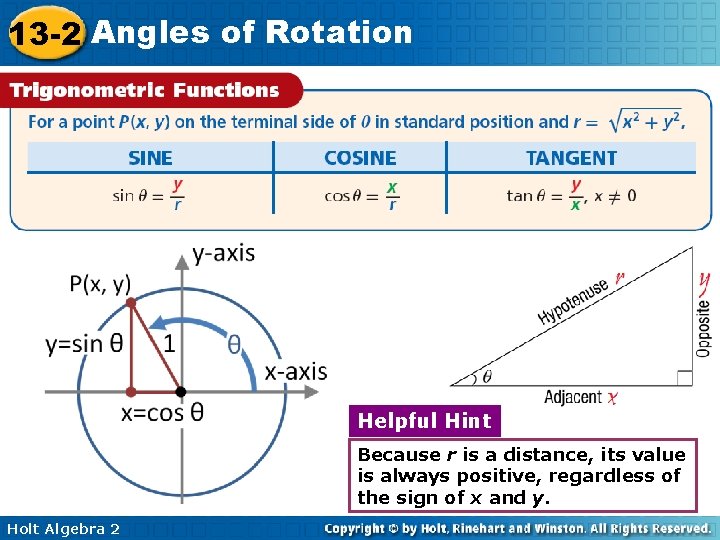
13 -2 Angles of Rotation Helpful Hint Because r is a distance, its value is always positive, regardless of the sign of x and y. Holt Algebra 2

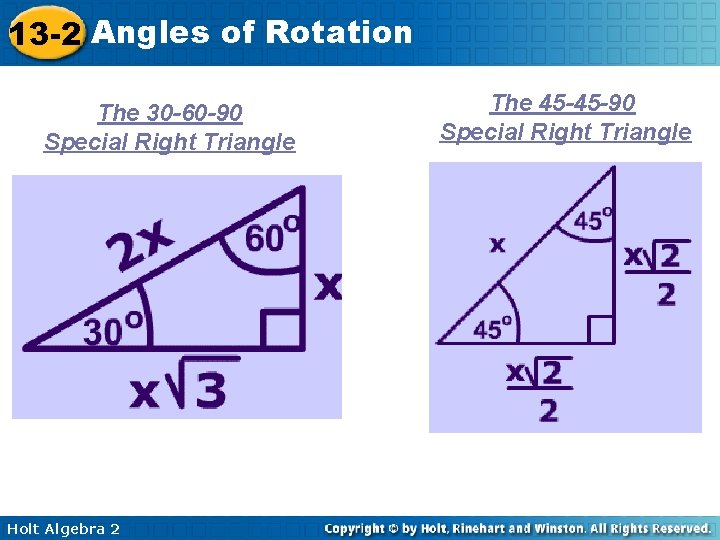
13 -2 Angles of Rotation The 30 -60 -90 Special Right Triangle Holt Algebra 2 The 45 -45 -90 Special Right Triangle

13 -2 Angles of Rotation Trigonometric Functions and Reference Angles Holt Algebra 2

13 -2 Angles of Rotation The diagram shows how the signs of the trigonometric functions depend on the quadrant containing the terminal side of θ in standard position. Holt Algebra 2

13 -2 Angles of Rotation Example 3: Using Reference Angles to Evaluate Trigonometric functions Use a reference angle to find the exact value of the sine, cosine, and tangent of 330°. Step 1 Find the measure of the reference angle. The reference angle measures 360 -330 = 30° Holt Algebra 2

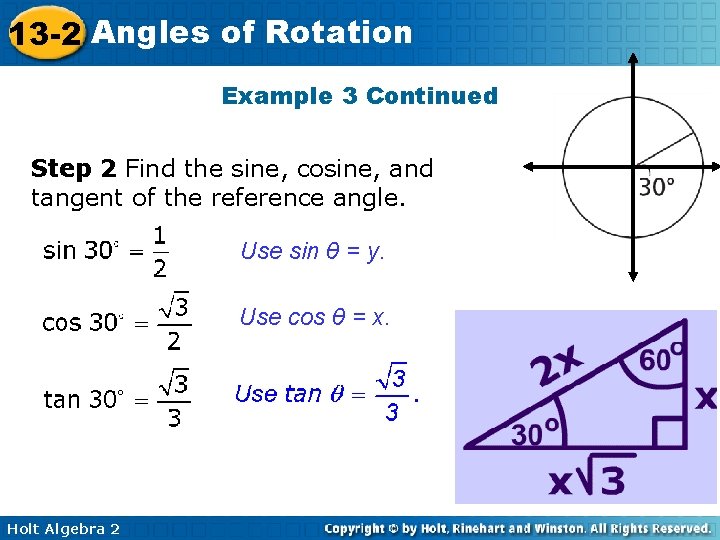
13 -2 Angles of Rotation Example 3 Continued Step 2 Find the sine, cosine, and tangent of the reference angle. Use sin θ = y. Use cos θ = x. Holt Algebra 2

13 -2 Angles of Rotation Example 3 Continued Step 3 Adjust the signs, if needed. In Quadrant IV, sin θ is negative. In Quadrant IV, cos θ is positive. In Quadrant IV, tan θ is negative. Holt Algebra 2

13 -2 Angles of Rotation Evaluate the trigonometric function without using a calculator. Angles are given in degrees. cos 135° Find the reference angle for Quadrant II. Use the sides of a 45°-45°− 90° triangle, then apply the sign of cosine in Quadrant II. Holt Algebra 2

13 -2 Angles of Rotation Evaluate the trigonometric function without using a calculator. Angles are given in degrees. cos 150° Find the reference angle for Quadrant II. Use the sides of a 30°− 60°− 90° triangle, then apply the sign of cosine in Quadrant II. Holt Algebra 2

13 -2 Angles of Rotation Evaluate the trigonometric function without using a calculator. Angles are given in degrees. tan(− 60°) Find the reference angle for Quadrant IV. Use the sides of a 30°− 60°− 90° triangle, then apply the sign of cosine in Quadrant IV. Holt Algebra 2