121117 THE KINEMATIC EQUATIONS FOR PROJECTILE MOTION Objective

12/11/17 THE KINEMATIC EQUATIONS FOR PROJECTILE MOTION Objective: I will identify and apply the equations needed to calculate the range, time of flight, and maximum height of a projectile. PAGE 29

Four Kinematic Equations 1) Δx = ½(vi + vf) t 2) vf = vi + a t 3) Δx = vi t + ½ a t 2 4) vf 2 = vi 2 + 2 a Δx • Can be used for both linear and two-dimensional motion • Acceleration must be constant to use the equations

Four Kinematic Equations

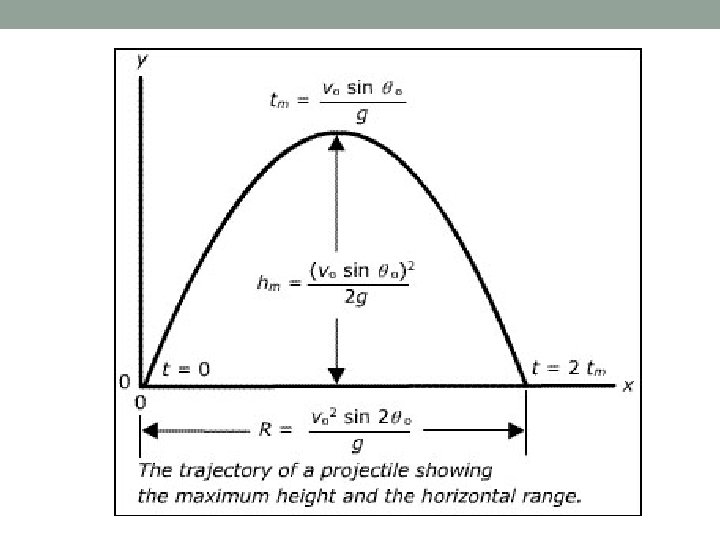
Kinematic Equations for Projectile Motion • By applying our conceptual understanding of projectile motion to make certain assumptions, we can rearrange the kinematic equations to find the following: 1. Time of flight 2. Range 3. Maximum height reached

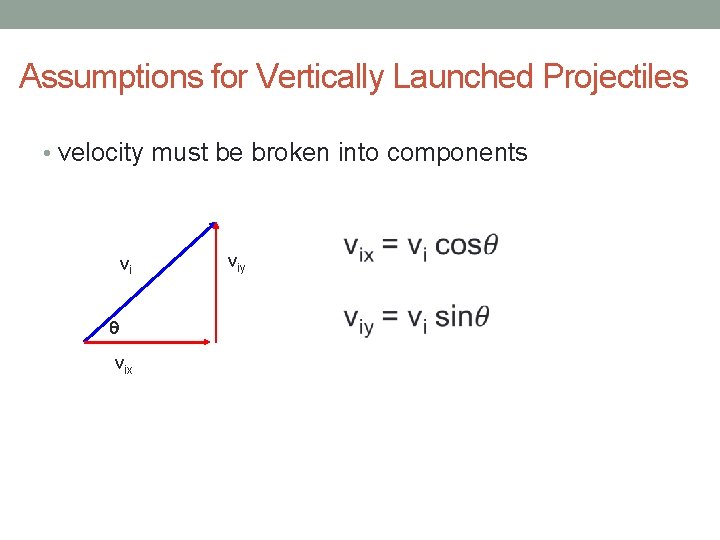
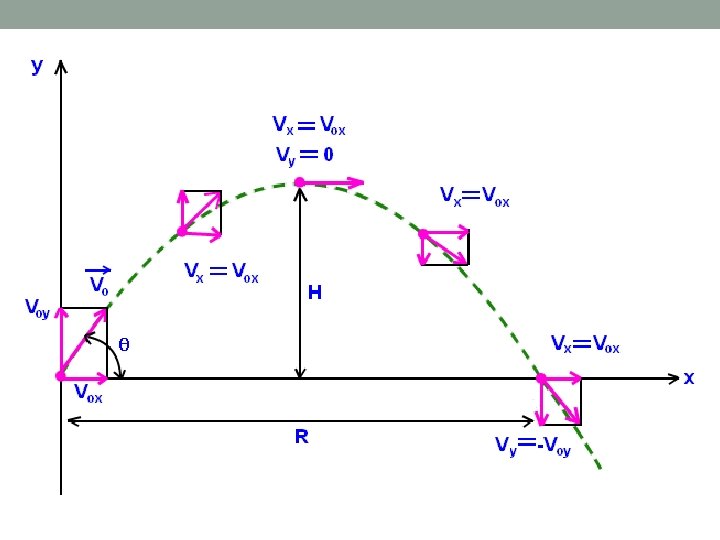
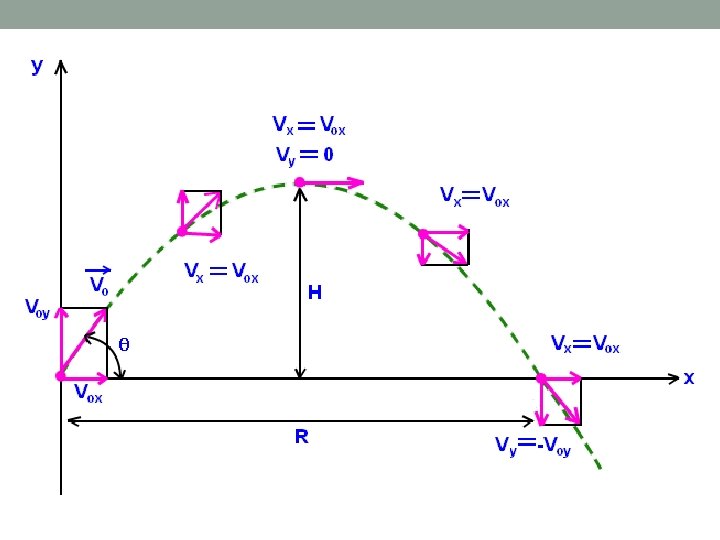
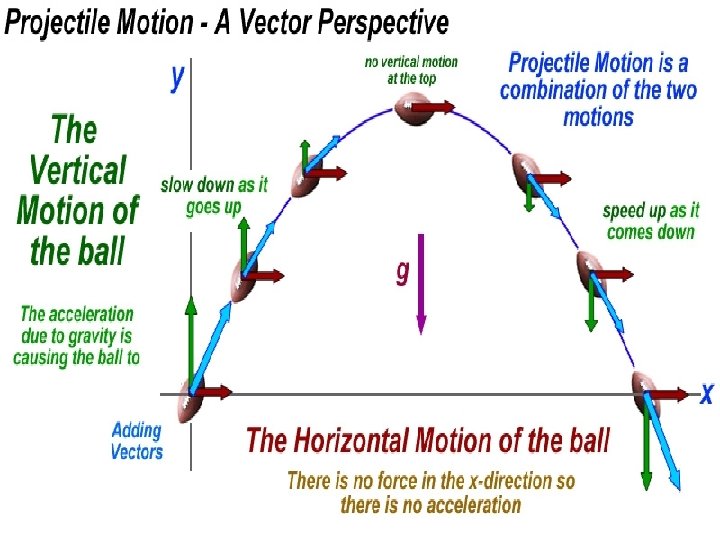
Assumptions for Vertically Launched Projectiles • velocity must be broken into components vi q vix viy

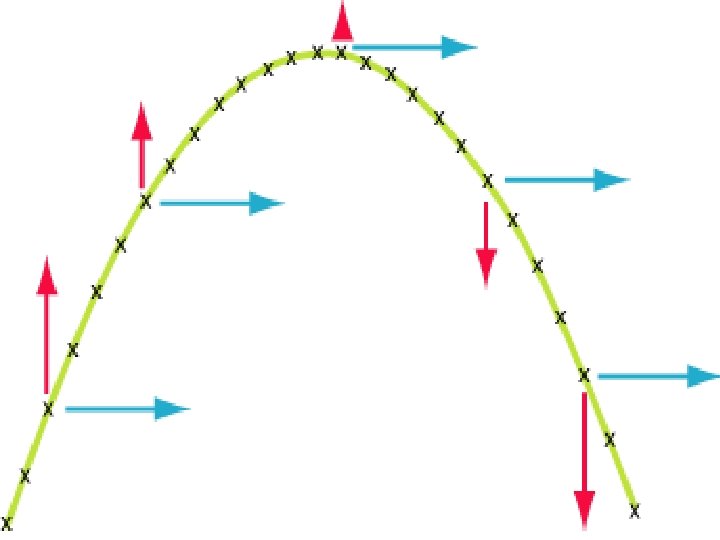
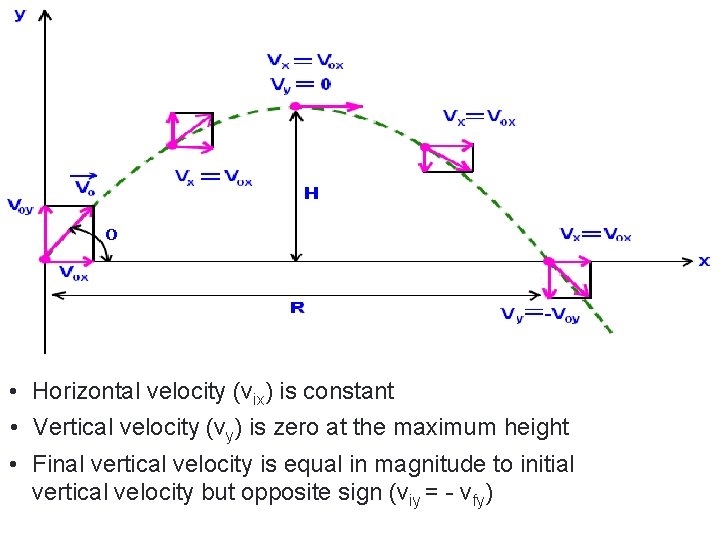
• Horizontal velocity (vix) is constant • Vertical velocity (vy) is zero at the maximum height • Final vertical velocity is equal in magnitude to initial vertical velocity but opposite sign (viy = - vfy)

Time of Flight • Derived from Δy = vi t + ½ g t 2 • when the projectile is launched from and lands at the same height Δy = 0

Range •

Range • When time is unknown: • Derived from vf = vi + a t and Δx = v * t

Maximum Height • When time is known: Δy = ½ g t 2 (using half of entire time) • Parabolic motion is symmetrical so the maximum height will be achieved at half of the total time of flight

Maximum Height • When time is unknown: • Derived from vf 2 = vi 2 + 2 a Δy

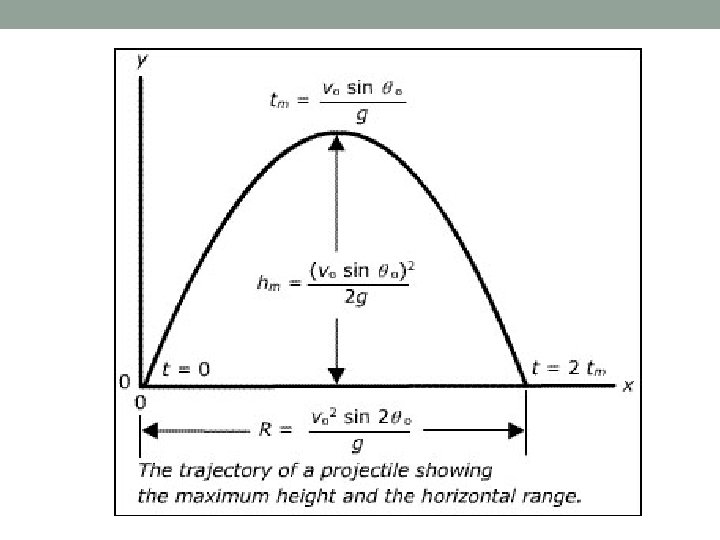
Time of Flight, Range, and Max Height or or

Output Activity (page 28) • Create your own Angry Birds level, military artillery example, or baseball home run example to show your mathematical understanding of projectile motion.

Output Activity (page 28) • Your example must include the following: • An initial velocity and launch angle that make sense for your example • Vectors for initial velocity, horizontal component, and vertical component • Calculated values for vix and viy (show your work) • Calculated values for Range, Time of Flight, and Maximum Height • Assume that the projectile launches and lands at the same height • Work must be shown on the page • The parabolic trajectory is drawn to scale • Launch angle measured using a protractor • Vectors all drawn to scale • Range and Max Height are to scale • The illustration is neat, colorful, detailed, and accurate • Done on graph paper first, then turned in, then taped/glued onto page 28.