12 Iteration und Rekursion Funktionen sind Unterprogramme die

12. Iteration und Rekursion Funktionen sind Unterprogramme, die zur Berechnung eines Wertes dienen, die Aufrufstelle der Funktion muß Ausdruck sein. – Wert der Funktion wird unmittelbar an Aufrufstelle weiterverwendet – Deklaration enthält Namen, Parameterliste und Ergebnistyp – Anweisungsblock enthält Zuweisung an den Namen der Funktion – Seiteneffekte können über globale Variablen und Referenzparameter bewirkt werden FUNCTION Min(X, Y: REAL): REAL BEGIN IF X < Y THEN Min : = X ELSE Min : = Y END; G. Heyer 1 Digitale Informationsverarbeitung

Geschachtelte Unterprogramme PROGRAM Syrakus; USES Win. Crt; FUNCTION Syrakus. Test (n: INTEGER) : BOOLEAN; FUNCTION Ulam(m: INTEGER): INTEGER BEGIN IF Odd(m) THEN Ulam : = 3*m+1 ELSE Ulam : = m DIV 2 END {Ulam} BEGIN WHILE n > 1 DO n : = Ulam(n); Syrakus. Test : = (n = 1) END {Syrakus. Test}; VAR Test. Zahl : Integer; BEGIN Read(Test. Zahl); IF Syrakus. Test(Test. Zahl) THEN Write. Ln(Test. Zahl, ' hat Test bestanden') END. G. Heyer 2 Digitale Informationsverarbeitung

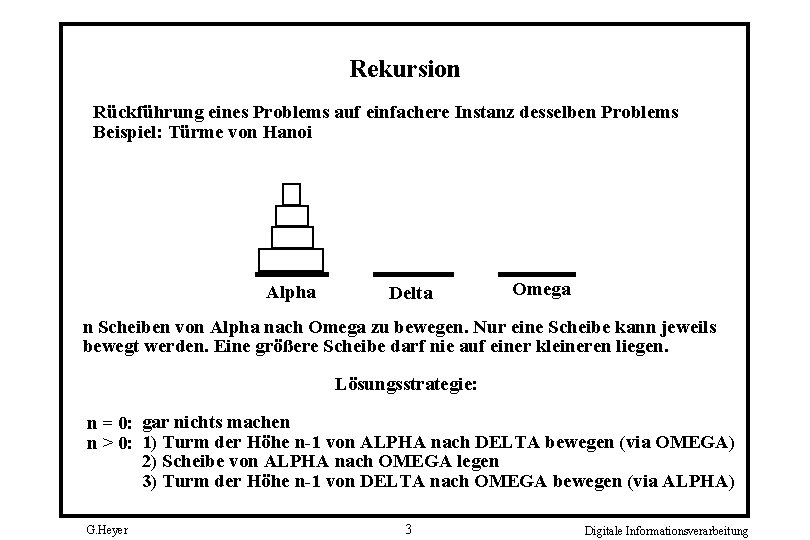
Rekursion Rückführung eines Problems auf einfachere Instanz desselben Problems Beispiel: Türme von Hanoi Alpha Delta Omega n Scheiben von Alpha nach Omega zu bewegen. Nur eine Scheibe kann jeweils bewegt werden. Eine größere Scheibe darf nie auf einer kleineren liegen. Lösungsstrategie: n = 0: gar nichts machen n > 0: 1) Turm der Höhe n-1 von ALPHA nach DELTA bewegen (via OMEGA) 2) Scheibe von ALPHA nach OMEGA legen 3) Turm der Höhe n-1 von DELTA nach OMEGA bewegen (via ALPHA) G. Heyer 3 Digitale Informationsverarbeitung

PROGRAM Hanoi; CONST Gesamthoehe = 4; TYPE Hoehenbereich = [0. . Gesamthoehe]; Platz = (ALPHA, OMEGA, DELTA); PROCEDURE bewege. Turm (Hoehe: Hoehenbereich; von. Platz, nach. Platz, ueber. Platz: Platz); PROCEDURE Drucke. Zug (Start, Ziel: Platz); PROCEDURE Drucke. Platz (spez. Platz: Platz); BEGIN (* Drucke. Platz *) CASE spez. Platz OF ALPHA: Write ('ALPHA'); OMEGA: Write ('OMEGA'); DELTA: Write ('DELTA'); END; (* CASE *) END (* Drucke. Platz *); BEGIN (* Drucke. Zug *) Write('Scheibe ', Hoehe, ' von '); Drucke. Platz (Start); Write(' nach '); Drucke. Platz (Ziel); Write. Ln; END Drucke. Zug; BEGIN (* bewege. Turm *) IF Hoehe > 0 THEN BEGIN bewege. Turm (Hoehe - 1, von. Platz, ueber. Platz, nach. Platz); Drucke. Zug (von. Platz, nach. Platz); bewege. Turm (Hoehe - 1, ueber. Platz, nach. Platz, von. Platz); END (* IF *); END (* bewege. Turm *); BEGIN (* Hanoi *) bewege. Turm (Gesamthoehe, ALPHA, OMEGA, DELTA); END (* Hanoi *). G. Heyer 4 Digitale Informationsverarbeitung

PROGRAM Hanoi; CONST Gesamthoehe = 4; TYPE Hoehenbereich = [0. . Gesamthoehe]; Platz = (ALPHA, OMEGA, DELTA); PROCEDURE bewege. Turm (Hoehe: Hoehenbereich; von. Platz, nach. Platz, ueber. Platz: Platz); PROCEDURE Drucke. Zug (Start, Ziel: Platz); PROCEDURE Drucke. Platz (spez. Platz: Platz); BEGIN (* Drucke. Platz *) CASE spez. Platz OF ALPHA: Write ('ALPHA'); OMEGA: Write ('OMEGA'); DELTA: Write ('DELTA'); END; (* CASE *) END (* Drucke. Platz *); BEGIN (* Drucke. Zug *) Write('Scheibe ', Hoehe, ' von '); Drucke. Platz (Start); Write(' nach '); Drucke. Platz (Ziel); Write. Ln; END Drucke. Zug; BEGIN (* bewege. Turm *) IF Hoehe > 0 THEN BEGIN bewege. Turm (Hoehe - 1, von. Platz, ueber. Platz, nach. Platz); Drucke. Zug (von. Platz, nach. Platz); bewege. Turm (Hoehe - 1, ueber. Platz, nach. Platz, von. Platz); END (* IF *); END (* bewege. Turm *); BEGIN (* Hanoi *) bewege. Turm (Gesamthoehe, ALPHA, OMEGA, DELTA); END (* Hanoi *). G. Heyer 5 Digitale Informationsverarbeitung

Produzierte Ausgabe Scheibe 1 von ALPHA nach DELTA Scheibe 2 von ALPHA nach OMEGA Scheibe 1 von DELTA nach OMEGA Scheibe 3 von ALPHA nach DELTA Scheibe 1 von OMEGA nach ALPHA Scheibe 2 von OMEGA nach DELTA Scheibe 1 von ALPHA nach DELTA Scheibe 4 von ALPHA nach OMEGA Scheibe 1 von DELTA nach OMEGA Scheibe 2 von DELTA nach ALPHA Scheibe 1 von OMEGA nach ALPHA Scheibe 3 von DELTA nach OMEGA Scheibe 1 von ALPHA nach DELTA Scheibe 2 von ALPHA nach OMEGA Scheibe 1 von DELTA nach OMEGA G. Heyer 6 Digitale Informationsverarbeitung

Prinzip der Rekursion Definition komplexer Funktionen durch rekursive Rückführung auf - elementare Ausdrücke für einfache Funktionen - Operationen, die auf Funktionen definiert sind Primitiv rekursive Funktion 1. Null-Funktion (Konstante Funktion) 2. Nachfolger 3. Identität (Projektion) G. Heyer 7 Digitale Informationsverarbeitung

Substitution (Komposition) Primitive Rekursion f: 1 -stellig h: 2 -stellig g: 3 -stellig G. Heyer 8 Digitale Informationsverarbeitung

Fibonacci Funktion Wieviele Kaninchen-Pärchen gibt es nach n Jahren, wenn man im Jahr 1 mit einem Pärchen beginnt, jedes Pärchen vom zweiten Jahr an ein weiteres Pärchen Nachwuchs hat und die Kaninchen nie sterben. Jahr: 1 2 3 4 5 6 7 8. . . Zahl der Pärchen: 1 1 2 3 5 8 13 21. . . Wir definieren: Fibonacci(n) = 1 für n = 1, 2 Fibonacci(n) = Fibonacci(n-1) + Fibonacci(n-2) für n > 2. FUNCTION Fib 1 (Argument: INTEGER) : INTEGER; BEGIN (* Fib 1 *) IF Argument <= 2 THEN Fib 1 : = 1 ELSE Fib 1 : = Fib 1(Argument-1) + Fib 1(Argument-2) END (* Fib 1 *); Exponentielle Anzahl rekursiver Aufrufe: bei G. Heyer 9 Fib 1(30) bereits 1. 664. 079 Aufrufe ! Digitale Informationsverarbeitung

Lösung mit linearer Anzahl von Aufrufen (rekursiv nicht-funktional) FUNCTION Fib 2 (Arg: INTEGER) : INTEGER; PROCEDURE Fib. Proc (Arg: INTEGER; VAR Fib, Fib. Min 1: INTEGER ); (* Liefert fuer Arg >= 0 in Fib die Fibonacci-Zahl *) (* von Arg in Fib. Min 1 die von Arg-1. *) (* Fuer Arg = 0 ist Fib. Min 1 undef. *) VAR Fib. Min 2 : INTEGER; BEGIN (* Fib. Proc *) IF Arg <= 1 THEN BEGIN Fib : = Arg; Fib. Min 1 : = 0 END ELSE BEGIN Fib. Proc (Arg - 1, Fib. Min 2); Fib : = Fib. Min 1 + Fib. Min 2; END (* IF *); END (* Fib. Proc *); VAR Fib. Res 1, Fib. Res 2 : INTEGER; BEGIN (* Fib 2; dient nur zur Anpassung der Schnittstelle *) Fib. Proc (Arg, Fib. Res 1, Fib. Res 2); Fib 2 : = Fib. Res 1 END (* Fib 2 *); G. Heyer 10 Digitale Informationsverarbeitung

Iterative Lösung mit Umspeichern FUNCTION Fib 3 (Arg: INTEGER) : INTEGER; (* Iterative Variante ohne Feld *) VAR Index, Fib. Min 1, Fib. New: INTEGER; BEGIN (* Fib 3 *) IF Arg = 0 THEN Fib 3 : = 0 ELSE BEGIN Fib. Min 1: = 0; Fib: = 1; FOR Index: = 2 TO Arg DO BEGIN Fib. New: = Fib + Fib. Min 1; Fib. Min 1: = Fib; Fib: = Fib. New; END (* FOR *); Fib 3 : = Fib END (* IF *); END (* Fib 3 *); G. Heyer 11 Digitale Informationsverarbeitung

Iterative Lösung ohne Umspeichern PROCEDURE Fib 4 (Arg: INTEGER) : INTEGER; (* Iterative Variante mit Ringpuffer *) VAR Ring 0, Ring 1, Pos : INTEGER; BEGIN (* Fib 4 *) Ring 0: = 0; Ring 1 : = 1; (* Initialisierung des Rings *) FOR Pos : = 2 TO Arg DO (* Berechnung *) IF Pos MOD 2 = 0 THEN Ring 0 : = Ring 0 + Ring 1 ELSE Ring 1 : = Ring 0 + Ring 1; IF Arg MOD 2 = 0 THEN Fib 4 : = Ring 0 ELSE Fib 4 : = Ring 1; END (* Fib 4 *); G. Heyer 12 Digitale Informationsverarbeitung

Indirekte Rekursion kann auch dadurch entstehen, daß ein in Unterprogramm U 1 aufgerufenes Unterprogramm U 2 den Aufruf von U 1 bewirkt FUNCTION Gerade(N : Integer) : Boolean; BEGIN IF N = 0 THEN Gerade : = True ELSE Gerade : = Un. Gerade(n - 1) END; FUNCTION Un. Gerade(N : Integer) : Boolean; BEGIN IF N = 0 THEN Un. Gerade : = False ELSE Un. Gerade : = Gerade(n - 1) END; Jeder Bezeichner muß vor der ersten Benutzung deklariert sein! FUNCTION Un. Gerade(N : Integer) : Boolean; FORWARD; muß vor der Deklaration von Gerade stehen G. Heyer 13 Digitale Informationsverarbeitung

Endrekursion Eine Funktion f heißt endrekursiv, falls sie von folgender Form ist: f(x) = { g(x) f(r(x)) falls P(x) sonst r(x) ist dabei "einfacher" als x. Für Terminierung muß gelten: Für jedes x gibt es ein n, so daß rn (x) P erfüllt. nicht endrekursiv: { (x = 0) x≤ 1 Even 1(x) = Even 1(x - 2) sonst Even 2(x) = { x≤ 1 (x = 0) not Even 2(x - 1) sonst endrekursive Funktionen einfach iterativ zu berechnen: WHILE not P(x) DO x : = r(x); f : = g(x) G. Heyer 14 Digitale Informationsverarbeitung