12 Inequalities and Linear Programming a How to

12. Inequalities and Linear Programming (a) How to solve the quadratic inequalities in one unknown by using graphical method? (i) a > 0, solve ax 2+bx+c > 0. Using the graph of y = ax 2+bx+c, find the range of values of x by reading the points lying above the x-axis. The x-intercepts of the quadratic graph y = ax 2+bx+c are and β. y For y > 0, or x< the solution of the inequality is above the x-axis, i. e. the blue curve. O y = ax 2+bx+c x >β β x

12. Inequalities and Linear Programming (a) How to solve the quadratic inequalities in one unknown by using graphical method? (i) a > 0, solve ax 2+bx+c < 0. Using the graph of y = ax 2+bx+c, find the range of values of x by reading the points lying below the x-axis. The x-intercepts of the quadratic graph y = ax 2+bx+c are and β. y For y < 0, the solution of the inequality is below the x-axis, i. e. the orange curve. O y = ax 2+bx+c β < x <β x

12. Inequalities and Linear Programming (a) How to solve the quadratic inequalities in one unknown by using graphical method? (ii) a < 0, solve ax 2+bx+c > 0. Using the graph of y = ax 2+bx+c, find the range of values of x by reading the points lying above the x-axis. y ∵ The quadratic graph is vertically < x <β inverted compared with (i), ∴ The range of values of x is opposite to the case a > 0. O For y > 0, the solution of the inequality is above the x-axis, i. e. the blue curve. y = ax 2+bx+c β x

12. Inequalities and Linear Programming (a) How to solve the quadratic inequalities in one unknown by using graphical method? (ii) a < 0, solve ax 2+bx+c < 0. Using the graph of y = ax 2+bx+c, find the range of values of x by reading the points lying below the x-axis. y ∵ The quadratic graph is vertically inverted compared with (i), ∴ The range of values of x is opposite to the case a > 0. For y < 0, or O x< β x x >β y = ax 2+bx+c the solution of the inequality is below the x-axis, i. e. the orange curve.

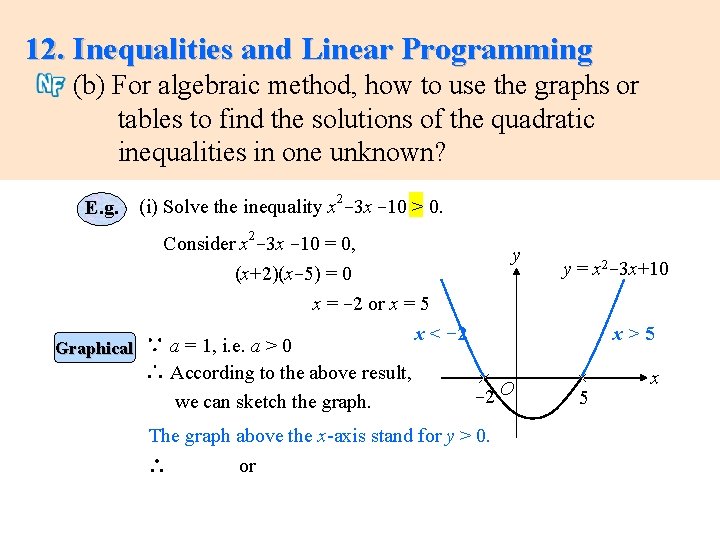
12. Inequalities and Linear Programming (b) For algebraic method, how to use the graphs or tables to find the solutions of the quadratic inequalities in one unknown? 2 E. g. (i) Solve the inequality x -3 x -10 > 0. Consider x 2 -3 x -10 = 0, y (x+2)(x-5) = 0 x = -2 or x = 5 x < -2 ∵ a = 1, i. e. a > 0 Graphical ∴ According to the above result, -2 O we can sketch the graph. The graph above the x-axis stand for y > 0. or ∴ y = x 2 -3 x+10 x>5 5 x

12. Inequalities and Linear Programming (b) For algebraic method, how to use the graphs or tables to find the solutions of the quadratic inequalities in one unknown? 2 E. g. (i) Solve the inequality x -3 x -10 > 0. Consider x 2 -3 x -10 = 0, (x+2)(x-5) = 0 x = -2 or x = 5 Tabular x < -2 -2 < x < 5 + x+2 x-5 (x+2)(x-5) + ∴ x < -2 or x > 5 x>5 + + + -2<x<5 x>5 x<-2 x>5 -2+2<x+2<5+2 -2 -5<x-5<5 -5 x+2>5+2 x+2<0 x+2>0 x-5<-2 -5 x+2<-2+2 (x+2)(x-5)>0 (x+2)(x-5)<0 x-5>5 -5 -7<x-5<0 0<x+2<7 x+2>7 x-5<0 x-5>0 x+2<0 x-5>0 x-5<0 x+2>0

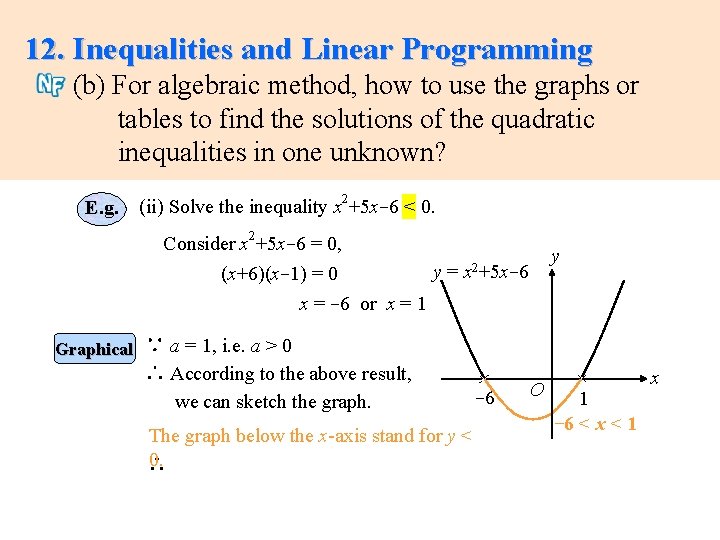
12. Inequalities and Linear Programming (b) For algebraic method, how to use the graphs or tables to find the solutions of the quadratic inequalities in one unknown? 2 E. g. (ii) Solve the inequality x +5 x-6 < 0. Consider x 2+5 x-6 = 0, y= (x+6)(x-1) = 0 x = -6 or x = 1 y x 2+5 x-6 Graphical ∵ a = 1, i. e. a > 0 ∴ According to the above result, we can sketch the graph. The graph below the x-axis stand for y < 0. ∴ -6 O 1 -6 < x < 1 x

12. Inequalities and Linear Programming (b) For algebraic method, how to use the graphs or tables to find the solutions of the quadratic inequalities in one unknown? 2 E. g. (ii) Solve the inequality x +5 x-6 < 0. Consider x 2+5 x-6 = 0, (x+6)(x-1) = 0 x = -6 or x = 1 Tabular x < -6 x+6 x-1 (x+6)(x-1) + ∴ -6 < x < 1 + - x>1 + + + x<-1 x>1 -6<x<1 x<-6 x>1 x-1<-6 -1 x+6>1+6 x+6<0 x+6>0 -6+6<x+6<1+6 -6 -1<x-1<1 -1 x+6<-6+6 (x+6)(x-1)<0 (x+6)(x-1)>0 x-1>1 -1 x+6>7 x-1<0 x-1<-7 x-1>0 -7<x-1<0 0<x+6<7 x+6<0 x-1>0 x-1<0 x+6>0

12. Inequalities and Linear Programming Solving Quadratic Inequalities Easy Memory Tips： ax 2+bx+c > 0 When the quadratic function and a (the coefficient of x 2) are both larger than zero or smaller than zero, ax 2+bx+c < 0 the solution of the inequality is x < or x >β. Otherwise, the solution of the inequality is < x <β. a>0 a<0 ax 2+bx+c > 0 a<0 ax 2+bx+c < 0 a>0