12 HashTable Data Structures Hashtable principles Closedbucket and

12 Hash-Table Data Structures • Hash-table principles. • Closed-bucket and open-bucket hash tables. • Searching, insertion, deletion. • Hash-table design. • Implementations of sets and maps using hash tables. © 2001, D. A. Watt and D. F. Brown

Hash-table principles (1) • If a map’s keys are small integers, we can represent the map by a key-indexed array. Search, insertion, and deletion then have time complexity O(1). • Can we approach this performance with keys of other types? Yes! • Hashing: translate each key to a small integer, and use that integer to index an array. • A hash table is an array of m buckets, together with a hash function hash(k) that translates each key k to a bucket index (in the range 0…m– 1).

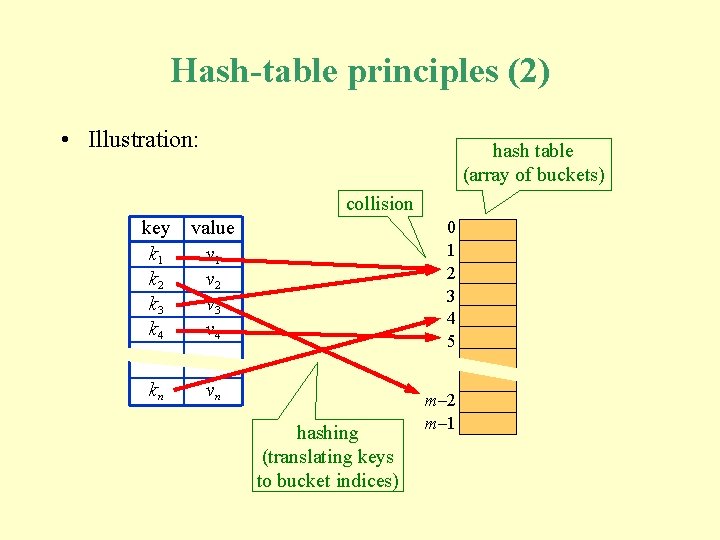
Hash-table principles (2) • Illustration: hash table (array of buckets) collision key k 1 k 2 k 3 k 4 value v 1 v 2 v 3 v 4 kn vn 0 1 2 3 4 5 hashing (translating keys to bucket indices) m– 2 m– 1

Hash-table principles (3) • Each key k has a home bucket in the hash table, namely the bucket with index hash(k). • To insert a new entry with key k into the hash table, assign that entry to k’s home bucket. • To search for an entry with key k in the hash table, look in k’s home bucket. • To delete an entry with key k from the hash table, look in k’s home bucket.

Hash-table principles (4) • The hash function must be consistent: k 1 = k 2 implies hash(k 1) = hash(k 2). • In general, the hash function is many-to-one. • Therefore different keys may share the same home bucket: k 1 k 2 but hash(k 1) = hash(k 2). This is called a collision. • Always prefer a hash function that makes collisions relatively infrequent.

Example 1: a hash function for words • Suppose that the keys are English words. • Possible hash function: m = 26 hash(w) = (initial letter of w) – ‘A’ • All words with initial letter ‘A’ share bucket 0; … all words with initial letter ‘Z’ share bucket 25. • This is a convenient choice for illustrative purposes. • This is a poor choice for practical purposes: collisions are likely to be frequent in some buckets.

Hashing in Java (1) • Instance method in class Object: public int hash. Code (); // Translate this object to an integer, such that x. equals(y) // implies x. hashcode() == y. hashcode(). • Note that hash. Code is consistent. We can use it to implement a hash function for a hash table with m buckets: int hash (Object k) { return Math. abs(k. hash. Code()) % m; } Math. abs returns a Modulo-m arithmetic then gives nonnegative integer. an integer in the range 0…m– 1.

Hashing in Java (2) • Each subclass of Object should override hash. Code. • Examples: Class of k String Result of k. hash. Code() weighted sum of characters of k Integer integer value of k Date (high 32 bits of k) exclusive-or (low 32 bits of k), where k is expressed in milliseconds since 1970 -01 -01

Closed- vs open-bucket hash tables • Closed-bucket hash table: § Each bucket may be occupied by several entries. § Buckets are completely separate. • Open-bucket hash table: § Each bucket may be occupied by at most one entry. § Whenever there is a collision, displace the new entry to another bucket.

Closed-bucket hash tables (1) • Closed-bucket hash table (CBHT): § Each bucket may be occupied by several entries. § Buckets are completely separate. • Simplest implementation: each bucket is an SLL. • In the following illustrations, keys are names of chemical elements. Assume: m = 26 hash(e)= (initial letter of e) – ‘A’

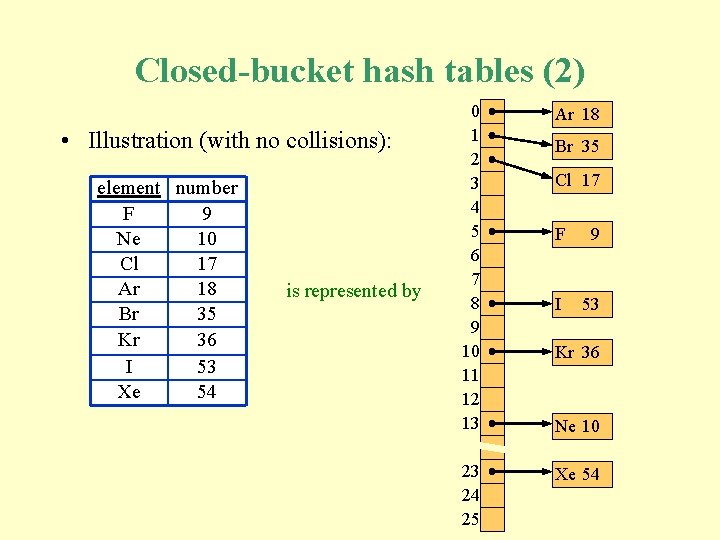
Closed-bucket hash tables (2) • Illustration (with no collisions): element number F 9 Ne 10 Cl 17 Ar 18 Br 35 Kr 36 I 53 Xe 54 is represented by 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Ar 18 23 24 25 Xe 54 Br 35 Cl 17 F 9 I 53 Kr 36 Ne 10

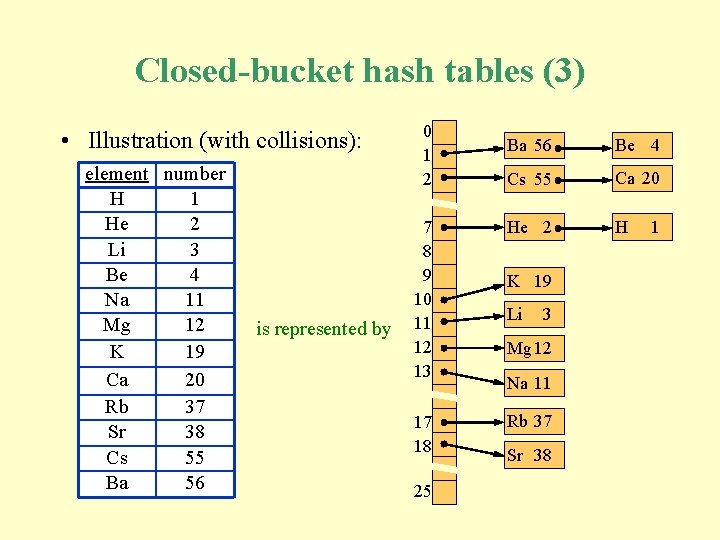
Closed-bucket hash tables (3) • Illustration (with collisions): element number H 1 He 2 Li 3 Be 4 Na 11 Mg 12 K 19 Ca 20 Rb 37 Sr 38 Cs 55 Ba 56 is represented by 0 1 2 Ba 56 Be 4 Cs 55 Ca 20 7 8 9 10 11 12 13 He 2 H 17 18 Rb 37 25 K 19 Li 3 Mg 12 Na 11 Sr 38 1

Closed-bucket hash tables (4) • Java class implementing CBHTs: public class CBHT { private Bucket. Node[] buckets; public CBHT (int m) { buckets = new Bucket. Node[m]; } … // CBHT methods (see below) private int hash (Object key) { return Math. abs(key. hash. Code()) % buckets. length; }

Closed-bucket hash tables (5) • Java class (continued): //// Inner class for CBHT nodes //// private static class Bucket. Node { private Object key, value; private Bucket. Node succ; private Bucket. Node (Object key, Object val, Bucket. Node succ) { … } } }

CBHT search (1) • CBHT search algorithm: To find which if any node of a CBHT contains an entry whose key is equal to target-key: 1. 2. Set b to hash(target-key). Find which if any node of the SLL of bucket b contains an entry whose key is equal to target-key, and terminate with that node as answer.

CBHT search (2) • Implementation (in class CBHT): public Bucket. Node search (Object target. Key) { int b = hash(target. Key); for (Bucket. Node curr = buckets[b]; curr != null; curr = curr. succ) { if (target. Key. equals(curr. key)) return curr; } return null; }

CBHT insertion (1) • CBHT insertion algorithm: To insert the entry (key, val) into a CBHT: 1. 2. 3. Set b to hash(key). Insert the entry (key, val) into the SLL of bucket b, replacing any existing entry whose key is key. Terminate.

CBHT insertion (2) • Implementation (in class CBHT): public void insert (Object key, Object val) { int b = hash(key); for (Bucket. Node curr = buckets[b]; curr != null; curr = curr. succ) { if (key. equals(curr. key)) { curr. value = val; return; } } buckets[b] = new Bucket. Node(key, val, buckets[b]); }

CBHT deletion (1) • CBHT deletion algorithm: To delete the entry (if any) whose key is equal to key from a CBHT: 1. 2. of 3. Set b to hash(key). Delete the entry (if any) whose key is equal to key from the SLL bucket b. Terminate.

CBHT deletion (2) • Implementation (in class CBHT): public void delete (Object key) { int b = hash(key); for (Bucket. Node pred = null, curr = buckets[b]; curr != null; pred = curr, curr = curr. succ) { if (key. equals(curr. key)) { if (pred == null) buckets[b] = curr. succ; else pred. succ = curr. succ; return; } } }

CBHTs: analysis • Analysis of the CBHT search/insertion/deletion algorithms (counting comparisons): Let the number of entries be n. • In the best case, no bucket contains more than (say) 2 entries: Max. no. of comparisons = 2 Best-case time complexity is O(1). • In the worst case, one bucket contains all n entries: Max. no. of comparisons = n Worst-case time complexity is O(n).

CBHTs: design • CBHT design consists of: § choosing the number of buckets m § choosing the hash function hash. • Design aims: § collisions are infrequent § entries are distributed evenly among the buckets, such that few buckets contain more than about 2 entries.

CBHTs: choosing the no. of buckets • The load factor of a hash table is the average number of entries per bucket, n/m. • If n is (roughly) predictable, choose m such that the load factor is likely to be between 0. 5 and 0. 75. § A low load factor wastes space. § A high load factor tends to cause some buckets to have many entries. • Choose m to be a prime number. § Typically the hash function performs modulo-m arithmetic. If m is prime, the entries are more likely to be distributed evenly over the buckets, regardless of any pattern in the keys.

CBHTs: choosing the hash function • The hash function should be efficient (performing few arithmetic operations). • The hash function should distribute the entries evenly among the buckets, regardless of any patterns in the keys. • Possible trade-off: § Speed up the hash function by using only part of the key. § But beware of any patterns in that part of the key.

Example 2: hash table for English words (1) • Suppose that a hash table will contain about 1000 common English words. • Known patterns in the keys: § Letters vary in frequency: • A, E, I, N, S, T are common • Q, X, Z are uncommon. § Word lengths vary in frequency: • word lengths 4– 8 are common • other word lengths are less common.

Example 2 (2) • hash(w) can depend on any of w’s letters and/or length. • Consider m = 20, hash(w) = length of w – 1. – Far too few buckets. Load factor = 1000/20 = 50. – Very uneven distribution. • Consider m = 26, hash(w) = initial letter of w – ‘A’. – Far too few buckets. – Very uneven distribution.

Example 2 (3) • Consider m = 520, hash(w) = 26 (length of w – 1) + (initial letter of w – ‘A’). – Too few buckets. Load factor = 1000/520 1. 9. – Very uneven distribution. Since few words have length 0– 2, buckets 0– 51 will be sparsely populated. Since initial letter Z is uncommon, buckets 25, 51, 77, 103, … will be sparsely populated. And so on. • Consider m = 1499, hash(w) = (weighted sum of letters of w) modulo m i. e. , (c 1 1 st letter of w + c 2 2 nd letter of w + …) modulo m + Good number of buckets. Load factor 0. 67. + Reasonably even distribution.

Open-bucket hash tables (1) • Open-bucket hash table (OBHT): § Each bucket may be occupied by at most one entry. § Whenever there is a collision, displace the new entry to another bucket. • Each bucket has three possible states: § never-occupied (has never contained an entry) § occupied (currently contains an entry) § formerly-occupied (previously contained an entry, which has been deleted and not yet replaced).

Open-bucket hash tables (2) • In the following illustrations, keys are names of chemical elements. Assume: m = 26 hash(e)= (initial letter of e) – ‘A’ • On a collision, insert the new entry in the next unoccupied bucket (treating the array as cyclic).

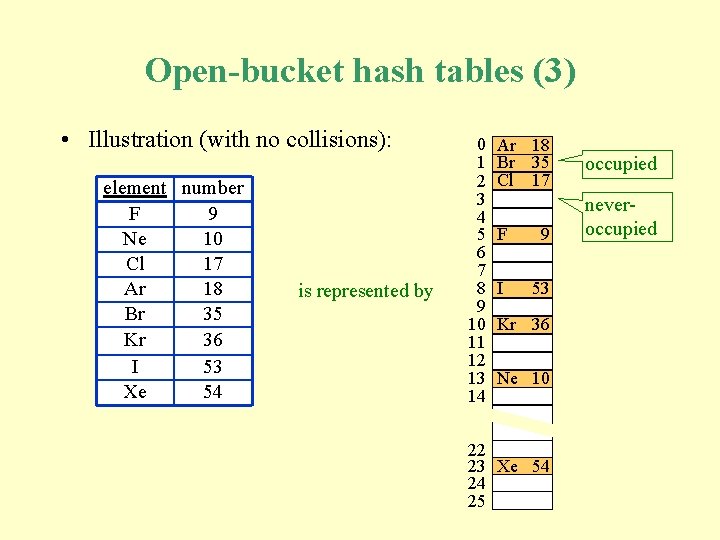
Open-bucket hash tables (3) • Illustration (with no collisions): element number F 9 Ne 10 Cl 17 Ar 18 Br 35 Kr 36 I 53 Xe 54 is represented by 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 Ar 18 Br 35 Cl 17 F 9 I 53 Kr 36 Ne 10 22 23 Xe 54 24 25 occupied neveroccupied

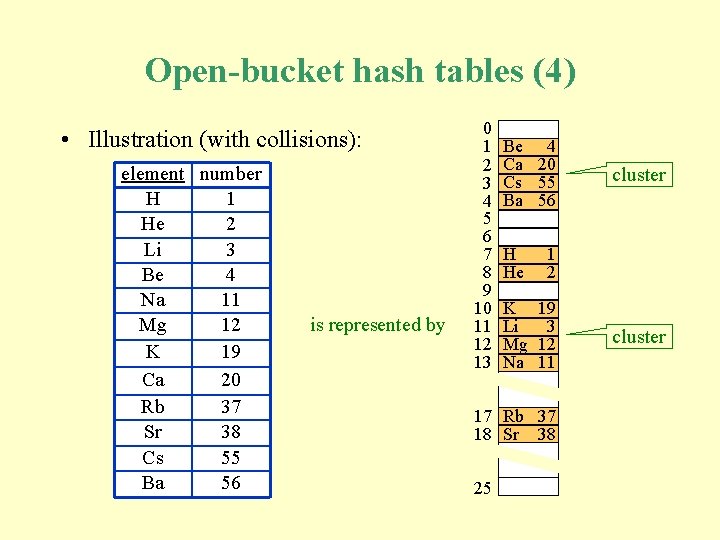
Open-bucket hash tables (4) • Illustration (with collisions): element number H 1 He 2 Li 3 Be 4 Na 11 Mg 12 K 19 Ca 20 Rb 37 Sr 38 Cs 55 Ba 56 is represented by 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Cs 55 Ba 56 H He 1 2 K 19 Li 3 Mg 12 Na 11 17 Rb 37 18 Sr 38 25 cluster

Open-bucket hash tables (5) • Java class implementing OHBTs: public class OBHT { private Bucket. Entry[] buckets; public OBHT (int m) { buckets = new Bucket. Entry[m]; } OBHT methods … private int hash (Object k) { return Math. abs(k. hash. Code()) % buckets. length; }

Open-bucket hash tables (6) • Java class (continued): //// Inner class for OBHT entries //// private static class Bucket. Entry { private Object key, value; private Bucket. Entry (Object k, Object v) { this. key = k; this. value = v; } private static final Bucket. Entry FORMER = new Bucket. Entry(null, null);

Example 3: populating an OBHT • Animation: element number H 1 He 2 Li 3 Be 4 Na 11 Mg 12 K 19 Ca 20 Rb 37 Sr 38 Cs 55 Ba 56 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Cs 55 Ba 56 H He 1 2 K 19 Li 3 Mg 12 Na 11 17 Rb 37 18 Sr 38 25

OBHT search (1) • OBHT search algorithm: To find which if any bucket of an OBHT is occupied by an entry whose key is equal to target-key: 1. 2. Set b to hash(target-key). Repeat: 2. 1. If bucket b is never-occupied: 2. 1. 1. Terminate with answer none. 2. 2. If bucket b is occupied by an entry whose key is equal to target-key: 2. 2. 1. Terminate with answer b. 2. 3. If bucket b is formerly-occupied, or is occupied by an entry whose key is not equal to target-key: 2. 3. 1. Increment b modulo m.

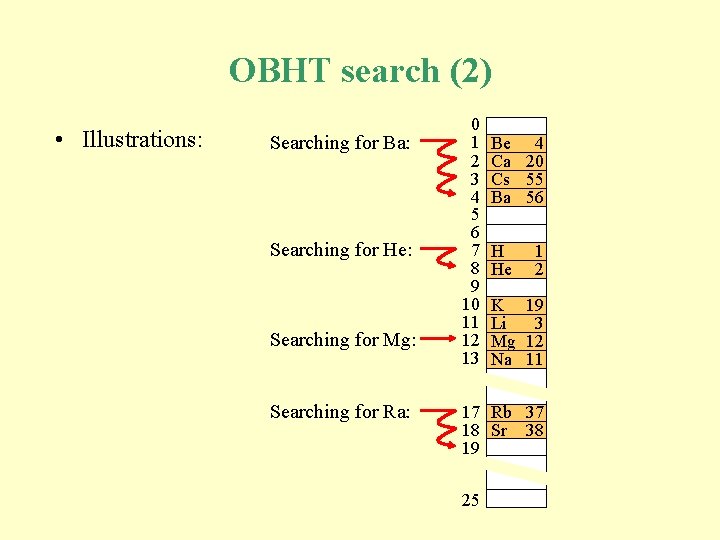
OBHT search (2) • Illustrations: Searching for Ba: Searching for He: Searching for Mg: Searching for Ra: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Cs 55 Ba 56 H He 1 2 K 19 Li 3 Mg 12 Na 11 17 Rb 37 18 Sr 38 19 25

OBHT search (3) • Implementation (in class OBHT): public int search (Object target. Key) { int b = hash(target. Key); for (; ; ) { Bucket. Entry old = buckets[b]; if (old == null) return NONE; else if (old != Bucket. Entry. FORMER && target. Key. equals(old. key)) return b; else b = (b + 1) % buckets. length; } }

OBHT insertion (1) • OBHT insertion algorithm: To insert the entry (key, val) into an OBHT: 1. 2. Set b to hash(key). Repeat: 2. 1. If bucket b is never-occupied: 2. 1. 1. If bucket b is the last never-occupied bucket, treat the OBHT as full. 2. 1. 2. Make bucket b occupied by (key, val). 2. 1. 3. Terminate. 2. 2. If bucket b is formerly-occupied, or is occupied by an entry whose key is equal to key: 2. 2. 1. Make bucket b occupied by (key, val). 2. 2. 2. Terminate. 2. 3. …

OBHT insertion (2) • OBHT insertion algorithm (continued): 2. 3. equal to If bucket b is occupied by an entry whose key is not key: 2. 3. 1. Increment b modulo m.

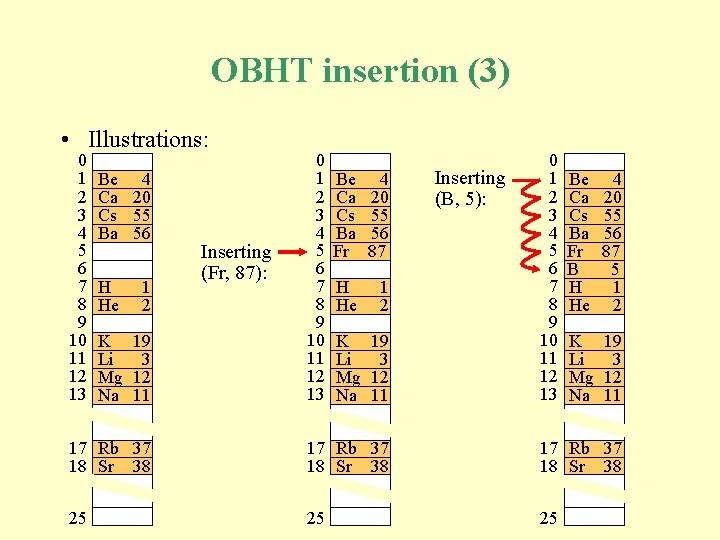
OBHT insertion (3) • Illustrations: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Cs 55 Ba 56 H He 1 2 K 19 Li 3 Mg 12 Na 11 Inserting (Fr, 87): 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be Ca Cs Ba Fr 4 20 55 56 87 H He 1 2 K 19 Li 3 Mg 12 Na 11 Inserting (B, 5): 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be Ca Cs Ba Fr B H He 4 20 55 56 87 5 1 2 K 19 Li 3 Mg 12 Na 11 17 Rb 37 18 Sr 38 25 25 25

OBHT insertion (4) • Implementation (in class OBHT): private int load = 0; // no. of occupied or formerly// occupied buckets in this OBHT public void insert (Object key, Object val) { Bucket. Entry newest = new Bucket. Entry(key, val); int b = hash(key); for (; ; ) { Bucket. Entry old = buckets[b]; if (old == null) { if (++load == buckets. length) …; buckets[b] = newest; return;

OBHT insertion (5) • Implementation (continued): } else if (old == Bucket. Entry. FORMER || key. equals(old. key)) { buckets[b] = newest; return; } else b = (b + 1) % buckets. length; } }

OBHT deletion (1) • OBHT deletion algorithm: To delete the entry (if any) whose key is equal to key from an OBHT: 1. 2. Set b to hash(key). Repeat: 2. 1. If bucket b is never-occupied: 2. 1. 1. Terminate. 2. 2. If bucket b is occupied by an entry whose key is equal to key: 2. 3. 2. 2. 1. Make bucket b formerly-occupied. 2. 2. 2. Terminate. If bucket b is formerly-occupied, or is occupied by an entry whose key is not equal to key: 2. 3. 1. Increment b modulo m.

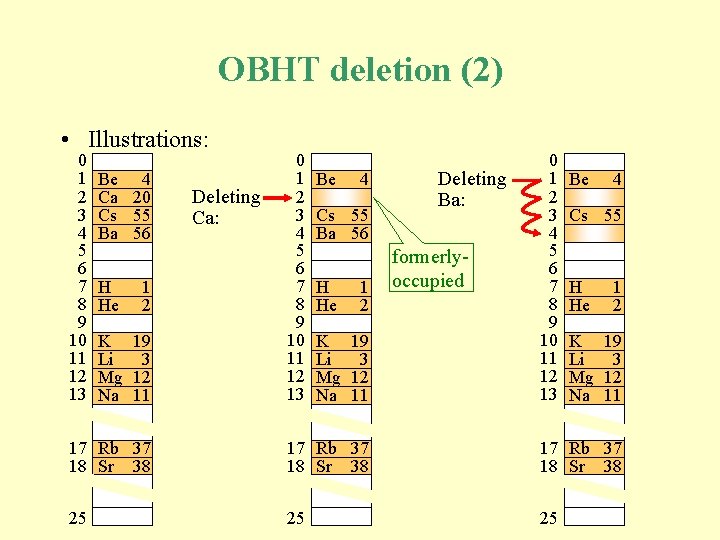
OBHT deletion (2) • Illustrations: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Cs 55 Ba 56 H He 1 2 K 19 Li 3 Mg 12 Na 11 Deleting Ca: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Cs 55 Ba 56 H He 1 2 K 19 Li 3 Mg 12 Na 11 Deleting Ba: formerlyoccupied 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Cs 55 H He 1 2 K 19 Li 3 Mg 12 Na 11 17 Rb 37 18 Sr 38 25 25 25

OBHT deletion (3) • Implementation (in class OBHT): public void delete (Object key) { int b = hash(key); for (; ; ) { Bucket. Entry old = buckets[b]; if (old == null) return; else if (old != Bucket. Entry. FORMER && key. equals(old. key)) { buckets[b] = Bucket. Entry. FORMER; return; } else b = (b + 1) % buckets. length; } }

OBHTs: analysis • Analysis of OBHT search/insertion/deletion algorithm (counting comparisons): Let the number of entries be n. • In the best case, no cluster contains more than (say) 4 entries: Max. no. of comparisons = 4 Best-case time complexity is O(1). • In the worst case, one cluster contains all n entries: Max. no. of comparisons = n Worst-case time complexity is O(n).

OBHTs: design • OBHT design consists of: § choosing the number of buckets m § choosing the hash function hash § choosing the step length s (explained later). • Design aims: § collisions are infrequent § entries are distributed evenly over the hash table, such that few clusters contain more than about 4 entries.

OBHTs: choosing the no. of buckets • Recall: The load factor of a hash table is the average number of entries per bucket, n/m. • If n is (roughly) predictable, choose m such that the load factor is likely to be between 0. 5 and 0. 75. § A low load factor wastes space. § A high load factor tends to result in long clusters. • Choose m to be a prime number.

OBHTs: choosing the hash function • The hash function should be efficient. • The hash function should distribute the entries evenly over the buckets, with few long clusters. § In an OHBT with s = 1, a cluster will form when several entries fall into the same or adjacent buckets.

OBHTs: choosing the step length • To resolve a collision, the search/insertion/deletion algorithm increments the bucket index and tries again. • The step length, s, is the amount by which the bucket index is incremented. So far we have assumed s = 1. • Alternatively, we can use a fixed s > 1. • Choose m to be prime, and choose s to be in the range 2…m– 1. § This ensures that s and m have no common factors. § Otherwise, if (say) m = 10 and s = 2, a typical search path would be 6– 8– 0– 2– 4, never reaching the remaining buckets!

OBHTs: double hashing (1) • Better still, let different keys have different step lengths. (But each key always has the same step length. ) • Double hashing: To search/insert/delete key k, compute s from k, using a second hash function s = step(k). • In the following illustration, keys are names of chemical elements. Assume: m = hash(e)= step(e) = 23 (initial letter of e – ‘A’) modulo m 1, if e has a single letter, otherwise 2 + (second letter of e – ‘a’) modulo 21

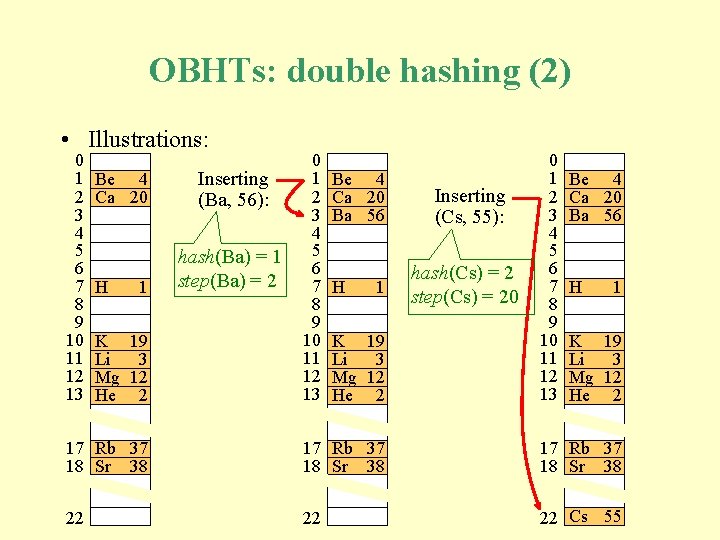
OBHTs: double hashing (2) • Illustrations: 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 H 1 K 19 Li 3 Mg 12 He 2 Inserting (Ba, 56): hash(Ba) = 1 step(Ba) = 2 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Ba 56 H 1 K 19 Li 3 Mg 12 He 2 Inserting (Cs, 55): hash(Cs) = 2 step(Cs) = 20 0 1 2 3 4 5 6 7 8 9 10 11 12 13 Be 4 Ca 20 Ba 56 H 1 K 19 Li 3 Mg 12 He 2 17 Rb 37 18 Sr 38 22 22 22 Cs 55

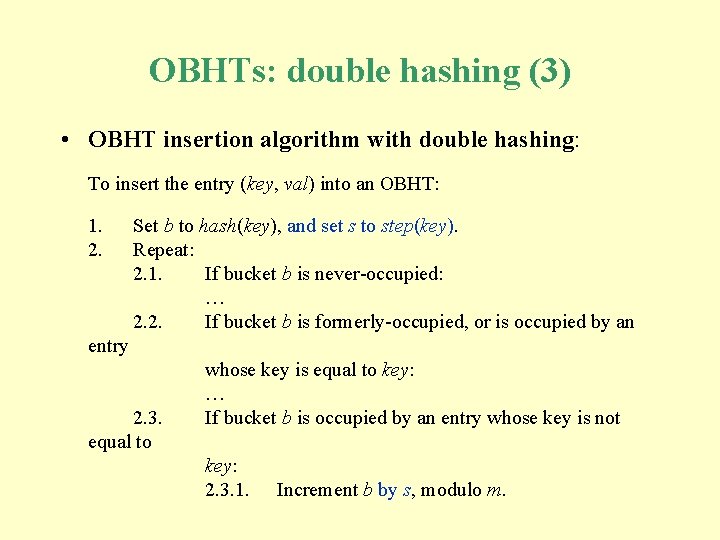
OBHTs: double hashing (3) • OBHT insertion algorithm with double hashing: To insert the entry (key, val) into an OBHT: 1. 2. Set b to hash(key), and set s to step(key). Repeat: 2. 1. If bucket b is never-occupied: … 2. 2. If bucket b is formerly-occupied, or is occupied by an entry 2. 3. equal to whose key is equal to key: … If bucket b is occupied by an entry whose key is not key: 2. 3. 1. Increment b by s, modulo m.

Hash tables in practice (1) • The following trials compare the performance of three hash tables, each with m buckets: § a CBHT § an OHBT with step length s = 1 § an OHBT with step length s determined by double hashing. • The hash function distributes keys uniformly among the buckets (i. e. , the probability that a key is mapped to any particular bucket is 1/m). • In each trial, all three hash tables are loaded with the same set of n randomly-generated keys.

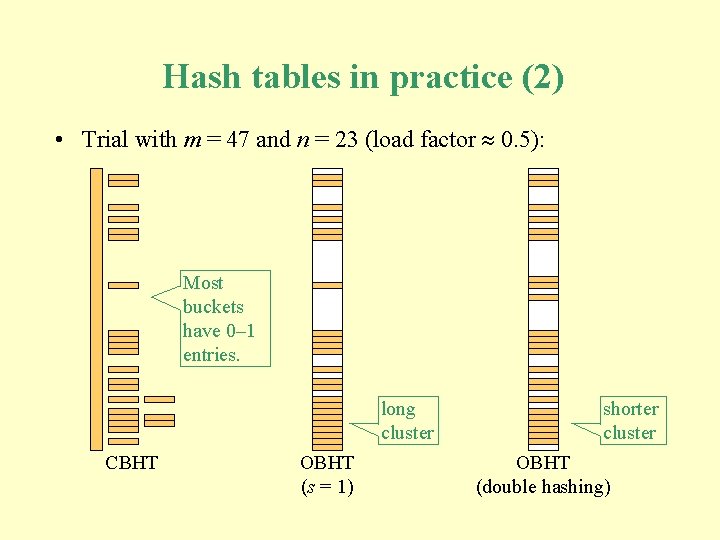
Hash tables in practice (2) • Trial with m = 47 and n = 23 (load factor 0. 5): Most buckets have 0– 1 entries. long cluster CBHT OBHT (s = 1) shorter cluster OBHT (double hashing)

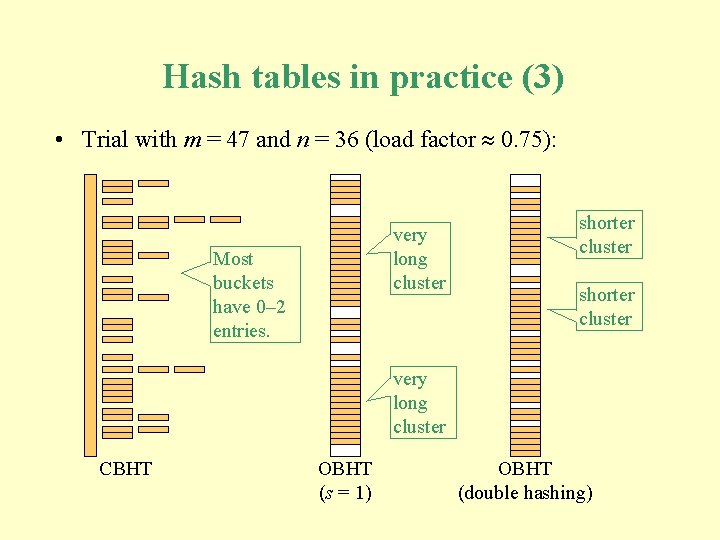
Hash tables in practice (3) • Trial with m = 47 and n = 36 (load factor 0. 75): very long cluster Most buckets have 0– 2 entries. shorter cluster very long cluster CBHT OBHT (s = 1) OBHT (double hashing)

Example 4: hash table for student records (1) • Consider a hypothetical university’s student records. About 1500 new students register each year, and most students stay for 4 years. • Each student has a unique id, of the form yydddd (where yy are the last two digits of the year of first registration, and where dddd is a serial number). • Suppose that the student records will be held in a hash table. • hash(id) can depend on any or all of id’s digits.

Example 4 (2) • Consider m = 100, hash(id) = first two digits of id. – Far too few buckets. Load factor 6000/100 60. – Very uneven distribution. E. g. , in academic year 2001– 02, most ids start with 98, 99, 00, or 01. • Consider m = 10000, hash(id) = last four digits of id. + Good number of buckets. Load factor 6000/10000 0. 6. – Uneven distribution. Most ids end with 0000… 1500. • Consider m = 9997, hash(id) = id modulo m. + Good number of buckets. Load factor 6000/9997 0. 6. – Even distribution (since m is prime).

Example 4 (3) • Consider OBHT with s = 1. – Four clusters of about 1500 entries. • Consider OBHT with s = 2000. + Should avoid clustering. • Consider OBHT with double hashing. + Should avoid clustering.

Implementations of sets using CBHTs • Similar to implementation of maps (with set members instead of map entries). • Summary of algorithms: Operation Algorithm Time complexity contains CBHT search O(1) O(n) best worst add CBHT insertion O(1) O(n) best worst remove CBHT deletion O(1) O(n) best worst

Implementations of maps using CBHTs • Summary of algorithms: Operation Algorithm Time complexity get CBHT search O(1) O(n) best worst remove CBHT deletion O(1) O(n) best worst put CBHT insertion O(1) O(n) best worst put. All merge on corresponding buckets of both CBHTs O(m) O(n 1 n 2) best worst equals equality test on corresponding O(m) buckets of both CBHTs O(n 1 n 2) best worst