12 7 Dilations Objective Identify and draw dilations

12 -7 Dilations Objective Identify and draw dilations. Holt Geometry

12 -7 Dilations Recall that a dilation is a transformation that changes the size of a figure but not the shape. The image and the preimage of a figure under a dilation are similar. Holt Geometry

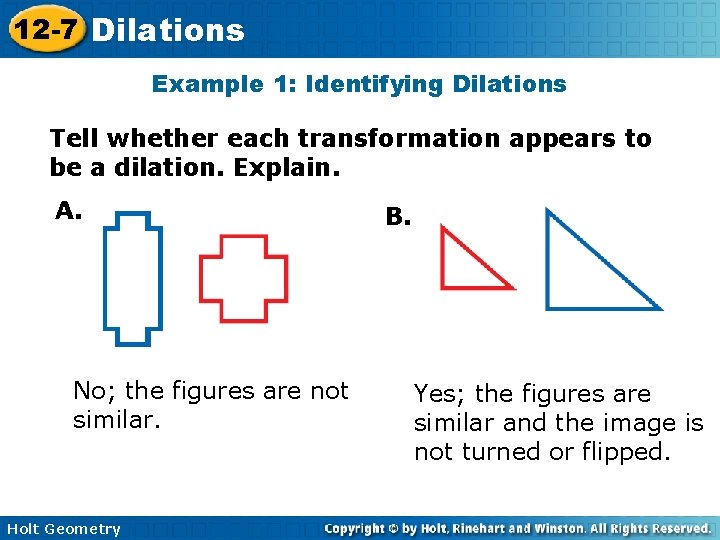
12 -7 Dilations Example 1: Identifying Dilations Tell whether each transformation appears to be a dilation. Explain. A. No; the figures are not similar. Holt Geometry B. Yes; the figures are similar and the image is not turned or flipped.

12 -7 Dilations Example 1 a Tell whether each transformation appears to be a dilation. Explain. a. b. No, the figures are not similar. Holt Geometry Yes, the figures are similar and the image is not turned or flipped.

12 -7 Dilations A dilation enlarges or reduces all dimensions proportionally. A dilation with a scale factor greater than 1 is an enlargement, or expansion. A dilation with a scale factor greater than 0 but less than 1 is a reduction, or contraction. Holt Geometry

12 -7 Dilations Holt Geometry

12 -7 Dilations If the scale factor of a dilation is negative, the preimage is rotated by 180°. For k > 0, a dilation with a scale factor of –k is equivalent to the composition of a dilation with a scale factor of k that is rotated 180° about the center of dilation. Holt Geometry

12 -7 Dilations Example 2: Drawing Dilations in the Coordinate Plane Draw the image of the triangle with vertices P(– 4, 4), Q(– 2, – 2), and R(4, 0) under a dilation with a scale factor of origin. The dilation of (x, y) is Holt Geometry centered at the

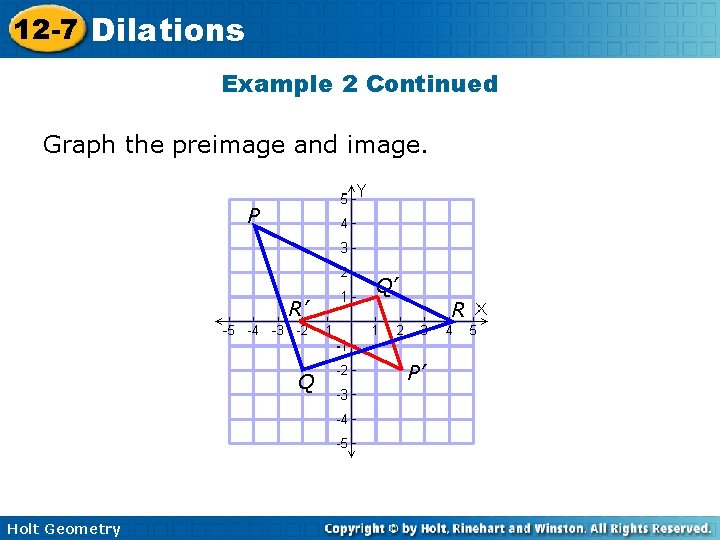
12 -7 Dilations Example 2 Continued Graph the preimage and image. P R’ Q Holt Geometry Q’ R P’