12 5 Permutations and combinations Geometry How can

12. 5 Permutations and combinations. Geometry How can find the number of ways in which two or more events can occur?

Directions: Make an organized list of all the possible four-letter arrangements using the letters “M” “A” “T” “H” MATH AMTH TMAH MAHT MTHA AMHT AHTM TMHA THMA HTAM HATM MTAH AHMT THAM HAMT MHTA ATMH TAMH HMAT MHAT ATHM TAHM HMTA 4! 4 factorial 4 x 3 x 2 x 1 = 24 arrangements. Geometry 12. 5 permutations and combinations

Vocabulary: Permutation: An arrangement in which order matters is important is called a permutation. EX: John, Steve and Mark are running in a race. How many different ways can they finish in 1 st, 2 nd or 3 rd place. JSM JMS SJM 3 Factorial 3! = 3 x 2 x 1 = 6 Geometry 12. 5 permutations and combinations SMJ MJS MSJ

Permutations (when the order matters) Example: Six people are running in a race. The top three places get 1 st, 2 nd, and 3 rd prize. How many arrangements are there? How many people have a shot at…. 2 nd 1 st 6 • 5 Permutation notation 3 rd • 4 = 120 arrangements means a group of 6 taken 3 at a time. Geometry 12. 5 permutations and combinations

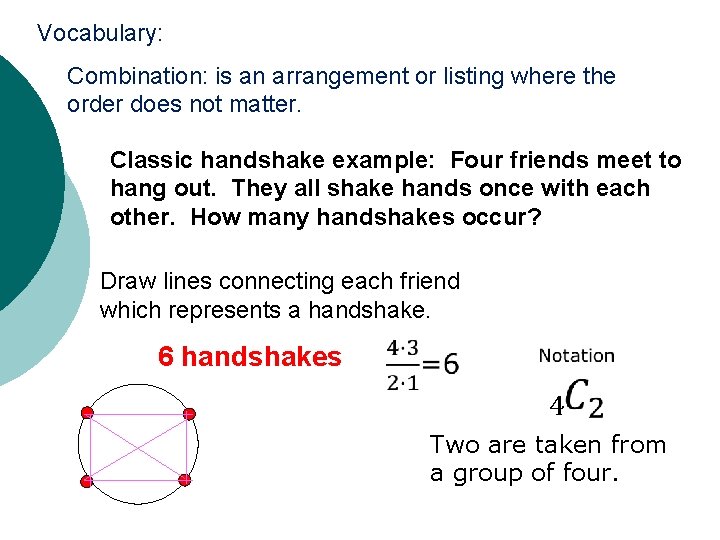
Vocabulary: Combination: is an arrangement or listing where the order does not matter. Classic handshake example: Four friends meet to hang out. They all shake hands once with each other. How many handshakes occur? Draw lines connecting each friend which represents a handshake. 6 handshakes 4 Two are taken from a group of four.

Combinations: When the order does not matter Six People are running for city council. There are three positions available. How many combinations are there? Hint Use A, B, C, D, E, F ABC ABD ABE ABF ACD ACE ACF ADE ADF AEF BCD BCE BCF for the six candidates BDE BDF BEF CDE CDF CEF DEF 20 DIFFERENT COMBINATIONS Mathematically 120 6 = 20 6 When the order does not matters, you must divide! Geometry 12. 5 permutations and combinations

Example: You just bought 5 books and want to take two of them with you on vacation. How many different combinations of two books can you take? Hint: Use A, B, C, D, E for each book AB AC AD AE BC BD BE CD CE DE MATHEMATICALLY 10 COMBINATIONS Geometry 12. 5 permutations and combinations 20 2 = 10