12 3 Example A 1 5 m tall

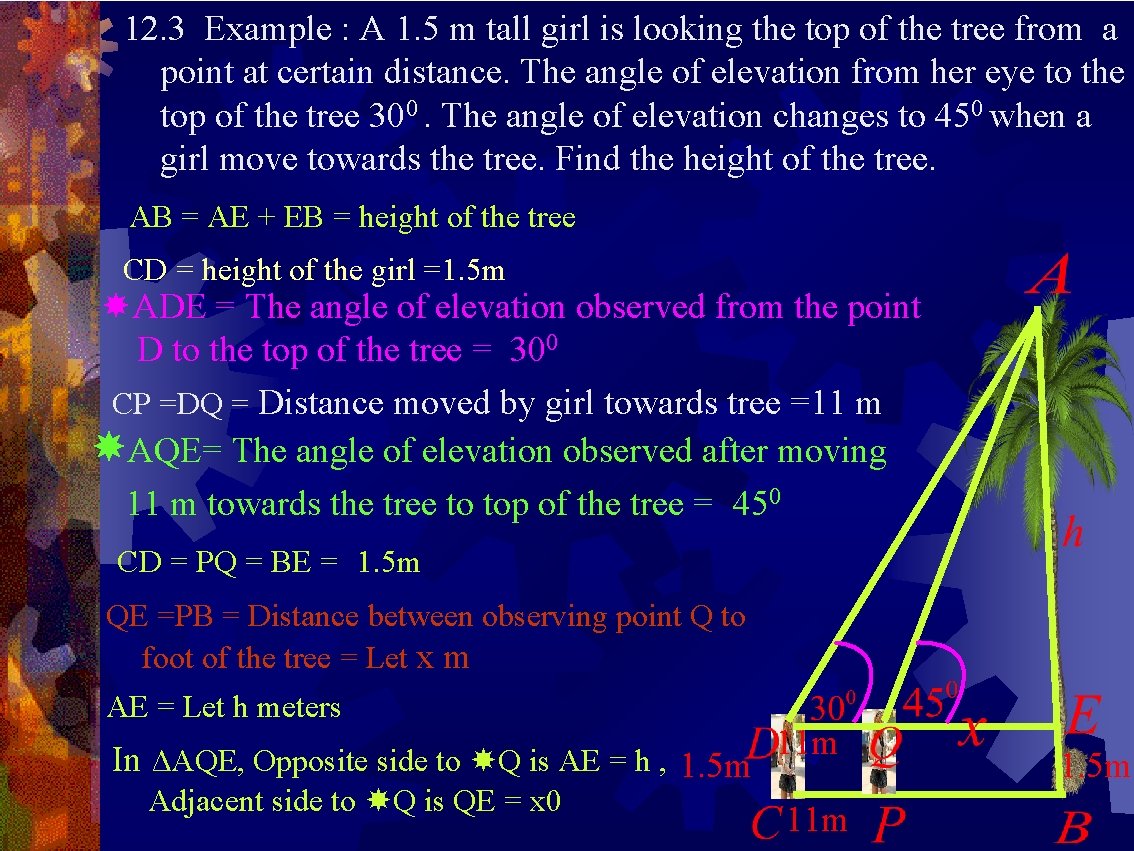
12. 3 Example : A 1. 5 m tall girl is looking the top of the tree from a point at certain distance. The angle of elevation from her eye to the top of the tree 300. The angle of elevation changes to 450 when a girl move towards the tree. Find the height of the tree. AB = AE + EB = height of the tree CD = height of the girl =1. 5 m ADE = The angle of elevation observed from the point D to the top of the tree = 300 CP =DQ = Distance moved by girl towards tree =11 m AQE= The angle of elevation observed after moving 11 m towards the tree to top of the tree = 450 CD = PQ = BE = 1. 5 m QE =PB = Distance between observing point Q to foot of the tree = Let x m AE = Let h meters In ΔAQE, Opposite side to Q is AE = h , 1. 5 m Adjacent side to Q is QE = x 0 11 m 1. 5 m

In ΔADE, Opposite side to D is AE=h , Adjacent side to D is DE = 11 + x AB = AE + EB = AB = h+1. 5 =15. 026+1. 5 = 16. 526 m height of the tree = 16. 526 m

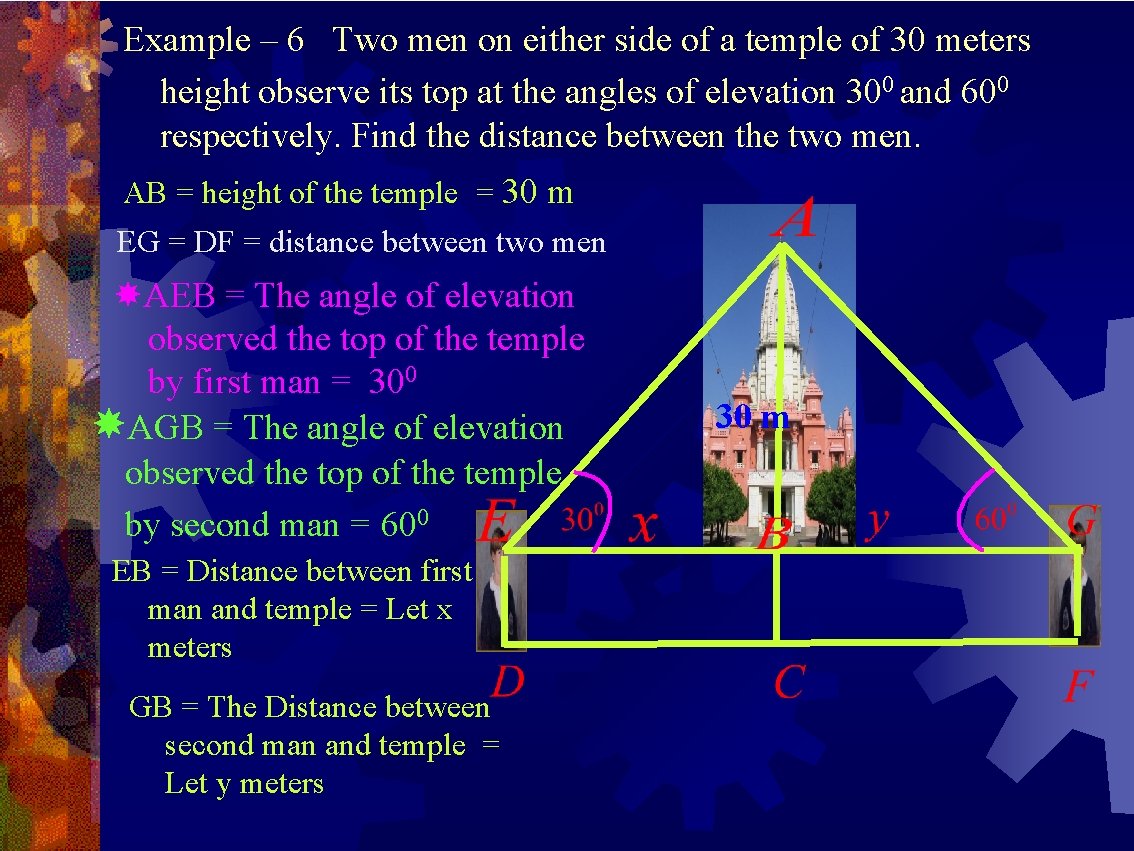
Example – 6 Two men on either side of a temple of 30 meters height observe its top at the angles of elevation 300 and 600 respectively. Find the distance between the two men. AB = height of the temple = 30 m EG = DF = distance between two men AEB = The angle of elevation observed the top of the temple by first man = 300 AGB = The angle of elevation observed the top of the temple by second man = 600 EB = Distance between first man and temple = Let x meters GB = The Distance between second man and temple = Let y meters 30 m

In ΔAEB, Opposite side to E is AB, Adjacent side to E is EB In ΔAGB, Opposite side to G is AB , Adjacent side to G is BG EG= x + y = Distance between two men m

Example – 7 A Straight highway leads to the foot of a tower. Ramaiah standing at the top of the tower observes a car at angle of depression 300. The car is approaching the foot of the tower with a uniform speed. Six seconds later, the angle of depression of the car is found to be 600. Find the time taken by the car to reach the foot of the tower from this point. AB = height of the tower = Let h meters EBC = BCA = The angle of depression Ramaiah standing on the top of the tower observes a car = 300 CD =Distance travelled by car in 6 Seconds = Let x meters The angle of depression observed Six seconds later to the uniform speed car = 600 Distance to be travelled to reach the foot of the tower = Let d meters

In ΔABD, Opposite side to D is AB =h , Adjacent side to D is AD = d Time taken to travel x meter = 6 Seconds Time taken to travel x / 2 meters = 6/2 = 3 Seconds In ΔABC, Opposite to C is AB = h , Adjacent side to C is AC = x +d The time taken by the car to reach the foot of the tower from the point = 3 Seconds

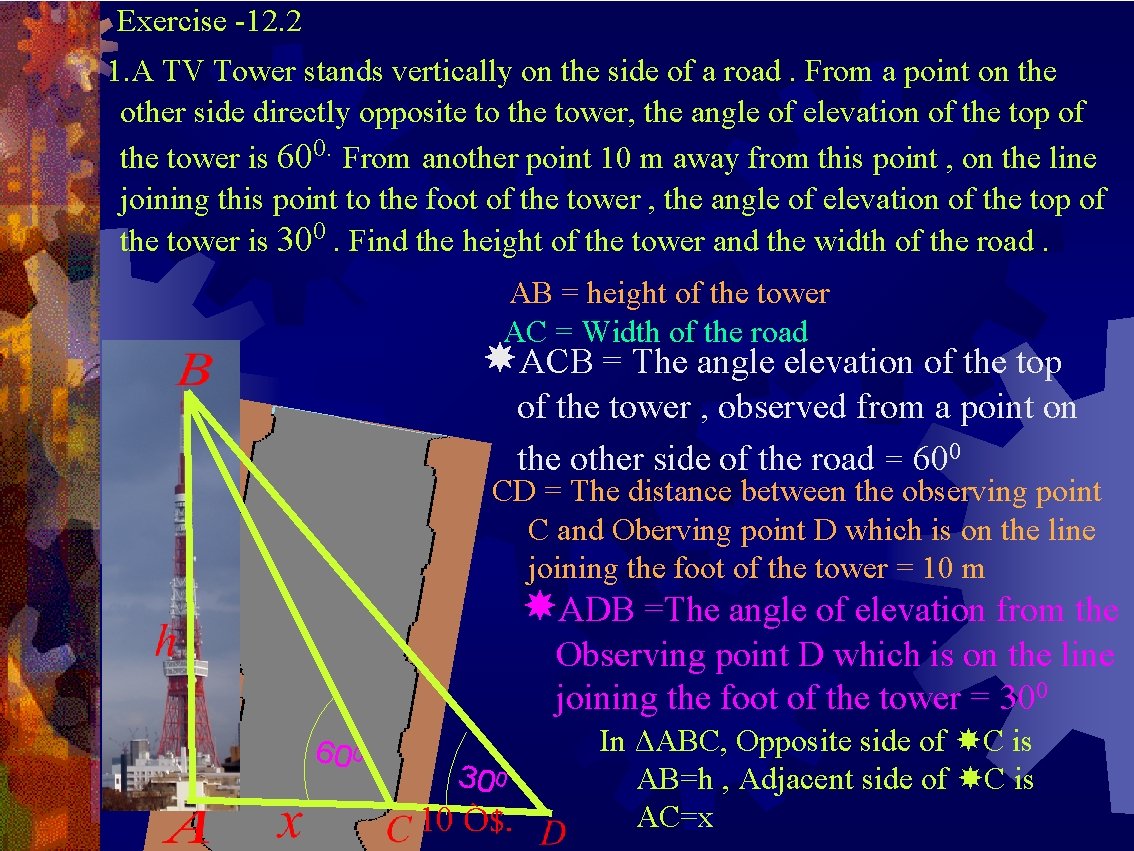
Exercise -12. 2 1. A TV Tower stands vertically on the side of a road. From a point on the other side directly opposite to the tower, the angle of elevation of the top of the tower is 600. From another point 10 m away from this point , on the line joining this point to the foot of the tower , the angle of elevation of the top of the tower is 300. Find the height of the tower and the width of the road. AB = height of the tower AC = Width of the road ACB = The angle elevation of the top of the tower , observed from a point on the other side of the road = 600 CD = The distance between the observing point C and Oberving point D which is on the line joining the foot of the tower = 10 m ADB =The angle of elevation from the Observing point D which is on the line joining the foot of the tower = 300 60 0 30 0 10 Ò$. In ΔABC, Opposite side of C is AB=h , Adjacent side of C is AC=x

In ΔABD, Opposide to D is AB=h, Adjacent side to D is AD = x+10 AC = Width of the road = x = 5 meters AB = height of the tower = h = 8. 66 meters

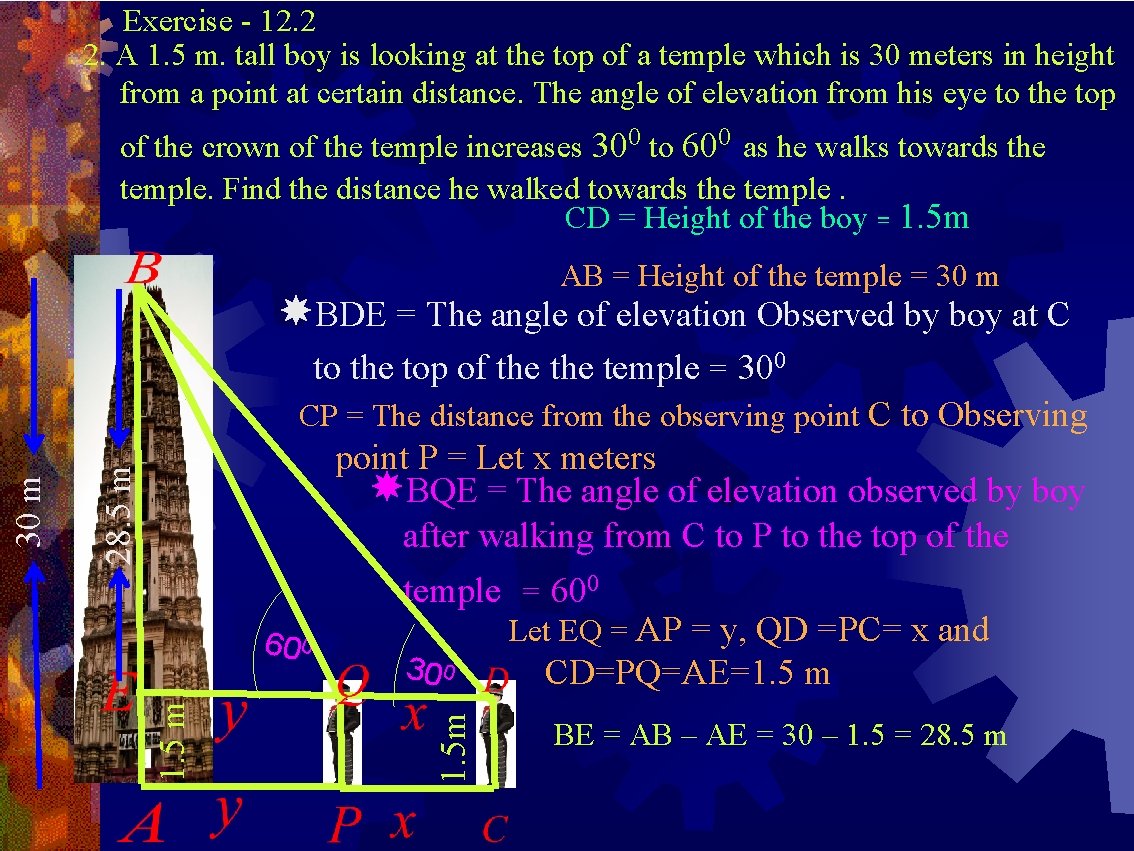
Exercise - 12. 2 2. A 1. 5 m. tall boy is looking at the top of a temple which is 30 meters in height from a point at certain distance. The angle of elevation from his eye to the top of the crown of the temple increases 300 to 600 as he walks towards the temple. Find the distance he walked towards the temple. CD = Height of the boy = 1. 5 m AB = Height of the temple = 30 m BDE = The angle of elevation Observed by boy at C to the top of the temple = 300 point P = Let x meters BQE = The angle of elevation observed by boy after walking from C to P to the top of the 28. 5 m temple = 600 Let EQ = AP = y, QD =PC= x and 30 0 1. 5 m 60 0 1. 5 m 30 m CP = The distance from the observing point C to Observing CD=PQ=AE=1. 5 m BE = AB – AE = 30 – 1. 5 = 28. 5 m

In Δ BQE , Opposite side to Q is AB= 28. 5 m and Adjacent side to Q is QE = y In Δ BDE , Opposite side to D is AB=28. 5 m , Adjacent side D is DE = DQ+EQ = x + y The distance , boy walked towards the temple = 32. 908 m

Exercise - 12. 2 3. A Statue stands on the top of a 2 m tall pedestal. From a point on the ground , the angle of elevation of the top of the stature is 600 and from the same point , the angle of elevation of the top of the pedestal is 450. Find the height of the statue. hm. AB = Height of the pedestal = 2 m BC = Height of the statue = Let h meters AD = The distance between the observing point D on the ground to bottom of the pedestal A = Let x meters ADC =The angle of elevation from the observing 2 m point D to the top of the statue= 600 ADB = The angle of elevation from the observing point D to the top of te pedestal = 450 60 0 45 0 In Δ ABD , opposite side to D is AB=2 m , Adjacent side to D is AD = Let x

In Δ ACD, Opposite side to D is AC = 2+h , Adjacent side to D is AD = x BC = Height of the statue = 1. 464 m

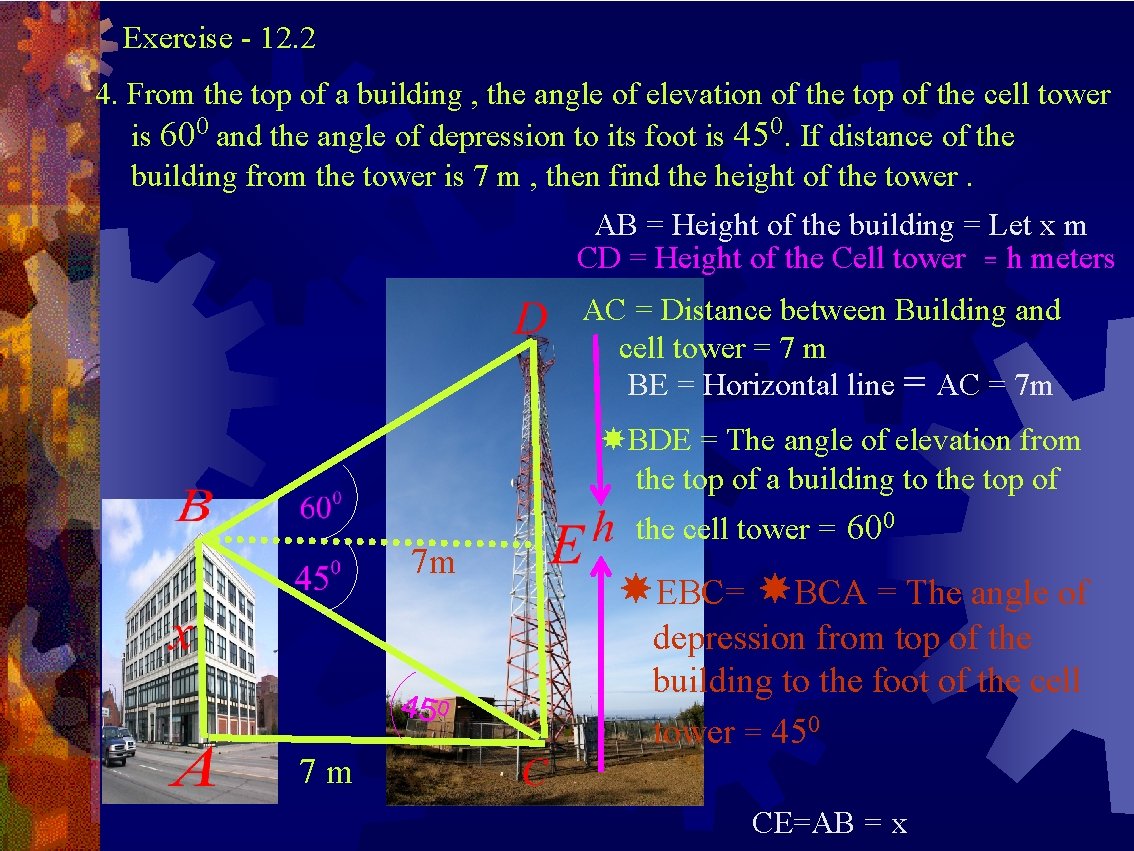
Exercise - 12. 2 4. From the top of a building , the angle of elevation of the top of the cell tower is 600 and the angle of depression to its foot is 450. If distance of the building from the tower is 7 m , then find the height of the tower. AB = Height of the building = Let x m CD = Height of the Cell tower = h meters AC = Distance between Building and cell tower = 7 m BE = Horizontal line = AC = 7 m BDE = The angle of elevation from the top of a building to the top of 7 m 45 0 7 m the cell tower = 600 EBC= BCA = The angle of depression from top of the building to the foot of the cell tower = 450 CE=AB = x

In Δ ABC , Opposite side to C is AB = x , Adjacent side to C is AC = 7 m In Δ BED, Opposite side to B is DE = CD – CE = h – x , Adjacent side to B is BE = 7 m CD = Height of the cell tower = 19. 124 m

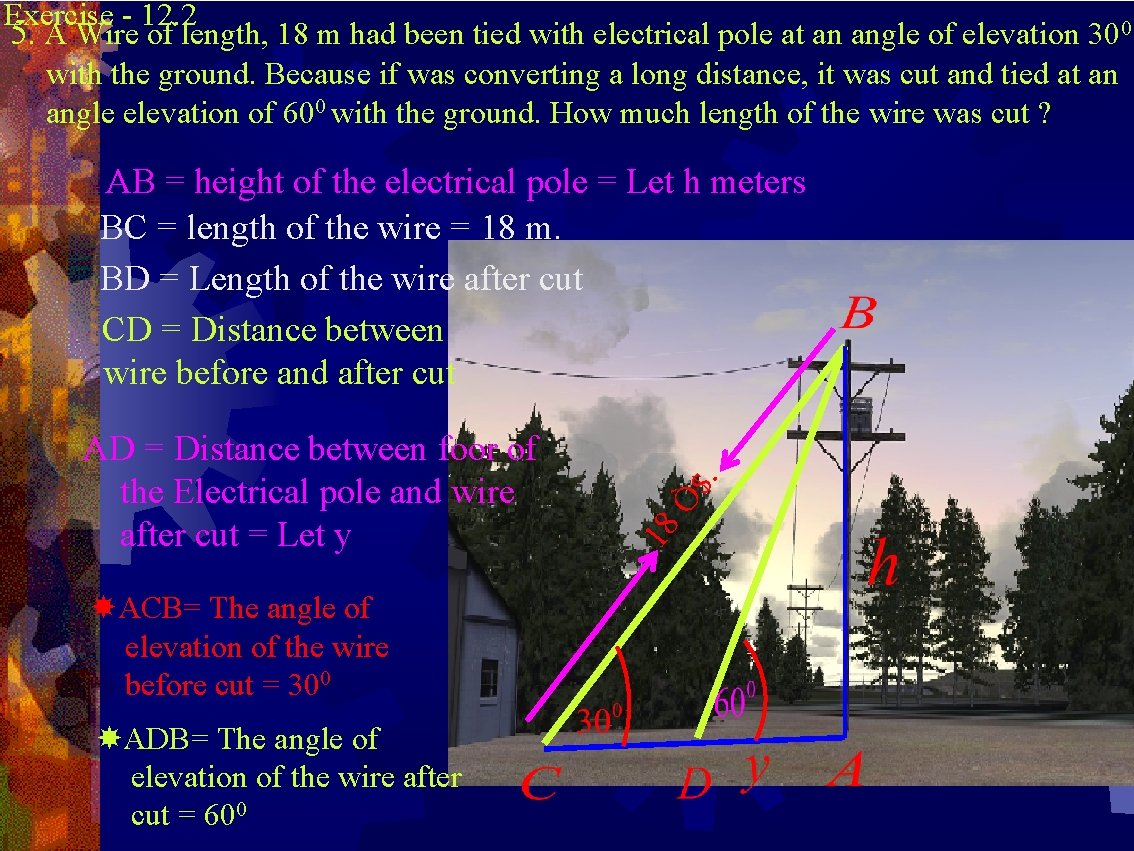
Exercise - 12. 2 5. A Wire of length, 18 m had been tied with electrical pole at an angle of elevation 300 with the ground. Because if was converting a long distance, it was cut and tied at an angle elevation of 600 with the ground. How much length of the wire was cut ? ACB= The angle of elevation of the wire before cut = 300 ADB= The angle of elevation of the wire after cut = 600 18 AD = Distance between foor of the Electrical pole and wire after cut = Let y Ò$. AB = height of the electrical pole = Let h meters BC = length of the wire = 18 m. BD = Length of the wire after cut CD = Distance between wire before and after cut

In ΔABC, Opposite side to C is AB, Adjacent side to C is AC, hypotenuse is AC In ΔABD, Opposite side to D is AB , Adacent side to D is AD, hypotenuse is BD The length of the wire was cut = BC – BD = 18 – 10. 392 = 7. 608 meters

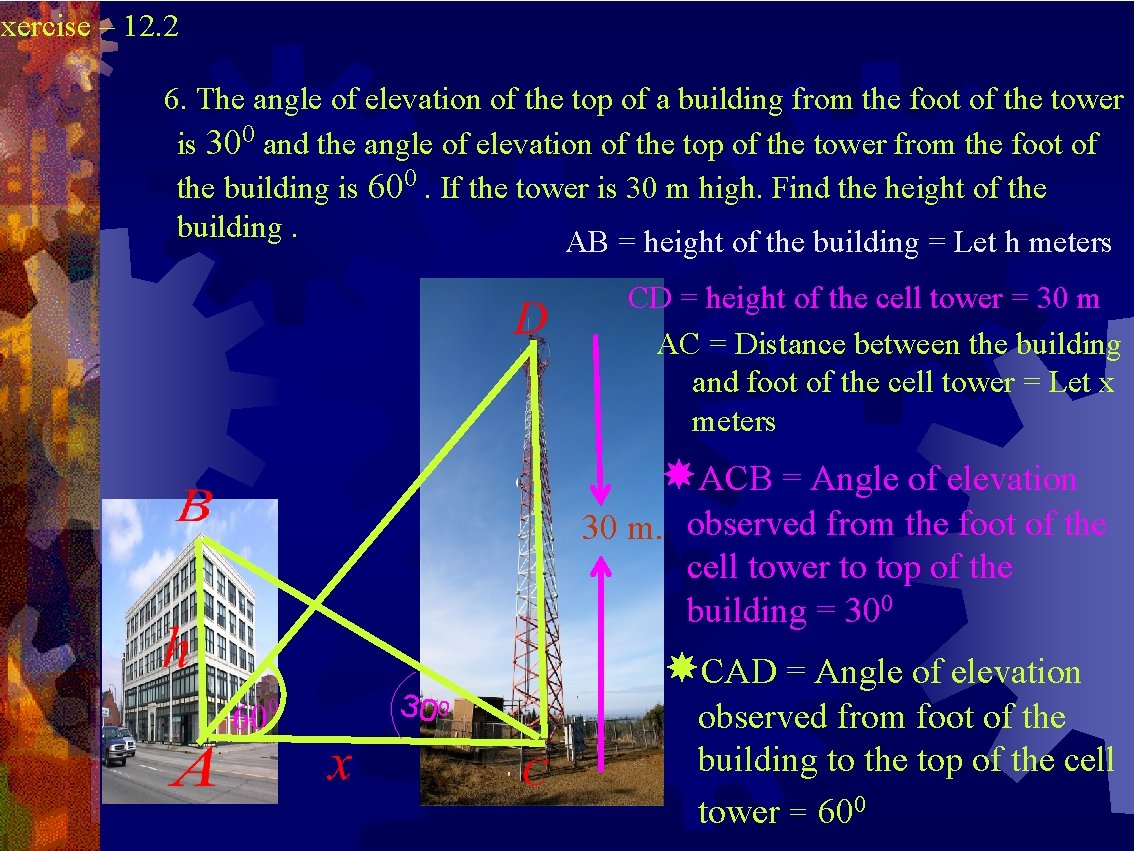
Exercise – 12. 2 6. The angle of elevation of the top of a building from the foot of the tower is 300 and the angle of elevation of the top of the tower from the foot of the building is 600. If the tower is 30 m high. Find the height of the building. AB = height of the building = Let h meters CD = height of the cell tower = 30 m AC = Distance between the building and foot of the cell tower = Let x meters ACB = Angle of elevation 30 m. observed from the foot of the cell tower to top of the building = 300 30 0 CAD = Angle of elevation observed from foot of the building to the top of the cell tower = 600

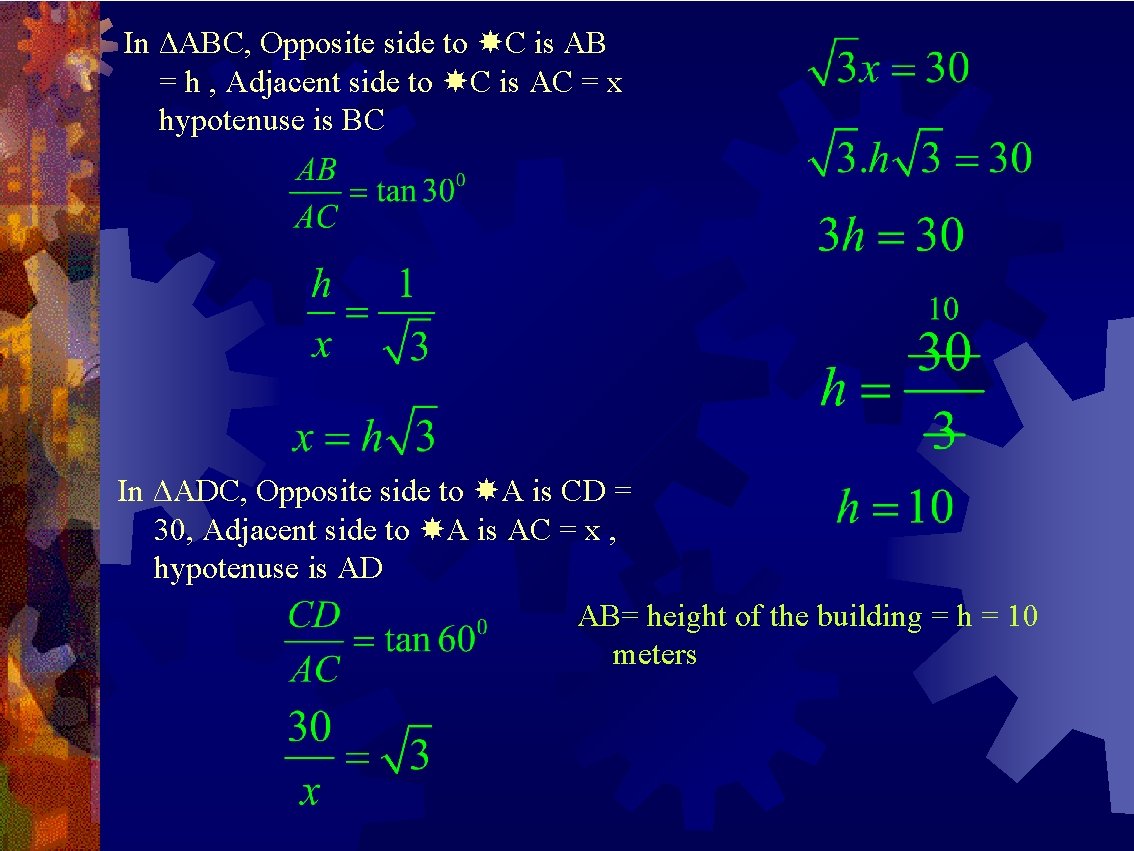
In ΔABC, Opposite side to C is AB = h , Adjacent side to C is AC = x hypotenuse is BC In ΔADC, Opposite side to A is CD = 30, Adjacent side to A is AC = x , hypotenuse is AD AB= height of the building = h = 10 meters

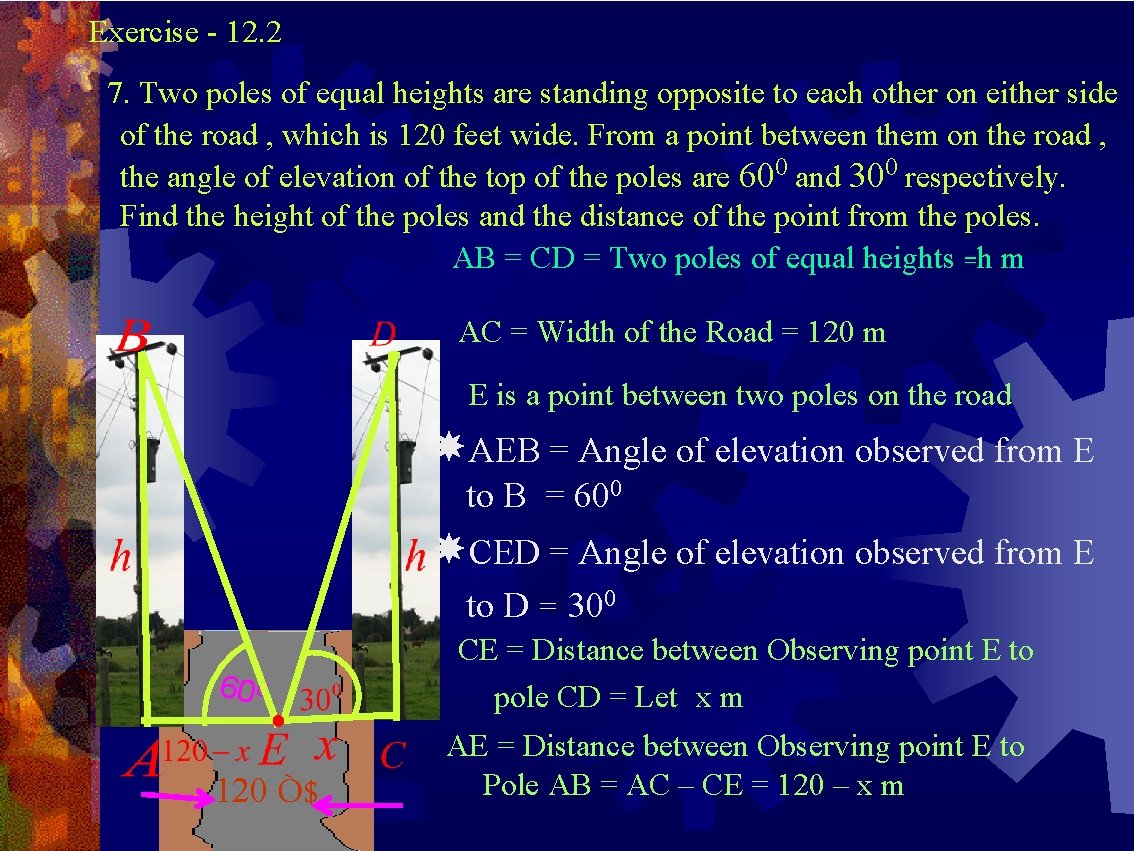
Exercise - 12. 2 7. Two poles of equal heights are standing opposite to each other on either side of the road , which is 120 feet wide. From a point between them on the road , the angle of elevation of the top of the poles are 600 and 300 respectively. Find the height of the poles and the distance of the point from the poles. AB = CD = Two poles of equal heights =h m AC = Width of the Road = 120 m E is a point between two poles on the road AEB = Angle of elevation observed from E to B = 600 CED = Angle of elevation observed from E to D = 300 60 0 120 Ò$. CE = Distance between Observing point E to pole CD = Let x m AE = Distance between Observing point E to Pole AB = AC – CE = 120 – x m

In ΔCDE, Opposite side to E is CD = h , Adjacent side to E is EC = x , hypotenuse ED In ΔADE, Opposite to E is AB = h , Adjacent side to E is EC = 120 – x , hypotenuse to EB AB = CD = Two poles of equal heights = 51. 96 m CE = Distance between Observing point E to pole CD = 90 m

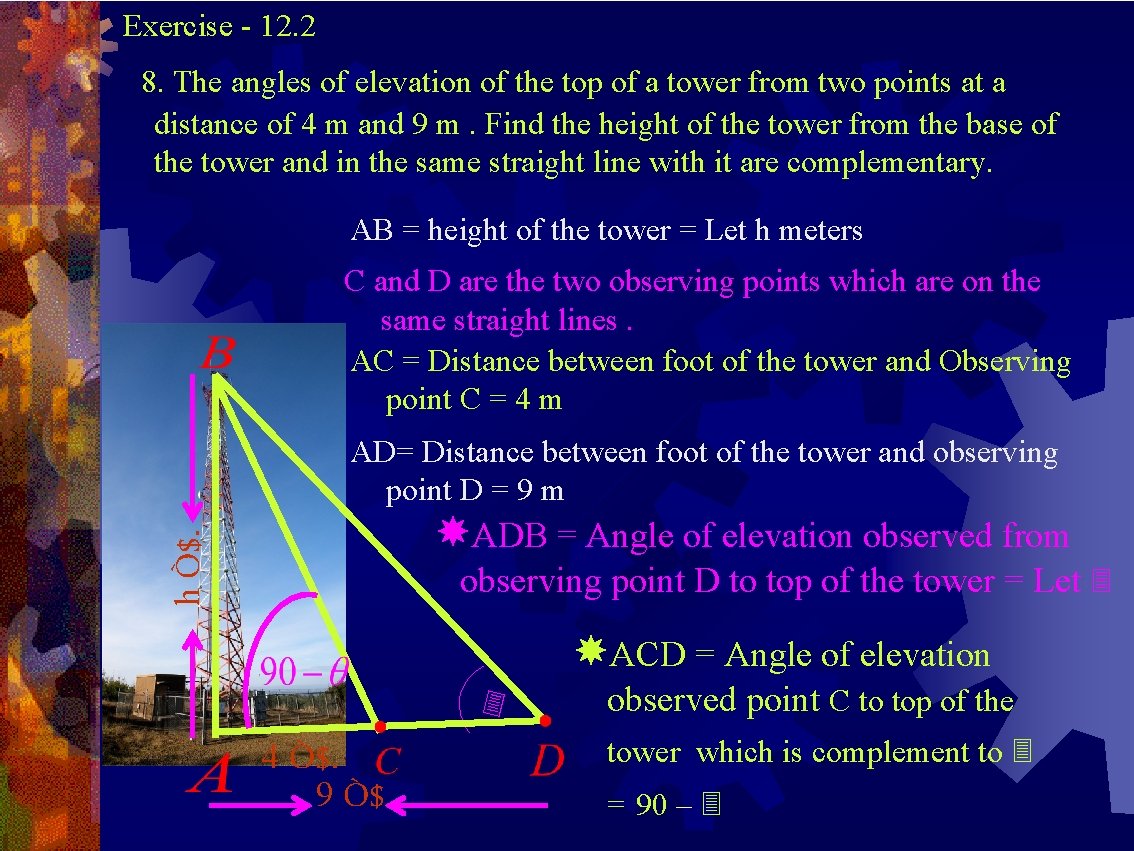
Exercise - 12. 2 8. The angles of elevation of the top of a tower from two points at a distance of 4 m and 9 m. Find the height of the tower from the base of the tower and in the same straight line with it are complementary. AB = height of the tower = Let h meters C and D are the two observing points which are on the same straight lines. AC = Distance between foot of the tower and Observing point C = 4 m AD= Distance between foot of the tower and observing point D = 9 m h Ò$. ADB = Angle of elevation observed from observing point D to top of the tower = Let ACD = Angle of elevation 4 Ò$. 9 Ò$. observed point C to top of the tower which is complement to = 90 –

In ΔABD, Opposite to D is AB = h, Adjacent side to D is AD = 9, hypotenuse is BD . . Comparing and ………. In ΔABC, Opposite side to C is AB = h, Adjacent to side to AC = 4, hypotenuse is BC AB = height of the tower = 6 m

9. The angle of elevation of a jet plane from a point A on the 0. After a flight of 15 seconds, the angle of elevation ground is 60 Exercise - 12. 2 changes to 300. If the jet plane is flying at a constant height of meters, Find the speed of the jet plane. DAB= The angle of elevation of a jet plane observed from a Point A on the ground = 600 DAC = After flight of 15 seconds, the angle of elevation observed from point A on the ground = 300 BD =CE = Constant height of the jet plane flying from the ground = Ò$. DE = BC = Within 15 Seconds , distance travelled by jet plane = Let x AD = Distance between observing point A to Perpendicular line of jet plane D = Let y

In ΔADB, Opposite side to A is BD, Adjacent side to A is AD, hypotenuse is AB Speed of the jet plane = Distance / Time Speed of the jet plane = 200 meters / Second In ΔAEC, Opposite side to A is CE, Adjacent side DE = BC = Within 15 Seconds , distance travelled by jet plane = 3000 m to A is AE, hypotenuse is AC

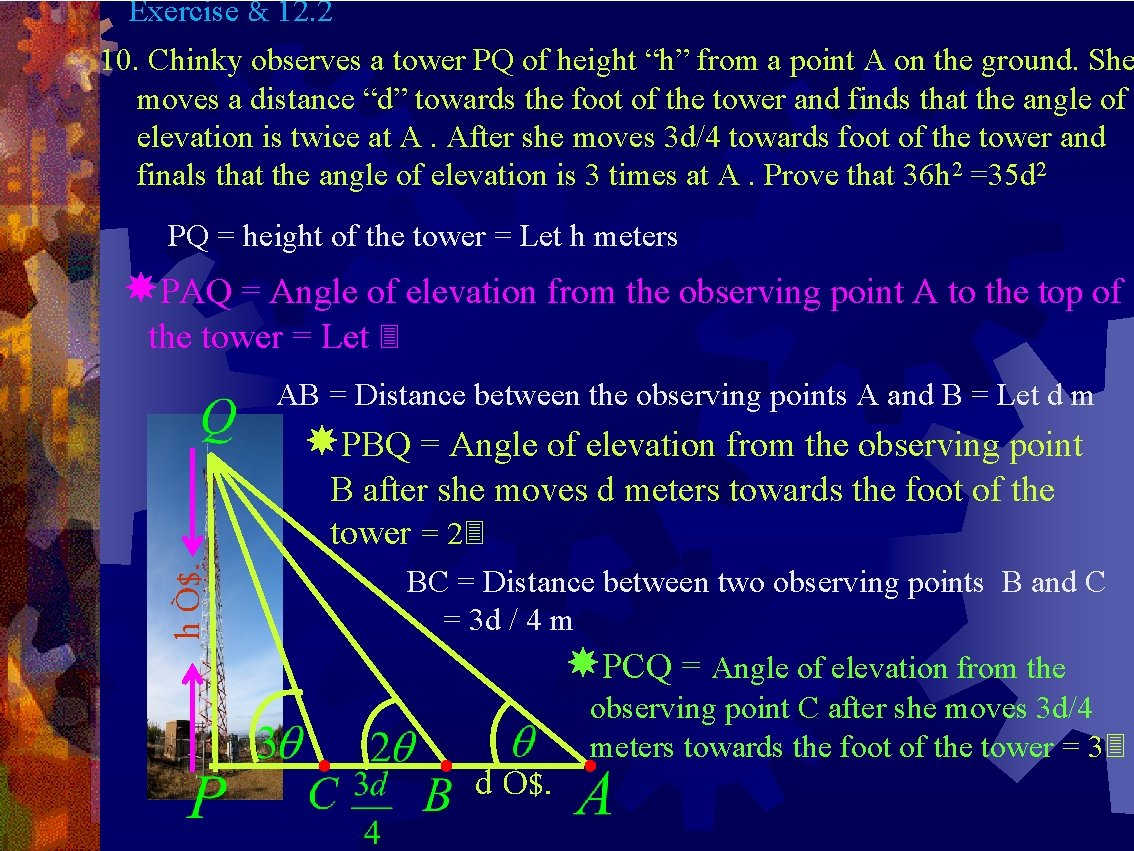
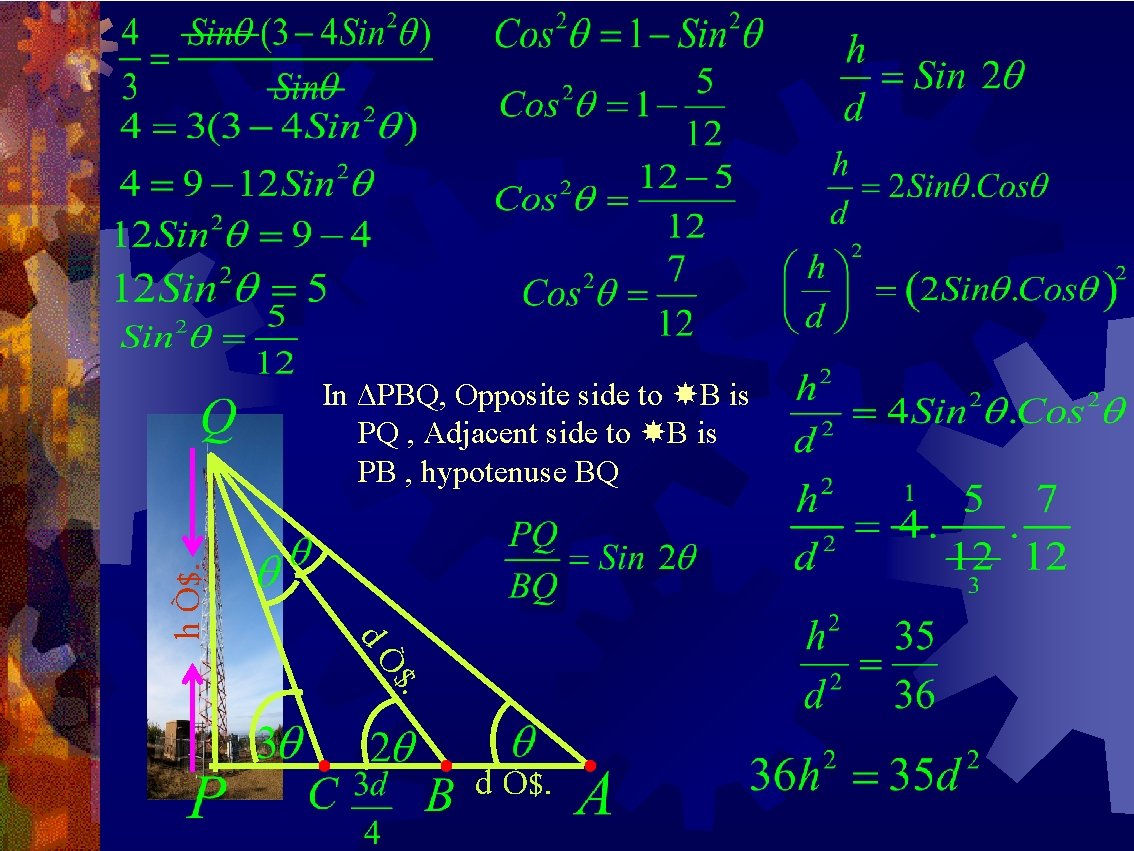
Exercise & 12. 2 10. Chinky observes a tower PQ of height “h” from a point A on the ground. She moves a distance “d” towards the foot of the tower and finds that the angle of elevation is twice at A. After she moves 3 d/4 towards foot of the tower and finals that the angle of elevation is 3 times at A. Prove that 36 h 2 =35 d 2 PQ = height of the tower = Let h meters PAQ = Angle of elevation from the observing point A to the top of the tower = Let AB = Distance between the observing points A and B = Let d m PBQ = Angle of elevation from the observing point h Ò$. B after she moves d meters towards the foot of the tower = 2 BC = Distance between two observing points B and C = 3 d / 4 m PCQ = Angle of elevation from the observing point C after she moves 3 d/4 meters towards the foot of the tower = 3 d Ò$.

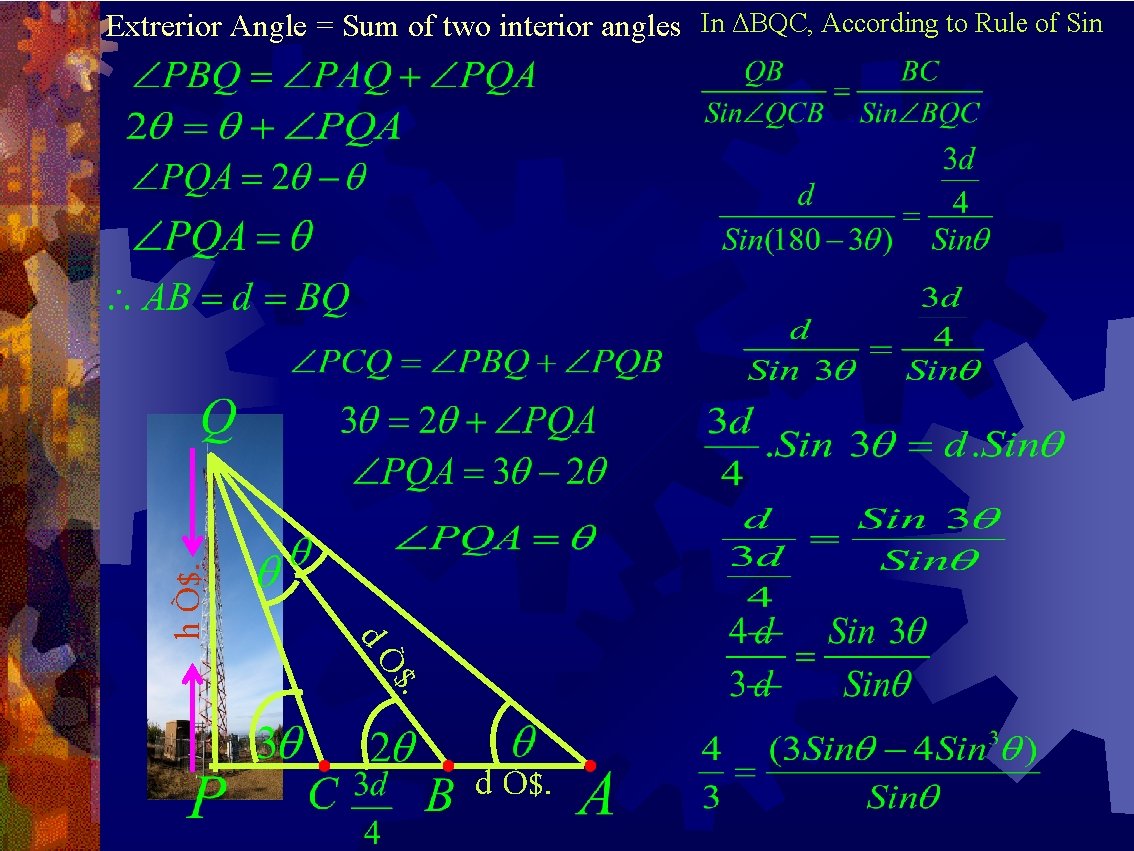
$. dÒ h Ò$. Extrerior Angle = Sum of two interior angles In ΔBQC, According to Rule of Sin d Ò$.

$. dÒ h Ò$. In ΔPBQ, Opposite side to B is PQ , Adjacent side to B is PB , hypotenuse BQ d Ò$.

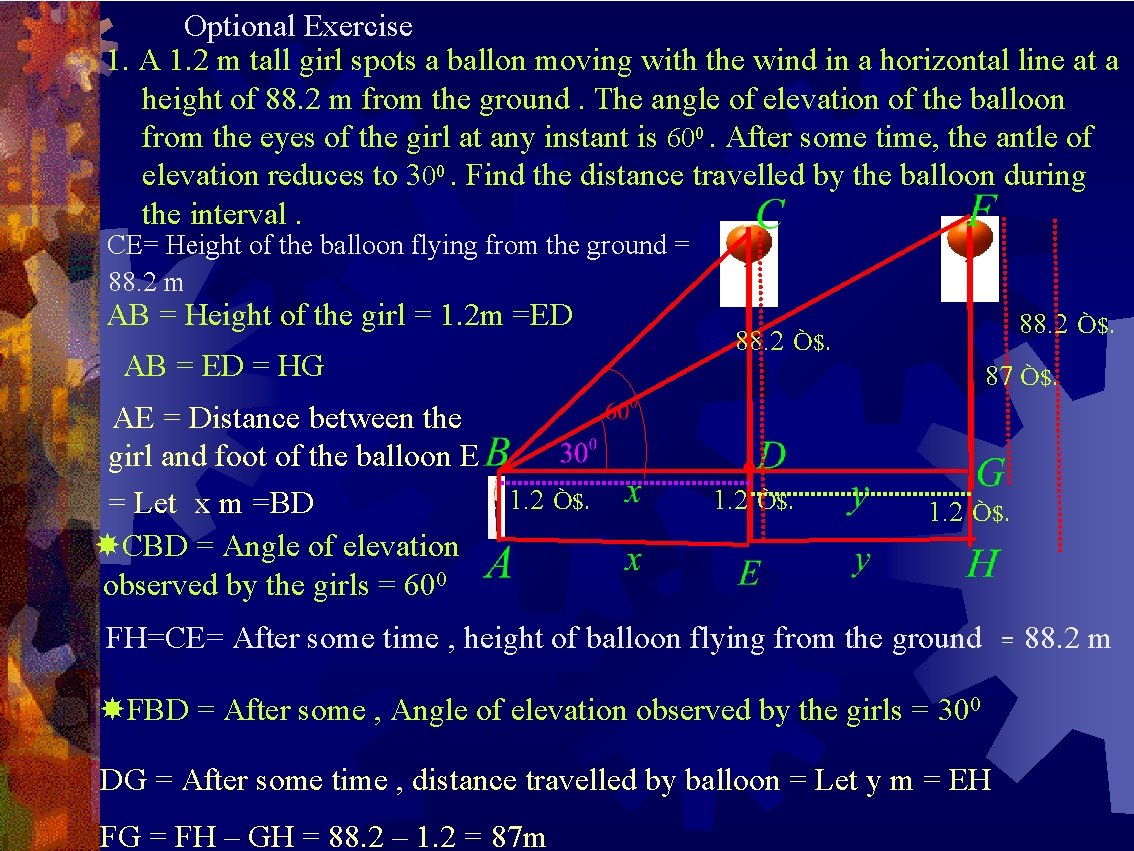
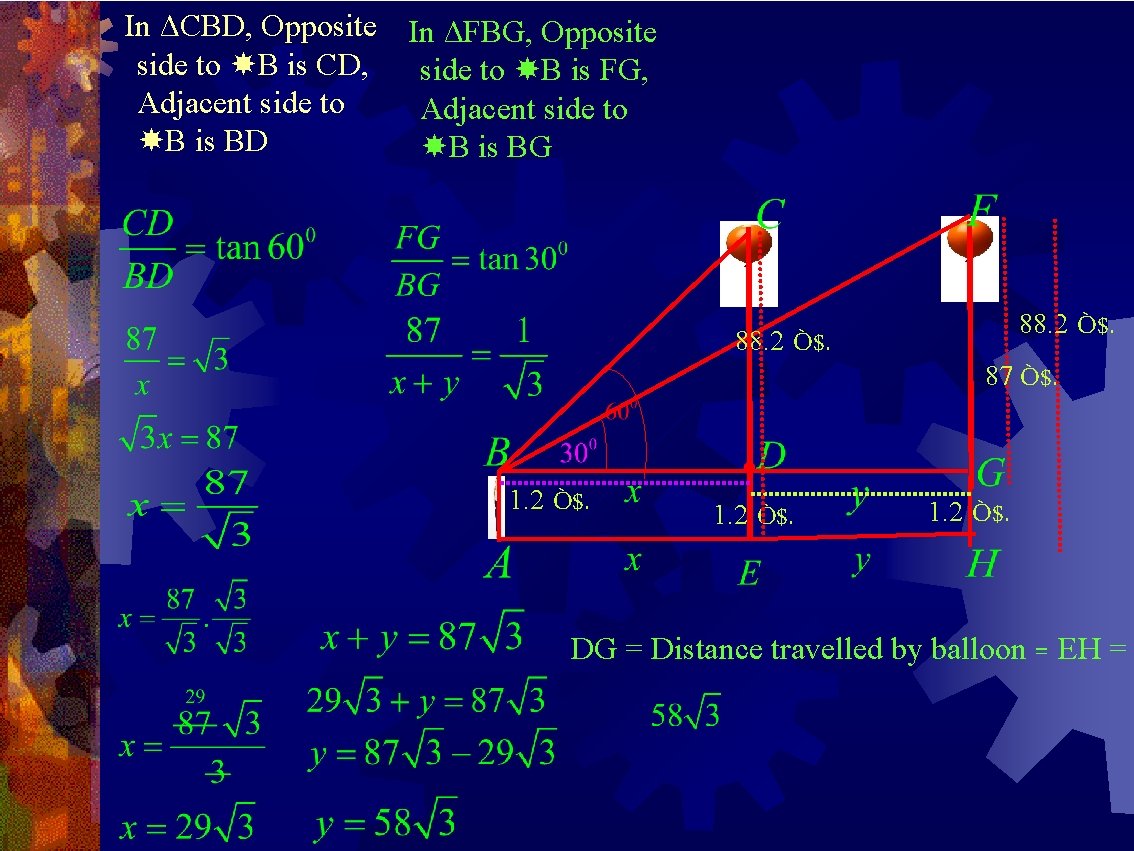
Optional Exercise 1. A 1. 2 m tall girl spots a ballon moving with the wind in a horizontal line at a height of 88. 2 m from the ground. The angle of elevation of the balloon from the eyes of the girl at any instant is 600. After some time, the antle of elevation reduces to 300. Find the distance travelled by the balloon during the interval. CE= Height of the balloon flying from the ground = 88. 2 m AB = Height of the girl = 1. 2 m =ED AB = ED = HG AE = Distance between the girl and foot of the balloon E 1. 2 Ò$. = Let x m =BD CBD = Angle of elevation observed by the girls = 600 88. 2 1. 2 88. 2 Ò$. 87 Ò$. 1. 2 Ò$. FH=CE= After some time , height of balloon flying from the ground FBD = After some , Angle of elevation observed by the girls = 300 DG = After some time , distance travelled by balloon = Let y m = EH FG = FH – GH = 88. 2 – 1. 2 = 87 m Ò$. = 88. 2 m

In ΔCBD, Opposite In ΔFBG, Opposite side to B is CD, side to B is FG, Adjacent side to B is BD B is BG 88. 2 1. 2 Ò$. 1. 2 88. 2 Ò$. 87 Ò$. 1. 2 Ò$. DG = Distance travelled by balloon = EH =

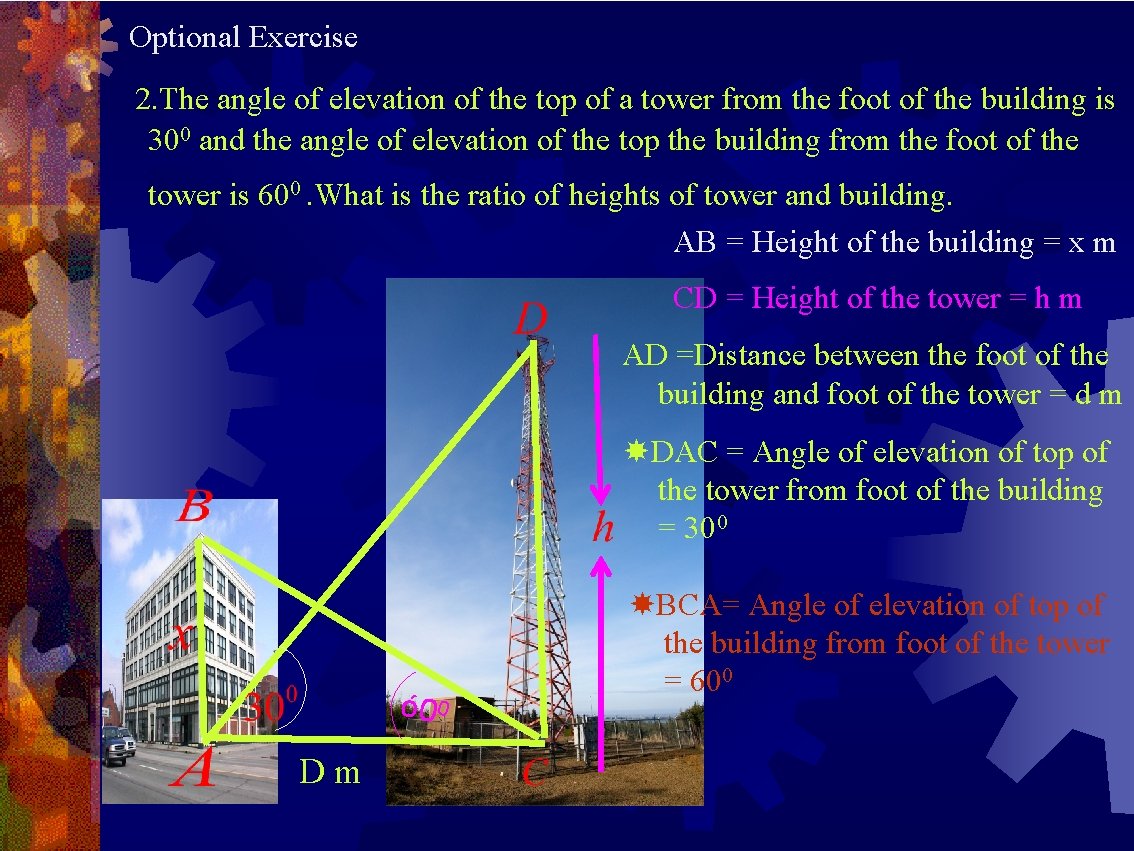
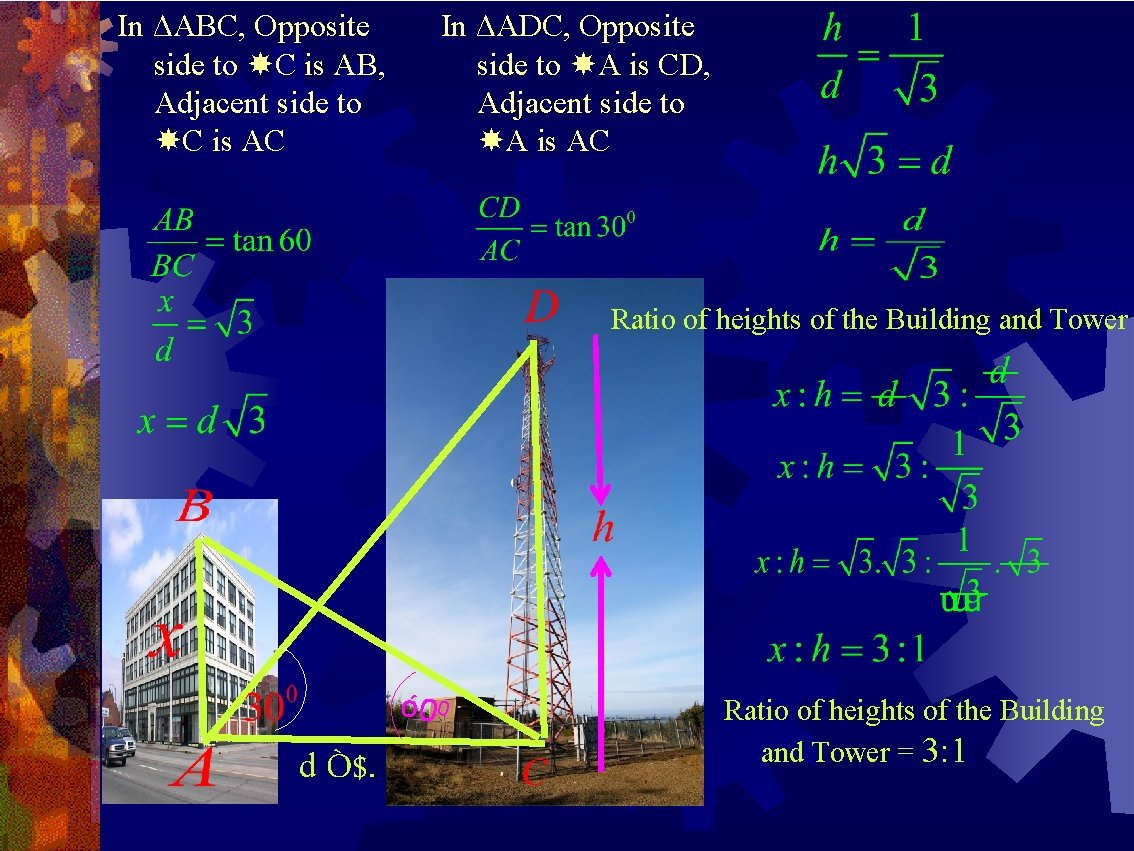
Optional Exercise 2. The angle of elevation of the top of a tower from the foot of the building is 300 and the angle of elevation of the top the building from the foot of the tower is 600. What is the ratio of heights of tower and building. AB = Height of the building = x m CD = Height of the tower = h m AD =Distance between the foot of the building and foot of the tower = d m DAC = Angle of elevation of top of the tower from foot of the building = 300 ó 0 0 Dm BCA= Angle of elevation of top of the building from foot of the tower = 600

In ΔABC, Opposite side to C is AB, Adjacent side to C is AC In ΔADC, Opposite side to A is CD, Adjacent side to A is AC Ratio of heights of the Building and Tower ó 0 0 d Ò$. Ratio of heights of the Building and Tower = 3: 1

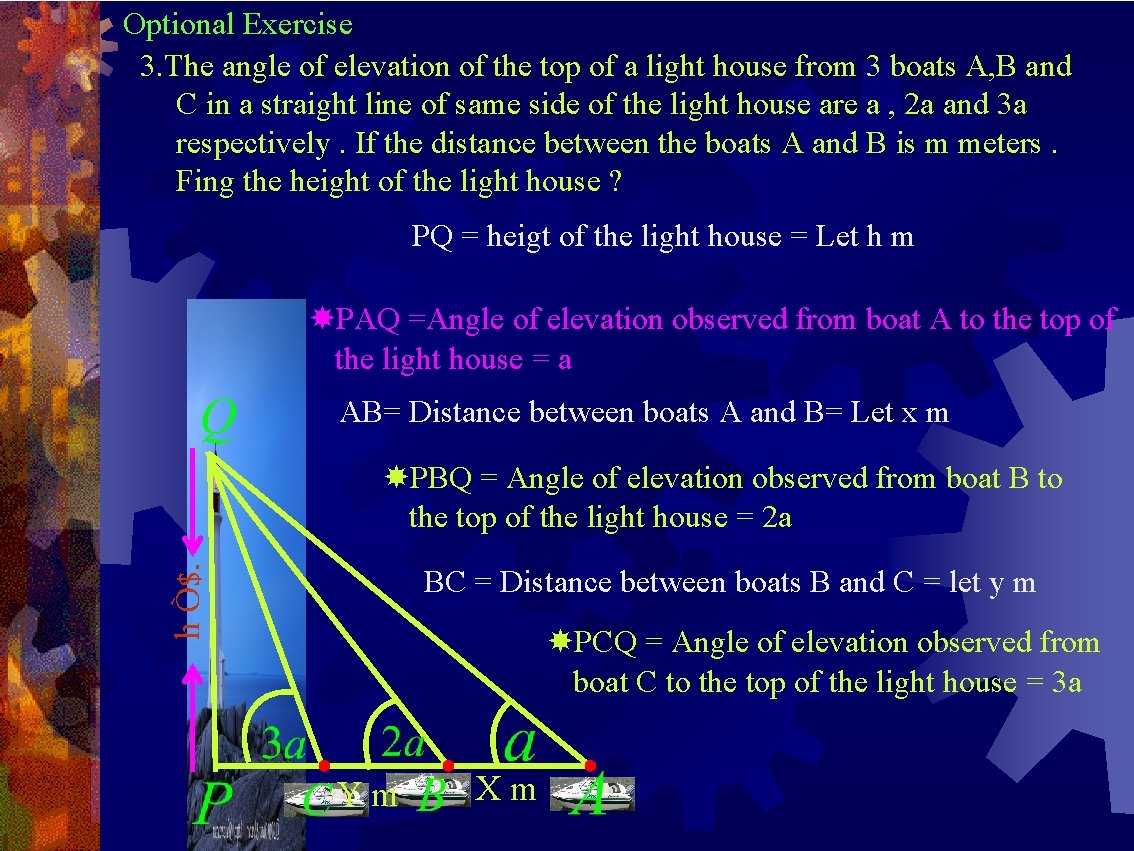
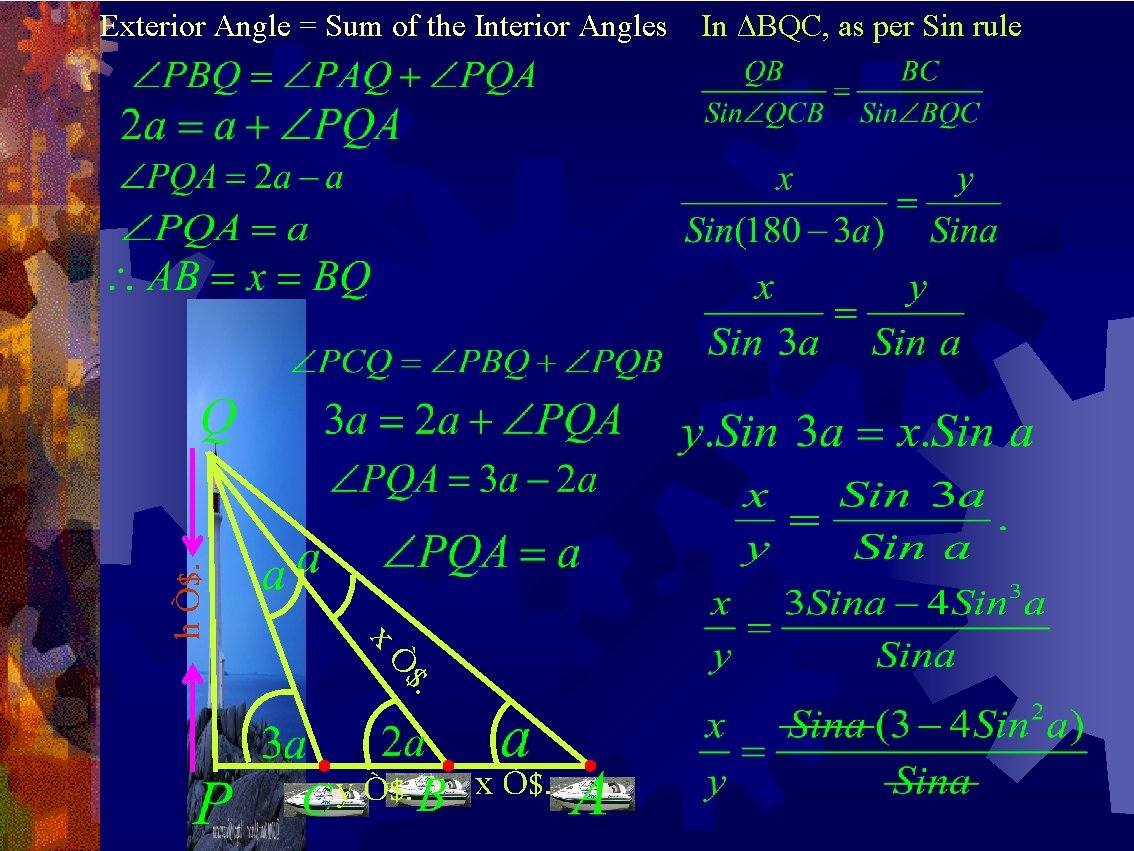
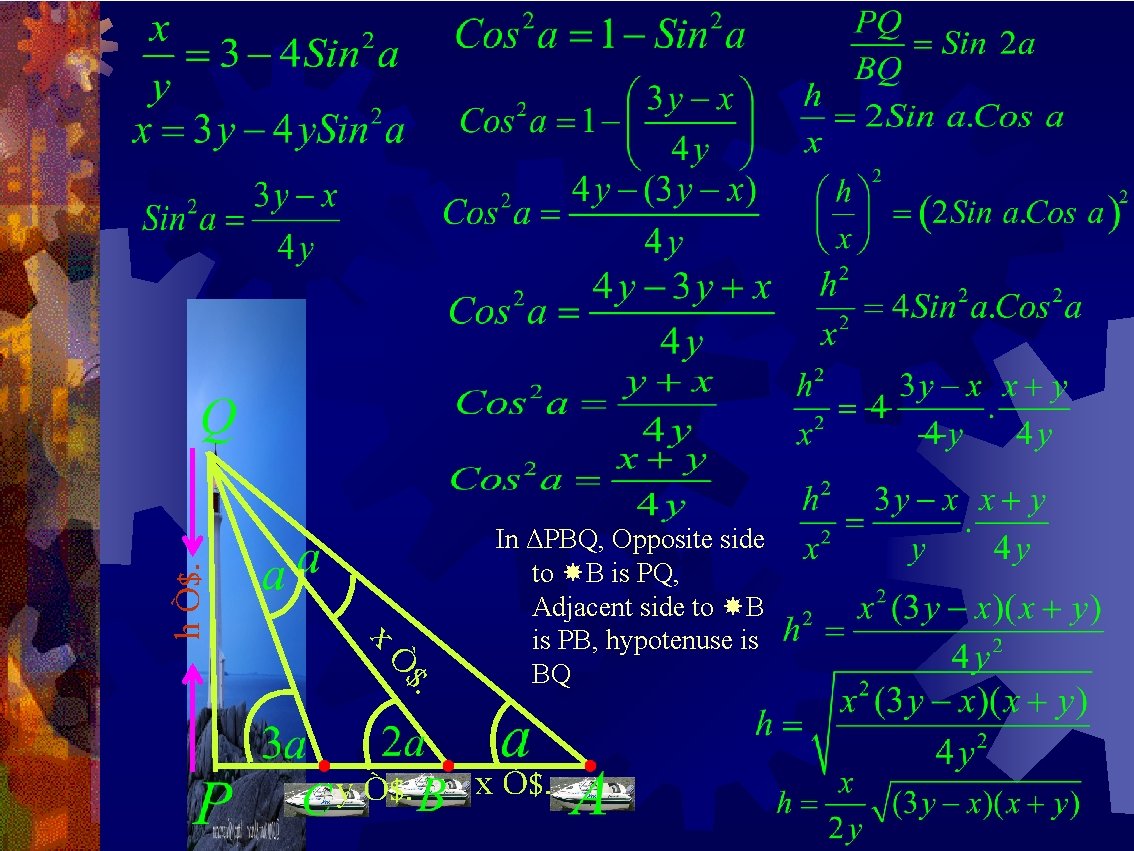
Optional Exercise 3. The angle of elevation of the top of a light house from 3 boats A, B and C in a straight line of same side of the light house are a , 2 a and 3 a respectively. If the distance between the boats A and B is m meters. Fing the height of the light house ? PQ = heigt of the light house = Let h m PAQ =Angle of elevation observed from boat A to the top of the light house = a AB= Distance between boats A and B= Let x m h Ò$. PBQ = Angle of elevation observed from boat B to the top of the light house = 2 a BC = Distance between boats B and C = let y m PCQ = Angle of elevation observed from boat C to the top of the light house = 3 a Ym Xm

$. xÒ h Ò$. Exterior Angle = Sum of the Interior Angles y Ò$. x Ò$. In ΔBQC, as per Sin rule

$. h Ò$. xÒ y Ò$. In ΔPBQ, Opposite side to B is PQ, Adjacent side to B is PB, hypotenuse is BQ x Ò$.

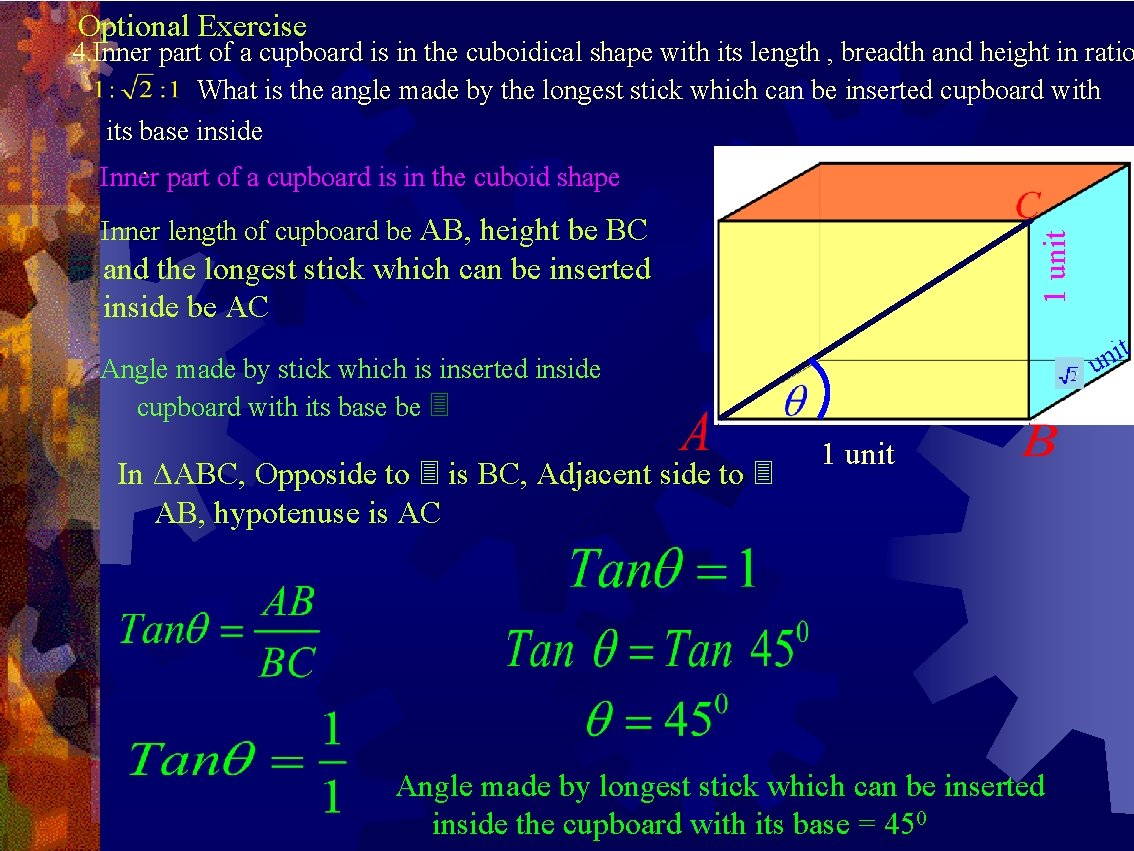
Optional Exercise 4. Inner part of a cupboard is in the cuboidical shape with its length , breadth and height in ratio What is the angle made by the longest stick which can be inserted cupboard with its base inside. part of a cupboard is in the cuboid shape Inner 1 unit Inner length of cupboard be AB, height be BC and the longest stick which can be inserted inside be AC it n u Angle made by stick which is inserted inside cupboard with its base be In ΔABC, Opposide to is BC, Adjacent side to AB, hypotenuse is AC 1 unit Angle made by longest stick which can be inserted inside the cupboard with its base = 450

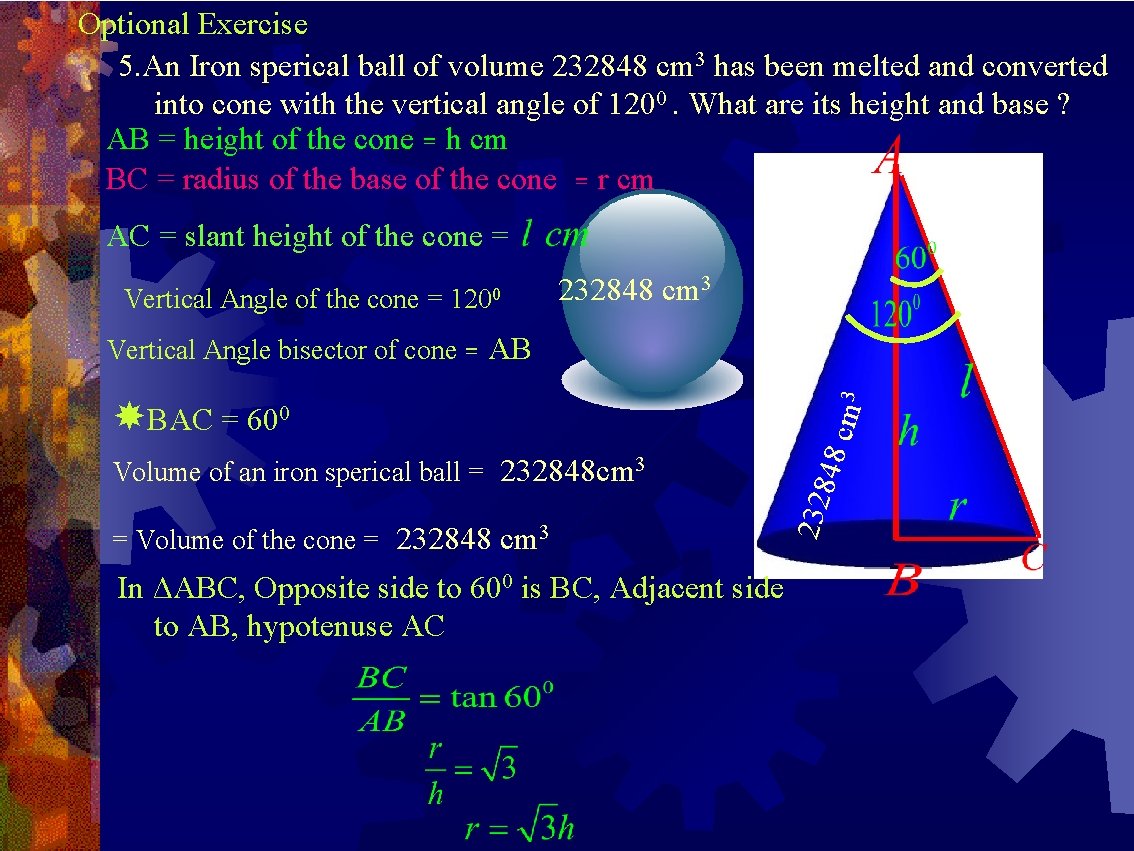
Optional Exercise 5. An Iron sperical ball of volume 232848 cm 3 has been melted and converted into cone with the vertical angle of 1200. What are its height and base ? AB = height of the cone = h cm BC = radius of the base of the cone = r cm AC = slant height of the cone = Vertical Angle of the cone = 1200 232848 cm 3 Volume of an iron sperical ball = 232848 cm 3 = Volume of the cone = 232848 cm 3 In ΔABC, Opposite side to 600 is BC, Adjacent side to AB, hypotenuse AC 2328 4 BAC = 600 8 cm 3 Vertical Angle bisector of cone = AB

Volume of the cone = 232848 cm 3 cm cm