11 th Edition TODAY AND TOMORROW Numbering System

11 th Edition TODAY AND TOMORROW Numbering System Chapter 7 Understanding Computers, 11 th Edition

The Decimal and Binary Numbering System n n Chapter 7 The decimal (base 10), numbering system uses 10 symbols—the digits 0, 1, 2, 3, 4, 5, 6, 7, 8, and 9—to represent all possible numbers and is the numbering system people use most often. The binary (base 2), numbering system is used extensively by computers to represent numbers and other characters. This system uses only two digits— 0 and 1. Understanding Computers, 11 th Edition 2

Representing Data - Decimal Numbers (Base 10) n Ø Ø We use Decimal numbers: n number based on 10 digits, 0, 1, 2, 3, …, 9 1 0 n 123 = (1 x 102) + (2 x 10 ) + (3 x 10 ) 2 1 0 n 764 =764(10)=7 x 10 + 6 x 10 + 4 x 10 n where in base 10, digits 0, 1, 2, … 7, 8, 9 are permissible (NOT 10). Note 100 = 1 In 764 the 7 is the most significant digit (MSD) and 4 is the least significant digit (LSD) Can use any Base n. Since digital work largely deals with two signals we select n=2 Binary uses the same principle Chapter 7 Understanding Computers, 11 th Edition 3

Decimal Numbers The position of each digit in a weighted number system is assigned a weight based on the base or radix of the system. The radix of decimal numbers is ten, because only ten symbols (0 through 9) are used to represent any number. The column weights of decimal numbers are powers of ten that increase from right to left beginning with 100 =1: … 105 104 103 102 101 100. For fractional decimal numbers, the column weights are negative powers of ten that decrease from left to right: 102 101 100. 10 -1 10 -2 10 -3 10 -4 … Chapter 7 Understanding Computers, 11 th Edition

Decimal Numbers Decimal numbers can be expressed as the sum of the products of each digit times the column value for that digit. Thus, the number 9240 can be expressed as (9 x 103) + (2 x 102) + (4 x 101) + (0 x 100) or 9 x 1, 000 + 2 x 100 + 4 x 10 + 0 x 1 Express the number 480. 52 as the sum of values of each digit. 480. 52 = (4 x 102) + (8 x 101) + (0 x 100) + (5 x 10 -1) +(2 x 10 -2) Chapter 7 Understanding Computers, 11 th Edition

Binary Numbers For digital systems, the binary number system is used. Binary has a radix of two and uses the digits 0 and 1 to represent quantities. The column weights of binary numbers are powers of two that increase from right to left beginning with 20 =1: … 25 24 23 22 21 20. For fractional binary numbers, the column weights are negative powers of two that decrease from left to right: 22 21 20. 2 -1 2 -2 2 -3 2 -4 … Chapter 7 Understanding Computers, 11 th Edition

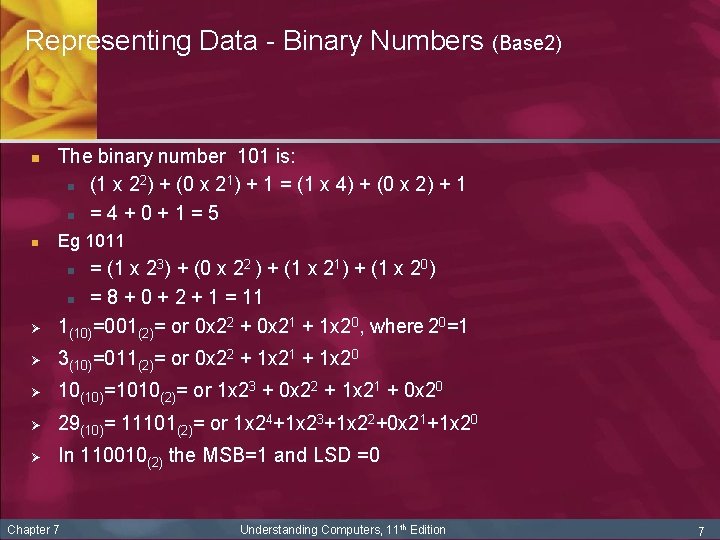
Representing Data - Binary Numbers (Base 2) n The binary number 101 is: 2 1 n (1 x 2 ) + (0 x 2 ) + 1 = (1 x 4) + (0 x 2) + 1 n = 4 + 0 + 1 = 5 n Eg 1011 Ø = (1 x 23) + (0 x 22 ) + (1 x 21) + (1 x 20) n = 8 + 0 + 2 + 1 = 11 1(10)=001(2)= or 0 x 22 + 0 x 21 + 1 x 20, where 20=1 Ø 3(10)=011(2)= or 0 x 22 + 1 x 21 + 1 x 20 Ø 10(10)=1010(2)= or 1 x 23 + 0 x 22 + 1 x 21 + 0 x 20 Ø 29(10)= 11101(2)= or 1 x 24+1 x 23+1 x 22+0 x 21+1 x 20 Ø In 110010(2) the MSB=1 and LSD =0 n Chapter 7 Understanding Computers, 11 th Edition 7

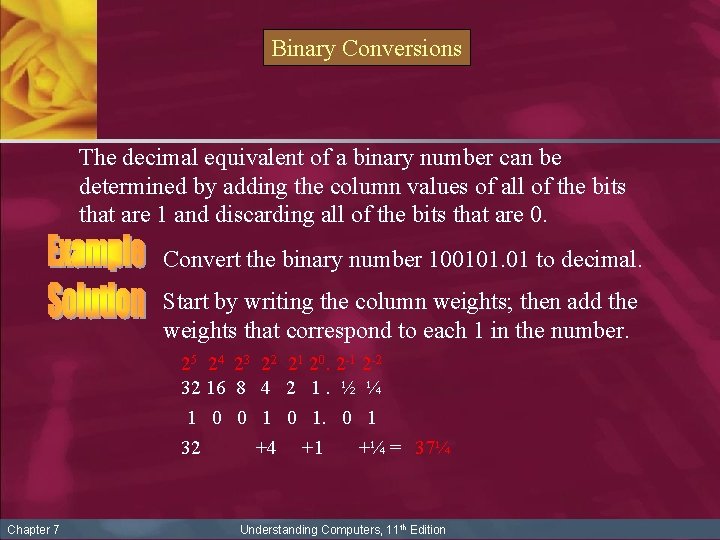
Binary Conversions The decimal equivalent of a binary number can be determined by adding the column values of all of the bits that are 1 and discarding all of the bits that are 0. Convert the binary number 100101. 01 to decimal. Start by writing the column weights; then add the weights that correspond to each 1 in the number. 25 24 23 22 21 20. 2 -1 2 -2 32 16 8 4 2 1. ½ ¼ 1 0 0 1 32 +4 +1 +¼ = 37¼ Chapter 7 Understanding Computers, 11 th Edition

Binary Conversions You can convert a decimal whole number to binary by reversing the procedure. Write the decimal weight of each column and place 1’s in the columns that sum to the decimal number. Convert the decimal number 49 to binary. The column weights double in each position to the right. Write down column weights until the last number is larger than the one you want to convert. 26 25 24 23 22 21 20. 64 32 16 8 4 2 1. 0 1 1 0 0 0 1. Chapter 7 Understanding Computers, 11 th Edition

Binary Conversions You can convert decimal to any other base by repeatedly dividing by the base. For binary, repeatedly divide by 2: Convert the decimal number 49 to binary by repeatedly dividing by 2. You can do this by “reverse division” and the answer will read from left to right. Put quotients to the left and remainders on top. 1 1 0 0 0 1 remainder 0 1 3 6 12 24 49 2 Answer: Continue until the last quotient is 0 Chapter 7 Quotient Decimal number base Understanding Computers, 11 th Edition

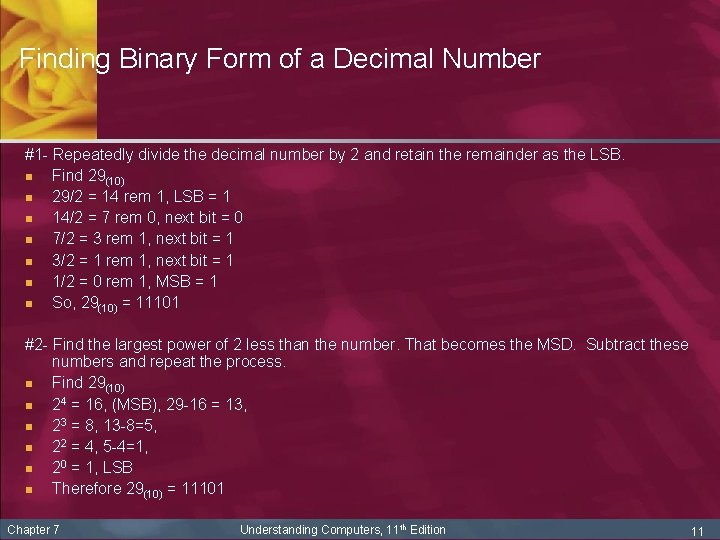
Finding Binary Form of a Decimal Number #1 - Repeatedly divide the decimal number by 2 and retain the remainder as the LSB. n Find 29(10) n 29/2 = 14 rem 1, LSB = 1 n 14/2 = 7 rem 0, next bit = 0 n 7/2 = 3 rem 1, next bit = 1 n 3/2 = 1 rem 1, next bit = 1 n 1/2 = 0 rem 1, MSB = 1 n So, 29(10) = 11101 #2 - Find the largest power of 2 less than the number. That becomes the MSD. Subtract these numbers and repeat the process. n Find 29(10) n 24 = 16, (MSB), 29 -16 = 13, n 23 = 8, 13 -8=5, n 22 = 4, 5 -4=1, n 20 = 1, LSB n Therefore 29(10) = 11101 Chapter 7 Understanding Computers, 11 th Edition 11

Base n n n n Chapter 7 Binary – 2 Octal – 8 Decimal – 10 Hexadecimal – 16 When dealing with collection of bits like binary words representing text characters using the ASCII (American Standard Code for Information Interchange) code – it is inconvenient to deal with each individual bit So may use octal (3 bit) words or hexadecimal (4 bit) words Understanding Computers, 11 th Edition 12

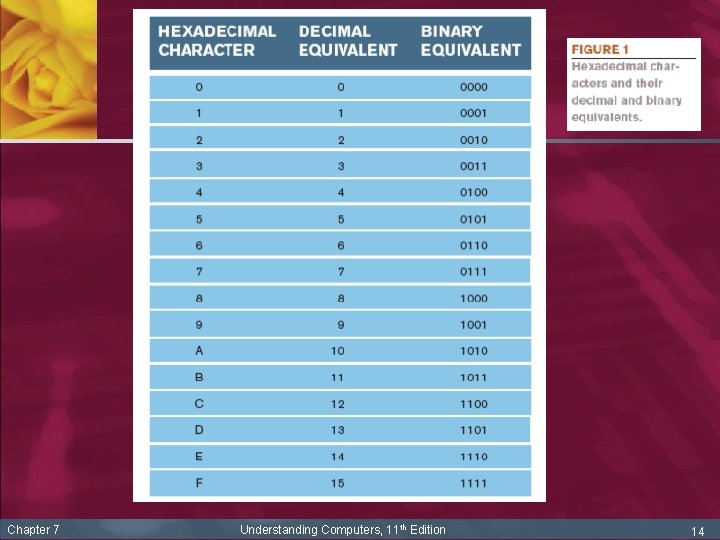
The Hexadecimal Numbering System n n The hexadecimal numbering system is also called the base 16 numbering system because it uses 16 different symbols. Hexadecimal is not itself a code that the computer uses to perform computations or to communicate with other machines. As you can see in Figure 1, each hex character has a 4 -bit binary counterpart, so any combination of 8 bits can be represented by exactly two hexadecimal characters. For example, the letter N (represented in ASCII by 01001110) has a hex representation of 4 E (see the Binary Equivalent column in Figure 1). Chapter 7 Understanding Computers, 11 th Edition 13

Chapter 7 Understanding Computers, 11 th Edition 14

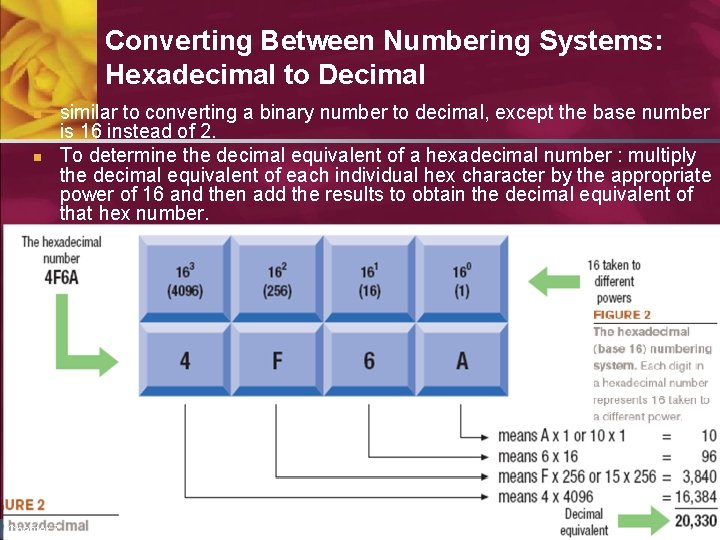
Converting Between Numbering Systems: Hexadecimal to Decimal n n similar to converting a binary number to decimal, except the base number is 16 instead of 2. To determine the decimal equivalent of a hexadecimal number : multiply the decimal equivalent of each individual hex character by the appropriate power of 16 and then add the results to obtain the decimal equivalent of that hex number. Chapter 7 Understanding Computers, 11 th Edition 15

Hexadecimal - Base 16 n n n Chapter 7 Base 16, using first 16 numerals including 6 letters: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F Because 16 is a power of 2, can use octal numbers to represent a group of 4 bits Example: 001111102 = 21 + 22 + 23 + 24 + 25 = 2 + 4 + 8 + 16 + 32 = 62 10 3 E 16 = 3 x 16 + 14 = 6210 Understanding Computers, 11 th Edition 16

Summary Decimal Hexadecimal Binary Hexadecimal Numbers Hexadecimal uses sixteen characters to represent numbers: the numbers 0 through 9 and the alphabetic characters A through F. Large binary number can easily be converted to hexadecimal by grouping bits 4 at a time and writing the equivalent hexadecimal character. Express 1001 0110 0000 11102 in hexadecimal: Group the binary number by 4 -bits starting from the right. Thus, 960 E Chapter 7 Understanding Computers, 11 th Edition 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Summary Decimal Hexadecimal Binary Hexadecimal Numbers Hexadecimal is a weighted number system. The column weights are powers of 16, which increase from right to left. Column weights 16 16. {4096 256 16 1. 3 2 1 0 Express 1 A 2 F 16 in decimal. Start by writing the column weights: 4096 256 16 1 1 A 2 F 16 1(4096) + 10(256) +2(16) +15(1) = 670310 Chapter 7 Understanding Computers, 11 th Edition 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 0 1 2 3 4 5 6 7 8 9 A B C D E F 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Hexadecimal to Binary / Binary to Hexadecimal n n To convert from hexadecimal to binary, we convert each hexadecimal digit separately to 4 binary digits Example, to convert F 6 A 9 to binary, we get F 1111 n n n 6 A 9 0110 1001 or 111101101001 in binary representation. To convert from binary to hexadecimal, we go through the reverse process. If the number of digits in the binary number is not divisible by 4, we add leading zeros to the binary number to force an even division. F Example, to convert the binary number 1101101010011 to hexadecimal, we get 0001 1011 0101 0011 1 n n Chapter 7 B 5 3 or l. B 53 in hexadecimal representation. Note that three leading zeros were added to change the initial 1 to 0001 before making the conversion. Understanding Computers, 11 th Edition 19

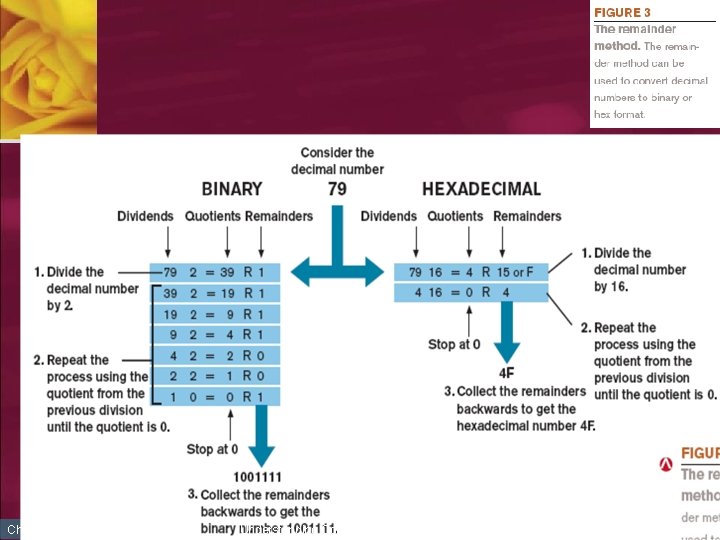
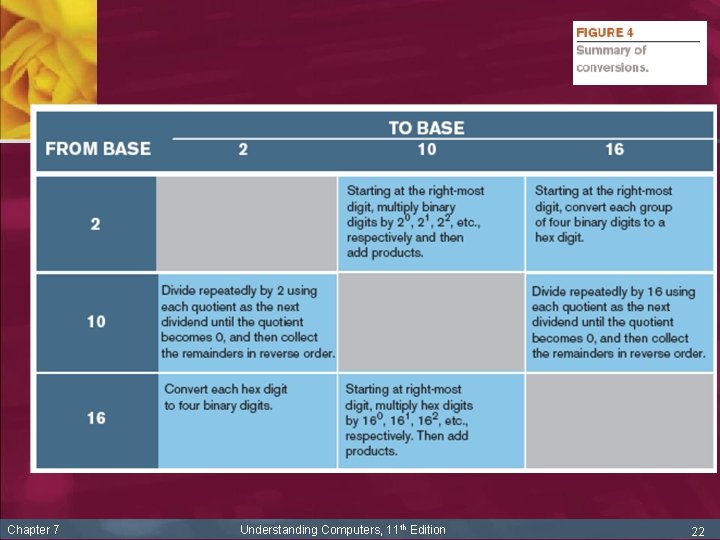
Decimal to Binary/Decimal to Hexadecimal n n n Chapter 7 Use the remainder method. The decimal number is divided by 2 (to convert to a binary number) or 16 (to convert to a hexadecimal number). The remainder of the division operation is recorded and the division process is repeated using the quotient as the next dividend, until the quotient becomes 0. At that point, the collective remainders (written backwards) represent the equivalent binary or hexadecimal number (see Figure 3). Understanding Computers, 11 th Edition 20

Chapter 7 Understanding Computers, 11 th Edition 21

Chapter 7 Understanding Computers, 11 th Edition 22

Octal - Base 8 n n n Chapter 7 Base 8, using first 8 numerals: 0, 1, 2, 3, 4, 5, 6, 7 Because 8 is a power of 2, can use octal numbers to represent a group of 3 bits Example: 1001112 = 1+2+4+32 = 3910 478 = 4 x 8 + 7 = 3910 Understanding Computers, 11 th Edition 23

Summary Decimal Octal Numbers Octal uses eight characters the numbers 0 through 7 to represent numbers. There is no 8 or 9 character in octal. Binary number can easily be converted to octal by grouping bits 3 at a time and writing the equivalent octal character for each group. Express 1 001 011 000 001 1102 in octal: Group the binary number by 3 -bits starting from the right. Thus, 1130168 Chapter 7 Understanding Computers, 11 th Edition 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Octal Binary 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Summary Decimal Octal Numbers Octal is also a weighted number system. The column weights are powers of 8, which increase from right to left. Column weights {5128 3 82 64 81 8 80. 1. Express 37028 in decimal. Start by writing the column weights: 512 64 8 1 3 7 0 28 3(512) + 7(64) +0(8) +2(1) = 198610 Chapter 7 Understanding Computers, 11 th Edition 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 Octal Binary 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 0000 0001 0010 0011 0100 0101 0110 0111 1000 1001 1010 1011 1100 1101 1110 1111

Computer Arithmetic n n Chapter 7 Note that with binary and hexadecimal, as in decimal arithmetic, you carryto and borrow from the column to the left as needed as you move from right to left. Instead of carrying or borrowing 10, however—as you would in the decimal system—you carry or borrow 2 (binary) or 16 (hexadecimal). Understanding Computers, 11 th Edition 26

1. For the binary number 1000, the weight of the column with the 1 is a. 4 b. 6 c. 8 d. 10 2. The hexadecimal number 2 C has a decimal equivalent value of a. 14 b. 44 c. 64 d. none of the above Chapter 7 Understanding Computers, 11 th Edition © 2009 Pearson Education 27