11 Radiation 11 1 Dipole Radiation 11 1

11 Radiation 11. 1 Dipole Radiation 11. 1. 1 What is Radiation? 11. 1. 2 Electric Dipole Radiation. 11. 1. 3 Magnetic Dipole Radiation. 11. 1. 4 Radiation from an Arbitrary Source. 11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge. 11. 2. 2 Radiation Reaction. 11. 2. 3 The Physical Basis of the Radiation Reaction. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 1

11. 1 Dipole Radiation 11. 1. 1 What is Radiation? Radiation never comes back The source of all electromagnetic fields is some arrangement of electric charge. But a charge at rest does not generate electromagnetic waves nor does a steady current. It takes accelerating charges, and changing currents. Electromagnetic waves in vacuum propagate out "to infinity, " carrying energy with them; the signature of radiation is this irreversible flow of energy away from the source. Throughout this chapter we shall assume the source is localized near the origin. The power radiated is the limit of this quantity as r goes to infinity: This is the energy (per unit time) that is transported out to infinity, and never comes back. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 2

11. 1 Dipole Radiation 11. 1. 1 What is Radiation? �� and �� behavior of radiation source Static sources do not radiate Jefimenko's equations 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 3

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Approximations The oscillating electric dipole 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 4

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Potentials for an oscillating dipole 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 5

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Potentials for an oscillating dipole The potential of a stationary dipole 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 6

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Potentials for an oscillating dipole radiation zone The vector potential is determined by the current flowing in the wire 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 7

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Fields for an oscillating dipole 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 8

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation �� and �� behavior of radiation source 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 9

11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Average power The energy radiated by an oscillating electric dipole is The intensity is obtained by averaging (in time) over a complete cycle: There is no radiation along the axis of the dipole; the intensity profiles takes the form of a donut, with its maximum in the equatorial plane It is independent of the radius of the sphere, as one would expect from conservation of energy. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 10

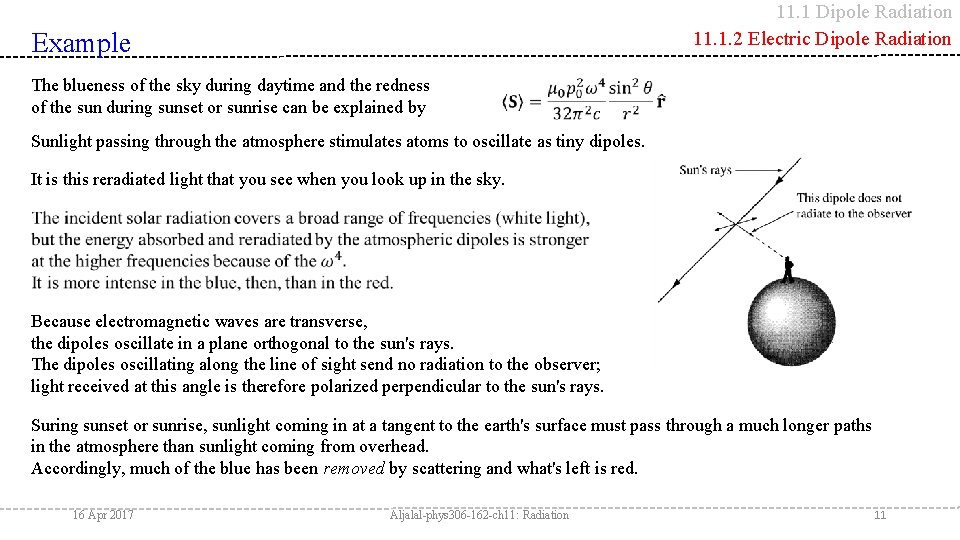
11. 1 Dipole Radiation 11. 1. 2 Electric Dipole Radiation Example The blueness of the sky during daytime and the redness of the sun during sunset or sunrise can be explained by Sunlight passing through the atmosphere stimulates atoms to oscillate as tiny dipoles. It is this reradiated light that you see when you look up in the sky. Because electromagnetic waves are transverse, the dipoles oscillate in a plane orthogonal to the sun's rays. The dipoles oscillating along the line of sight send no radiation to the observer; light received at this angle is therefore polarized perpendicular to the sun's rays. Suring sunset or sunrise, sunlight coming in at a tangent to the earth's surface must pass through a much longer paths in the atmosphere than sunlight coming from overhead. Accordingly, much of the blue has been removed by scattering and what's left is red. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 11

11. 1 Dipole Radiation 11. 1. 3 Magnetic Dipole Radiation Vector potential An alternating current in a wire loop of radius b The oscillating magnetic dipole moment, The loop is uncharged, so the scalar potential is zero. The retarded vector potential is 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 12

11. 1 Dipole Radiation 11. 1. 3 Magnetic Dipole Radiation Vector potential drop the second-order term. This term integrates to zero. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 13

11. 1 Dipole Radiation 11. 1. 3 Magnetic Dipole Radiation Electric field The vector potential of an oscillating perfect magnetic dipole The potential of a magnetic dipole 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 14

11. 1 Dipole Radiation 11. 1. 3 Magnetic Dipole Radiation Magnetic field The energy flux for magnetic dipole radiation is The intensity is The total radiated power 16 Apr 2017 The intensity profile has the shape of a donut as in the case of electric dipole. Aljalal-phys 306 -162 -ch 11: Radiation 15

11. 1 Dipole Radiation 11. 1. 3 Magnetic Dipole Radiation Comparison Electric dipole Magnetic dipole For configurations with comparable dimensions, the power radiated electrically is enormously greater. Let One should expect electric dipole radiation to dominate. Only when the system configuration excludes any electric contribution, will the magnetic dipole radiation reveal itself. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 16

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Scalar potential An arbitrary configuration of charge and current is localized within some finite volume near the origin. The retarded scalar potential is The dot is differentiation with respect to time. Approximation 2: Drop the second-order term 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 17

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Scalar potential In the static case, these terms are the monopole and dipole contributions to the multipole expansion for V We will show that these terms will not contribute to the radiating fields. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 18

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Vector potential The vector potential is Drop the second-order term, We will show that this term will contribute to the radiating fields. Ignore. See next slide. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 19

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Proof The continuity equation The x-component The divergence theorem The y and z components 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 20

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Electric field 3 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 21

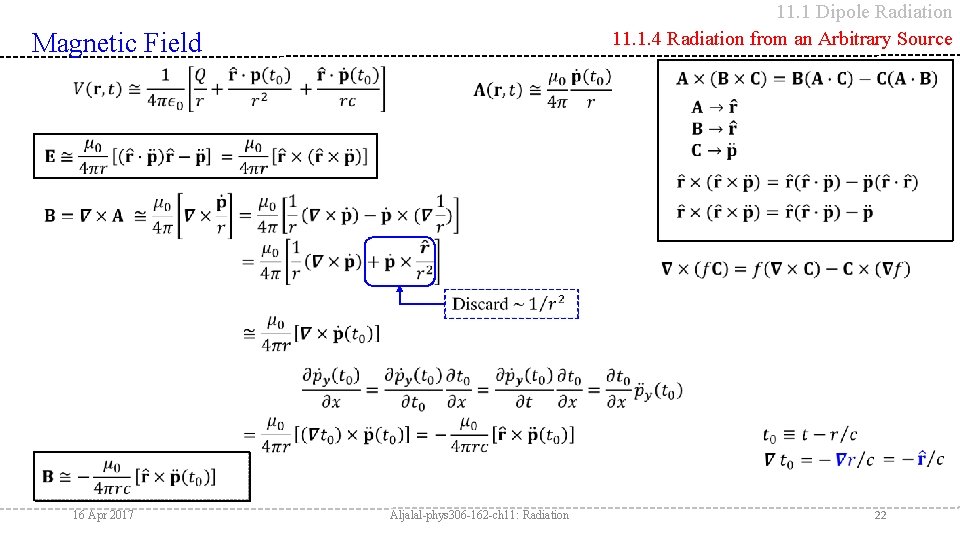
11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Magnetic Field 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 22

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Fields in spherical coordinates The Poynting vector is The total radiated power is 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 23

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Example For an oscillating electric dipole The same as before. The power radiated for a single point charge is This is Larmor formula 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation We'll derive it again by different means. 24

11. 1 Dipole Radiation 11. 1. 4 Radiation from an Arbitrary Source Multipole expansion Because charge is conserved, an electric monopole does not radiate In the acoustical analog monopoles do radiate. . . . and so it goes. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 25

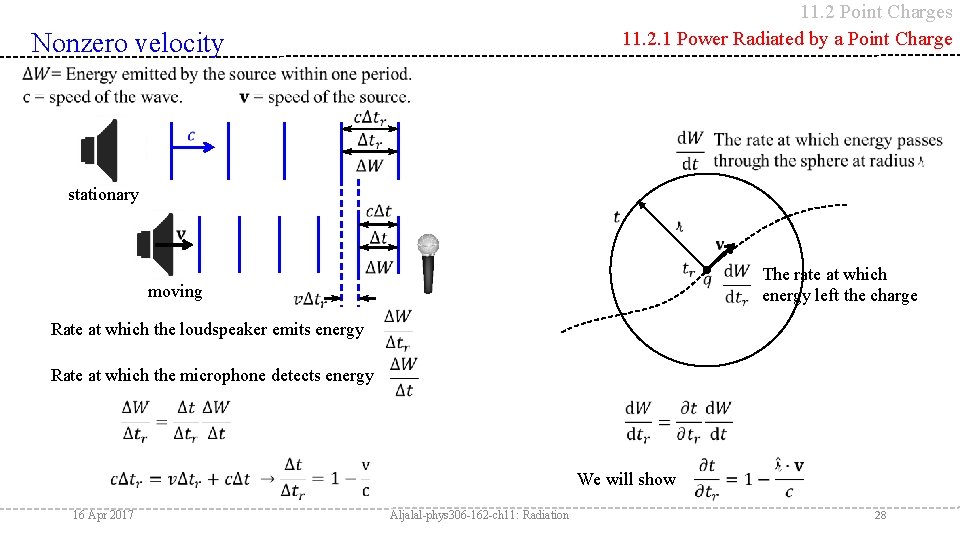
11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Radiation field The fields of a point charge q in arbitrary motion The 1 st term is the velocity field The 2 nd term is the acceleration (or radiation) field The Poynting vector is Some of this energy flux is just field energy carried along by the particle as it moves. The radiated energy is the stuff that detaches itself from the charge and propagates off to infinity. for the radiation to reach the sphere, and at that moment integrate the Poynting vector over the surface. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 26

11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Instantaneous zero velocity No power is radiated in the forward or backward direction. It is emitted in a donut about the direction of instantaneous acceleration. The total power radiated is 16 Apr 2017 The Larmor formula Aljalal-phys 306 -162 -ch 11: Radiation 27

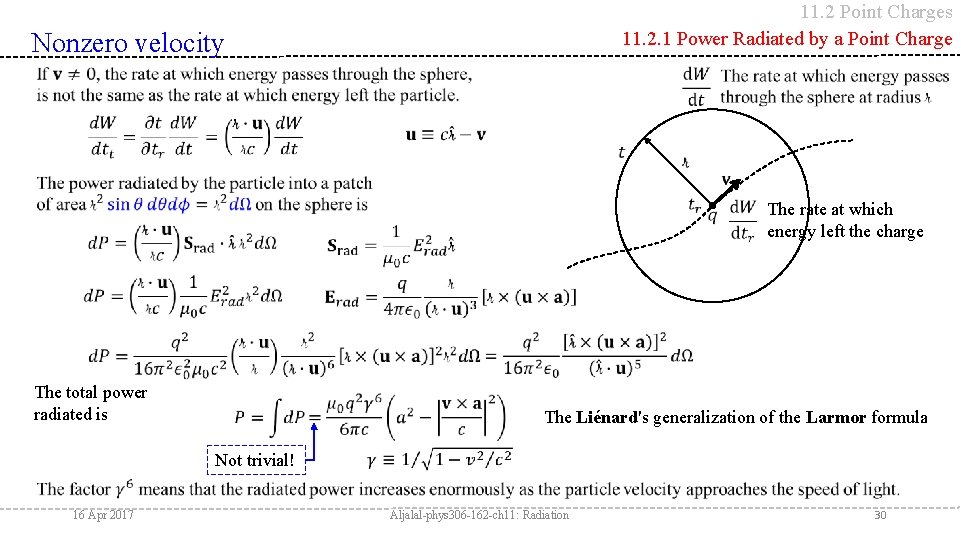
11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Nonzero velocity stationary moving Rate at which the loudspeaker emits energy The rate at which energy left the charge Rate at which the microphone detects energy 16 Apr 2017 We will show Aljalal-phys 306 -162 -ch 11: Radiation 28

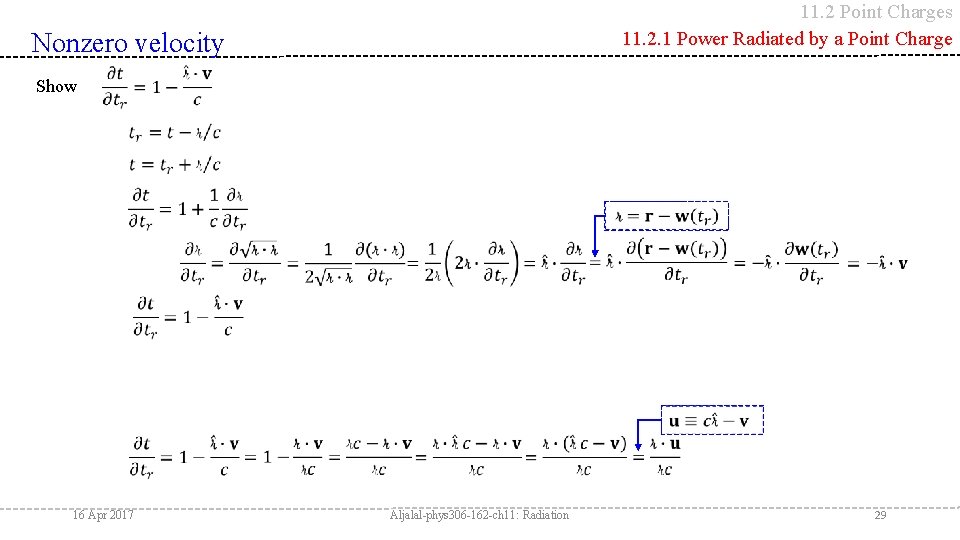
11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Nonzero velocity Show 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 29

11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Nonzero velocity The rate at which energy left the charge The total power radiated is Not trivial! The Liénard's generalization of the Larmor formula 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 30

11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Example 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 31

11. 2 Point Charges 11. 2. 1 Power Radiated by a Point Charge Example This result is consistent with the Liénard formula 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 32

11. 2 Point Charges 11. 2. 2 Radiation Reaction Exchange energy An accelerating charge radiates. This radiation carries off energy, which must come at the expense of the particle's kinetic energy. Under the influence of a given force, therefore, a charged particle accelerates less than a neutral one of the same mass. This equation is wrong because we ignore the energy exchange with the velocity fields. As the particle accelerates and decelerates energy is exchanged between it and the velocity fields, at the same time as energy is irretrievably radiated away by the acceleration fields. If we want to know the recoil force exerted by the fields on the charge, we need to consider the total power lost at any instant, not just the portion that eventually escapes in the form of radiation. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 33

11. 2 Point Charges 11. 2. 2 Radiation Reaction Abraham-Lorentz formula The energy lost by the particle in any given time interval, then, must equal the energy carried away by the radiation plus whatever extra energy has been pumped into the velocity fields. If we consider only intervals over which the system returns to its initial state, then the energy in the velocity fields is the same at both ends, and the only net loss is in the form of radiation. The Abraham-Lorentz formula for the radiation reaction force 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 34

11. 2 Point Charges 11. 2. 2 Radiation Reaction Example The equation of motion is 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 35

Self-force 11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction The Abraham-Lorentz formula for the radiation reaction was derived using conservation of energy. The force must be a recoil effect of the particle's own fields acting back on the charge. The fields of a point charge blow up right at the particle, so it's hard to calculate the force they exert. We avoid this problem by considering an extended charge distribution, for which the field is finite everywhere; at the end, we'll take the limit as the size of the charge goes to zero. If the distribution is divided up into infinitesimal chunks, and the imbalances are added up for all such pairs, the result is a net force of the charge on itself. It is this self-force, resulting from the breakdown of Newton's third law within the structure of the particle, that accounts for the radiation reaction. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 36

11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction Simple model 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 37

11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction Simple model So the net force on the dumbbell is Expand in powers of d. The dumbbell instantaneously at rest at the retarded time. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 38

11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction Simple model Use this as an approximation for the cubic term, And so on 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 39

11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction Simple model 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 40

11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction Simple model Newton’s second law The first term adds to the dumbbell's mass. In effect, the total inertia of the charged dumbbell is The potential energy of this configuration (in the static case) is 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 41

11. 2 Point Charges 11. 2. 3 The Physical Basis of the Radiation Reaction Simple model The second term is the radiation reaction. It differs from the Abraham-Lorentz formula by a factor of 2. This is only the self-force associated with the interaction between 1 and 2. There remains the force of each end on itself. When the latter is included the result is the same as the Abraham-Lorentz formula The radiation reaction is due to the force of the charge on itself. In other words, The net force exerted by the fields generated by different parts of the charge distribution acting on one another. 16 Apr 2017 Aljalal-phys 306 -162 -ch 11: Radiation 42