11 Mathematics Advanced FUNCTIONS F 1 2 INTRODUCTION

11 Mathematics Advanced FUNCTIONS F 1. 2 INTRODUCTION TO FUNCTIONS ALLPPT. com _ Free Power. Point Templates, Diagrams and Charts

Basics… • Defining and using functions and relations • Using function notation, domain and range, independent and dependent variables • Graphing functions • One-to-one, one-to-many, many-to-one, and many-to-many functions • Determining if a relation is a function and one-to-one • Odd and even functions • Sum, difference, product and quotients of functions • Composite functions • Finding intercepts of functions

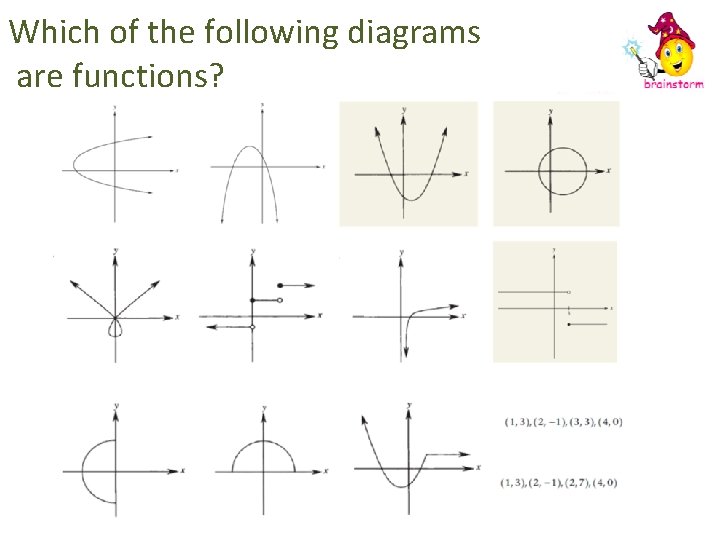
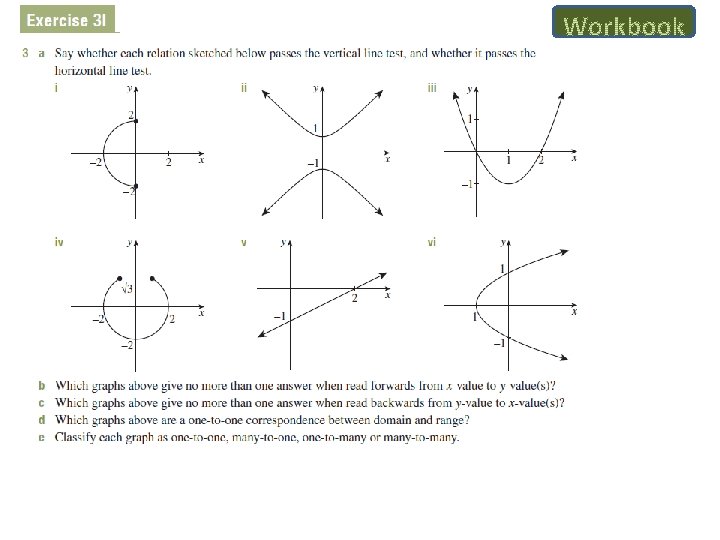
Function Definition A relation is a set of ordered points ( x , y ) where the variables x and y are related according to some rule. A function is a special type of relation. It is like a machine where for every INPUT there is only one OUTPUT. A function is a relationship between two variables where for every independent variable, there is only one dependent variable. This means that for every x value, there is only one y value. Which diagram below shows a function?

Function Notation We can assign the name f(x) to a function. We can now write the output of the function f(x) = 100+40 x as follows: f (0) = 100, f (1) = 140, f (2) = 180, f (3) = 220, . . . This is read aloud as ‘ f of zero is equal to one hundred’, and so on. We use f(x) instead of y. If f(x) = x 2 + 4, evaluate ) f(3) ) f(-2) c) f(a+b)

Graphing Functions The graph of a function consists of all the ordered pairs (x, y) plotted on a pair of axes, where x and y are the values of the input and output variables. No two points on the graph ever have the same x-coordinate. In most graphs in this course, the points join up to make a smooth curve. A function is a set of ordered pairs (x, y) in which no two ordered pairs have the same x-coordinate. Functions (but not relations in general) are also called maps or mappings. The word map may also be used as a verb. Thus in the function f (x) = 2 x, we may say that ‘ 3 is mapped to 8’. Domain and Range The domain of a function is the set of all possible x-coordinates. The range of a function is the set of all possible y-coordinates. It is usually easier to find the range after the graph has been drawn.

Natural Domain If no restriction is given, the domain is all x-values that can validly be substituted into the equation. This is called the natural domain. New notation in this course includes writing the domain this way:

Which of the following diagrams are functions?

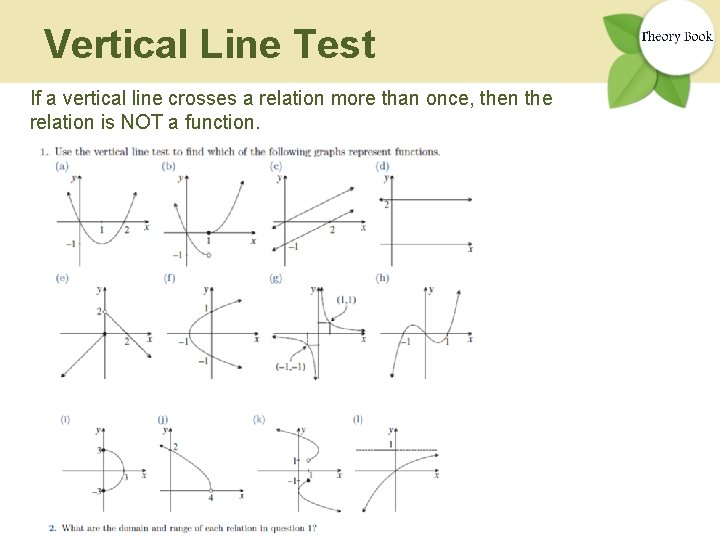
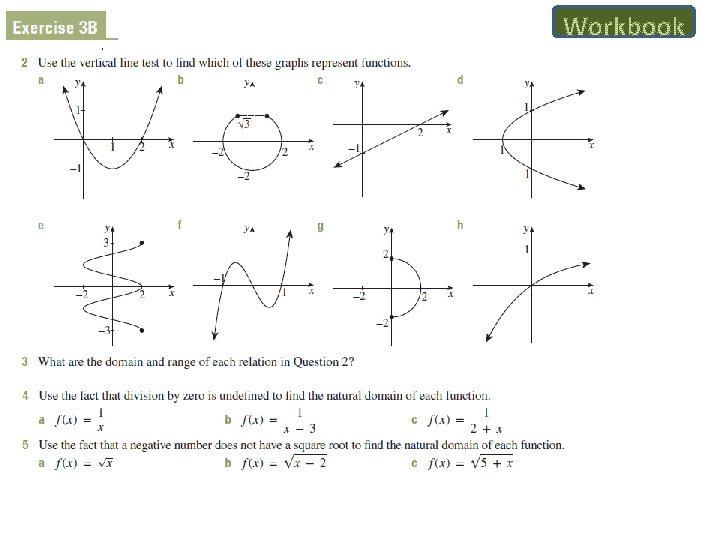
Vertical Line Test If a vertical line crosses a relation more than once, then the relation is NOT a function.

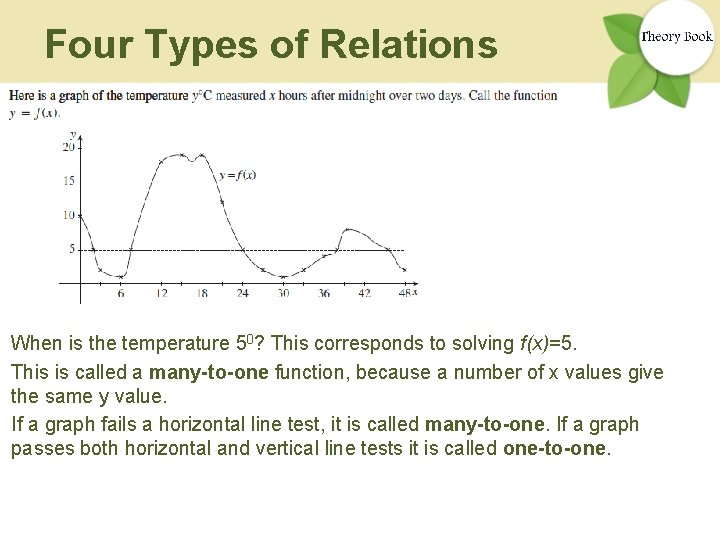
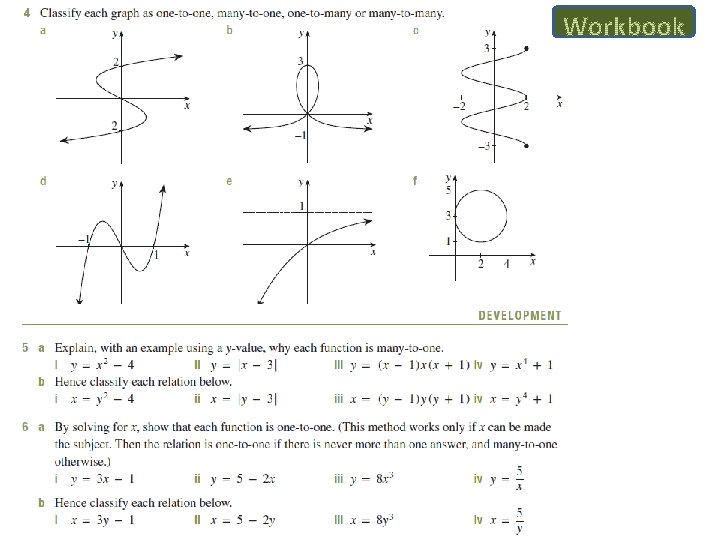
Four Types of Relations When is the temperature 50? This corresponds to solving f(x)=5. This is called a many-to-one function, because a number of x values give the same y value. If a graph fails a horizontal line test, it is called many-to-one. If a graph passes both horizontal and vertical line tests it is called one-to-one.

These are relations but not functions… Summary:

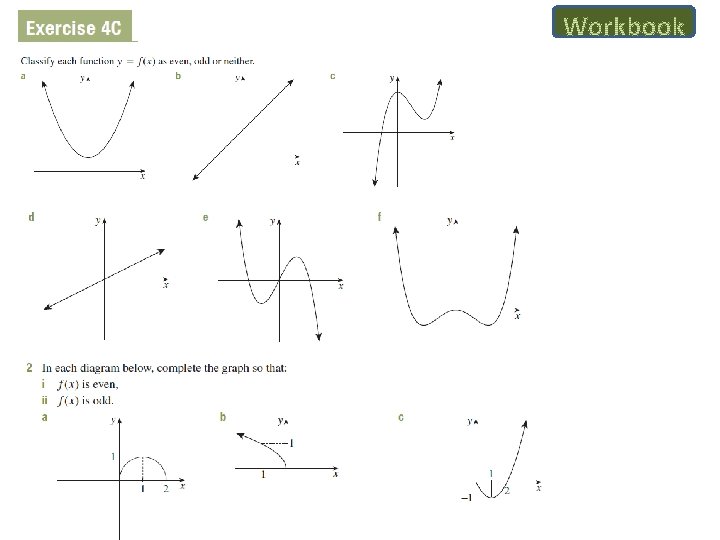
Odd and Even Functions An even function is one where f(-x) = f(x). It is symmetric about the y-axis. e. g. f(x) = x 2 is even, as f(-x) = (-x)2 = x 2 = f(x). An odd function is one where f(-x) = - f(x). It has point symmetry about the origin. e. g. f(x) = x 3 is odd, as f(-x) = -x 3 = -f(x). This means that the graph is mapped onto itself by a rotation of 1800 about the origin. NOTE: most functions are neither odd nor even. ###While we are looking at odd vs even functions here, we look at types of functions and actually graphing them in detail in F 1. 3###

Composite Functions Suppose that we are given the two functions: f (x) = x + 3 and g (x) = x 2. A composite function is when the result of one function is then substituted into the second function. e. g. g(f(x)) = (x+3)2 f(g(x)) = (x 2) +3 The notation is used for the composite function g(f(x)). If both f(x) and g(x) have the domain ‘for all real numbers’, then the composite function f(g(x)) or g(f(x)) has the same domain. Otherwise you need to consider the composite function carefully.