11 HAFTA VERLERN DZENLENMES VE NCEL VER ANALZ

11. HAFTA: VERİLERİN DÜZENLENMESİ VE NİCEL VERİ ANALİZİ II

İLİŞKİ ÖLÇÜMLERİ: SINIFLAMA DEĞİŞKENLERİ KORELASYON: İki değişlen arasındaki ilişkiyi veya bir değişkenin iki veya daha çok değişken ile olan ilişkisini test etmek, varsa bu ilişkinin derecesini ölçmek için kullanılır. Karşılıklı ilişkidir. REGRESYON: İki ya da daha fazla değişken arasındaki karşılıklı ilişkinin niteliğini gösterir. Örn: “Müşterinin tatmini müşterinin üründen memnun olması üzerinde etkilidir”. Burada müşteri tatmini ve müşteri memnuniyeti karşılıklı etkileşim içindedir. KOVARYANS: Korelasyonun standardize olmamış halidir.

KORELASYON ANALİZİ TÜRLERİ PARAMETRİK İLİŞKİ PARAMETRİK OLMAYAN BİRLİKTELİK KISMI KORELASYON ANALİZİ PEARSON SPEARMAN SIRA KORELASYON KATSAYISI KANDALL TAU b KATSAYISI Aralarında doğrusal bağlantı bulunan üç veya daha fazla değişken arasındaki ilişkinin düzeyi, büyüklüğü ve yönü diğer değşikenler sabit tutularak hesaplanır.

İlişki Analizi: Eşit aralıklı veya oranlı değişkenler Pearson’s r ilişki katsayısı ve Spearman sıra-ilişki katsayısı bir değişkeni bildiğiniz takdirde diğerini tahmin etmeye dayanır. r değeri gerçek değerle ortalama arasındaki farkların karelerinin toplamına eşittir. Eksi 1 ile artı 1 arasında değişir. 0 iki değişken arasında ilişki yok; 0 -0, 3 zayıf ilişki; 0, 3 -0, 6 orta ilişki; >0, 7 güçlü ilişki demektir Spearman sıra-ilişki katsayısı (rho) gerçek ölçüm değerleri yerine bu değerlerin sıralarını karşılaştırır

KORELASYON: HATIRLATMALAR Korelasyon ilişkisi bir neden sonuç ilişkisi olarak yorumlanmamalıdır. Elde edilen sonuç karşılıklı bir ilişkinin sonucudur. H 0=Başlangıç hipotezi-Boş Hipotez H 1= Alternatif hipotez-Araştırma Hipotezi Birlikte artarlarsa veya azalırlarsa pozitif korelasyon Biri artarken diğeri azalıyorsa ya da tersi negatif korelasyon 5

HİPOTEZ TESTLERİ Hipotez iki uçlu mu, tek uçlu mu? Yön var mı? Örn: Müşteri tatmini ve müşteri memnuniyeti pozitif ilişkilidir. Yani biri artıyorken diğeri de artıyorsa pozitif koralasyon vardır. (ONE TAILED) Yön yoksa ve sadece bir ilişkidir diyorsak TWO TAILED 2 Soru varsa “Zero Order Correlation” yapılır

HİPOTEZ TESTLERİ Öncelikle değişkenlere bakılır: Sürekli, kategorik, cinsiyet gibi versus süreksiz ve kategorik olmayan yaş gibi. Daha sonra dağılımlara bakılır: Örneğin: Kişi başı internet kullanma süresi. Gruplandırılmışsa süreksiz versus gruplandırılmamışsa sürekli dağılım gibi. 7

HİPOTEZ TESTLERİ CROHN BACH ALFA: 0, 95 üzeri sorunludur. Sorular birbirine çok benzer demektir. Ayırtedicilikleri yok demektir. Güvenilirlik aralığı: En az 0, 70 olmalıdır. İfade sayısı arttıkça sonuç da büyür. 0. 70 altında çıkmaz. Sorular az ise çok düşük çıkabilir. Güvenilirlik sorunu olduğundan değil. Zira ölçek formatif ölçek olabilir, çok güzel çalışıyor olabilir. BU anlamda alfanın düşük çıkması iyidir. Ölçeğin reflektif olup olmadığına bakmalıdır. 8

HİPOTEZ TESTLERİ KMO ANALİZİ: Minimum 0. 50 olmalıdır. Örneklem hacmi olarak evrenin %10’u anlamlıdır. Soru sayısının 2 ila 5 katı faktör analizi için givenilirlik sınırlarıdır. 9

Güvenilirlik Aralıkları Örneklem istatistikleri belirli bir güven düzeyinde evrene genellenebilir. Farklı örneklem istatistiklerinin her birinin farklı standart sapmaları yani standart hataları olabilir. Örneklem evren parameresine yaklaştıkça güvenirliği artar. %95 güven düzeyinde örneklem ortalaması evren parametresinden 1, 96, %99 güven düzeyinde 2, 575 standart hata uzaklıktadır.

Kİ KARE TESTİ: SERBESTLİK DERECESİ Kİ KARE TESTİ NEDİR? Ki kare değeri gözlenen değerle beklenen frekans değerler arasındaki farkın anlamlı olup olmadığına bakar. Yani ortak dağılımının tutarlılık düzeyini gösterir. Ki kare değerinin büyüklüğü böyle bir dağılımın gerçekleşme olasılığını test etme olanağı verir.

Ki Kare Hesabı: Serbestlik Derecesi Serbestlik derecesi bir istatistiksel modeldeki değişim olasılıkları demektir Örneğin ortalaması 11 olan 3 sayı bulun dersek sonsuz sayıda olasılık var (11, 11; 10, 11, 12; -11, 33; vs. ) Bu sayılardan biri 7 ise hala sonsuz olasılık var. Ama biri 7, diğeri 10 ise olasılık tek: 16 SD = N – 1

Ki Kare Hesabı: Serbestlik Derecesi Hangi durumlarda kullanılır? İki ya da daha fazla grup arasında fark olup olmadığına bakarken iki değişken arasında bağ (ilişki) olup olmadığını araştırırken Gruplararası homojenlik testinde Örneklemin hangi dağılıma uyup uymadığına bakarken

Ki kare 2 ( ) testi Diyelim ki, rastgele seçilen 100 deneğe (40 erkek, 60 kadın) geçen hafta kütüphaneye gidip gitmediklerini sorduk. Deneklerin %70’i gittiklerini söyledi. Kütüphaneye gitme açısından cinsiyete göre fark olup olmadığını nasıl test ederiz? “İki değişken (cinsiyet ve kütüphaneye gidip gitmeme) arasında evrende de ilişki yok” hipotezi (H 0) test ediliyor. Fark yoksa erkek ve kadınların yüzdelerinin birbirine eşit ya da yakın olması gerekli.

Küçük Örneklemlerde t Testi Z tablosu kullanılırken evrenin standart sapması biliniyormuş varsayımıyla hareket edilir. Çoğu durumda evrenin standart sapması bilinmiyor olsa bile örneklemin standart hatasından SS hesaplanır. T tablosu ise evrenin SS’i bilinmediği durumlarda SH hesaplamak için kullanılır ((X – μ) / (σ n)) Örneklem küçükse güven aralığı yükselir, büyükse düşer Denek sayısı 30’dan fazlaysa z, azsa t tablosu kullanılır.

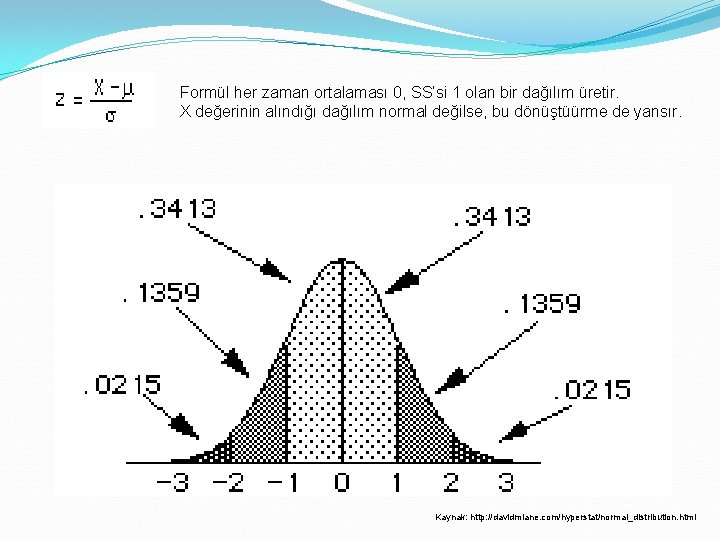
Z tablosu Artı eksi 3. 49 arasında değişir. Bu, teorik evrenin %99. 96’sına karşılık gelir. 1/10’luk aralarla standart sapmayı gösterir Örneğin, en üst satır -3. 4, -3. 41, -3. 42. . SS’yi gösteriyor z tablosundaki birkaç değerle ilgilidir. Birçok hipotez testinde %95 ve %99’luk alanlarla ilgilenir.

Formül her zaman ortalaması 0, SS’si 1 olan bir dağılım üretir. X değerinin alındığı dağılım normal değilse, bu dönüştüürme de yansır. Kaynak: http: //davidmlane. com/hyperstat/normal_distribution. html

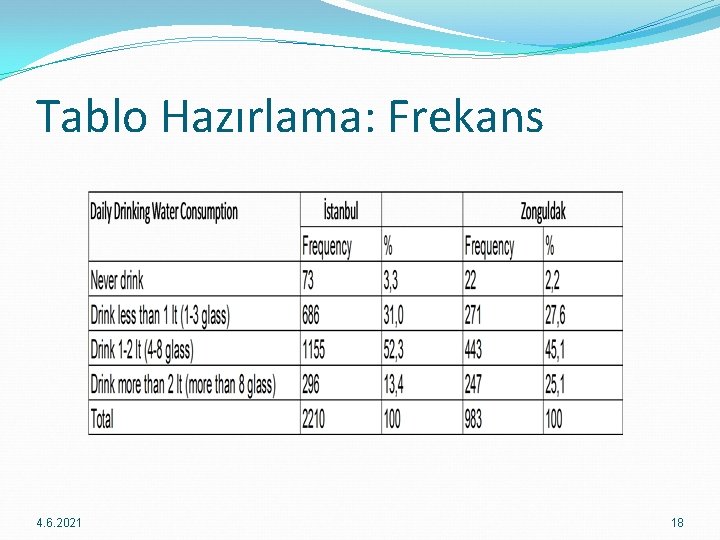
Tablo Hazırlama: Frekans 4. 6. 2021 18

GRAFİK HAZIRLAMA Çizgi Grafi. K Çubuk Grafik (Histogram) Pasta Grafik

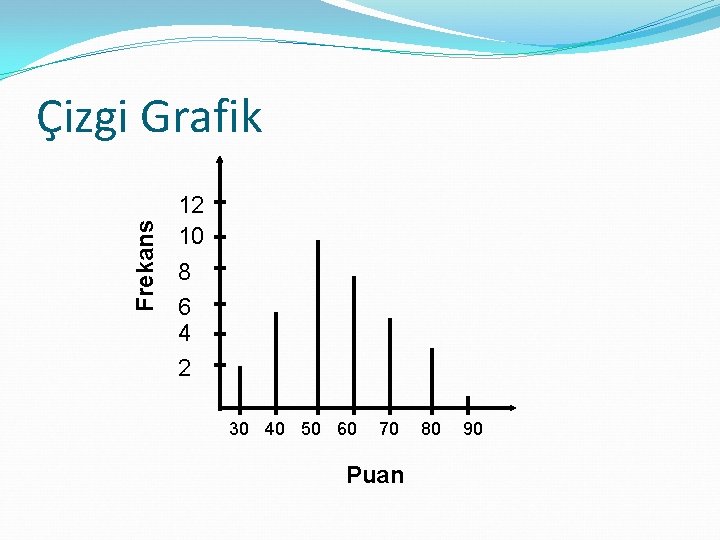
Frekans Çizgi Grafik 12 10 8 6 4 2 30 40 50 60 70 Puan 80 90

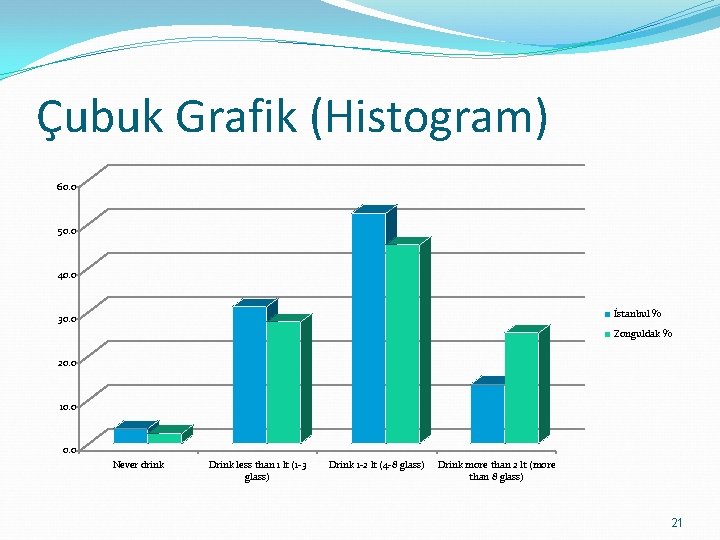
Çubuk Grafik (Histogram) 60. 0 50. 0 40. 0 İstanbul % 30. 0 Zonguldak % 20. 0 10. 0 Never drink Drink less than 1 lt (1 -3 glass) Drink 1 -2 lt (4 -8 glass) Drink more than 2 lt (more than 8 glass) 21

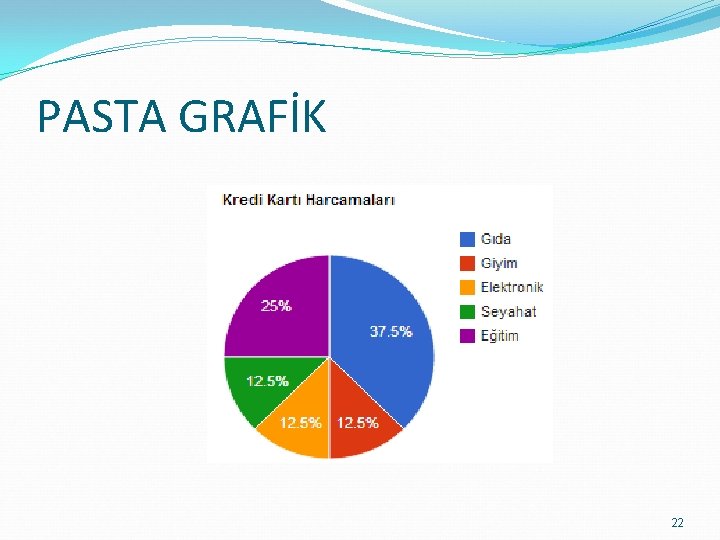
PASTA GRAFİK 22

Kaynaklar: Rauf Arıkan, Araştırma Yöntem ve Teknikleri, Nobel Yay. , Ankara, 2011 Ali Yıldırım, Hasan Şimşek, Sosyal Bilimlerde Nitel Araştırma Yöntemleri, Seçkin Yay. , Ankara, 2011 23