11 Electrical Field Theory Directed By Prof Dr

11 Electrical Field Theory Directed By: Prof. Dr. Ahmed Mohamed El-Sawy

Lecture Eleven • Energy Density in The Electrostatic Field • The Electric Dipole • Example 1 Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 2

Energy Density in The Electrostatic Field Derive the energy density in the electrostatic field in the form: When D & E are the electric flux density and the electric field intensity. Bringing a positive charge from infinity into the field of another positive charge requires work. Let Q 1, Q 2, Q 3 as follow: V 2, 1 the potential at Q 2 location due to Q 1. V 3, 1 R 13 = R 31 Q 1 Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory R 12 = R 21 V 2, 1 Q 2 R 23 = R 32 V 3, 2 Q 3 3

Energy Density in The Electrostatic Field Work to position Total positioning work = potential energy of field (1) (2) Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 4

Energy Density in The Electrostatic Field The summation between Eq(1) and Eq(2) yields the following: (3) V 1 = V 1, 2 + V 1, 3 + V 1, 4 + … V 2 = V 2, 2 + V 2, 3 + V 2, 4 + … (4) V 3 = V 3, 2 + V 3, 3 + V 3, 4 + … Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 5

Energy Density in The Electrostatic Field By substituting Eq(3) into Eq(4) yields the following: 2 WE = Q 1 V 1 + Q 2 V 2 + Q 3 V 3 + … WE = Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 6

Energy Density in The Electrostatic Field Using Maxwell’s first equation, replace ρν by its equal ∇·D ∇·(V D) ≡ V (∇·D) + D·(∇V ) Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 7

Energy Density in The Electrostatic Field Using the divergence Theorem, we have: Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 8

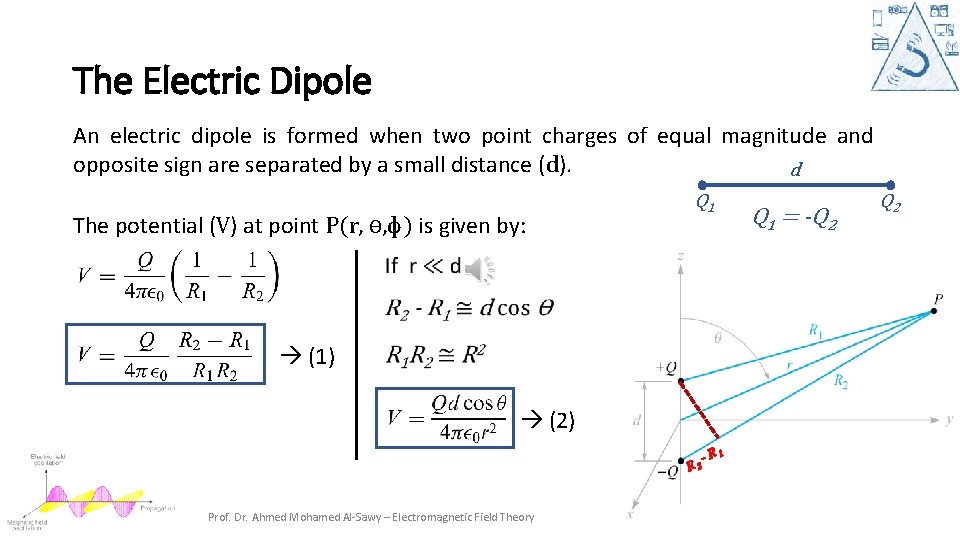
The Electric Dipole An electric dipole is formed when two point charges of equal magnitude and opposite sign are separated by a small distance (d). d The potential (V) at point P(r, Ө, ф) is given by: Q 1 = -Q 2 (1) (2) R 2 Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory - R 1 9

The Electric Dipole From Eq(1) and Eq(2), we have: The dipole moment = P = Q d If the dipole center is not at the origin but at r´ so, Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 10

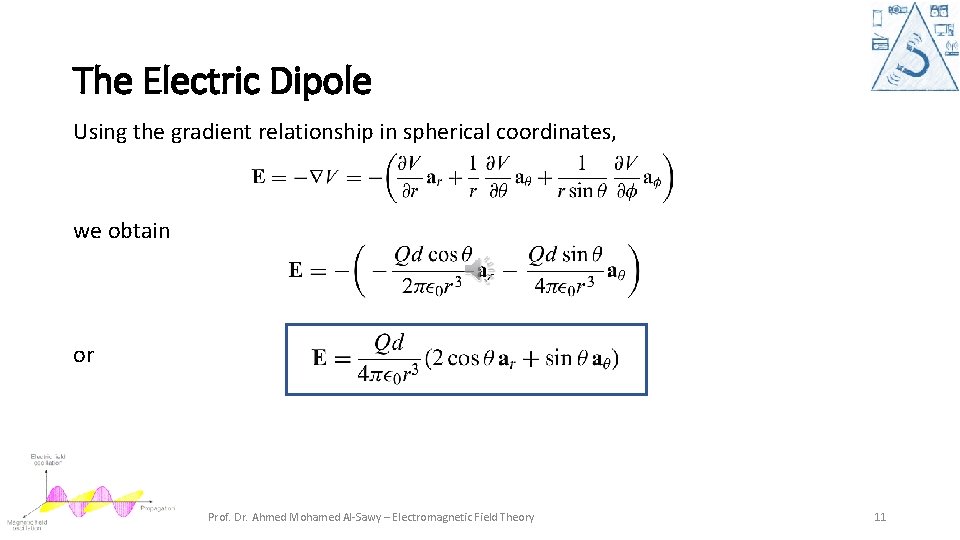
The Electric Dipole Using the gradient relationship in spherical coordinates, we obtain or Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 11

The Electric Dipole Example 1 Two dipoles with dipole moments -5 az n. C/m and 9 az n. C/m are located at points (0, 0, -2 ) and (0, 0, 3), respectively. Find the potential at the origin. Solution. where Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 12

The Electric Dipole Example 1 Hence, Prof. Dr. Ahmed Mohamed Al-Sawy – Electromagnetic Field Theory 13