11 4 The Cross product For an animation

11. 4 The Cross product For an animation of this topic visit: http: //www. math. umn. edu/~nykamp/m 2374/readings/crossprod Red x Green = Blue /

What is the cross product? • a × b is a vector that is perpendicular to both a and b. • ||a × b|| is the area of the parallelogram spanned by a and b (i. e. the parallelogram whose adjacent sides are the vectors a and b). • The direction of a×b is determined by the righthand rule. (This means that if we curl the fingers of the right hand from a to b, then the thumb points in the direction of a × b. )

Definition of Cross Product of Two Vectors in Space Find the cross product of vectors (by hand with a calculator) u = 3 i +2 j – k v = i + 2 k Note: To find a cross product on the TI 89 Press 2 nd 5 (math) – 4 matrix – L Vector ops - cross. P([3, 2, -1], [1, 0, 2])

Definition of Cross Product of Two Vectors in Space For an explanation and animation of the cross product visit: http: //www. math. umn. edu/~nykamp/m 2374/readings/ crossprod/

Example 1 • • • Find the cross product of the two vectors u = i – 2 j + k v = 3 i + j – 2 k Find u x v Find v x u Find v x v

Example 1 • • • Find the cross product of the two vectors u = i – 2 j + k v = 3 i + j – 2 k Find u x v Find v x u Find v x v

Example 1 continued • u = i – 2 j + k v = 3 i + j – 2 k • Find a unit vector that is orthogonal to u and v

The Triple Scalar Product

Geometric Property of Triple Scalar

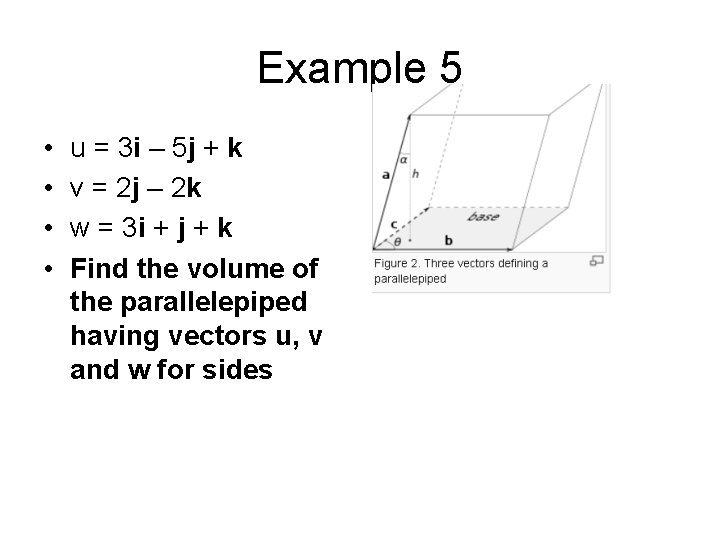
Example 5 • • u = 3 i – 5 j + k v = 2 j – 2 k w = 3 i + j + k Find the volume of the parallelepiped having vectors u, v and w for sides

Example 5 hint This works because bxc yields a vector perpendicular to a and b in with the magnitude of the area of the parallelogram formed (the base of the parallel piped) bxc points in the direction of the height of the parallelepiped when dotted with a this gives the magnitude of bxc times the portion of a that points in the direction of bxc (the direction of the height )in other words this gives us the same as the formula Bh

Q: Why should you never make a math teacher angry? A: You might get a cross product Q: What do you get when you cross an elephant and a banana? A: | elephant | * | banana | * sin(theta)

Proof of the cross product proof that the cross product is orthogonal to the two original vectors is part of the homework │u x v │ = │u │ │v │sinθ