11 3 THE SHORTRUN BEHAVIOR OF POLYNOMIALS 1

11. 3 THE SHORT-RUN BEHAVIOR OF POLYNOMIALS 1

Visualizing Short-Run and Long-Run Behaviors of a Polynomial Example 1 Compare the graphs of the polynomials f, g, and h given by f(x) = x 4 − 4 x 3 + 16 x − 16, g(x) = x 4 − 4 x 3 − 4 x 2 + 16 x, h(x) = x 4 + x 3 − 8 x 2 − 12 x. A close-up look near zeros and turns A larger scale look resembling x 4 2

Factored Form, Zeros, and the Short. Run Behavior of a Polynomial Example 2 Investigate the short-run behavior of the third degree polynomial u(x) = x 3 − x 2 − 6 x. (a) Rewrite u(x) as a product of linear factors. (b) Find the zeros of u(x). Solution (a) u(x) = x (x 2 – x – 6) = x (x + 2) (x – 3) (b) u(x) = 0 if and only if one of its linear factors is zero, so the zeros of u(x) occur at x = 0, x = -2, and x = 3. 3

Example 2 (continued) Investigate the short-run behavior of the third degree polynomial u(x) = x 3 − x 2 − 6 x = x (x + 2) (x – 3). (c) Describe the graph of u(x). Where does it cross the xaxis? the y-axis? Where is u(x) positive? Negative? y = x 3 y =u(x) ← u positive ↘ (0, 0) (3, 0) (-2, 0) u negative → ↖ u negative The graph of u(x) has zeros at x = -2, 0, and 3. The function changes sign at each of these zeros. Its long-run behavior resembles y = x 3. 4

Factors and Zeros of Polynomials Suppose p is a polynomial. • If the formula for p has a linear factor, that is, a factor of the form (x − k), then p has a zero at x = k. • Conversely, if p has a zero at x = k, then p has a linear factor of the form (x − k). 5

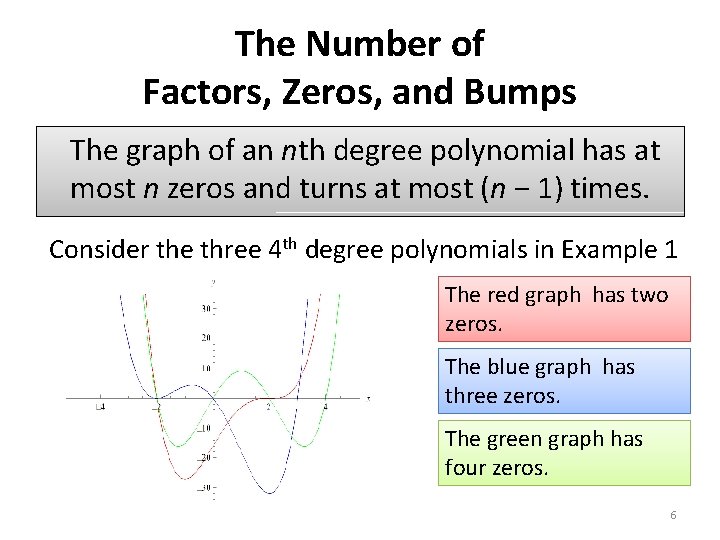
The Number of Factors, Zeros, and Bumps The graph of an nth degree polynomial has at most n zeros and turns at most (n − 1) times. Consider the three 4 th degree polynomials in Example 1 The red graph has two zeros. The blue graph has three zeros. The green graph has four zeros. 6

Multiple Zeros If p is a polynomial with a repeated linear factor, then p has a multiple zero. • If the factor (x − k) occurs an even number of times, the graph of y = p(x) does not cross the x-axis at x = k, but “bounces” off the xaxis at x = k. • If the factor (x − k) occurs an odd number of times, the graph of y = p(x) crosses the xaxis at x = k, but it looks flattened there. 7

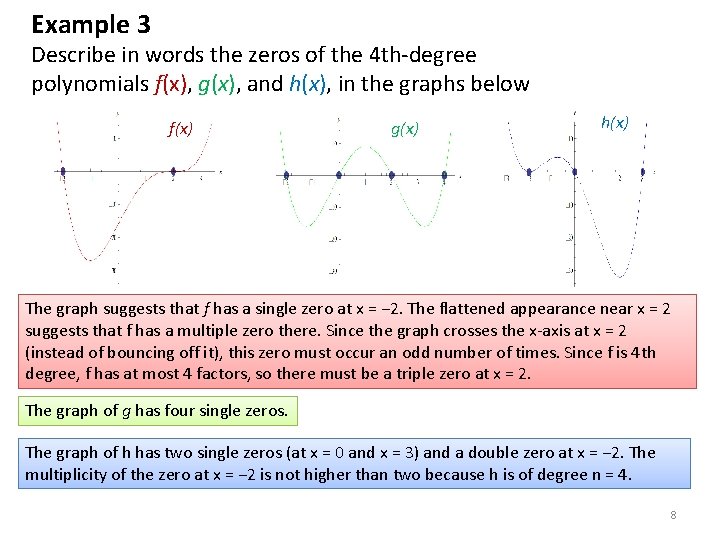
Example 3 Describe in words the zeros of the 4 th-degree polynomials f(x), g(x), and h(x), in the graphs below f(x) g(x) h(x) The graph suggests that f has a single zero at x = − 2. The flattened appearance near x = 2 suggests that f has a multiple zero there. Since the graph crosses the x-axis at x = 2 (instead of bouncing off it), this zero must occur an odd number of times. Since f is 4 th degree, f has at most 4 factors, so there must be a triple zero at x = 2. The graph of g has four single zeros. The graph of h has two single zeros (at x = 0 and x = 3) and a double zero at x = − 2. The multiplicity of the zero at x = − 2 is not higher than two because h is of degree n = 4. 8

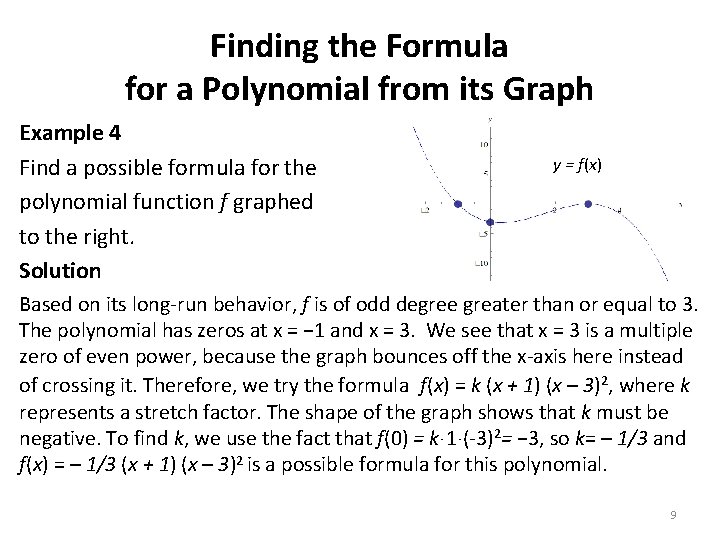
Finding the Formula for a Polynomial from its Graph Example 4 Find a possible formula for the polynomial function f graphed to the right. Solution y = f(x) Based on its long-run behavior, f is of odd degree greater than or equal to 3. The polynomial has zeros at x = − 1 and x = 3. We see that x = 3 is a multiple zero of even power, because the graph bounces off the x-axis here instead of crossing it. Therefore, we try the formula f(x) = k (x + 1) (x – 3)2, where k represents a stretch factor. The shape of the graph shows that k must be negative. To find k, we use the fact that f(0) = kˑ 1ˑ(-3)2= − 3, so k= – 1/3 and f(x) = – 1/3 (x + 1) (x – 3)2 is a possible formula for this polynomial. 9