11 10 Taylor and Maclaurin Series The purpose

Taylor and Maclaurin Series Taylor series ize or m e M iz u Q

Taylor and Maclaurin Series or f e iz u Q iz r o m

Taylor and Maclaurin Series Taylor’s Inequality iz Memo Qu r o f e riz

Taylor and Maclaurin Series We start by supposing that f is any function that

Taylor and Maclaurin Series We can differentiate the series in Equation 1 term by

Taylor and Maclaurin Series Let’s apply the procedure one more time. Differentiation of the

Taylor and Maclaurin Series Solving this equation f (n)(a) = n!cn for the nth

Taylor and Maclaurin Series Substituting this formula for cn back into the series, we

Maclaurin Series For the special case a = 0 the Taylor series becomes !

Video Examples: Intro: Mac. Lauren Series: https: //www. youtube. com/watch? v=epgwuzz. DHs. Q Taylor

This means a=1 in your Taylor Series This tells you to go up to

2 a. Find the Maclaurin polynomial of degree 6 for f(x)=cos(x) 6 0 18

Taylor Polynomial when not given degree: In the last example if we were told

Also write the sum of the series in summation form Note: not given the

Textbook Example 1 Find the Maclaurin series of the function f (x) = ex

Example 1 – Solution cont’d To find the radius of convergence we let an

Taylor and Maclaurin Series Important Maclaurin Series and Their Radii of Convergence ! e

Additional Information: (For 11. 11) In trying to show that limn Rn(x) = 0

Homework: Page 811 # 6 -18 even, (skip # 12), 19 29

Slides: 29

Download presentation

Taylor and Maclaurin Series Taylor series ize or m e M iz u Q r o f Maclaurin series 2

Taylor and Maclaurin Series or f e iz u Q iz r o m Me Important Maclaurin Series and Their Radii of Convergence 3

Taylor and Maclaurin Series Taylor’s Inequality iz Memo Qu r o f e riz 4

Taylor and Maclaurin Series We start by supposing that f is any function that can be represented by a power series (Lesson 10. 9) f (x) = c 0 + c 1(x – a) + c 2(x – a)2 + c 3(x – a)3 + c 4(x – a)4 +. . . | x – a | < R Let’s try to determine what the coefficients cn must be in terms of f. (In other words, find all the coefficients) To begin, notice that if we put x = a in Equation 1, then all terms after the first one are 0 and we get f (a) = c 0 5

Taylor and Maclaurin Series We can differentiate the series in Equation 1 term by term: f (x) = c 1 + 2 c 2(x – a) + 3 c 3(x – a)2 + 4 c 4(x – a)3 +. . . | x – a | < R and substitution of x = a in Equation 2 gives f (a) = c 1 Now we differentiate both sides of Equation 2 and obtain f (x) = 2 c 2 + 2 3 c 3(x – a) + 3 4 c 4(x – a)2 +. . . | x – a | < R Again we put x = a in Equation 3. The result is f (a) = 2 c 2 6

Taylor and Maclaurin Series Let’s apply the procedure one more time. Differentiation of the series in Equation 3 gives f '''(x) = 2 3 c 3 + 2 3 4 c 4(x – a) + 3 4 5 c 5(x – a)2 +. . . | x – a| < R and substitution of x = a in Equation 4 gives f '''(a) = 2 3 c 3 = 3!c 3 By now you can see the pattern. If we continue to differentiate and substitute x = a, we obtain f (n)(a) = 2 3 4 . f (n)(a) = n!cn . . ncn = n!cn 7

Taylor and Maclaurin Series Solving this equation f (n)(a) = n!cn for the nth coefficient cn, we get This formula is valid even for n = 0. Note that 0! = 1 and f (0) = f. Thus we have proved the following theorem. 8

Taylor and Maclaurin Series Substituting this formula for cn back into the series, we see that if f has a power series expansion at a, then it must be of the following form. coefficients y! p Co The series in Equation 6 is called the Taylor series of the function f at a (or about a or centered at a). 9

Maclaurin Series For the special case a = 0 the Taylor series becomes ! py o C This case arises frequently enough that it is given the special name Maclaurin series. Note: 10

Taylor Series vs. Maclaurin 11

a a 12

Video Examples: Intro: Mac. Lauren Series: https: //www. youtube. com/watch? v=epgwuzz. DHs. Q Taylor Series: https: //www. youtube. com/watch? v=1 Lxh. Xq. D 3_CE&ebc=ANy. Px. Kp. B e. QVYJMjh. Bcs. Wc 3 bl 3 xiwf. Yp. Uw. Pm. WLU-ZJr 0 sn 4 tss. Pu. SHg. Wmq. FAj. OUAVq. Ohk. V 713 VNKPf. Gva. FWp. Oqp. EGhs. W 1 e. H 4 YA Examples: Calculus Expert: https: //www. youtube. com/watch? v=C 1 vc. VMotnkg Patrick. JMT: https: //www. youtube. com/watch? v=cj. Po. EZ 0 I 5 w. Q Kahn Academy: https: //www. youtube. com/watch? v=WWe 7 p. Zjc 4 s 8&ebc=ANy. Px. Kp. Be. QVYJMjh. Bcs. Wc 3 bl 3 xiwf. Yp. Uw. Pm. WLU-ZJr 0 sn 4 tss. Pu. SHg. Wmq. FA 13 j. OUAVq. Ohk. V 713 VNKPf. Gva. FWp. Oqp. EGhs. W 1 e. H 4 YA

y! p o C 0 1 2 3 14

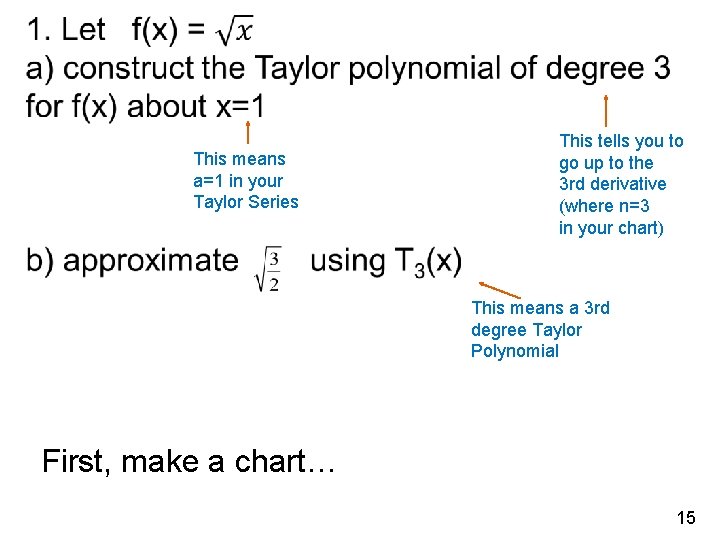
This means a=1 in your Taylor Series This tells you to go up to the 3 rd derivative (where n=3 in your chart) This means a 3 rd degree Taylor Polynomial First, make a chart… 15

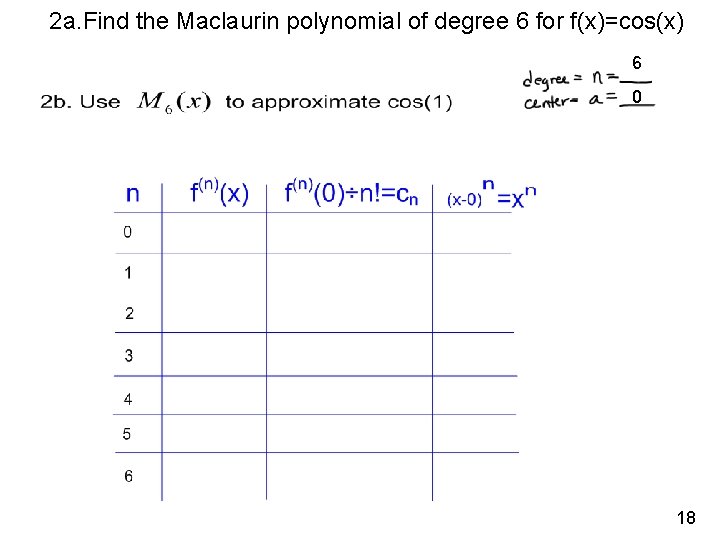
2 a. Find the Maclaurin polynomial of degree 6 for f(x)=cos(x) 6 0 18

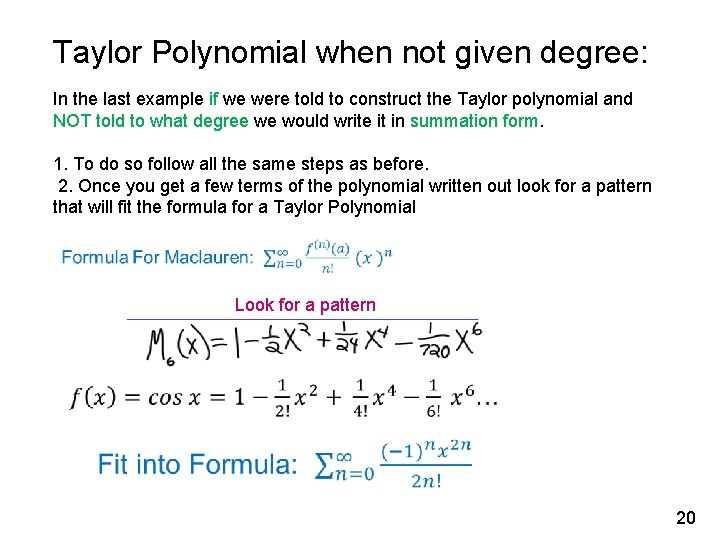
Taylor Polynomial when not given degree: In the last example if we were told to construct the Taylor polynomial and NOT told to what degree we would write it in summation form. 1. To do so follow all the same steps as before. 2. Once you get a few terms of the polynomial written out look for a pattern that will fit the formula for a Taylor Polynomial Look for a pattern 20

Also write the sum of the series in summation form Note: not given the degree. 21

Textbook Example 1 Find the Maclaurin series of the function f (x) = ex and its radius of convergence. 23

Textbook Example 1 ex ex 1 24

Textbook Example 1 25

Example 1 – Solution cont’d To find the radius of convergence we let an = xn/n!. Then so, by the Ratio Test, the series converges for all x and the radius of convergence is R =. 26

Taylor and Maclaurin Series Important Maclaurin Series and Their Radii of Convergence ! e iz r o m Me Table 1 27

Additional Information: (For 11. 11) In trying to show that limn Rn(x) = 0 for a specific function f, we usually use the following Theorem. 28

Homework: Page 811 # 6 -18 even, (skip # 12), 19 29