104 Choosing the pivot column and pivot row

10/4 Choosing the pivot column and pivot row in the simplex algorithm 1 Find the most negative entry in the bottom row. This determines the pivot column. Bringing this variable into solution increases the objective the quickest. Note: If there are no negative entries you are already at the maximum value. Stop. 2 Calculate all the positive ratios in the pivot column. Find the smallest one. This determines the pivot row.

Question: How do you spot an unbounded problem with no solution when you are using the simplex algorithm? Two examples: 1. Maximize P = 2 x + y, where x, y>= 0, y >= x, and y<=x+2

2. Maximize P = -2 x + y, where x, y>= 0, y >= x, and y<=x+2 This example shows that P can have a maximum on an unbounded region

10/4 The simplex algorithm 1 Find the most negative entry in the bottom row. This determines the pivot column. Bringing this variable into solution increases the objective the quickest. Note: If there are no negative entries you are already at the maximum value. Stop. 2 Calculate all the positive ratios in the pivot column. Find the smallest one. This determines the pivot row. Note: if there are no positive ratios in the column, the problem is unbounded and has no maximum. Stop. 3 Perform a pivot operation using the entry in the pivot row and pivot column. 4 Repeat steps 1 thru 3 until you reach the maximum or discover the problem is unbounded

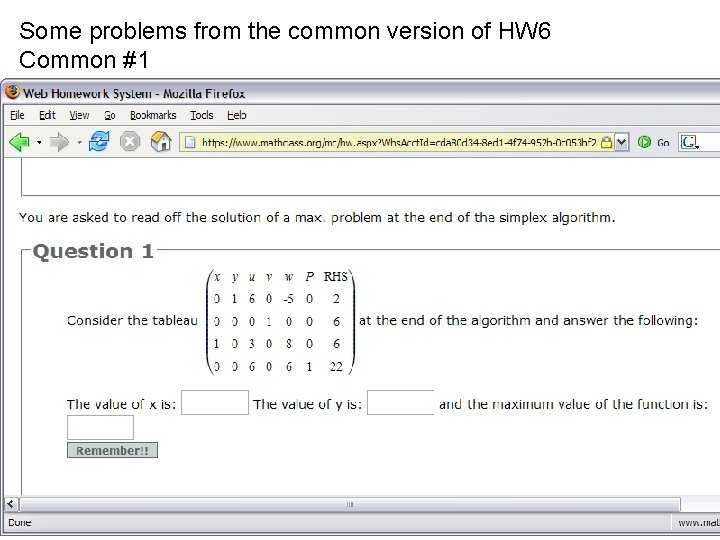
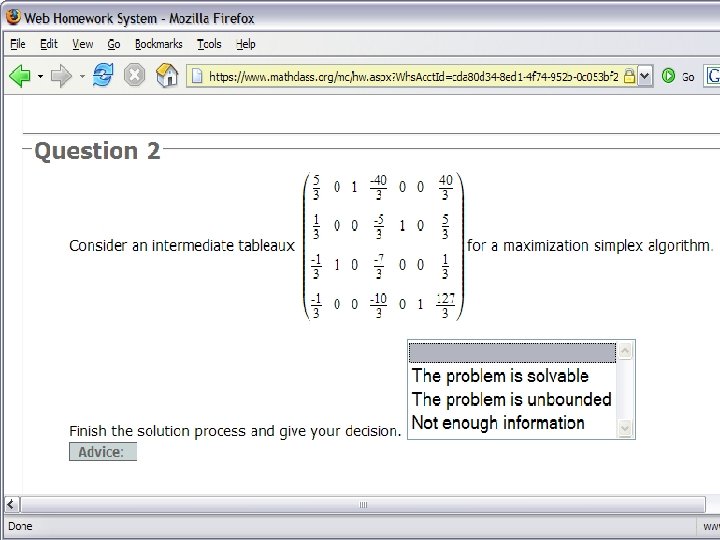
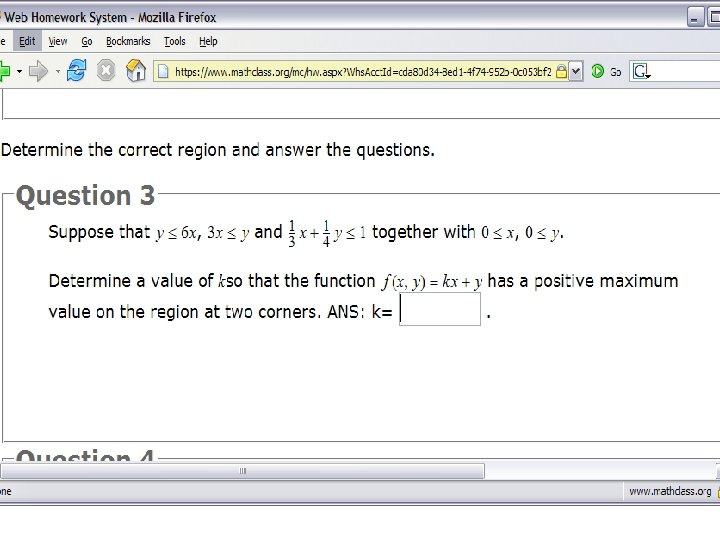
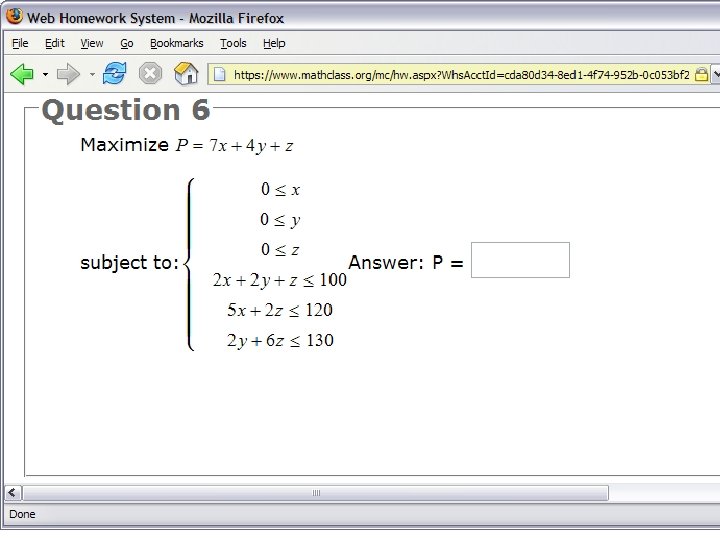
Some problems from the common version of HW 6 Common #1

Setting up linear programming problems: A farmer has 150 acres of land suitable for crops A and B. The cost of growing A is $40/acre. The cost for B is $60/acre The farmer has $7600 captial available. Each acre of A takes 20 hrs of labor and each acre of B takes 25 hrs of labor. The farmer has 3300 hrs of labor available. He expects to Make $150/acre for A and $200/acre for B. How many acres of each crop should he plant to maximize his profit?