100 100 200 200 300 300 400 400













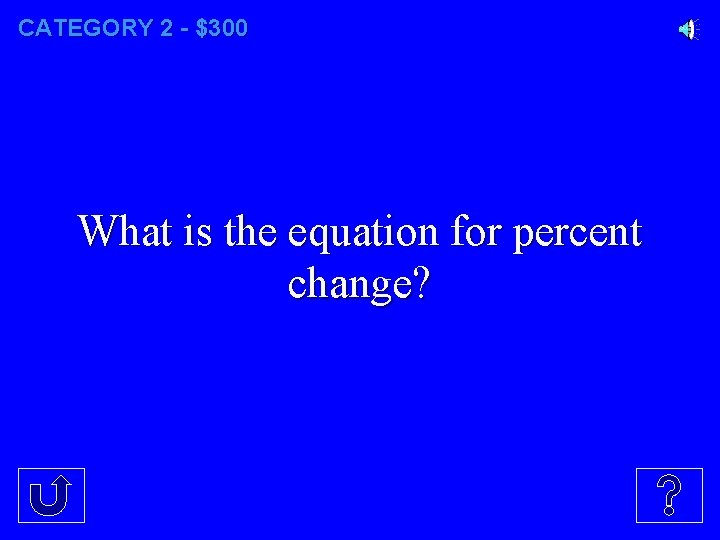









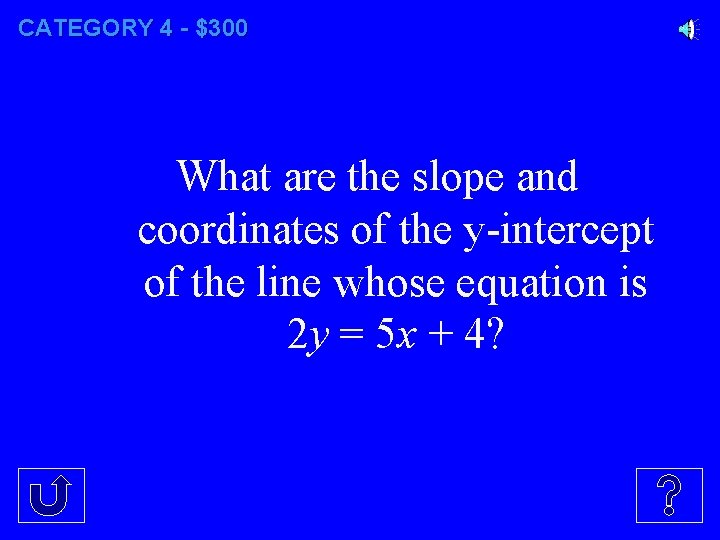


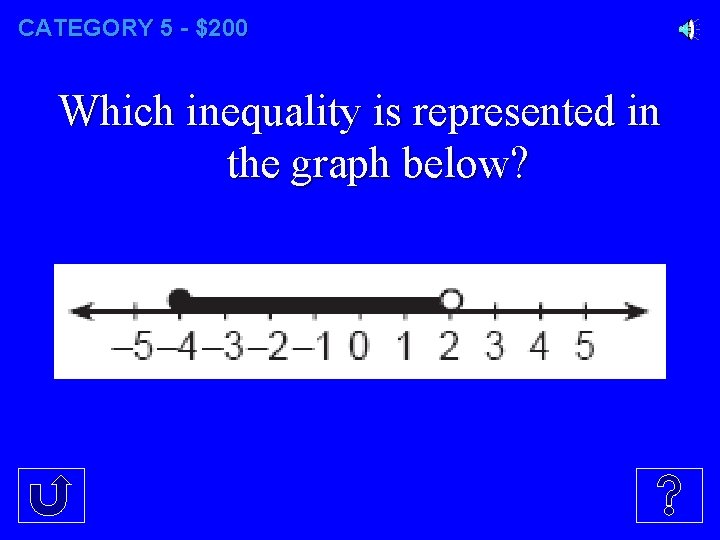

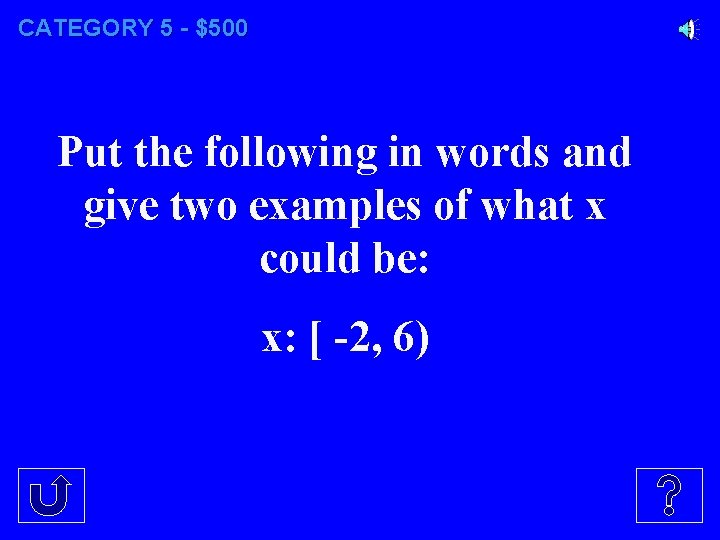










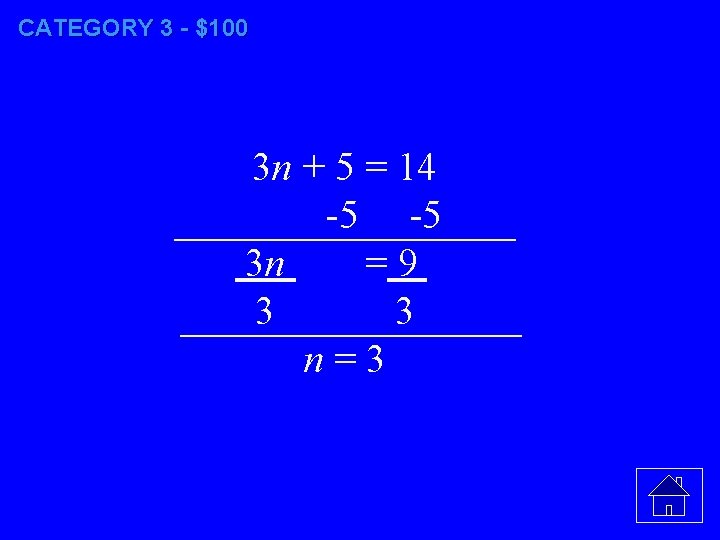
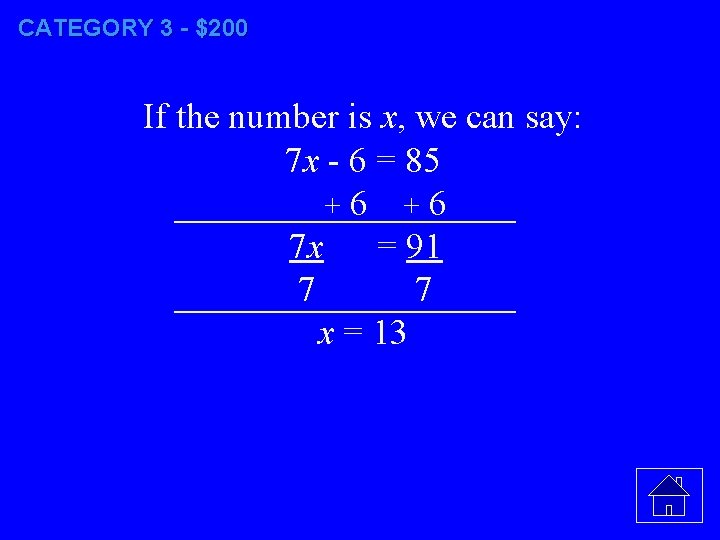







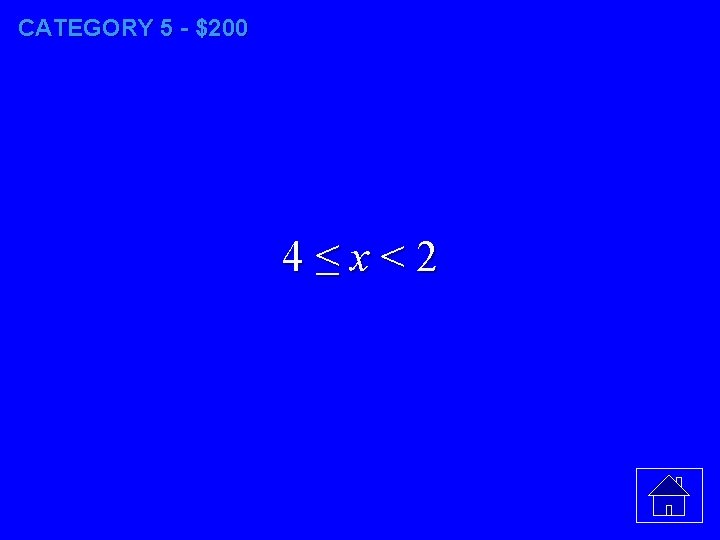


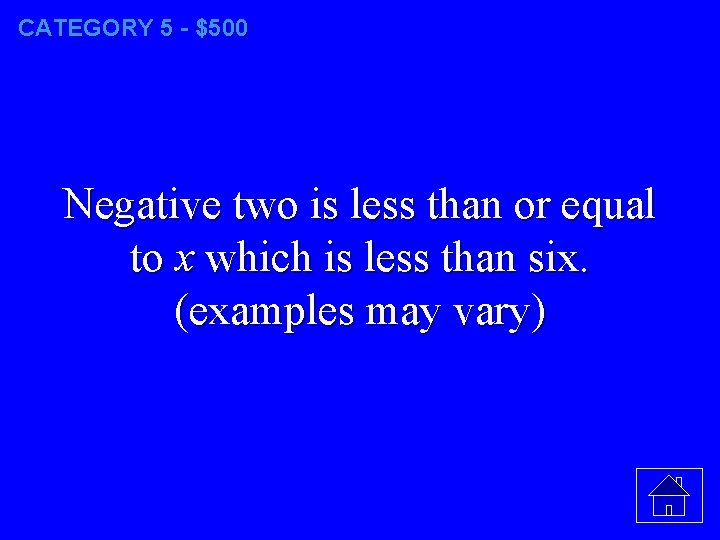
- Slides: 57


$100 $100 $200 $200 $300 $300 $400 $400 $500 $500

Properties of Real Numbers

Ratios and Percents

Solving Linear Equations

Graphing Linear Equations

Inequalities

Properties of Real Numbers Ratios and Percents Solving Linear Equations Graphing Linear Equations Inequalities $100 $100 $200 $200 $300 $300 $400 $400 $500 $500

CATEGORY 1 - $100 Give an example of the Commutative Property of Addition?

CATEGORY 1 - $200 Define the following: Integer

CATEGORY 1 - $300 What is the quotient of 0 and 5? What is the quotient of 5 and 0?

CATEGORY 1 - $400 Put the following numbers in order from least to greatest: 5 ¾ , -2, ∞, -2. 2, /5, 0. 6

CATEGORY 1 - $500 List one property that holds true for multiplication, but does NOT hold true for division.

CATEGORY 2 - $100 Is it possible to have 300%? Explain your reasoning.

CATEGORY 2 - $200 How do you convert from a decimal to a percent?
CATEGORY 2 - $300 What is the equation for percent change?

CATEGORY 2 - $400 Find the percent of change and describe it as an increase or decrease: 26 to 20

CATEGORY 2 - $500 An item costs $64. The price is increased by $10, then reduced by $10. Is the percent of increase equal to the percent of decrease? Explain your answer.

CATEGORY 3 - $100 In the equation 3 n + 5 = 14, n is equal to. . .

CATEGORY 3 - $200 At the beginning of her mathematics class, Ms. Smith gives a warm-up problem. She says, “I am thinking of a number such that 6 less than the product of 7 and this number is 85. ” Which number is she thinking of?

CATEGORY 3 - $300 If a + 3 b = 13 and a = 7 the value of b is. . .

CATEGORY 3 - $400 What is the point of intersection of the graphs of the lines 2 x – y = 3 and x + y = 3?

CATEGORY 3 - $500 Mario paid $44. 25 in taxi fare from the hotel to the airport. The cab charged $2. 25 for the first mile plus $3. 50 for each additional mile. How many miles was it from the hotel to the airport?

CATEGORY 4 - $100 Given two points, how do you calculate the slope of a line?

CATEGORY 4 - $200 How do you know if two lines will intersect?
CATEGORY 4 - $300 What are the slope and coordinates of the y-intercept of the line whose equation is 2 y = 5 x + 4?

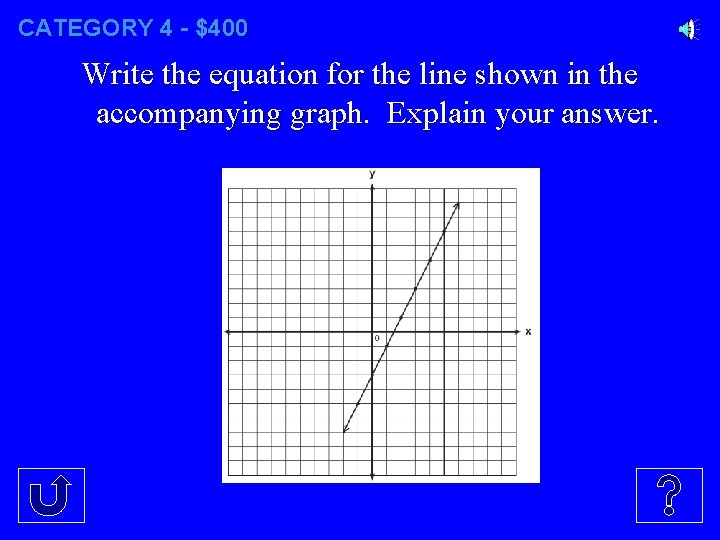
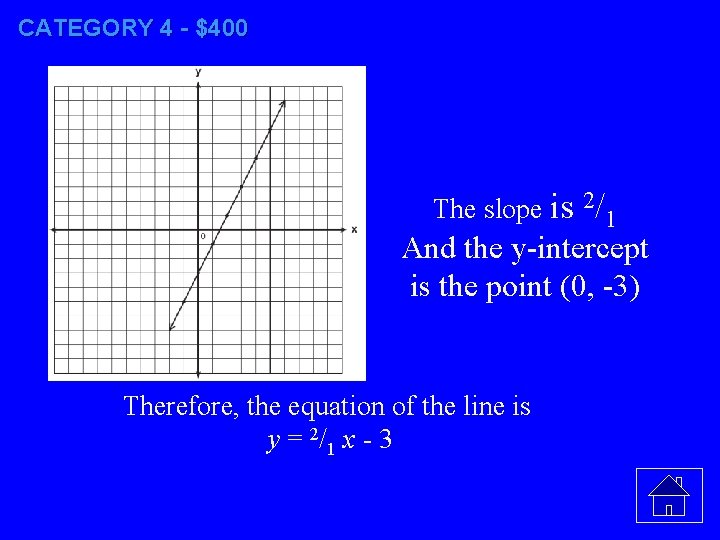
CATEGORY 4 - $400 Write the equation for the line shown in the accompanying graph. Explain your answer.

CATEGORY 4 - $500 Write the equation of a line Perpendicular to line below and that goes through the point (0, 5). 3 x + 2 y = 4

CATEGORY 5 - $100 Is the ordered pair (2, 5) in the solution set of: y > 2 x + 1?
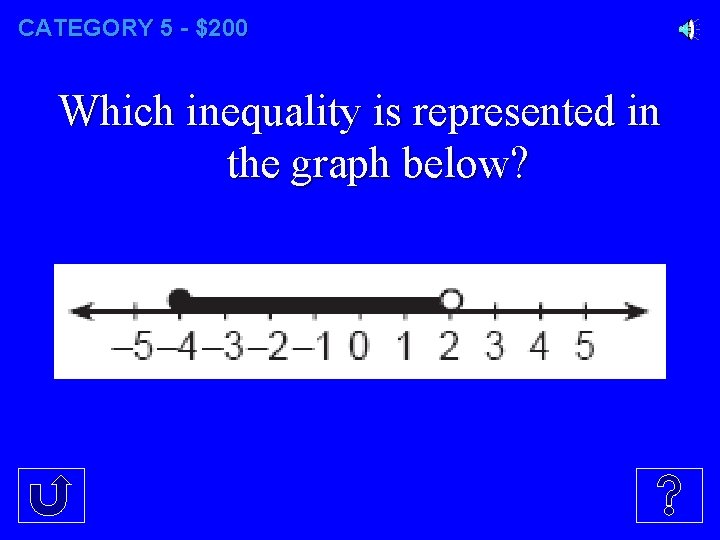
CATEGORY 5 - $200 Which inequality is represented in the graph below?

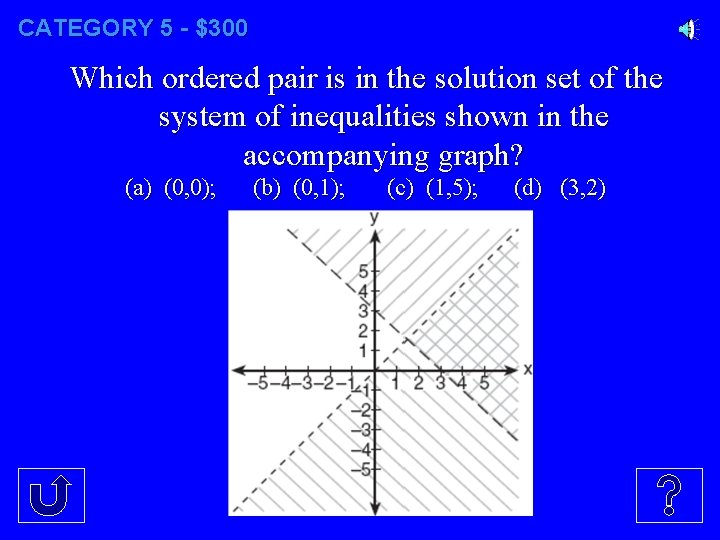
CATEGORY 5 - $300 Which ordered pair is in the solution set of the system of inequalities shown in the accompanying graph? (a) (0, 0); (b) (0, 1); (c) (1, 5); (d) (3, 2)

CATEGORY 5 - $400 Thelma and Laura start a lawn-mowing business and buy a lawnmower for $225. They plan to charge $15 to mow one lawn. What is the minimum number of lawns they need to mow if they wish to earn a profit of at least $750?
CATEGORY 5 - $500 Put the following in words and give two examples of what x could be: x: [ -2, 6)

CATEGORY 1 - $100 Answers may vary Example: 5 + 3 = 3 + 5

CATEGORY 1 - $200 A whole number.

CATEGORY 1 - $300 0/5=0 5 / 0 = UNDEFINED

CATEGORY 1 - $400 - ∞, -2. 2, -2, 0. 6, ¾ , 5/5, ∞

CATEGORY 1 - $500 The Commutative Property

CATEGORY 2 - $100 Yes! Your money can triple, or in other words, grow 300%.

CATEGORY 2 - $200 Multiply by 100, or in other words, move the decimal point two places to the right.

CATEGORY 2 - $300 Percent Change = ( New – Original ) x 100

CATEGORY 2 - $400 The Percent Change is a Decrease by 23%

CATEGORY 2 - $500 The percent of increase is NOT equal to the percent of decrease. When the cost is increased by $10 (from $64 to $74), this is a 15. 6% increase. When the cost is decreased by $10 (from $74 to $64) this is a 13. 5% decrease.
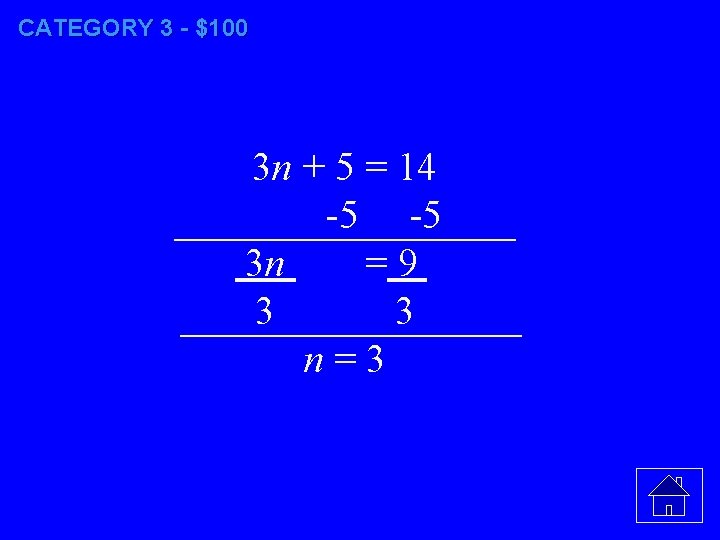
CATEGORY 3 - $100 3 n + 5 = 14 -5 -5 3 n =9. 3 3 n=3
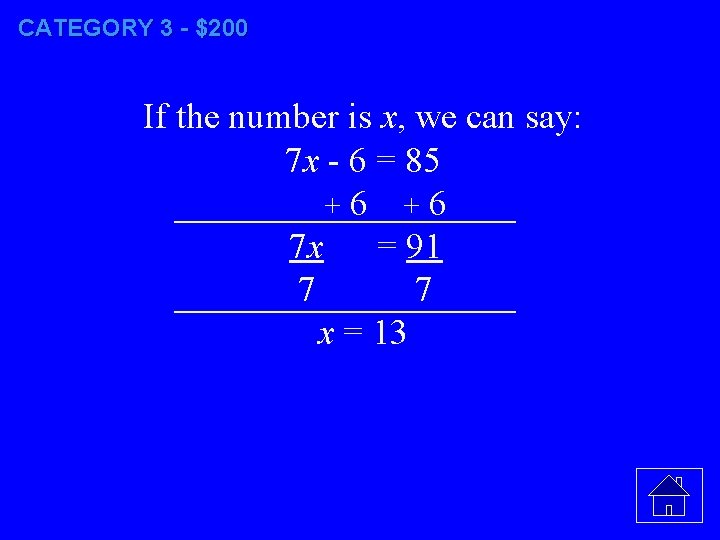
CATEGORY 3 - $200 If the number is x, we can say: 7 x - 6 = 85 +6 +6 7 x = 91 7 7 x = 13

CATEGORY 3 - $300 a + 3 b = 13 7 + 3 b = 13 -7 -7 3 b = 6 3 3 b=2

CATEGORY 3 - $400 If 2 x – y = 3, then we can say y = 2 x - 3 If x + y = 3, then we can say y = -x + 3 We have: y = -x + 3 = 2 x – 3 = y Or -x + 3 = 2 x – 3 6 = 3 x 2=x When x = 2, y = -2 + 3 = 1 Therefore, the point of intersection is (2 , 1)

CATEGORY 4 - $100 y 2 – y 1 Slope = x 2 – x 1

CATEGORY 4 - $200 If two lines have different slopes, they will intersect.

CATEGORY 4 - $300 If 2 y = 5 x + 4, then we can say y = 5/2 x + 2 Therefore, the slope (m) is 5/2 And the y-intercept (b) is the point (0, 2)

CATEGORY 4 - $400 The slope is 2/1 And the y-intercept is the point (0, -3) Therefore, the equation of the line is y = 2/1 x - 3

CATEGORY 4 - $500 We can rewrite the equation of the line in slope intercept form as follows: 3 x + 2 y = 4 -3 x 2 y = -3 x + 4 2 2 So, y = -3/2 x + 2 Therefore, the slope of the perpendicular line must be 2/3 You should realize that the y-intercept is 5. 2/ x + 5 y = 3 So our equation is

CATEGORY 5 - $100 No!
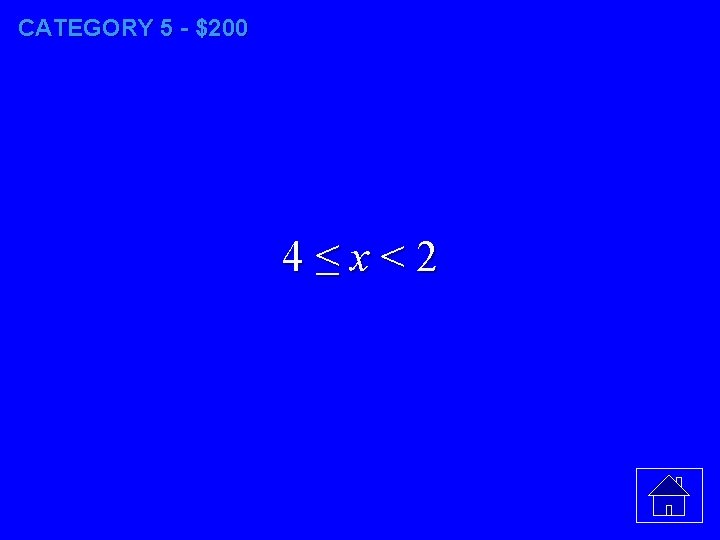
CATEGORY 5 - $200 4≤x<2

CATEGORY 5 - $300 (3 , 2)

CATEGORY 5 - $400 65 Lawns.
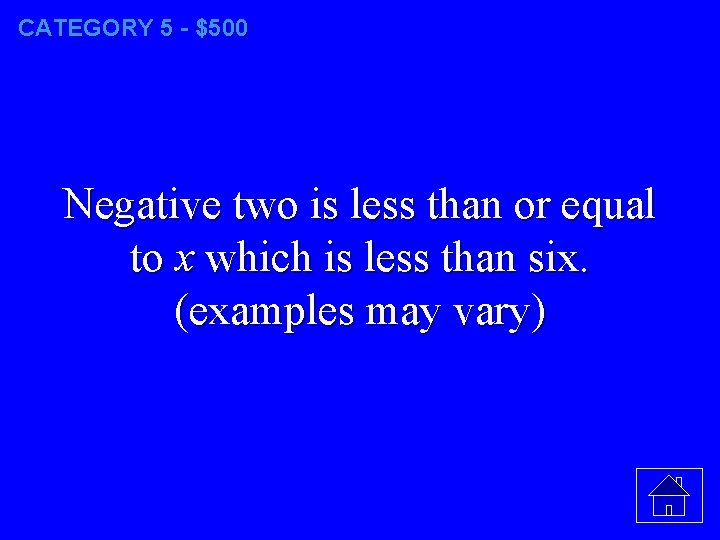
CATEGORY 5 - $500 Negative two is less than or equal to x which is less than six. (examples may vary)
 200 + 200 = 400
200 + 200 = 400 100 + 100 200
100 + 100 200 100 + 100 + 200
100 + 100 + 200 200 200 300
200 200 300 100 100 100 100 100
100 100 100 100 100 100 200 300
100 200 300 100 + 200 + 300 + 400
100 + 200 + 300 + 400 100 200 300 400
100 200 300 400 100 200 300 400
100 200 300 400 100 200 300 400 500
100 200 300 400 500 100+200+300+400
100+200+300+400 300+300+400
300+300+400 200+200+100+100
200+200+100+100 400 + 300 + 300
400 + 300 + 300 300+300+400
300+300+400 300 300 400
300 300 400 300+300+400
300+300+400 300+300+400
300+300+400 300+300+400
300+300+400 300+300+400
300+300+400 200 300 400
200 300 400 200 300 300
200 300 300 200+200+100
200+200+100 400, 200, 100, 50, 25,
400, 200, 100, 50, 25, Testojack 300 review
Testojack 300 review 100+100=200
100+100=200 Who wrote this
Who wrote this Prime factorization jeopardy
Prime factorization jeopardy 200/400 meter training program
200/400 meter training program 120'nin %40 fazlası kaçtır
120'nin %40 fazlası kaçtır Irla levels
Irla levels 106 is prime number
106 is prime number What's 200 * 300
What's 200 * 300 Sometimes between 200-300 b.c
Sometimes between 200-300 b.c The conduction system
The conduction system Wandering atrial pacemaker ecg
Wandering atrial pacemaker ecg Perfect squares between 100 and 200
Perfect squares between 100 and 200 If the interval size is decreased from $200 to $100
If the interval size is decreased from $200 to $100 Qdx=200-2px qsx=-100+4px
Qdx=200-2px qsx=-100+4px Fractions equivalent to 100/200
Fractions equivalent to 100/200 Qdx=200-2px qsx=-100+4px
Qdx=200-2px qsx=-100+4px Box plots gcse
Box plots gcse C/100=f-32/180=k-273/100
C/100=f-32/180=k-273/100 Malloc lab 100/100
Malloc lab 100/100 What's 100 + 100
What's 100 + 100 Héroïne dans la guerre de 100 ans (100 years war).
Héroïne dans la guerre de 100 ans (100 years war). Numeros romanos
Numeros romanos 100 iops/gb and 100,000 iops per volume oci
100 iops/gb and 100,000 iops per volume oci 400 punkte abiturschnitt
400 punkte abiturschnitt Dimensional analysis chemistry definition
Dimensional analysis chemistry definition Ics 400: advanced ics for complex incidents-aberdeen
Ics 400: advanced ics for complex incidents-aberdeen Trotec speedy 400 cena
Trotec speedy 400 cena 350 in scientific notation
350 in scientific notation Atlantik networxx
Atlantik networxx 600+400+500
600+400+500 Dvgw arbeitsblatt w 400-2
Dvgw arbeitsblatt w 400-2 Efavirenz 400 mg vs 600mg
Efavirenz 400 mg vs 600mg 810
810