10 The Interiors of Stars Goals Goals 1





































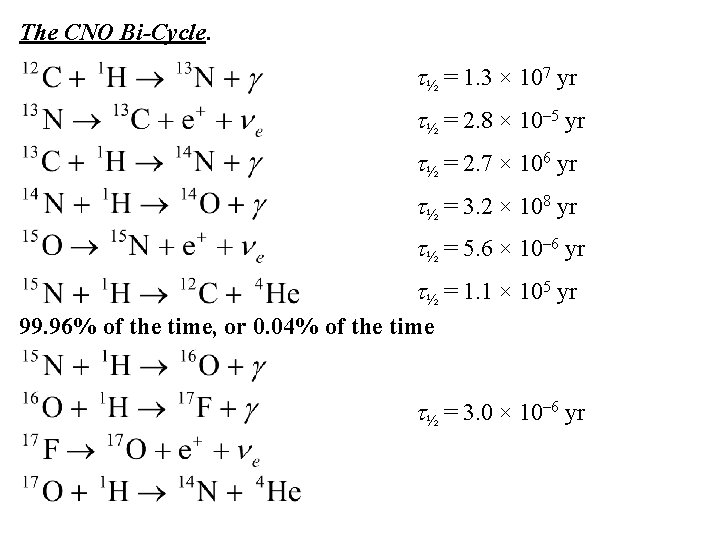














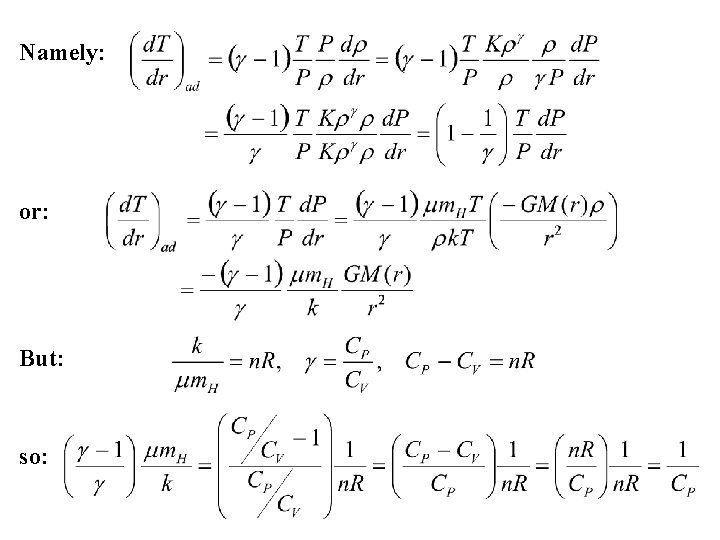













- Slides: 78

10. The Interiors of Stars Goals: Goals 1. Develop the basic equations describing equilibrium conditions applying in stellar interiors. 2. Estimate the physical conditions that must exist at the centre of a typical star, the Sun. 3. Outline potential sources of energy generation in stars and investigate the basics of nuclear reactions as a means of providing a selfsustained energy source. 4. Develop the equations of energy transport in stars.

Fact or Fiction? Consider an inhabited planet completely enshrouded by clouds, upon which astronomy is not a scientific discipline since it is not possible to see into space from the planet’s surface. Yet, one can construct abstract mathematical models of massive spheres of hot gas in equilibrium and deduce their properties from what is known about the physics of matter. Would it come as a surprise to scientists on such a planet if the constant canopy of surrounding clouds one day parted and stars came into view?

Models of Stars The parameters used for studying and modeling stellar interiors include: r = radial distance from the centre of the star M(r) = mass interior to r T(r) = temperature at r P(r) = pressure at r L(r) = luminosity at r ε(r) = energy generation at r κ(r) = opacity at r ρ(r) = density at r In modern models mass M is used as the dependent variable rather than radial distance r, but it is more informative to initiate the study of stellar interiors using the geometrical variable r.

At the “natural” boundaries of the star the corresponding values are: At the centre: r = 0 At the surface: r = R M(r) = 0 M(r) = M* T(r) = Tc T(r) = 0 (or Teff) P(r) = Pc P(r) = 0 L(r) = Lc L(r) = L* ρ(r) = ρc ρ(r) = 0 Rotation and magnetic fields are usually ignored in most models (i. e. spherical symmetry is imposed), as well as any temporal changes (i. e. radial pulsation). Let us examine the equations of stellar structure.

Hydrostatic Equilibrium For balance at any point in the interior of a star, the weight of a block of matter of unit cross-sectional area and thickness dr must be balanced by the buoyancy force of the gas pressure, i. e. : Mass of block = density × volume = ρ dr Weight of the block = mass × local gravity = ρg dr But local gravity, g = GM(r)/r 2 Buoyant Force = pressure difference (top – bottom) = –d. P So:

Example: Obtain a crude estimate for the pressure at the centre of the Sun. Assume 1 M = 1. 9891 × 1033 gm, 1 R = 6. 9598 × 1010 cm and: Solution (instructor): Convert the equation of hydrostatic equilibrium into a difference equation, evaluate it at r = ½R, assume that the mean density and M = ½M* applies there as well. Then: Set d. P = Ps – Pc = 0 – Pc = –Pc and dr = rs – rc = R* – 0 = R*

So, for the Sun: Pc ≈ GM 2/ R 4 = 6. 6726 × 10– 8 × (1. 989 × 1033)2/ (6. 9598 × 1010)4 = 5. 63 × 1015 dynes/cm 2 The textbook method of solution gives a value of: Pc = ~2. 7 × 1015 dynes/cm 2 A more rigorous solution involving integration with the standard solar model gives a more reliable estimate of Pc = 2. 5 × 1017 dynes/cm 2 two orders of magnitude larger! Since 1 atmosphere = 1. 013 × 106 dynes/cm 2, the pressure at the centre of the Sun is equivalent to 2. 5 × 1011 atmospheres!

Conservation of Mass The mass of a star must increase uniformly from the interior to the surface, there cannot be any holes! For each element of thickness dr the volume must increase by the mass of the shell encompassed, i. e. by the spherical area × thickness dr. The resulting equation is:

Ideal Gas Law The ideal gas law is introduced in PHYS 1211: PV = Nk. T, where P is the gas pressure, V its volume, N the number of particles in the volume, T is the temperature (on the absolute scale), and k = 1. 3807 × 10– 16 ergs/K is the Boltzmann constant. It is also expressed using the gas constant R as: PV = n. RT, where n is the number of moles of gas. The relationship can be derived from first principles through the kinetic theory of gases, which specifies that: (i) gas consists of small particles (molecules, atoms) that are smaller than the distances separating them, (ii) particles are in constant motion and make perfectly elastic collisions with container walls, (iii) the motions of particles are random, i. e. ⅓ are moving in any specific direction.

Consider a box of N particles of mass m, where ⅓N are moving in the x-direction. The average force on the right-hand wall (shaded) is given by the rate of change of momentum: Favg = Δ(mv)/Δt A particle takes time Δt to complete a trip from one wall of the box back to the same wall, i. e. Δt = 2 l/v, where l is the dimension of the box. Δ(mv) = mv(before) – mv(after) = mv – (–mv) = 2 mv The resulting pressure (force/unit area) on the shaded wall is given by the total force exerted by all particles in the box on the end wall, i. e. :

But l 3 = V, the volume of the box, so: Since Nm = ρV (density × volume): But the average kinetic energy of a particle ½mv 2 = 3⁄2 k. T, so: The average kinetic energy of a gas molecule at room temperature is:

Pressure Equation of State The ideal gas law is, once again: PV = Nk. T, where P = gas pressure V = volume of the gas N = number of particles in the gas T = temperature (K) k = 1. 3807 × 10– 16 ergs/K is the Boltzmann constant. The number density for the gas can be written as n = N/V, so: P = nk. T, and since the number density can also be written as n = ρ/μm. H, where ρ is the actual density (gm/cm 3), m. H is the mass of a hydrogen atom, and μ is the mean molecular weight. So the gas pressure can be written as:

Mean Molecular Weight As the name implies, the mean molecular weight is the average mass of a gas particle, but in units of the mass of a hydrogen atom, i. e. : where is the average mass of a gas particle. Consider possible examples: Hydrogen: neutral, ionized, molecular,

Helium: neutral, ionized, Heavy element: neutral, ionized, where Aj is the atomic number. In stellar interiors the value of μ for a fully-ionized gas is desired. How does one take into consideration the contributions from all elements?

Let X = fractional abundance by mass of hydrogen, Y = fractional abundance by mass of helium, and Z = fractional abundance by mass of all heavy elements, where X + Y + Z ≡ 1, by definition. In stellar interiors the value of μ for a fully-ionized gas is desired. How does one take into consideration the contributions from all elements? In a cubic centimeter of gas of density ρ there is Xρ of hydrogen, Yρ of helium, and Zρ of heavy elements by mass. Each of the elements contributes different numbers of electrons to the mix, under the assumption of complete ionization: 1 for hydrogen, 2 for helium, and 3, 4, 5… for the heavy elements. The number of particles per cubic centimeter is: Xρ/m. H × 2 = 2 Xρ/m. H for hydrogen Yρ/4 m. H × 3 = 3 Yρ/4 m. H for helium, and Zρ/2 Ajm. H × (Aj + 1) ≈ Zρ/2 m. H for the heavy elements.

The total number of particles per cubic centimeter is therefore given by: So: or: for fully ionized gas, and: for neutral gas, or, since X + Y + Z ≡ 1: When Z is negligible:

Example: What is the mean molecular weight for gas in the Sun, where X = 0. 75, Y = 0. 23, and Z = 0. 02? Solution (instructor): Consider the case for gas that is fully ionized, which gives: i. e. , slightly larger than ½, the value for a pure hydrogen gas.

Example: Obtain an estimate for the temperature at the centre of the Sun. Assume, for simplicity, μi = 0. 5944, i. e. fully-ionized gas. Solution (instructor): We can use the perfect gas law if we know the density at the centre of the Sun. Approximate the value using estimates for conditions at r = ½R (as before), where we assume that ρ =. Assume also that P = ½Pc at that point, that k ≈ 4⁄3 × 10– 16 erg/K, m. H ≈ 3⁄2 × 10– 24 gm, and μi = 0. 5944. Then:

If the average temperature = ½Tc , then Tc = 2. 4 × 107 K, fairly close to the actual value of 1. 6 × 107 K. The central density is found from: whereas the actual value is ~82 gm/cm 3. Since the mass of a hydrogen atom is 1. 6726 × 10– 24 gm, a density of 1. 8 gm/cm 3 corresponds to a number density of n = ρ/μm. H = 1. 81 × 1024 /cm 3. The volume occupied by a particle is 4⁄3πr 3 = 1/n, so the average particle radius is r = 5. 1 × 10– 9 cm = 0. 51 Å, compared with the Bohr radius of 0. 523 Å. With an actual density for the Sun of 82 gm/cm 3, the average particle radius is r = 1. 4 × 10– 9 cm = 0. 14 Å, compared with the Bohr radius of 0. 523 Å. Such highly compressed matter cannot exist as bound atoms, and is referred to as pressure-ionized gas.

Example (from Mechanics): Calculate the gravitational self-energy (energy of assembly piecewise from infinity) of a uniform sphere of mass M and radius R. Solution: Think of assembling the sphere a shell at a time (r = 0 to r = R). For a shell of radius r the incremental potential energy is d. V = φdm, where dm is the mass of the shell and φ is the gravitational potential for the mass already assembled, which is a sphere. Since the mass being assembled forms a spherical shell, we have: So the potential self-energy of the mass is:

where: So the potential self-energy of the sphere is:

Stellar Energy Sources As noted the gravitational potential energy required to contract a star to its present size is given by: But, of the potential energy lost by a star, according to the Virial Theorem (ASTR 2100), one half is transformed into an increase in the kinetic energy of the gas (heat) and the remainder is radiated into space. The radiation lost by a star upon contraction to the main sequence is therefore given by: For the Sun, at its present mass (1. 9891 1033 gm) and radius (6. 9598 1010 cm), the amount of energy radiated through contraction is:

The present luminosity of the Sun is L = 3. 851 1033 ergs/s, so if it had been shining at the same luminosity for the entire duration of its contraction (clearly erroneous) then the time scale for contraction is given by the following: where t. KH is the Kelvin-Helmholtz time scale (more properly the Helmholtz-Kelvin time scale, although it originated with the Scottish physicist John James Waterston, 1811 -1883, whose papers on the subject were rejected by the Royal Society of London!). Here: or ~107 years. The actual value should be smaller because the Sun’s luminosity was greater during the contraction phase, but the main point is that the estimate is much shorter than the estimated age of the solar system of ~4. 6 109 years.

Nuclear Energy Sources Consider the rest masses of the fundamental nuclear particles: Proton: 1. 672623 × 10– 24 gm Neutron: 1. 674929 × 10– 24 gm Electron: 9. 109390 × 10– 28 gm Atomic mass unit, 1 u = 1. 660540 × 10– 24 gm = 931. 49432 Me. V, for E = mc 2. The original nucleon symbolism was: where i. e. , A = mass number = number of nucleons Z = number of protons (usually omitted) X = chemical symbol of the element as specified by Z. is redundant, since indicates the same thing.

Typical masses: 1 H = 1. 007825 u = 938. 78326 Me. V 2 H = 2. 014102 u = 1876. 12457 Me. V 4 He = 4. 002603 u = 3728. 40196 Me. V 5 Li = 5. 0125 u = 4669. 115279 Me. V 8 Be = 8. 005305 u = 7456. 89614 Me. V The major reaction in astronomy converts 4 hydrogen nuclei (protons) into a helium nucleus (4 He). But 4 1 H = 1. 007825 u × 4 and 1 4 He = 4. 002603 u Difference = 4. 031280 u = 4. 002603 u = 0. 028677 u = 0. 0071 of 4 1 H The energy released = mc 2 = 0. 028677 u × 1. 660540 × 10– 24 gm c 2 = 26. 71 Me. V. The lifetime of a star via nuclear reactions depends upon how much of its hydrogen content is converted to energy via nuclear reactions.

For the Sun we can estimate: At L = 3. 851 × 1033 ergs/s, Also, if tnuclear = Enuclear/L* ≈ XM*c 2/M*4 then tnuclear = Xc 2/M*3 ≈ 1010 yrs/(M*/M )3. 1 M , tnuclear = 1010 years 2 M , tnuclear = 109 years (A-star) 4. 6 M , tnuclear = 108 years 10 M , tnuclear = 107 years (B-star) 21. 5 M , tnuclear = 106 years (O-star) 0. 5 M , tnuclear = 1011 years > 1/H 0 (estimated age of the universe) The lifetime of the Sun and stars via nuclear reactions is consistent with the nuclear ages of meteorites, as well as the oldest rocks on the Earth and the Moon.

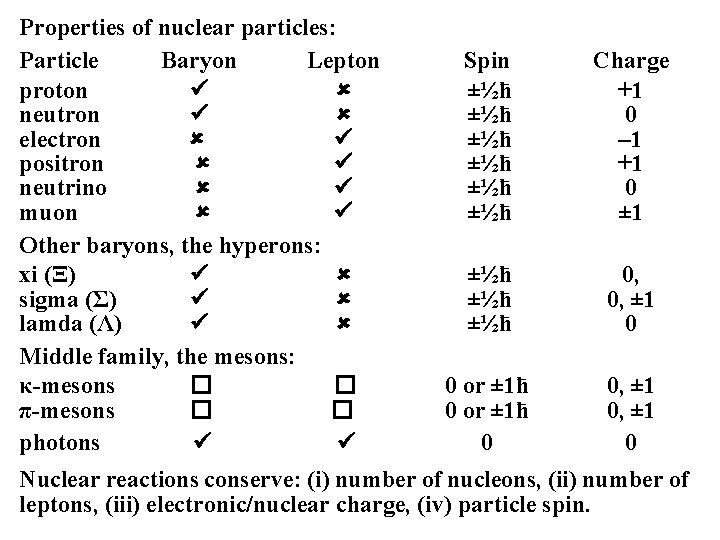
Properties of nuclear particles: Particle Baryon Lepton proton neutron electron positron neutrino muon Other baryons, the hyperons: xi (Ξ) sigma (Σ) lamda (Λ) Middle family, the mesons: κ-mesons � � π-mesons � � photons Spin ±½ћ ±½ћ ±½ћ Charge +1 0 – 1 +1 0 ± 1 ±½ћ ±½ћ 0, 0, ± 1 0 0 or ± 1ћ 0 0, ± 1 0 Nuclear reactions conserve: (i) number of nucleons, (ii) number of leptons, (iii) electronic/nuclear charge, (iv) particle spin.

Example: What is the missing particle in the following reaction? 37 Cl + ν ↔ 37 Ar + ? e The collision of an electron neutrino with a chlorine-37 nucleus produces an argon-37 nucleus plus a to-be-identified particle. Solution: 37 Cl is element 17 with 17 protons, 20 neutrons. 37 Ar is element 18 with 18 protons, 19 neutrons. Nucleons in = 17 + 20 = 37. Nucleons out = 18 + 19 = 37. Leptons in = 1. Leptons out = 0, so missing particle is a lepton. Charge in = +17 (17 protons). Charge out = +18 (18 protons), so missing particle has a charge of – 1. Spin in = 19ћ (17 protons, 20 neutrons, 1 neutrino). Spin out = 18½ћ (18 protons, 19 neutrons), so missing particle has spin ½ћ. The only lepton with spin ½ћ and charge of – 1 is the electron. i. e. , 37 Cl + νe ↔ 37 Ar + e–

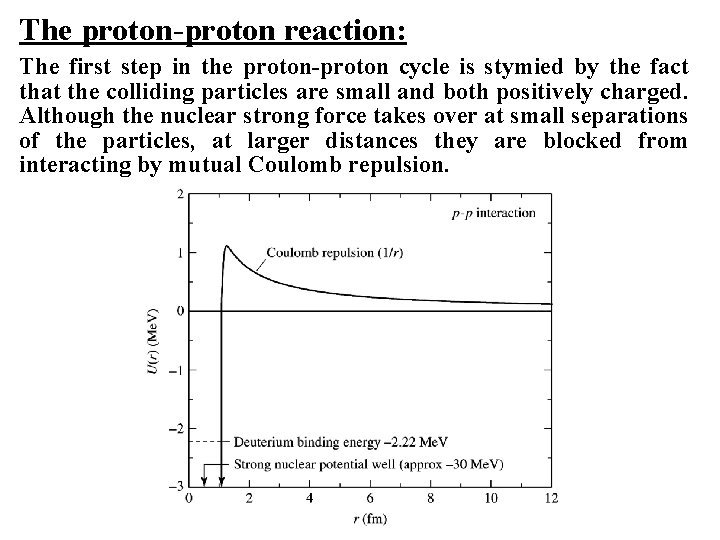
The proton-proton reaction: The first step in the proton-proton cycle is stymied by the fact that the colliding particles are small and both positively charged. Although the nuclear strong force takes over at small separations of the particles, at larger distances they are blocked from interacting by mutual Coulomb repulsion.

How is the Coulomb barrier overcome? Consider the potential energy of a Coulomb barrier: From statistical mechanics we know that kinetic energy and thermal energy are related through the reduced mass of a particle: so: which is much higher than the Sun’s central temperature. But, by the Heisenberg uncertainty principle, the uncertainty in a particle’s momentum, Δpx, is related to the uncertainty in its position, Δx, via: ΔpxΔx ≥ ½ћ = h/4π

Reaction Rates: The rates of individual nuclear reactions depend upon a variety of factors: 1. Atomic nuclei must have sufficient energy to penetrate the Coulomb barrier of the target nucleus, only nuclei with specific energies specified by the high velocity “tail” of the Maxwell. Boltzmann distribution can react with the target nuclei. 2. The cross-section for the reaction, σ(E), must be substantial. The restriction from (1) implies that energetic nuclei capable of reacting with the target nuclei are described by the MB distribution, i. e. , where KE = ½μmv 2 is the kinetic energy of the particle. The restriction from (2) produces:

Denote d. NE as the number of particles of velocity v. E = (2 E/μm)½ that can strike a target nucleus in time dt, i. e. : So: For nx targets/unit volume, the total reaction rate per unit volume per unit time is:

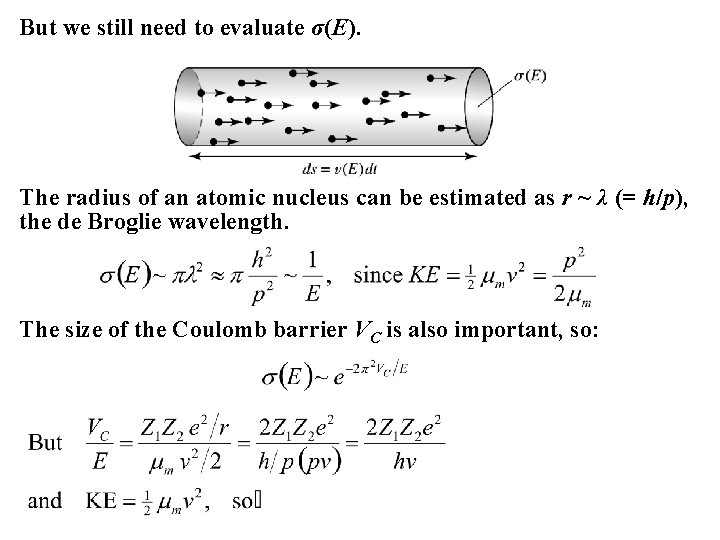
But we still need to evaluate σ(E). The radius of an atomic nucleus can be estimated as r ~ λ (= h/p), the de Broglie wavelength. The size of the Coulomb barrier VC is also important, so:

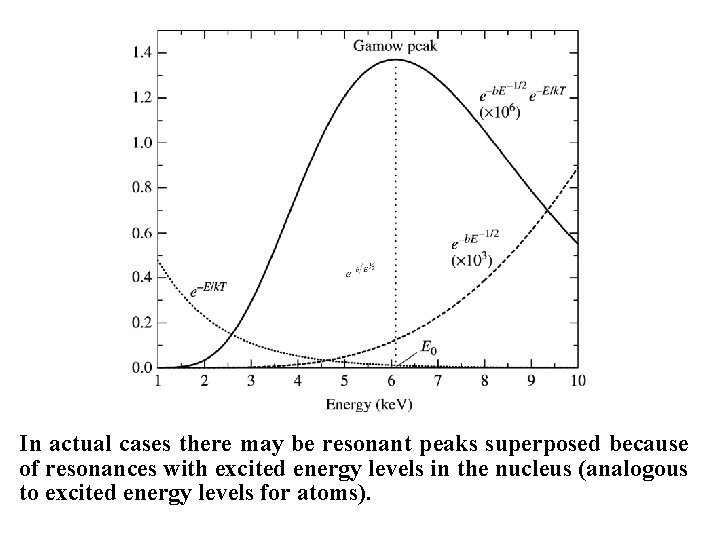
Presumably the function describes the main type of variability, although an additional term that is a slowly varying function of E cannot be excluded. The reaction rate therefore becomes: Where the MB relation has been used as a substitute for n. E. The resulting functional dependence of the reaction rate resembles a Gaussian, and is referred to as the Gamov peak.

In actual cases there may be resonant peaks superposed because of resonances with excited energy levels in the nucleus (analogous to excited energy levels for atoms).

Examples of potential resonant cross-sections in the reaction rate functional dependence.

Electrons can partially shield the positive charges of nuclei, resulting in lower effective Coulomb barriers to reactions, i. e. : where Ves(r) < 0, is the contribution from electron screening. When electron screening is ignored, the integration results in a function that can be approximated as: where r 0 is a constant, Xi is the mass fraction of impacting particles for the reaction, Xx is the mass fraction of target particles for the reaction, and α' and β are exponents established by the integration using a power-law expansion for the reaction rate equations, which have messy integrals.
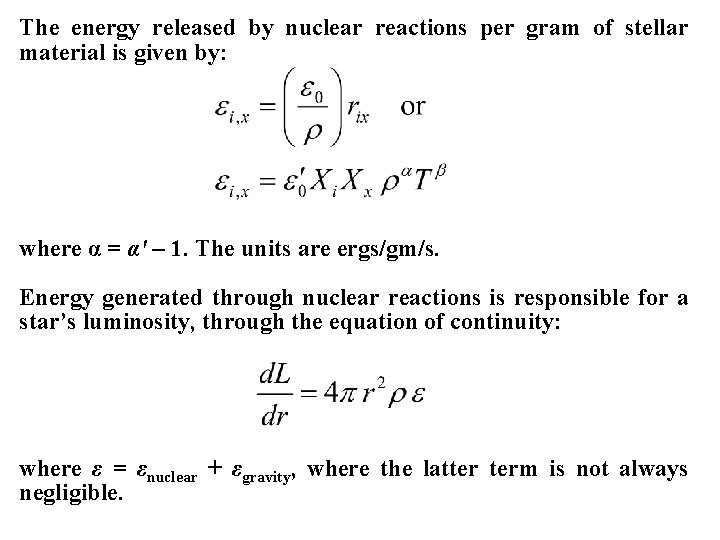
The energy released by nuclear reactions per gram of stellar material is given by: where α = α' – 1. The units are ergs/gm/s. Energy generated through nuclear reactions is responsible for a star’s luminosity, through the equation of continuity: where ε = εnuclear + εgravity, where the latter term is not always negligible.

Nuclear Reaction Chains: All must conserve momentum, energy, spin, charge, etc. : The Proton-Proton Reaction. PPI: (69%) t½ = 7. 9 × 109 yr t½ = 4. 4 × 10– 8 yr t½ = 2. 4 × 105 yr PPII: (30. 85%) t½ = 9. 7 × 105 yr t½ = 3. 9 × 10– 1 yr t½ = 1. 8 × 10– 5 yr

PPIII: (0. 15%) t½ = 9. 7 × 105 yr t½ = 6. 6 × 101 yr instantaneous t½ = 3. 0 × 10– 8 yr Net Reaction: 26. 73 Me. V of energy Energies of Neutrino Products: From 1 H: Maximum Energy = 0. 42 Me. V From 7 Be: Maximum Energy = 0. 86 Me. V From 8 B: Maximum Energy = 14. 0 Me. V


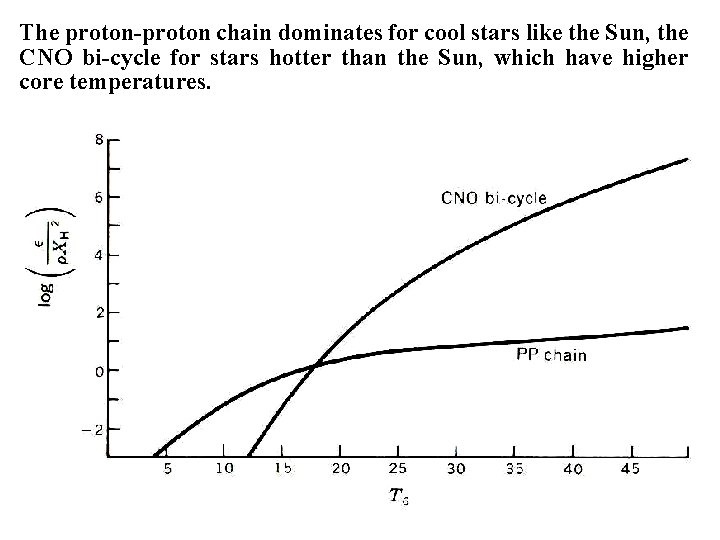
The nuclear energy generation rate for the process can be written as: where T 6 = units of temperature in 106 K, f. PP = f. PP(X, Y, ρ, T) ≈ 1 is the electron screening factor, φPP = φPP(X, Y, T) ≈ 1 is a correction factor to account for the various branches of the PP chain, and c. PP ≈ 1 is a correction factor for higher order terms. In simple form the relationship is written as: for temperatures near 1. 5 107 K. In other words, the energy generation rate for the proton-proton chain varies as the local density and the temperature to the fourth power, ε ~ ρT 4.
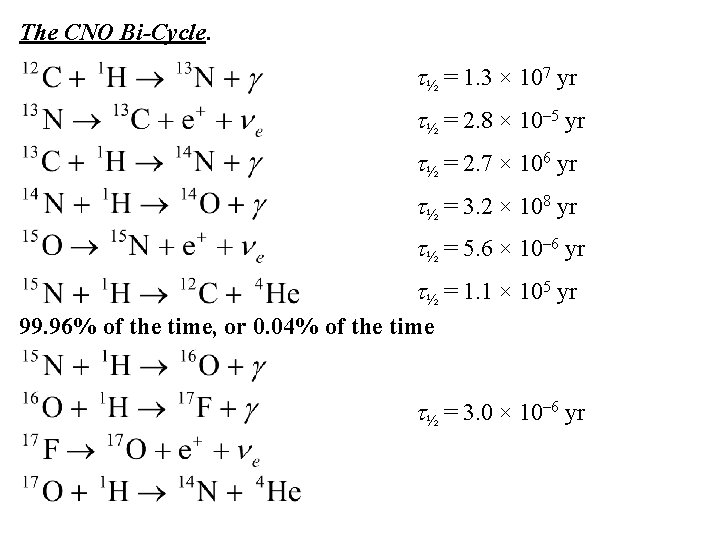
The CNO Bi-Cycle. t½ = 1. 3 × 107 yr t½ = 2. 8 × 10– 5 yr t½ = 2. 7 × 106 yr t½ = 3. 2 × 108 yr t½ = 5. 6 × 10– 6 yr t½ = 1. 1 × 105 yr 99. 96% of the time, or 0. 04% of the time t½ = 3. 0 × 10– 6 yr

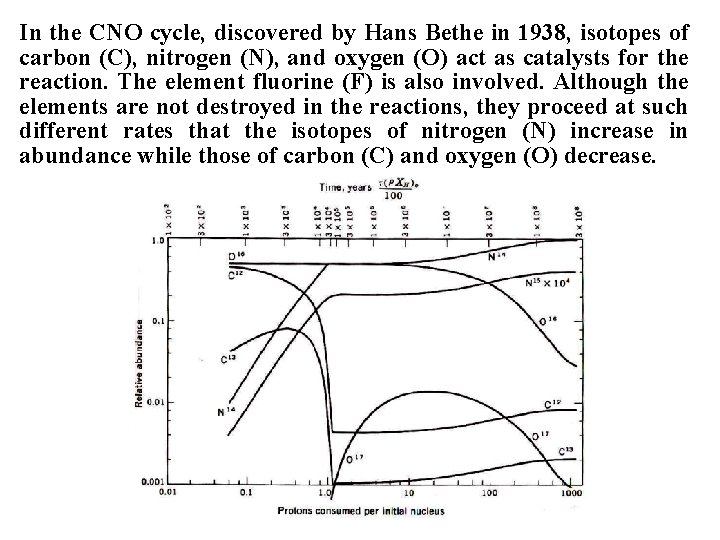
In the CNO cycle, discovered by Hans Bethe in 1938, isotopes of carbon (C), nitrogen (N), and oxygen (O) act as catalysts for the reaction. The element fluorine (F) is also involved. Although the elements are not destroyed in the reactions, they proceed at such different rates that the isotopes of nitrogen (N) increase in abundance while those of carbon (C) and oxygen (O) decrease.

The proton-proton chain dominates for cool stars like the Sun, the CNO bi-cycle for stars hotter than the Sun, which have higher core temperatures.

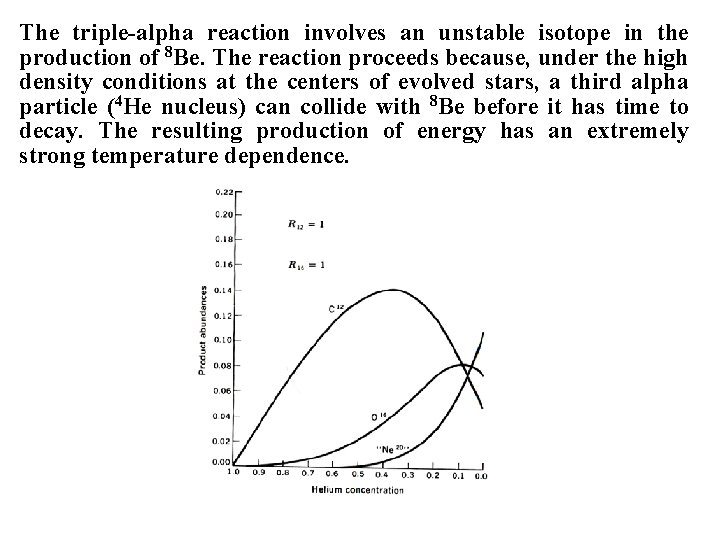
The Triple-Alpha Process. t½ = 1. 3 × 107 yr t½ < 8. 2 × 10– 24 yr Summary: Reaction ρ-dependence X-dependence T-dependence PP Chain ρ1 X 2 T 64 CNO Bi-Cycle ρ1 XXCNO T 619. 9 Triple-Alpha ρ2 Y 3 T 841. 0 Note the higher temperature dependence of the CNO cycle. It is dependent upon the CNO abundances, but dominates over the PP chain for stars somewhat more massive than the Sun where the central temperatures are higher.

The triple-alpha reaction involves an unstable isotope in the production of 8 Be. The reaction proceeds because, under the high density conditions at the centers of evolved stars, a third alpha particle (4 He nucleus) can collide with 8 Be before it has time to decay. The resulting production of energy has an extremely strong temperature dependence.

The Helium Flash. When stellar core material is electron degenerate, the local pressure does not depend upon T. Thus, when He-burning is initiated, the high T-dependence of the 3α process means the energy is generated, raises T locally, thereby increasing the reaction rate, but does not produce a pressure or density decrease to moderate the reaction. The result is known as a helium flash. It only occurs in red giants for stars roughly as massive as the Sun or less, and in more advanced stages of other stars, typically in the white dwarf stage. It is best pictured using the pressure equation: When H-burning or He-burning occurs, the result is a gradual increase in the mean molecular weight μ. If T and ρ remain unchanged, P decreases and unbalances the previously-existing hydrostatic equilibrium. The core of the star collapses so that both P and ρ increase. That enhances the energy generation rate, making the star more luminous. If Teff does not change, the star becomes larger, since L = 4πR 2σTeff 4.

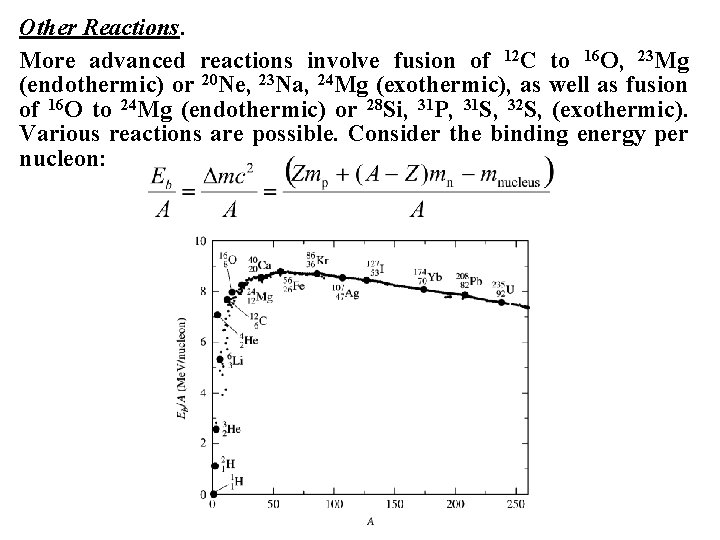
Other Reactions. More advanced reactions involve fusion of 12 C to 16 O, 23 Mg (endothermic) or 20 Ne, 23 Na, 24 Mg (exothermic), as well as fusion of 16 O to 24 Mg (endothermic) or 28 Si, 31 P, 31 S, 32 S, (exothermic). Various reactions are possible. Consider the binding energy per nucleon:

At low atomic weights the most stable nuclei are 1 H, 2 H, 3 He, 6 Li, 4 He, 12 C, 16 O, 24 Mg, 40 Ca, and 56 Fe. At high atomic weights the most stable nuclei are 86 Kr, 107 Ag, 127 I, 174 Yb, 208 Pb, and 238 U. Such unusually stable nuclei are called magic nuclei. The maximum binding energy per nucleus occurs at the iron peak, and all other fusion reactions producing heavier nuclei are endothermic. The problem of explaining the existence of heavy elements in the universe can be restricted to explaining the existence of nuclear reactions that are endothermic in stars. The solution is advanced stages of evolution in massive stars (proton and alpha capture) and supernova explosions (neutron capture).

Energy Transport and Thermodynamics: So far we have developed the following equations of stellar structure: Equation of Continuity: Hydrostatic Equilibrium: Energy Generation: But what about the temperature gradient, d. T/dr?

Radiative Transport: Energy can be transported through a star by radiation, convection, or conduction. Conduction is unimportant in most gaseous stellar interiors, but the other two processes are important. In stellar atmospheres radiative energy transport is described by: But Prad = ⅓a. T 4, so: Thus: But Frad = Lr/4πr 2, giving, for radiative energy transport:

Convective Transport: Convection is a three-dimensional process that must be approximated by one-dimensional equations for simple stellar interior models. It is a process that is difficult to model correctly, but begins with certain assumptions. The pressure scale height HP is defined as: or, if HP = constant, HP is the distance over which the gas pressure P decreases by a factor of 1/e. Example: Estimate a typical value for the pressure scale height in the Sun. Solution: At the midpoint of the Sun we estimated ρ = 4 M /3πR 3. But d. P/dr = –GMρ/r 2 ≈ –GM 2/2 R 5 = –Pc /R. So the pressure scale height can be estimated as: HP = –P/d. P/dr = –½Pc /(–Pc /R ) = ½R More typical values in the Sun are of order HP ≈ 0. 1 R.

Thermodynamics: According to the first law of thermodynamics, the change in internal energy of a mass element, per unit mass, is the difference between the amount of heat added and the work done by the element on its surroundings: d. U = d. Q – d. W. The internal energy of the mass element, U, is: where n. R = k/μm. H is the universal gas constant.

The change in heat of a gaseous mass element is usually expressed in terms of the specific heat C of the gas, where C is the amount of heat required to raise the temperature of a unit mass by 1 K, i. e. : The amount of work done per unit mass by a gas on its surroundings is d. W. The usual expression for work done is: d. W = Pd. V, so d. U = d. Q – Pd. V. When the volume does not change, i. e. , d. V = 0, we have:

But: If the pressure is held constant instead so that the volume changes as heat is added, then: But PV = n. RT, so: and Define: as the ratio of specific heats.

For a monatomic gas: When a gas undergoes ionization, some of the heat d. U that would normally increase the average kinetic energy of the gas is used instead for ionization. The temperature of the gas therefore increases less rapidly so d. T is lower than otherwise. In such instances: so: in such instances. The effect is particularly pronounced in stellar ionization zones.

For adiabatic processes there is no net heat flow into or out of a mass element, so d. Q = 0 and d. U = –d. W = –Pd. V. From PV = n. RT we have: Pd. V + Vd. P = n. Rd. T and d. U = CVd. T, so: From the definition of specific heats we have: so: Pd. V + Vd. P = –(γ– 1)Pd. V

That gives: or: (1+γ– 1)Pd. V = –Vd. P γPd. V = –Vd. P or: The result is the adiabatic gas law: PVγ = K, where K is a constant. But the perfect gas law also gives: PV = n. RT, so:

The sound speed in a gas is related to the incompressibility and inertia of the gas, specifically: For adiabatic sound waves: For convective energy transport one assumes that the gas bubbles are adiabatic. Also the specific volume V = 1/ρ refers to the volume per unit mass. So if P = KV–γ , we must also have P = Kργ.

The formula for the pressure gradient in stellar interiors therefore becomes: With the perfect gas law: so: If there is no gradient in mean molecular weight in a star (not necessarily a valid assumption!), then: from the adiabatic expression for P and ρ. The resulting equation gives an expression for the adiabatic temperature gradient.
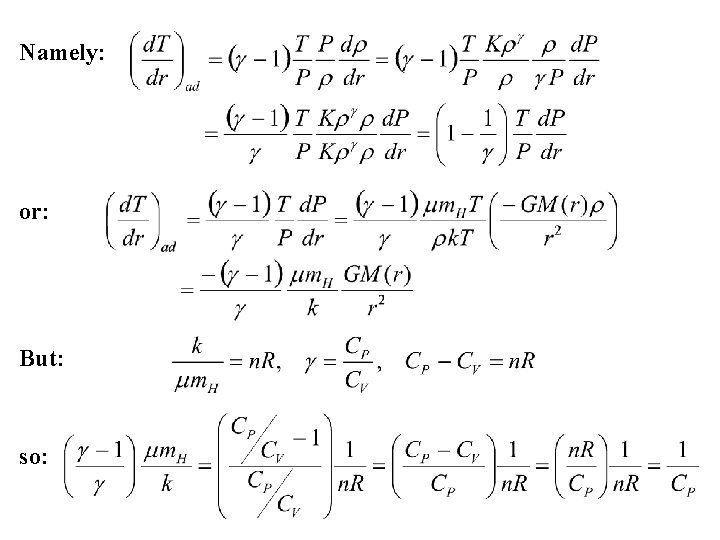
Namely: or: But: so:

The resulting temperature gradient is: If: temperature gradient is superadiabatic. The temperature gradient is a negative quantity since the temperature decreases with increasing radius inside a star. If: heat will be transported by convection. Otherwise the heat is transported outwards by radiation. The deep interiors of stars are relatively simple to understand. They have either convective or radiative cores depending upon the temperature gradient. They may also be semiconvective in the region immediately outside a convective core. Stellar atmospheres are more complicated since heat may be transported by both methods.

The test for whether or not convective or radiative transport describes the temperature gradient inside a star is therefore to test whether or not a displaced bubble of gas rises or falls. It will rise, i. e. convection applies if ρi(bubble) < ρi(surroundings). The condition is: or: See textbook, also for mixing length model.

Stellar Models: The complete set of differential equations describing the interiors of stars is therefore: Equation of Continuity: Hydrostatic Equilibrium: Energy Generation: Temperature Gradient:

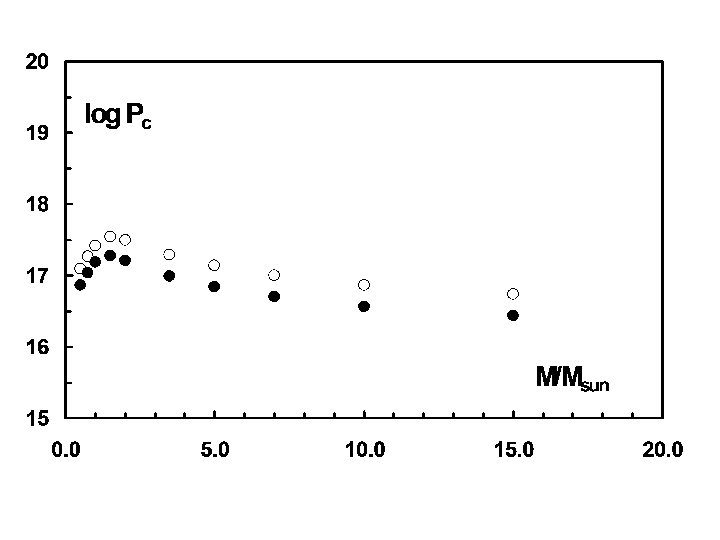
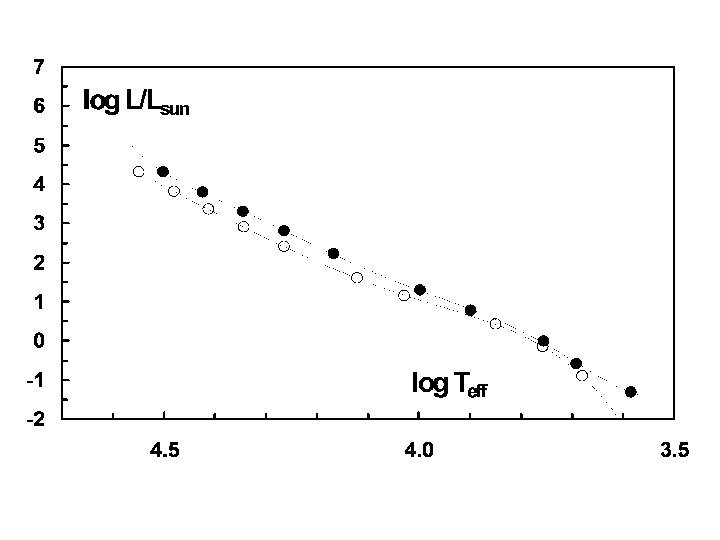
Stellar Models: The results for a series of stellar models at the start of hydrogen burning, i. e. with their initial composition unchanged, is depicted in the following figures. In each case solid circles denote models with a solar metallicity (X = 0. 73, Y = 0. 25, Z = 0. 02), whereas open circles denote models of extremely low metallicity (X = 0. 749, Y = 0. 25, Z = 0. 001). The actual metallicity of the Sun is presently under debate as a result of newer models describing turbulence in the solar atmosphere. Models are constructed numerically using the differential equations as difference equations. They are also rearranged so that the dependent variable is mass rather than radius. Models are then denoted by the number of mass cells they contain. Spherical symmetry is also assumed, although that assumption is relaxed in more recent models.







One of the basic tenets of stellar evolutionary models is the Vogt. Russell Theorem, which states that the mass and chemical composition of a star, and in particular how the chemical composition varies within the star, uniquely determine its radius, luminosity, and internal structure, as well as its subsequent evolution. A consequence of theorem is that it is possible to uniquely describe all of the parameters for a star simply from its location in the Hertzsprung-Russell Diagram. There is no proof for theorem, and in fact, it does fail in some special instances. A prime example of where ambiguities arise occurs when one compares models for two stars, one of which is spherically symmetric and the other of which is flattened as a result of rapid rotation. Both stars can occupy the same location in the Hertzsprung-Russell diagram, at different evolutionary ages and even for different masses.

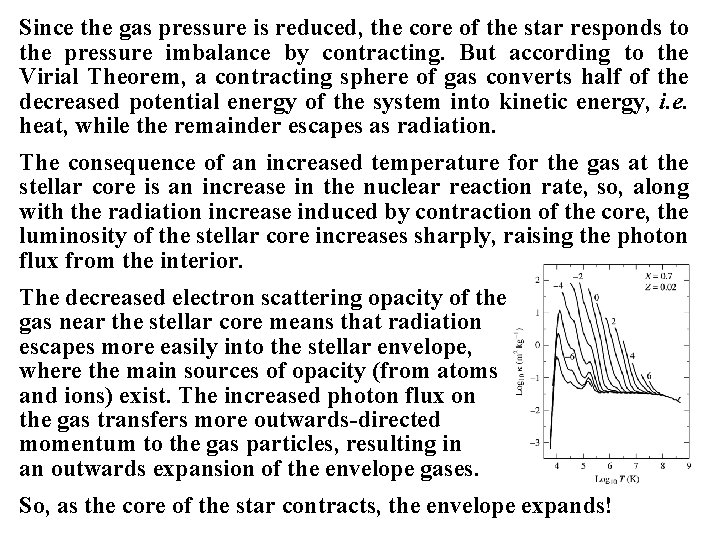
Insights into Stellar Evolution: Consider the sequence of events that happens as stars evolve: During hydrogen burning, the primary 41 H → 4 He reaction converts two protons and two electrons into two neutrons. The reaction chain may suggest that two positrons are produced, but they quickly self-annihilate through collisions with electrons, so the net result is as stated. The production of α-particles from protons and electrons has two effects: (i) the mean molecular weight μ of the gas increases slightly, and (ii) the gas opacity, which is dominated by electron scattering in stellar cores, decreases because of the depleted abundance of electrons. Consequence (i) implies that the gas pressure must decrease, since the mass density of the gas is unaffected. Consequence (ii) implies that radiation escapes the core of the star more easily.

Since the gas pressure is reduced, the core of the star responds to the pressure imbalance by contracting. But according to the Virial Theorem, a contracting sphere of gas converts half of the decreased potential energy of the system into kinetic energy, i. e. heat, while the remainder escapes as radiation. The consequence of an increased temperature for the gas at the stellar core is an increase in the nuclear reaction rate, so, along with the radiation increase induced by contraction of the core, the luminosity of the stellar core increases sharply, raising the photon flux from the interior. The decreased electron scattering opacity of the gas near the stellar core means that radiation escapes more easily into the stellar envelope, where the main sources of opacity (from atoms and ions) exist. The increased photon flux on the gas transfers more outwards-directed momentum to the gas particles, resulting in an outwards expansion of the envelope gases. So, as the core of the star contracts, the envelope expands!

Stellar evolution thus results in an increased luminosity as the star evolves. The resulting change in the effective temperature of the star is more complicated, since increased luminosity can be accommodated by an increase in the stellar radius or an increase in the effective temperature. Since the radius of the star must increase because of envelope expansion, it is not clear what will happen to the star’s effective temperature. Stellar evolutionary models indicate that, for massive stars, the effective temperature decreases as the star evolves. For low mass stars like the Sun, however, the effective temperature actually increases during the initial stages of hydrogen burning. The difference presumably originates from the differences in how energy is transmitted outwards in the two types of stars. Massive stars have convective cores and radiative envelopes, whereas lowmass stars like the Sun have radiative cores and convective envelopes. Convection mixes gas so that any changes in chemical composition are transmitted throughout the convective region, which is clearly more important for high mass stars: M > 1¼ M.

Question. Air is mostly (80%) composed of nitrogen molecules, each of which consists of 28 nucleons (protons and neutrons), where the mass of one nucleon is about one atomic mass unit (1. 6605402 × 10– 24 g). The radius of a typical nitrogen molecule is about 1 Å, and the density of air at sea level is roughly 1. 2 × 10– 3 g cm– 3. Calculate the mean free path for collisions between air molecules under such conditions. The air is at room temperature, i. e. about 300 K, which allows you to estimate the root-meansquared speed, vrms, for air molecules. From that information, calculate the average time between collisions of atoms. Solution: For nitrogen, σ = π(2 r)2 = π(2 × 10– 8)2 cm 2 ≈ π × 4 × 10– 16 cm 2 The number density is n = ρ/m(N 2) = 1. 2 × 10– 3 g cm– 3/(28 × 1. 6605402 × 10– 24 g) = 2. 581 × 1019 cm– 3 So the mean free path is l = 1/nσλ = 1/(2. 581 × 1019 × π × 4 × 10– 16 ) ≈ 3 × 10– 5 cm v. RMS = (3 k. T/m)½ = (3 × 1. 38 × 10– 16 × 300/4. 65 × 10– 23)½ ≈ 5. 17 × 104 cm/s The average time between collisions is t = l/v = (1. 25 × 10– 4 cm)/(5. 17 × 104 cm/s) ≈ 2 × 10– 9 s

Question. According to a “standard model” for the Sun, the central density is 162 g cm– 3 and the Rosseland mean opacity κ is 1. 16 cm 2 g– 1. a. Calculate the mean free path for a photon at the centre of the Sun. b. If the mean free path remains constant for the photon’s journey to the surface of the Sun, how long, on average, would it take for photons to escape from the Sun? Solution: The mean free path for a photon is l = 1/κλρ = 1/(1. 16 × 162) ≈ 5 × 10– 3 cm The distance traveled by a photon between collisions is d 2 = Nl 2 In order to escape from the Sun a photon has to travel a distance of 6. 9598 × 1010 cm Number of collisions is N = d 2/l 2 = (6. 9598 × 1010)2/(5 × 10– 3)2 = 1. 9376 × 1026, each taking t = l/c = 5 × 10– 3 cm/3 × 1010 cm/s = 1. 7 × 10– 13 s Time to escape the Sun is Nt = 1. 9376 × 1026 × 1. 7 × 10– 13 s) = 3. 23 × 1013 s ≈ 106 years
 Palladian interior design
Palladian interior design Amrut aakar interior
Amrut aakar interior There are three sizes of schnauzer dog
There are three sizes of schnauzer dog Strategic goals tactical goals operational goals
Strategic goals tactical goals operational goals Strategic goals tactical goals operational goals
Strategic goals tactical goals operational goals General goals and specific goals
General goals and specific goals Examples of generic goals and product-specific goals
Examples of generic goals and product-specific goals đặc điểm cơ thể của người tối cổ
đặc điểm cơ thể của người tối cổ Tỉ lệ cơ thể trẻ em
Tỉ lệ cơ thể trẻ em Phối cảnh
Phối cảnh Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Thế nào là hệ số cao nhất
Thế nào là hệ số cao nhất ưu thế lai là gì
ưu thế lai là gì Sơ đồ cơ thể người
Sơ đồ cơ thể người Môn thể thao bắt đầu bằng từ đua
Môn thể thao bắt đầu bằng từ đua Tư thế ngồi viết
Tư thế ngồi viết Hình ảnh bộ gõ cơ thể búng tay
Hình ảnh bộ gõ cơ thể búng tay Cái miệng bé xinh thế chỉ nói điều hay thôi
Cái miệng bé xinh thế chỉ nói điều hay thôi Mật thư anh em như thể tay chân
Mật thư anh em như thể tay chân Tư thế ngồi viết
Tư thế ngồi viết Chó sói
Chó sói Thẻ vin
Thẻ vin Thơ thất ngôn tứ tuyệt đường luật
Thơ thất ngôn tứ tuyệt đường luật Các châu lục và đại dương trên thế giới
Các châu lục và đại dương trên thế giới Sự nuôi và dạy con của hươu
Sự nuôi và dạy con của hươu Từ ngữ thể hiện lòng nhân hậu
Từ ngữ thể hiện lòng nhân hậu Diễn thế sinh thái là
Diễn thế sinh thái là Lp html
Lp html V. c c
V. c c Vẽ hình chiếu vuông góc của vật thể sau
Vẽ hình chiếu vuông góc của vật thể sau 101012 bằng
101012 bằng Lời thề hippocrates
Lời thề hippocrates Tư thế worms-breton
Tư thế worms-breton đại từ thay thế
đại từ thay thế Quá trình desamine hóa có thể tạo ra
Quá trình desamine hóa có thể tạo ra Công của trọng lực
Công của trọng lực Thế nào là mạng điện lắp đặt kiểu nổi
Thế nào là mạng điện lắp đặt kiểu nổi Dạng đột biến một nhiễm là
Dạng đột biến một nhiễm là Thế nào là sự mỏi cơ
Thế nào là sự mỏi cơ Bổ thể
Bổ thể Vẽ hình chiếu đứng bằng cạnh của vật thể
Vẽ hình chiếu đứng bằng cạnh của vật thể độ dài liên kết
độ dài liên kết Thiếu nhi thế giới liên hoan
Thiếu nhi thế giới liên hoan Khi nào hổ con có thể sống độc lập
Khi nào hổ con có thể sống độc lập điện thế nghỉ
điện thế nghỉ Chúa sống lại
Chúa sống lại Một số thể thơ truyền thống
Một số thể thơ truyền thống Trời xanh đây là của chúng ta thể thơ
Trời xanh đây là của chúng ta thể thơ Số nguyên tố là
Số nguyên tố là Fault in our stars
Fault in our stars Characters setting plot conflict climax theme
Characters setting plot conflict climax theme Night
Night Edwin hubble
Edwin hubble Number the stars chapter 17
Number the stars chapter 17 Stars were gleaming shepherds dreaming
Stars were gleaming shepherds dreaming Shakespeare doubt
Shakespeare doubt Chapter 19 section 2 the life cycle of stars answer key
Chapter 19 section 2 the life cycle of stars answer key Shooting stars analysis
Shooting stars analysis Life cycle of a star poster
Life cycle of a star poster Magnitude scale stars
Magnitude scale stars Flowering and non flowering plants
Flowering and non flowering plants Midnight stars make bright the skies
Midnight stars make bright the skies What is the life cycle of a star
What is the life cycle of a star What is the interstellar medium
What is the interstellar medium When i look up to the stars believe
When i look up to the stars believe Stars citizens lone wolves apathetics
Stars citizens lone wolves apathetics Cepheid variable stars
Cepheid variable stars Characteristics of stars diagram
Characteristics of stars diagram Fusion inside stars
Fusion inside stars Stars raffelt
Stars raffelt Star with small and medium mass
Star with small and medium mass Body symmetry of echinoderms
Body symmetry of echinoderms Pascal's identity proof
Pascal's identity proof The stars and i chapter 19
The stars and i chapter 19 What is parallax method
What is parallax method Stars
Stars O silent night the stars are brightly shining
O silent night the stars are brightly shining Sun and rigel
Sun and rigel Dancing the stars
Dancing the stars