10 th lecture Frictional flow in a constant

10 th lecture Frictional flow in a constant area duct preceded by an isentropic nozzle (convergent nozzle, convergent divergent nozzle)

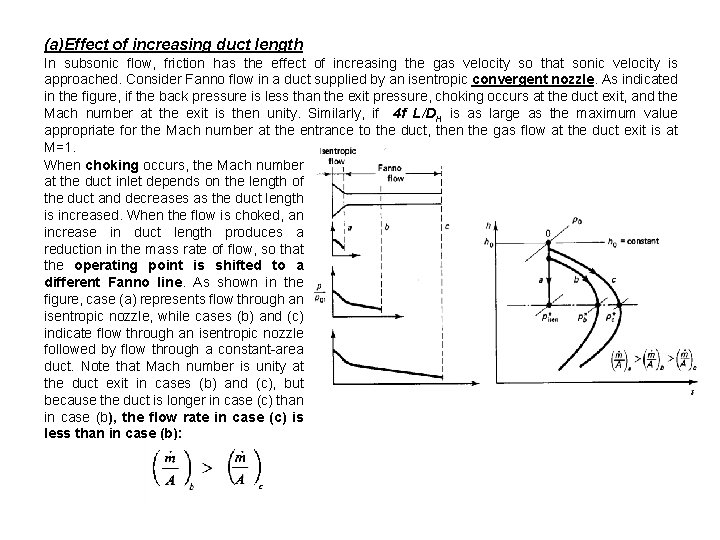
(a)Effect of increasing duct length In subsonic flow, friction has the effect of increasing the gas velocity so that sonic velocity is approached. Consider Fanno flow in a duct supplied by an isentropic convergent nozzle. As indicated in the figure, if the back pressure is less than the exit pressure, choking occurs at the duct exit, and the Mach number at the exit is then unity. Similarly, if 4 f L/DH is as large as the maximum value appropriate for the Mach number at the entrance to the duct, then the gas flow at the duct exit is at M=1. When choking occurs, the Mach number at the duct inlet depends on the length of the duct and decreases as the duct length is increased. When the flow is choked, an increase in duct length produces a reduction in the mass rate of flow, so that the operating point is shifted to a different Fanno line. As shown in the figure, case (a) represents flow through an isentropic nozzle, while cases (b) and (c) indicate flow through an isentropic nozzle followed by flow through a constant-area duct. Note that Mach number is unity at the duct exit in cases (b) and (c), but because the duct is longer in case (c) than in case (b), the flow rate in case (c) is less than in case (b):

In the case were gas flowing supersonically enters a duct, there is a reduction in the velocity and an increase in the pressure of the gas. The gas velocity approaches sonic conditions; however, subsonic conditions can also be attained if a discontinuity occurs. If the length of the duct exceeds the maximum value prescribed by the Mach number at the entrance to the duct, a shock appears in the duct. The shock will position itself in the duct to cause a sonic condition at duct exit. If the duct length is increased further, the shock will position itself further upstream. If the duct is very long, the shock will be at the throat of the nozzle. Beyond that length, there will be no shock at all, and the flow is subsonic at all points. Further increases in duct length cause a reduction in flow rate. (b) Effect of reducing back pressure (i) Flow through convergent nozzle followed by a constant-area duct As shown in the figure, the velocity is subsonic through. In this case, the length of the duct is maintained constant but the back pressure is successively lowered. The gas expands isentropically in the nozzle and continues to expand in the duct along a Fanno line, until the back pressure pa is reached. Flow in both the nozzle and duct accelerates continuously, and the exit pressure is equal to the back pressure. When the back pressure is lowered to pb, the exit pressure also becomes reduced so that the exit pressure coincides with the back pressure.

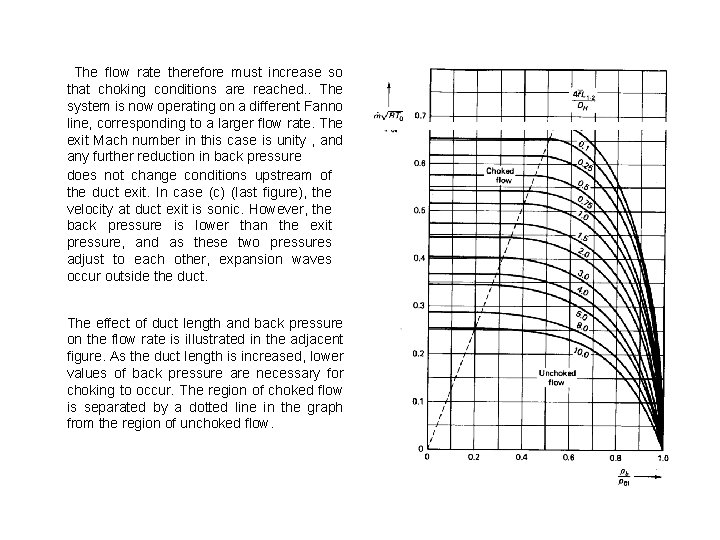
The flow rate therefore must increase so that choking conditions are reached. . The system is now operating on a different Fanno line, corresponding to a larger flow rate. The exit Mach number in this case is unity , and any further reduction in back pressure does not change conditions upstream of the duct exit. In case (c) (last figure), the velocity at duct exit is sonic. However, the back pressure is lower than the exit pressure, and as these two pressures adjust to each other, expansion waves occur outside the duct. The effect of duct length and back pressure on the flow rate is illustrated in the adjacent figure. As the duct length is increased, lower values of back pressure are necessary for choking to occur. The region of choked flow is separated by a dotted line in the graph from the region of unchoked flow.

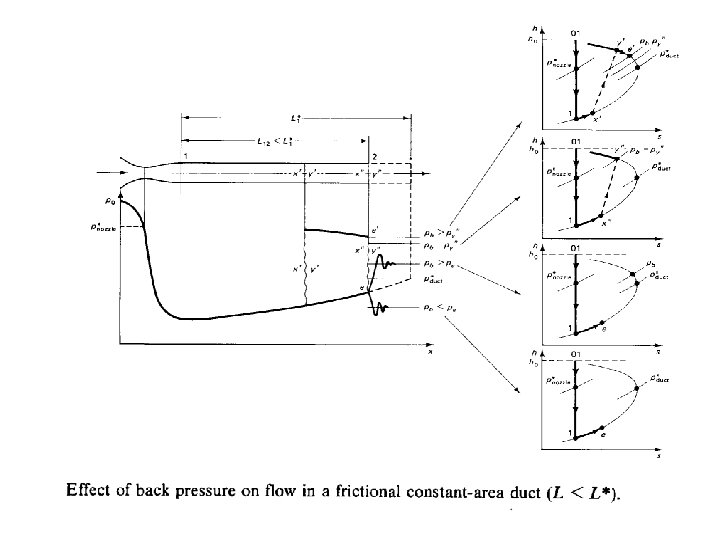
(ii) Flow through convergent-divergent nozzle followed by a constant-area duct In case of supersonic flow, both Mach number and gas properties at the entrance to the duct are determined by ratio of duct area to throat area. As long as the flow is choked at the throat of the nozzle, changes in duct length cdo not affect the mass rate of flow, and there exists a maximum length of duct appropriate for the Mach number at the duct inlet. The effect of raising the back pressure will be considered for the two different cases: (a) L L* and (b) L L*, where L and L* refer to two ducts that are geometrically identical except that L* is the duct length which corresponds to sonic velocity at the exit. (I) L L* • Referring to the next figure, consider the nozzle-duct system, where the duct length is less than L*. Let pe be the exit pressure for shockless flow. When the back pressure is below py" but above pe , the flow in the duct is entirely supersonic and the pressure at the exit from the duct is less than the back pressure. Adjustments in pressure occur in the form of oblique shocks beyond the exit from the duct. If the back pressure is lower than pe (and pe is lower than p*duct), then oblique expansion waves form at the duct exit. It is possible for normal shock to form at the exit of the duct. In that case, py", the downstream pressure of the shock, is exactly equal to the back pressure. When the back pressure is larger than py", the shock occurs within the duct, even though the length of a duct, L, is less than L*, the maximum specified for shockless flow. The pressure distribution in a duct as the back pressure increases is shown in the figure found in the next slide.

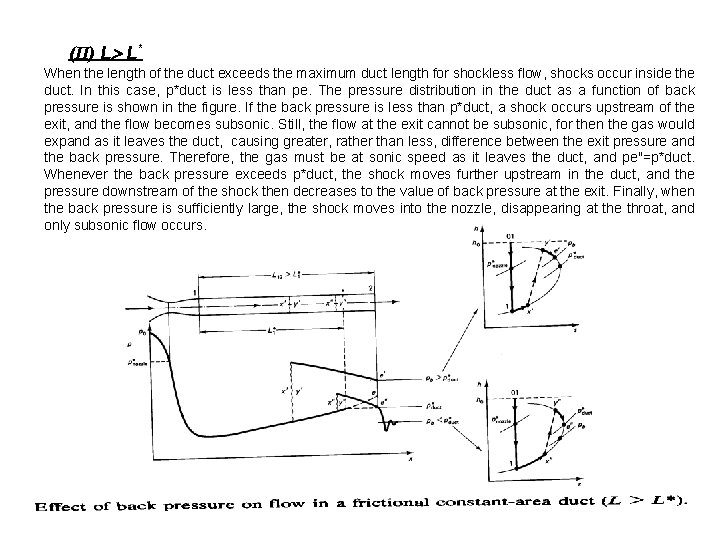
(II) L L* When the length of the duct exceeds the maximum duct length for shockless flow, shocks occur inside the duct. In this case, p*duct is less than pe. The pressure distribution in the duct as a function of back pressure is shown in the figure. If the back pressure is less than p*duct, a shock occurs upstream of the exit, and the flow becomes subsonic. Still, the flow at the exit cannot be subsonic, for then the gas would expand as it leaves the duct, causing greater, rather than less, difference between the exit pressure and the back pressure. Therefore, the gas must be at sonic speed as it leaves the duct, and pe"=p*duct. Whenever the back pressure exceeds p*duct, the shock moves further upstream in the duct, and the pressure downstream of the shock then decreases to the value of back pressure at the exit. Finally, when the back pressure is sufficiently large, the shock moves into the nozzle, disappearing at the throat, and only subsonic flow occurs.