10 TH EDITION COLLEGE ALGEBRA LIAL HORNSBY SCHNEIDER

10 TH EDITION COLLEGE ALGEBRA LIAL HORNSBY SCHNEIDER 1. 4 - 1

1. 4 Quadratic Equations Solving a Quadratic Equation Completing the Square The Quadratic Formula Solving for a Specified Variable The Discriminant 1. 4 - 2 1. 1

Quadratic Equation in One Variable An equation that can be written in the form where a, b, and c are real numbers with a ≠ 0, is a quadratic equation. The given form is called standard form. 1. 4 - 3

Second-degree Equation A quadratic equation is a second-degree equation. This is an equation with a squared variable term and no terms of greater degree. 1. 4 - 4

Zero-Factor Property If a and b are complex numbers with ab = 0, then a = 0 or both. 1. 4 - 5

Example 1 USING THE ZERO-FACTOR PROPERTY Solve Solution: Standard form Factor. Zero-factor property. 1. 4 - 6

Example 1 USING THE ZERO-FACTOR PROPERTY Solve Solution: Zero-factor property. Solve each equation. 1. 4 - 7

Square-Root Property A quadratic equation of the form x 2 = k can also be solved by factoring Subtract k. Factor. Zero-factor property. Solve each equation. 1. 4 - 8

Square Root Property If x 2 = k, then 1. 4 - 9

Square-Root Property That is, the solution of Both solutions are real if k > 0, and both are imaginary if k < 0 If k < 0, we write the solution set as If k = 0, then this is sometimes called a double solution. 1. 4 - 10

Example 2 USING THE SQUARE ROOT PROPERTY Solve each quadratic equation. a. Solution: By the square root property, the solution set is 1. 4 - 11

USING THE SQUARE ROOT PROPERTY Example 2 Solve each quadratic equation. b. Solution: Since the solution set of x 2 = − 25 is 1. 4 - 12

Example 2 USING THE SQUARE ROOT PROPERTY Solve each quadratic equation. c. Solution: Use a generalization of the square root property. Generalized square root property. Add 4. 1. 4 - 13

Solving A Quadratic Equation By Completing The Square To solve ax 2 + bx + c = 0, by completing the square: Step 1 If a ≠ 1, divide both sides of the equation by a. Step 2 Rewrite the equation so that the constant term is alone on one side of the equality symbol. Step 3 Square half the coefficient of x, and add this square to both sides of the equation. Step 4 Factor the resulting trinomial as a perfect square and combine like terms on the other side. Step 5 Use the square root property to complete the solution. 1. 4 - 14

Example 3 USING THE METHOD OF COMPLETING THE SQUARE a = 1 Solve x 2 – 4 x – 14 = 0 by completing the square. Solution Step 1 This step is not necessary since a = 1. Step 2 Add 14 to both sides. Step 3 add 4 to both sides. Step 4 Factor; combine terms. 1. 4 - 15

Example 3 USING THE METHOD OF COMPLETING THE SQUARE a = 1 Solve x 2 – 4 x – 14 = 0 by completing the square. Solution Step 4 Factor; combine terms. Step 5 Square root property. Take both roots. Add 2. Simplify the radical. The solution set is 1. 4 - 16

Example 4 USING THE METHOD OF COMPLETING THE SQUARE a ≠ 1 Solve 9 x 2 – 12 x + 9 = 0 by completing the square. Solution Divide by 9. (Step 1) Add – 1. (Step 2) 1. 4 - 17

Example 4 USING THE METHOD OF COMPLETING THE SQUARE a = 1 Solve 9 x 2 – 12 x + 9 = 0 by completing the square. Solution Factor, combine terms. (Step 4) Square root property 1. 4 - 18

Example 4 USING THE METHOD OF COMPLETING THE SQUARE a = 1 Solve 9 x 2 – 12 x + 9 = 0 by completing the square. Solution Square root property Quotient rule for radicals Add ⅔. 1. 4 - 19

Example 4 USING THE METHOD OF COMPLETING THE SQUARE a = 1 Solve 9 x 2 – 12 x + 9 = 0 by completing the square. Solution Add ⅔. The solution set is 1. 4 - 20

The Quadratic Formula The method of completing the square can be used to solve any quadratic equation. If we start with the general quadratic equation, ax 2 + bx + c = 0, a ≠ 0, and complete the square to solve this equation for x in terms of the constants a, b, and c, the result is a general formula for solving any quadratic equation. We assume that a > 0. 1. 4 - 21

Quadratic Formula The solutions of the quadratic equation ax 2 + bx + c = 0, where a ≠ 0, are 1. 4 - 22

Caution Notice that the fraction bar in the quadratic formula extends under the – b term in the numerator. 1. 4 - 23

Example 5 USING THE QUADRATIC FORMULA (REAL SOLUTIONS) Solve x 2 – 4 x = – 2 Solution: Write in standard form. Here a = 1, b = – 4, c = 2 Quadratic formula. 1. 4 - 24

Example 5 USING THE QUADRATIC FORMULA (REAL SOLUTIONS) Solve x 2 – 4 x = – 2 Solution: Quadratic formula. The fraction bar extends under – b. 1. 4 - 25

Example 5 USING THE QUADRATIC FORMULA (REAL SOLUTIONS) Solve x 2 – 4 x = – 2 Solution: The fraction bar extends under – b. 1. 4 - 26

Example 5 USING THE QUADRATIC FORMULA (REAL SOLUTIONS) Solve x 2 – 4 x = – 2 Solution: Factor out 2 in the numerator. Factor first, then divide. Lowest terms. The solution set is 1. 4 - 27

Example 6 USING THE QUADRATIC FORMULA (NONREAL COMPLEX SOLUTIONS) Solve 2 x 2 = x – 4. Solution: Write in standard form. Quadratic formula; a = 2, b = – 1, c = 4 Use parentheses and substitute carefully to avoid errors. 1. 4 - 28

Example 6 USING THE QUADRATIC FORMULA (NONREAL COMPLEX SOLUTIONS) Solve 2 x 2 = x – 4. Solution: The solution set is 1. 4 - 29

Cubic Equation The equation x 3 + 8 = 0 that follows is called a cubic equation because of the degree 3 term. Some higher-degree equations can be solved using factoring and the quadratic formula. 1. 4 - 30

Example 7 SOLVING A CUBIC EQUATION Solve Solution Factor as a sum of cubes. or Zero-factor property or Quadratic formula; a = 1, b = – 2, c = 4 1. 4 - 31

Example 7 SOLVING A CUBIC EQUATION Solve Solution Simplify the radical. Factor out 2 in the numerator. 1. 4 - 32

Example 7 SOLVING A CUBIC EQUATION Solve Solution Lowest terms 1. 4 - 33

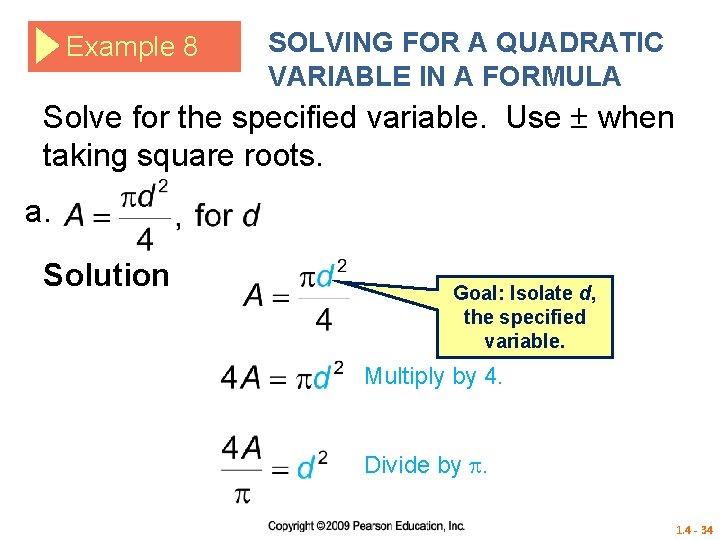
Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve for the specified variable. Use when taking square roots. a. Solution Goal: Isolate d, the specified variable. Multiply by 4. Divide by . 1. 4 - 34

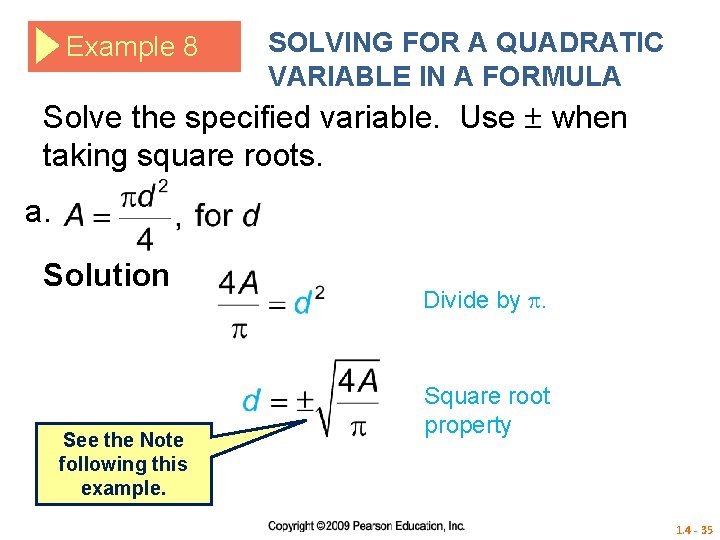
Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. a. Solution See the Note following this example. Divide by . Square root property 1. 4 - 35

Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. a. Solution Square root property Rationalize the denominator. 1. 4 - 36

Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. a. Solution Rationalize the denominator. Multiply numerators; multiply denominators. 1. 4 - 37

Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. a. Solution Multiply numerators; multiply denominators. Simplify. 1. 4 - 38

Solving for a Specified Variable Note In Example 8, we took both positive and negative square roots. However, if the variable represents a distance or length in an application, we would consider only the positive square root. 1. 4 - 39

Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. b. Solution Write in standard form. Now use the quadratic formula to find t. 1. 4 - 40

Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. b. Solution a = r, b = – s, and c = – k 1. 4 - 41

Example 8 SOLVING FOR A QUADRATIC VARIABLE IN A FORMULA Solve the specified variable. Use when taking square roots. b. Solution a = r, b = – s, and c = –k Simplify. 1. 4 - 42

The Discriminant The quantity under the radical in the quadratic formula, b 2 – 4 ac, is called the discriminant. Discriminant 1. 4 - 43

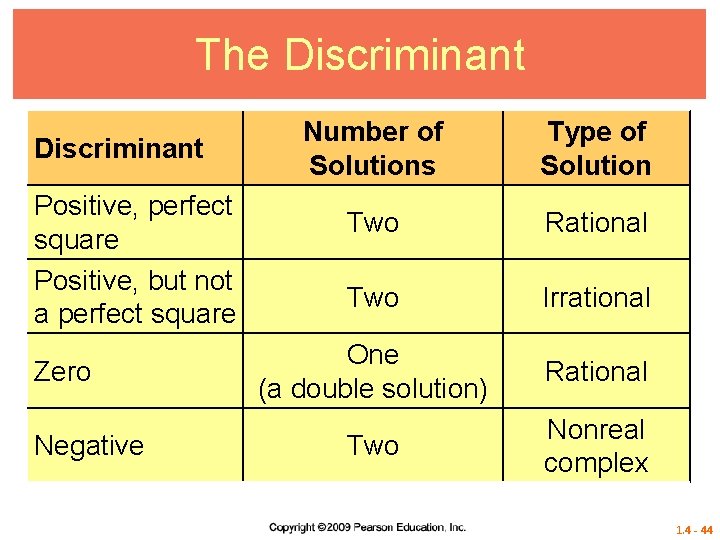
The Discriminant Positive, perfect square Positive, but not a perfect square Zero Negative Number of Solutions Type of Solution Two Rational Two Irrational One (a double solution) Rational Two Nonreal complex 1. 4 - 44

Caution The restriction on a, b, and c is important. For example, for the equation the discriminant is b 2 – 4 ac = 5 + 4 = 9, which would indicate two rational solutions if the coefficients were integers. By the quadratic formula, however, the two solutions are irrational numbers, 1. 4 - 45

Example 9 USING THE DISCRIMINANT Determine the number of distinct solutions, and tell whether they are rational, irrational, or nonreal complex numbers. a. Solution For 5 x 2 + 2 x – 4 = 0, a = 5, b = 2, and c = – 4. The discriminant is b 2 – 4 ac = 22 – 4(5)(– 4) = 84 The discriminant is positive and not a perfect square, so there are two distinct irrational solutions. 1. 4 - 46

Example 9 USING THE DISCRIMINANT Determine the number of distinct solutions, and tell whether they are rational, irrational, or nonreal complex numbers. b. Solution First write the equation in standard form as x 2 – 10 x + 25 = 0. Thus, a = 1, b = – 10, and c = 25, and b 2 – 4 ac =(– 10 )2 – 4(1)(25) = 0 There is one distinct rational solution, a “double solution. ” 1. 4 - 47

Example 9 USING THE DISCRIMINANT Determine the number of distinct solutions, and tell whether they are rational, irrational, or nonreal complex numbers. c. Solution For 2 x 2 – x + 1 = 0, a = 2, b = – 1, and c = 1, so b 2 – 4 ac = (– 1)2 – 4(2)(1) = – 7. There are two distinct nonreal complex solutions. (They are complex conjugates. ) 1. 4 - 48