10 Statistical Inference for Two Samples CHAPTER OUTLINE

Learning Objectives for Chapter 10 After careful study of this chapter, you should be

10 -1: Introduction 3 © John Wiley & Sons, Inc. Applied Statistics and Probability

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown

10 -4: Paired t-Test • A special case of the two-sample t-tests of Section

10 -4: Paired t-Test The Paired t-Test 46 © John Wiley & Sons, Inc.

10 -4: Paired t-Test Example 10 -10 47 © John Wiley & Sons, Inc.

10 -4: Paired t-Test Example 10 -10 48 © John Wiley & Sons, Inc.

10 -4: Paired t-Test Example 10 -10 49 © John Wiley & Sons, Inc.

10 -4: Paired t-Test Paired Versus Unpaired Comparisons 50 © John Wiley & Sons,

10 -4: Paired t-Test A Confidence Interval for D Definition 51 © John Wiley

10 -4: Paired t-Test Example 10 -11 52 © John Wiley & Sons, Inc.

10 -4: Paired t-Test Example 10 -11 53 © John Wiley & Sons, Inc.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 1 The

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 2 Hypothesis

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -12 60

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -12 61

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -12 62

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 3 Type

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -13 64

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 4 Confidence

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -14 66

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -14 67

10 -6: Inference on Two Population Proportions 10 -6. 1 Large-Sample Test on the

10 -6: Inference on Two Population Proportions Example 10 -15 71 © John Wiley

10 -6: Inference on Two Population Proportions Example 10 -15 72 © John Wiley

10 -6: Inference on Two Population Proportions Example 10 -15 73 © John Wiley

10 -6: Inference on Two Population Proportions Minitab Output for Example 10 -15 74

10 -6: Inference on Two Population Proportions 10 -6. 2 Type II Error and

10 -6: Inference on Two Population Proportions 10 -6. 3 Confidence Interval on the

10 -6: Inference on Two Population Proportions Example 10 -16 79 © John Wiley

10 -6: Inference on Two Population Proportions Example 10 -16 80 © John Wiley

10 -7: Summary Table and Road Map for Inference Procedures for Two Samples Table

Important Terms & Concepts of Chapter 10 Paired t-test Comparative experiments Pooled t-test Confidence

Slides: 83

Download presentation

10 Statistical Inference for Two Samples CHAPTER OUTLINE 10 -1 Inference on the Difference in Means of Two 10 -5 Inference on the Variances of Two Normal Distributions, Variances Known Populations 10 -1. 1 Hypothesis tests on the difference of means, 10 -5. 1 F distributions variances known 10 -5. 2 Hypothesis tests on the ratio of two variances 10 -1. 2 Type II error and choice of sample size 10 -5. 3 Type II error and choice of sample size 10 -1. 3 Confidence interval on the difference in means, 10 -5. 4 Confidence interval on the ratio of two variances variance known 10 -2 Inference on the Difference in Means of Two 10 -6 Inference on Two Population Proportions Normal Distributions, Variance Unknown 10 -6. 1 Large sample tests on the difference in 10 -2. 1 Hypothesis tests on the difference of means, variances unknown 10 -2. 2 Type II error and choice of sample size 10 -2. 3 Confidence interval on the difference in means, variance unknown population proportions 10 -6. 2 Type II error and choice of sample size 10 -6. 3 Confidence interval on the difference in population proportions 10 -7 Summary Table and Roadmap for Inference 10 -3 A Nonparametric Test on the Difference of Procedures for Two Samples Two Means 10 -4 Paired t-Tests 1

Learning Objectives for Chapter 10 After careful study of this chapter, you should be able to do the following: 1. Structure comparative experiments involving two samples as hypothesis tests. 2. Test hypotheses and construct confidence intervals on the difference in means of two normal distributions. 3. Test hypotheses and construct confidence intervals on the ratio of the variances or standard deviations of two normal distributions. 4. Test hypotheses and construct confidence intervals on the difference in two population proportions. 5. Use the P-value approach for making decisions in hypothesis tests. 6. Compute power, Type II error probability, and make sample size decisions for two-sample tests on means, variances & proportions. 7. Explain & use the relationship between confidence intervals and hypothesis tests. 2 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -1: Introduction 3 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

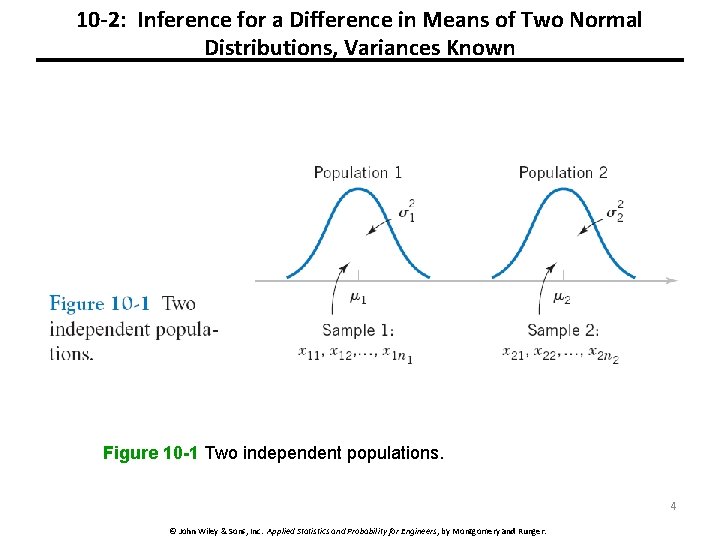
10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Figure 10 -1 Two independent populations. 4 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Assumptions 5 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known 6 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known 10 -2. 1 Hypothesis Tests for a Difference in Means, Variances Known 7 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Example 10 -1 8 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Example 10 -1 9 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Example 10 -1 10 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known 10 -2. 2 Type II Error and Choice of Sample Size Use of Operating Characteristic Curves Two-sided alternative: One-sided alternative: 11 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known 10 -2. 2 Type II Error and Choice of Sample Size Formulas Two-sided alternative: 12 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known 10 -2. 2 Type II Error and Choice of Sample Size Formulas One-sided alternative: 13 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Example 10 -3 14 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known 10 -2. 3 Confidence Interval on a Difference in Means, Variances Known Definition 15 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Example 10 -4 16 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Example 10 -4 17 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known Choice of Sample Size 18 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -2: Inference for a Difference in Means of Two Normal Distributions, Variances Known One-Sided Confidence Bounds Upper Confidence Bound Lower Confidence Bound 19 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 1 Hypotheses Tests for a Difference in Means, Variances Unknown Case 1: We wish to test: 20 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 1 Hypotheses Tests for a Difference in Means, Variances Unknown Case 1: The pooled estimator of 2: 21 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 1 Hypotheses Tests for a Difference in Means, Variances Unknown Case 1: 22 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Definition: The Two-Sample or Pooled t-Test* 23 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

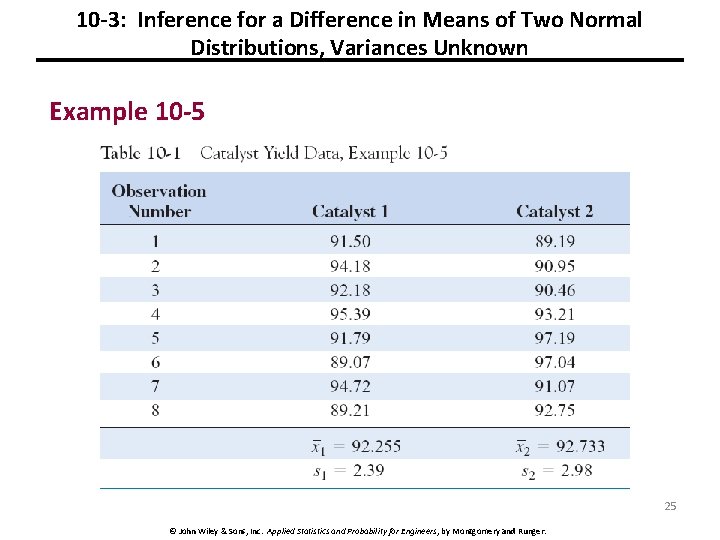
10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -5 24 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -5 25 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -5 26 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -5 27 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Minitab Output for Example 10 -5 28 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

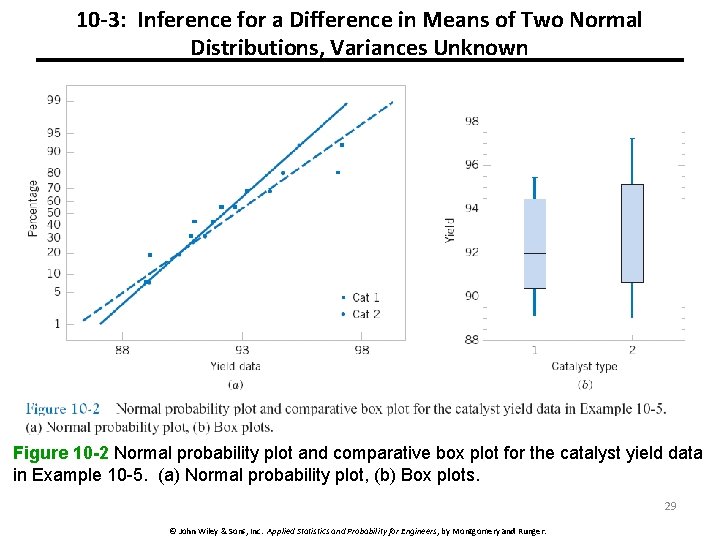
10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Figure 10 -2 Normal probability plot and comparative box plot for the catalyst yield data in Example 10 -5. (a) Normal probability plot, (b) Box plots. 29 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 1 Hypotheses Tests for a Difference in Means, Variances Unknown Case 2: is distributed approximately as t with degrees of freedom given by 30 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 1 Hypotheses Tests for a Difference in Means, Variances Unknown Case 2: 31 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -6 32 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -6 (Continued) 33 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -6 (Continued) 34 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

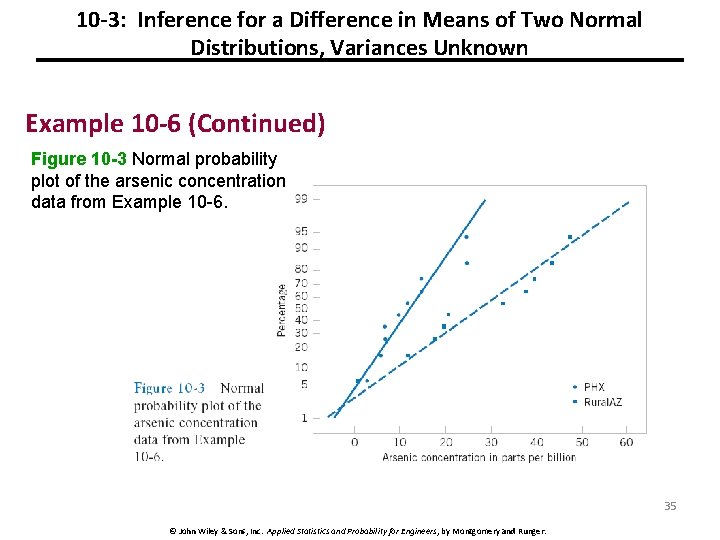
10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -6 (Continued) Figure 10 -3 Normal probability plot of the arsenic concentration data from Example 10 -6. 35 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Example 10 -6 (Continued) 36 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 2 Type II Error and Choice of Sample Size Example 10 -7 37 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Minitab Output for Example 10 -7 38 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 3 Confidence Interval on the Difference in Means, Variance Unknown Case 1: 39 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Case 1: Example 10 -8 40 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Case 1: Example 10 -8 (Continued) 41 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Case 1: Example 10 -8 (Continued) 42 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown Case 1: Example 10 -8 (Continued) 43 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -3: Inference for a Difference in Means of Two Normal Distributions, Variances Unknown 10 -3. 3 Confidence Interval on the Difference in Means, Variance Unknown Case 2: 44 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test • A special case of the two-sample t-tests of Section 10 -3 occurs when the observations on the two populations of interest are collected in pairs. • Each pair of observations, say (X 1 j , X 2 j ), is taken under homogeneous conditions, but these conditions may change from one pair to another. • The test procedure consists of analyzing the differences between hardness readings on each specimen. 45 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test The Paired t-Test 46 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test Example 10 -10 47 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test Example 10 -10 48 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test Example 10 -10 49 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test Paired Versus Unpaired Comparisons 50 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test A Confidence Interval for D Definition 51 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

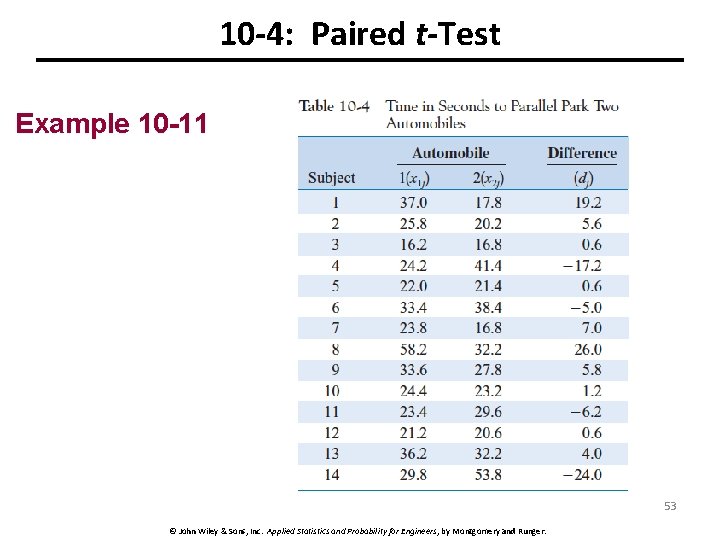
10 -4: Paired t-Test Example 10 -11 52 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -4: Paired t-Test Example 10 -11 53 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

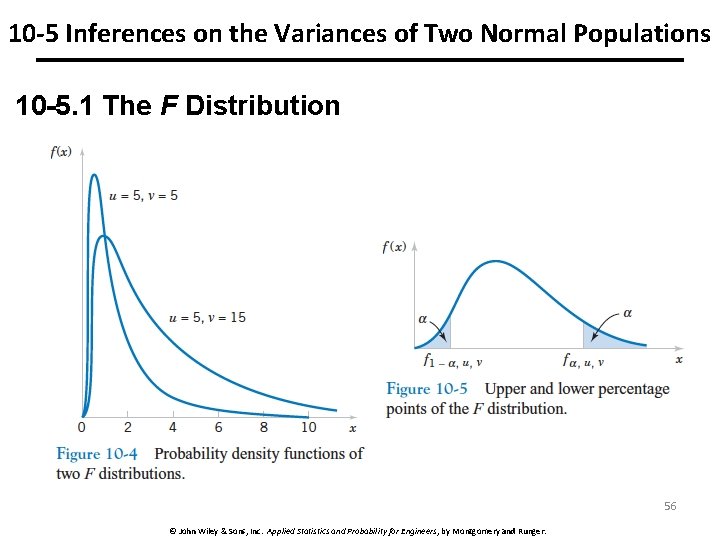
10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 1 The F Distribution We wish to test the hypotheses: • The development of a test procedure for these hypotheses requires a new probability distribution, the F distribution. 54 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 1 The F Distribution 55 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 1 The F Distribution 56 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 1 The F Distribution The lower-tail percentage points f -1, u, can be found as follows. 57 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 2 Hypothesis Tests on the Ratio of Two Variances 58 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 2 Hypothesis Tests on the Ratio of Two Variances 59 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -12 60 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -12 61 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -12 62 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 3 Type II Error and Choice of Sample Size 63 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -13 64 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations 10 -5. 4 Confidence Interval on the Ratio of Two Variances 65 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -14 66 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -5 Inferences on the Variances of Two Normal Populations Example 10 -14 67 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 1 Large-Sample Test on the Difference in Population Proportions We wish to test the hypotheses: 68 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 1 Large-Sample Test on the Difference in Population Proportions The following test statistic is distributed approximately as standard normal and is the basis of the test: 69 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 1 Large-Sample Test on the Difference in Population Proportions 70 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions Example 10 -15 71 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions Example 10 -15 72 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions Example 10 -15 73 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions Minitab Output for Example 10 -15 74 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 2 Type II Error and Choice of Sample Size 75 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 2 Type II Error and Choice of Sample Size 76 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 2 Type II Error and Choice of Sample Size 77 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions 10 -6. 3 Confidence Interval on the Difference in the Population Proportions 78 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions Example 10 -16 79 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

10 -6: Inference on Two Population Proportions Example 10 -16 80 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

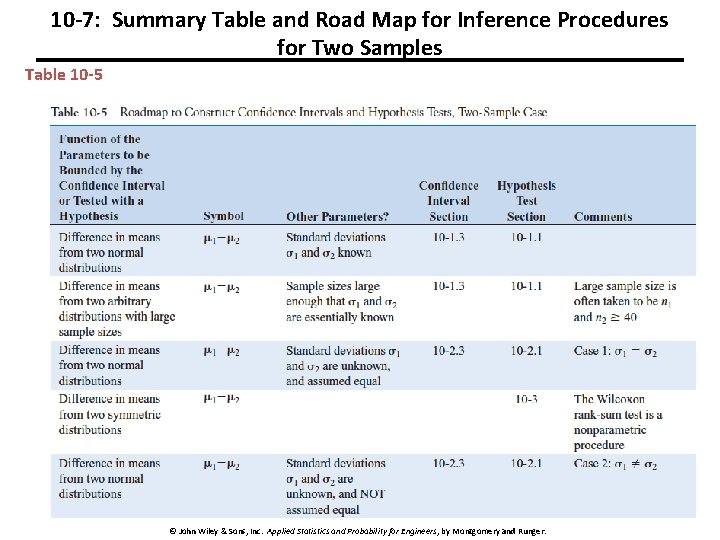
10 -7: Summary Table and Road Map for Inference Procedures for Two Samples Table 10 -5 81 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

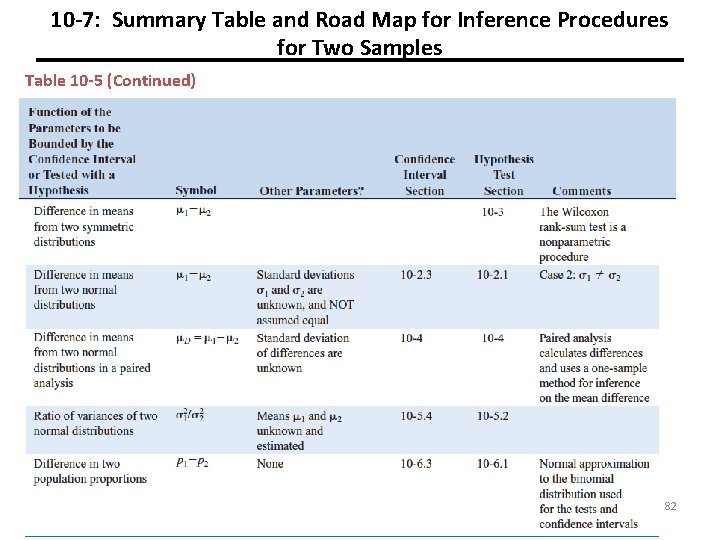
10 -7: Summary Table and Road Map for Inference Procedures for Two Samples Table 10 -5 (Continued) 82 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.

Important Terms & Concepts of Chapter 10 Paired t-test Comparative experiments Pooled t-test Confidence intervals on: P-value • Differences • Ratios Reference distribution for a test Critical region for a test statistic Sample size determination for: Identifying cause and effect Null and alternative hypotheses Hypothesis tests Confidence intervals 1 & 2 -sided alternative Statistical hypotheses Operating Characteristic (OC) Test statistic curves Wilcoxon rank-sum test 83 © John Wiley & Sons, Inc. Applied Statistics and Probability for Engineers, by Montgomery and Runger.