10 Schwingungen sind allgemein Vorgnge die sich wiederholen

10. Schwingungen sind allgemein Vorgänge, die sich wiederholen. Man spricht auch oft von periodischen Vorgängen. Beispiele: Vibrationen, Pendelschwingung, . . . 10. 1. Harmonische Schwingungen Versuch: 10. Schwingungen

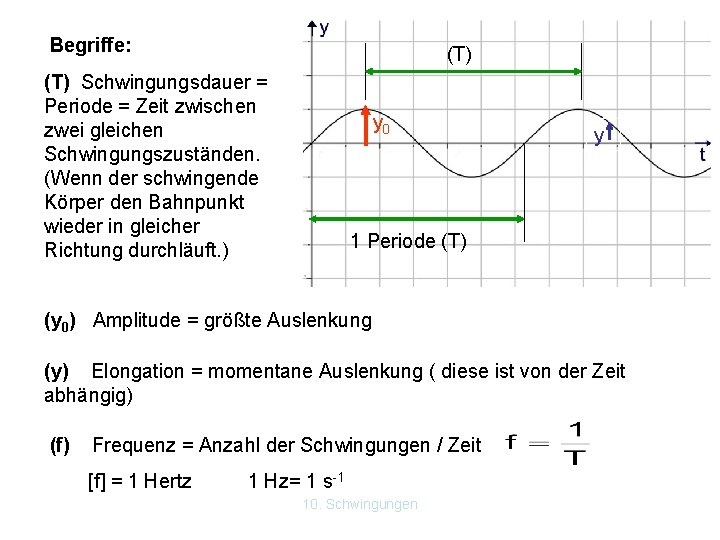
Begriffe: (T) Schwingungsdauer = Periode = Zeit zwischen zwei gleichen Schwingungszuständen. (Wenn der schwingende Körper den Bahnpunkt wieder in gleicher Richtung durchläuft. ) y 0 y 1 Periode (T) (y 0) Amplitude = größte Auslenkung (y) Elongation = momentane Auslenkung ( diese ist von der Zeit abhängig) (f) Frequenz = Anzahl der Schwingungen / Zeit [f] = 1 Hertz 1 Hz= 1 s-1 10. Schwingungen

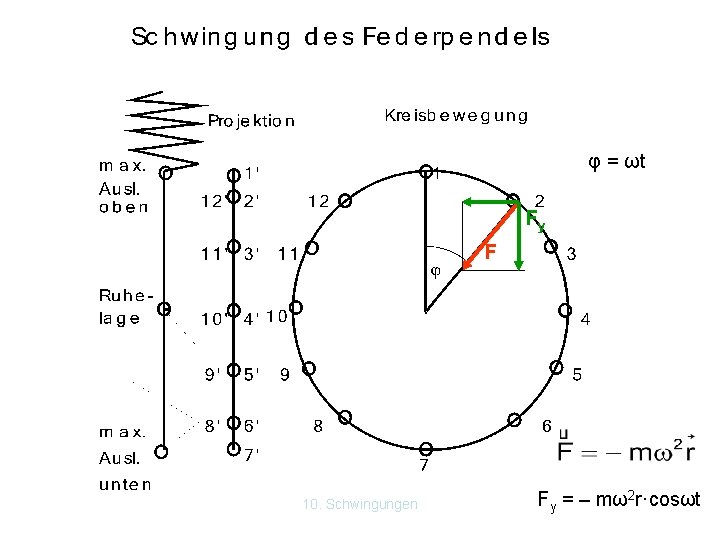
Beispiele für harmonische Schwingungen: 10. 1. 1 Schwingung des Federpendels: Wir vergleichen die Projektion einer Kreisbewegung mit der Schwingung eines Federpendels. Federpendel: Kreisbewegung u. deren Projektion Fy = – k·y - weil F, y antiparallel Fy = – ky 0·cosωt φ = ωt Fy = – mω2 r·cosωt Fy = – m ω2 y 0 cosωt 10. Schwingungen k y r = y 0

φ = ωt Fy F 10. Schwingungen Fy = – mω2 r·cosωt

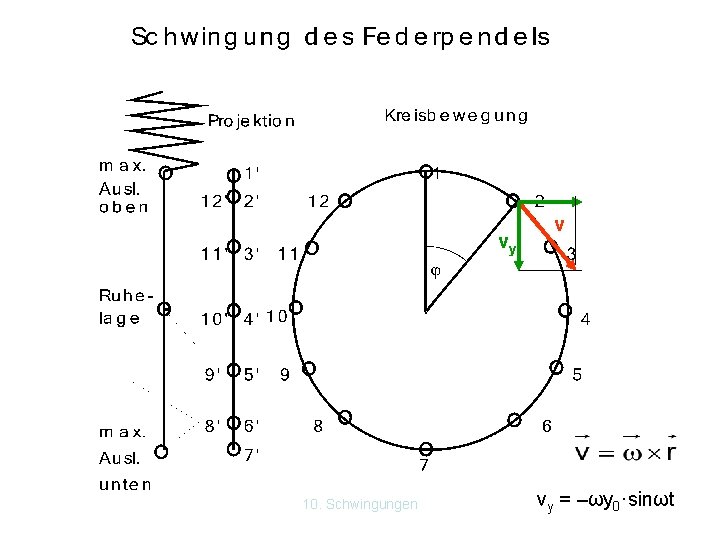
vy 10. Schwingungen v vy = –ωy 0·sinωt

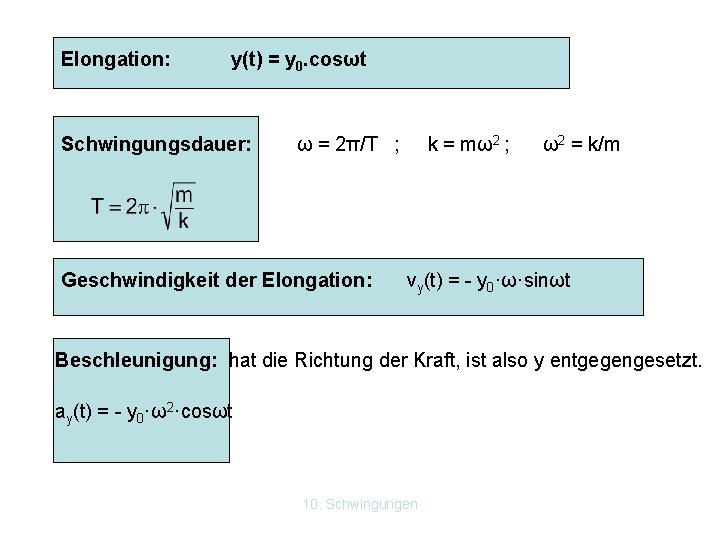
Elongation: y(t) = y 0. cosωt Schwingungsdauer: ω = 2π/T ; Geschwindigkeit der Elongation: k = mω2 ; ω2 = k/m vy(t) = - y 0·ω·sinωt Beschleunigung: hat die Richtung der Kraft, ist also y entgegengesetzt. ay(t) = - y 0·ω2·cosωt 10. Schwingungen

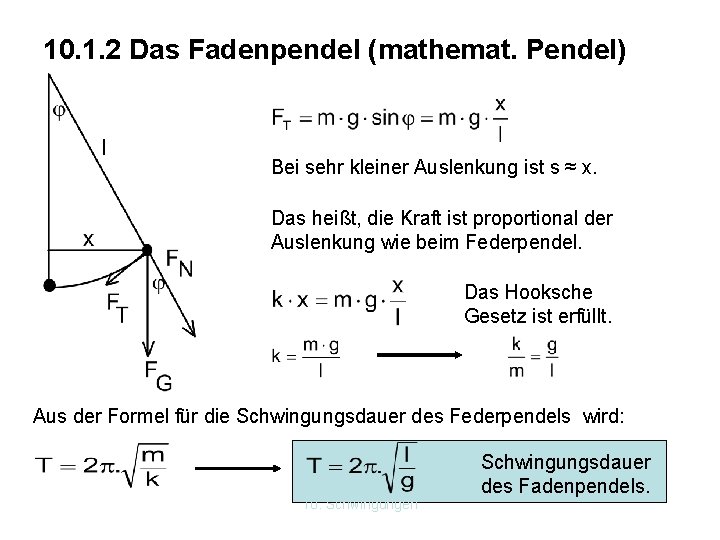
10. 1. 2 Das Fadenpendel (mathemat. Pendel) Bei sehr kleiner Auslenkung ist s ≈ x. Das heißt, die Kraft ist proportional der Auslenkung wie beim Federpendel. Das Hooksche Gesetz ist erfüllt. Aus der Formel für die Schwingungsdauer des Federpendels wird: 10. Schwingungen Schwingungsdauer des Fadenpendels.

Schülerversuche zu Feder- und Fadenpendel 10. Schwingungen

Federpendel • Aufbau: 10. Schwingungen

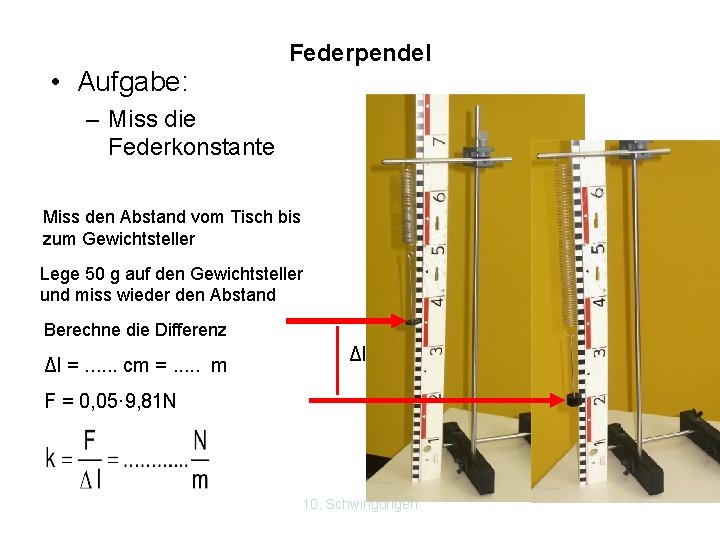
• Aufgabe: Federpendel – Miss die Federkonstante Miss den Abstand vom Tisch bis zum Gewichtsteller Lege 50 g auf den Gewichtsteller und miss wieder den Abstand Berechne die Differenz Δl =. . . cm =. . . m Δl F = 0, 05· 9, 81 N 10. Schwingungen

Federpendel • Aufgabe: – Miss die Schwingungsdauer von 10 Schwingungen Zieh dazu die Feder um ca. 7 cm nach unten und las sie los. Beginne bei der Zählung mit 0. Dividiere durch 10 10. Schwingungen

Versuch 2: Wir versetzen diese Anordnung in Schwingung und messen die Zeitdauer für 10 Schwingungen: 10·T =. . . s Schwingungsdauer T =. . . s Vergleiche dieses Ergebnis mit der Formel 10. Schwingungen

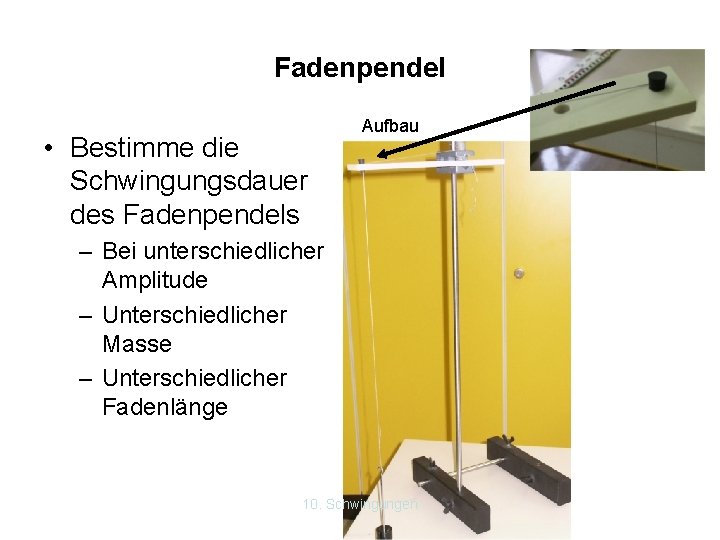
Fadenpendel • Bestimme die Schwingungsdauer des Fadenpendels Aufbau – Bei unterschiedlicher Amplitude – Unterschiedlicher Masse – Unterschiedlicher Fadenlänge 10. Schwingungen

Schwingungsdauer beim Fadenpendel: Fertige eine Skizze an! Versuch 1: Pendellänge l = 0, 6 m; Auslenkung ca. 5 cm; 2 Schlitzgewichte (2· 50 g + 10 g) 10·T =. . . s Schwingungsdauer T =. . . s Versuch 2: wie Versuch 1 jedoch Auslenkung ca. 10 cm 10·T =. . . s Schwingungsdauer T =. . . s Erkenntnis: Die Schwingungsdauer ist von der Amplitude. . . Versuch 3: Pendellänge l = 0, 6 m ; 4 Schlitzgewichte (4· 50 g + 10 g) (Beachte den Schwerpunkt !!) 10·T =. . . s Schwingungsdauer T =. . . s Erkenntnis: Die Schwingungsdauer ist von der Masse. . . 10. Schwingungen

Versuch 4: Pendellänge l = 0, 3 m 10·T =. . s Versuch 5: Pendellänge l = 1, 2 m 10·T =. . s Erkenntnis: Bei vierfacher Pendellänge ist die Schwingungsdauer. . . Vergleiche mit der Formel: Zusatz: Ermittle aus der Schwingungsdauer des Fadenpendels die Erdbeschleunigung! 10. Schwingungen

Harmonische Schwingungen sind Schwingungen, deren Weg. Zeit-Diagramm eine Sinus- oder Kosinusfunktion darstellen. Bei ihnen gibt es keinen Zusammenhang zwischen Amplitude und Schwingungsdauer. Beispiele: Federpendel, Fadenpendel, Stimmgabel, Blattfeder, . . . nicht: schwingende Saite. 10. Schwingungen

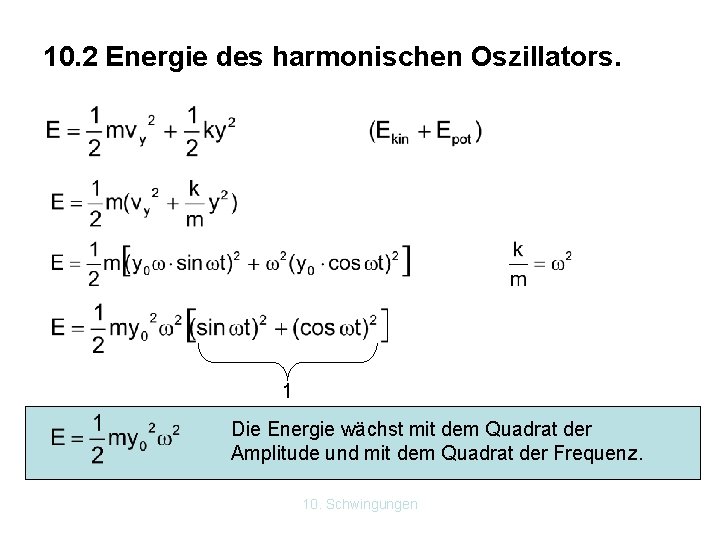
10. 2 Energie des harmonischen Oszillators. 1 Die Energie wächst mit dem Quadrat der Amplitude und mit dem Quadrat der Frequenz. 10. Schwingungen

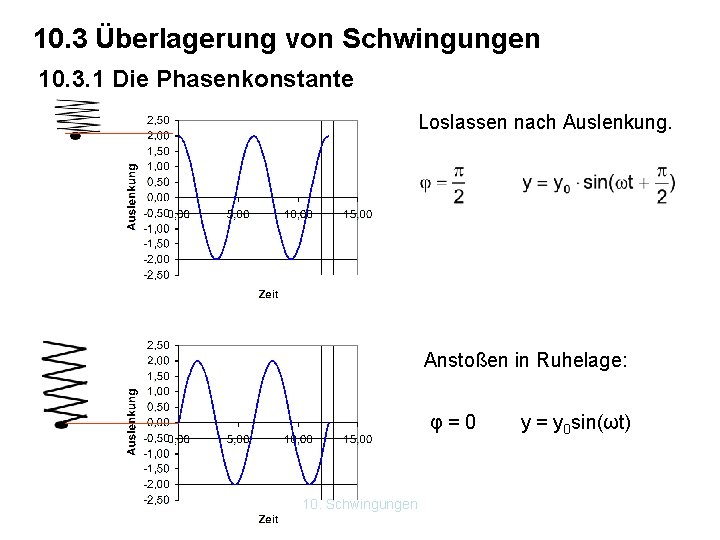
10. 3 Überlagerung von Schwingungen 10. 3. 1 Die Phasenkonstante Loslassen nach Auslenkung. Anstoßen in Ruhelage: φ=0 10. Schwingungen y = y 0 sin(ωt)

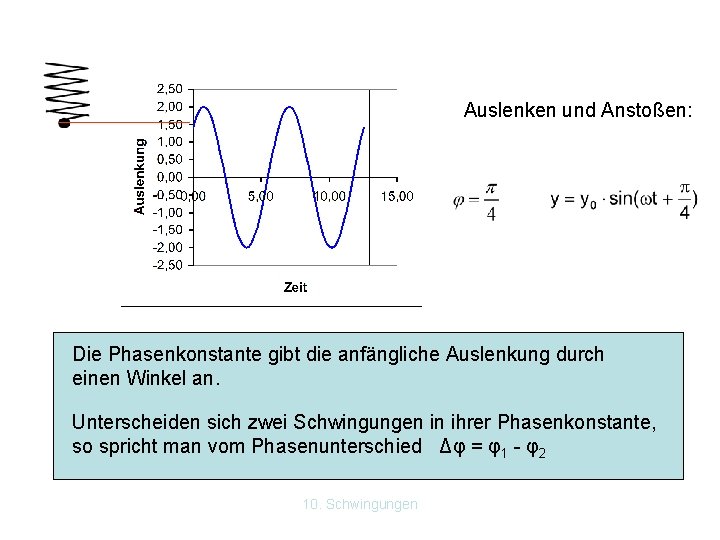
Auslenken und Anstoßen: Die Phasenkonstante gibt die anfängliche Auslenkung durch einen Winkel an. Unterscheiden sich zwei Schwingungen in ihrer Phasenkonstante, so spricht man vom Phasenunterschied Δφ = φ1 - φ2 10. Schwingungen

10. 3. 2 Addition von Schwingungen 10. 3. 2. 1 Addition kollinearer Schwingungen gleicher Frequenz Versuch: Zwei gleiche Stimmgabeln werden angestoßen. Mit Mikrophon und Oszillograph veranschaulichen. Ergebnis: Manchmal wird der Ton lauter, manchmal leiser. Mathematische Beschreibung: 1. Schwingung: 2. Schwingung: y 1 = y 01 sin(ωt) y 2 = y 02 sin(ωt + φ) 10. Schwingungen φ. . . Phasenverschiebung

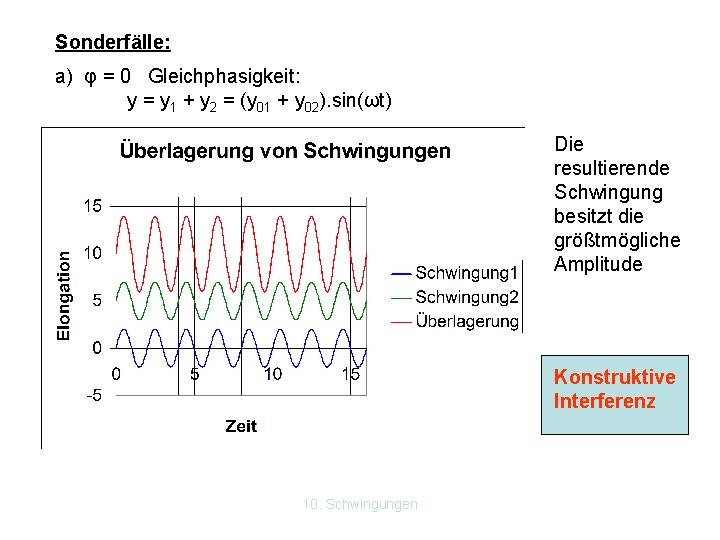
Sonderfälle: a) φ = 0 Gleichphasigkeit: y = y 1 + y 2 = (y 01 + y 02). sin(ωt) Die resultierende Schwingung besitzt die größtmögliche Amplitude Konstruktive Interferenz 10. Schwingungen

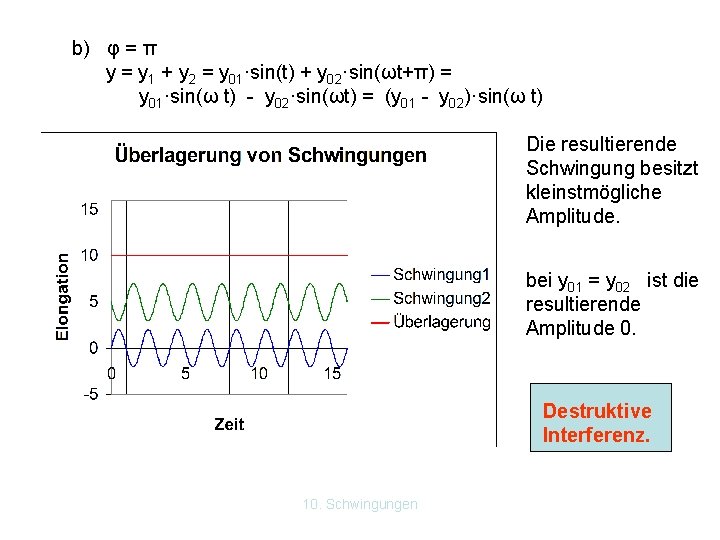
b) φ = π y = y 1 + y 2 = y 01·sin(t) + y 02·sin(ωt+π) = y 01·sin(ω t) - y 02·sin(ωt) = (y 01 - y 02)·sin(ω t) Die resultierende Schwingung besitzt kleinstmögliche Amplitude. bei y 01 = y 02 ist die resultierende Amplitude 0. Destruktive Interferenz. 10. Schwingungen

Die Überlagerung zweier harmonischer Schwingungen gleicher Frequenz und gleicher Schwingungsrichtung ergibt stets wieder eine harmonische Schwingung, deren Amplitude von den Amplituden der Einzelschwingungen und von ihrer Phasendifferenz abhängt. 10. Schwingungen

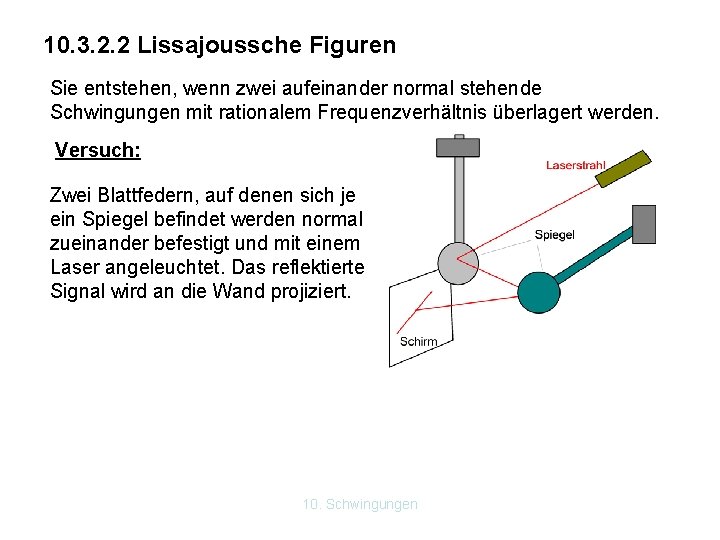
10. 3. 2. 2 Lissajoussche Figuren Sie entstehen, wenn zwei aufeinander normal stehende Schwingungen mit rationalem Frequenzverhältnis überlagert werden. Versuch: Zwei Blattfedern, auf denen sich je ein Spiegel befindet werden normal zueinander befestigt und mit einem Laser angeleuchtet. Das reflektierte Signal wird an die Wand projiziert. 10. Schwingungen

Mathematische Beschreibung: x - Schwingung: x = x 0 sin(ω1 t) y - Schwingung: y = y 0 sin(ω2 t+φ) φ. . . Phasenverschiebung Sonderfälle: 1. ω1 = ω2 = ω ; x 0 ; y 0 ; φ=0 Gerade 2. ω1 = ω2 = ω ; x 0 = y 0 ; φ = π/2 x - Schwingung: x = r. sin(ωt) y - Schwingung: y = r. sin(ωt + π/2) = r. cos(ωt) → Kreis x 0 ≠ y 0 → Ellipse 10. Schwingungen

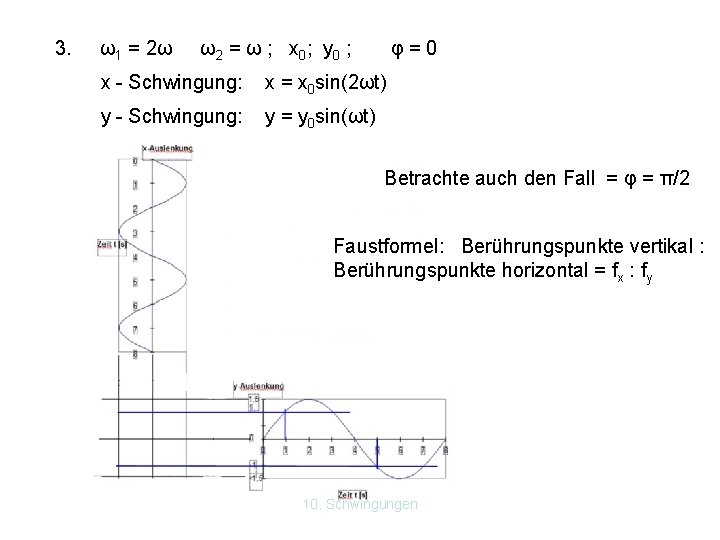
3. ω1 = 2ω ω2 = ω ; x 0 ; y 0 ; φ=0 x - Schwingung: x = x 0 sin(2ωt) y - Schwingung: y = y 0 sin(ωt) Betrachte auch den Fall = φ = π/2 Faustformel: Berührungspunkte vertikal : Berührungspunkte horizontal = fx : fy 10. Schwingungen

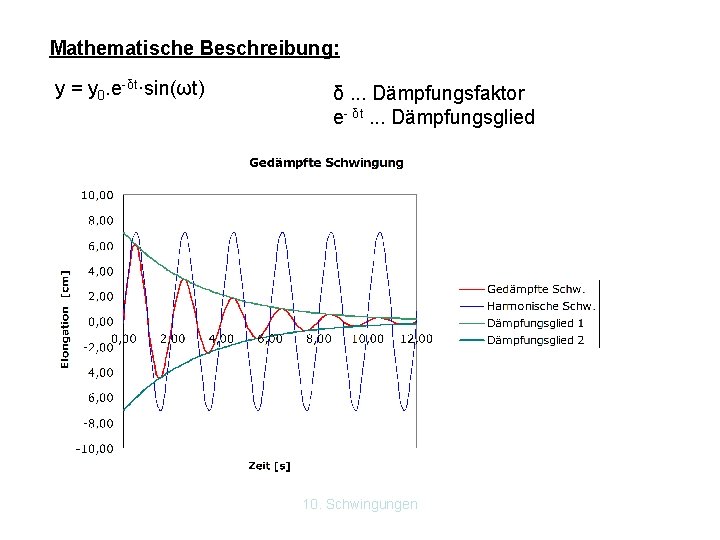
10. 4 Gedämpfte Schwingung Eine harmonische Schwingung hat eine konstante Amplitude und sollte unaufhörlich sein. Reale Schwingungen verhalten sich nicht so. Versuch: Pendel wird in Schwingung versetzt. Das Weg-Zeit Diagramm wird mit dem Computer aufgezeichnet. Die Amplitude der gedämpften Schwingung nimmt mit der Zeit ab. Die Schwingungsdauer der gedämpften Schwingung ist etwas größer als bei der ungedämpften Schwingung. Vgl. B. 6 RG S. 76 10. Schwingungen

Mathematische Beschreibung: y = y 0. e-δt·sin(ωt) δ. . . Dämpfungsfaktor e- δt. . . Dämpfungsglied 10. Schwingungen

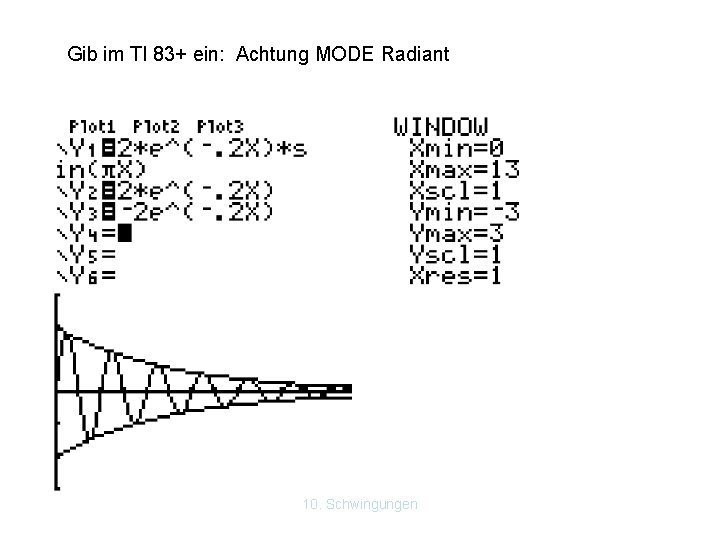
Gib im TI 83+ ein: Achtung MODE Radiant 10. Schwingungen

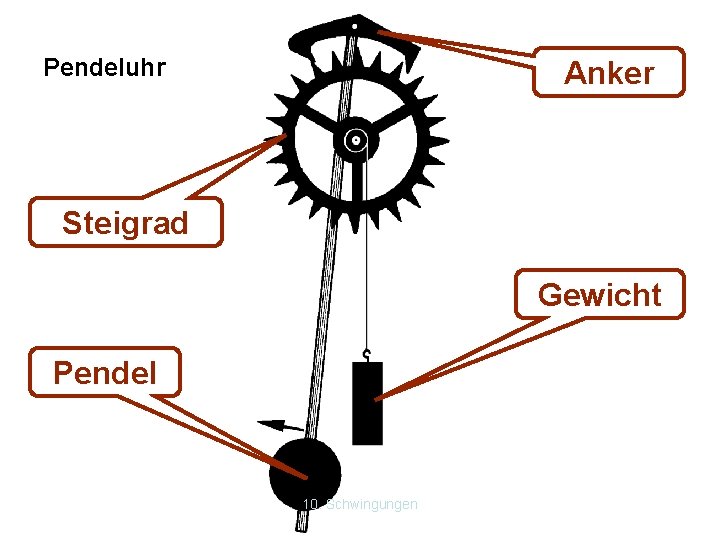
Um die Dämpfung zu vermeiden z. B. bei Uhren verwendet man Rückkopplungseinrichtungen. Sie führen die in Reibung umgewandelte Energie wieder zu, dass die Amplitude konstant bleibt. Beispiel: Pendeluhr 10. Schwingungen

Pendeluhr Anker Steigrad Gewicht Pendel 10. Schwingungen

Dämpfung kann aber auch erwünscht sein: Zeiger eines Analogmessgeräts, Stoßdämpfer. 10. Schwingungen

10. 5 Erzwungene Schwingung - Resonanz Schülerversuch: Die Spule mit 800 Windungen wird an den Funktionsgenerator angeschlossen. Einstellung: Frequenzbereich 1 Hz, Sinus Erhöhe mit dem Frequenzdrehknopf (links) die Frequenz sehr sorgfältig und beobachte was passiert. Miss die Auslenkungen der Blattfeder und trage sie in Abhängigkeit von der Frequenz auf. Beachte: Interessante Ereignisse müssen sich nicht mit "ganzzahligen" Frequenzen decken. 10. Schwingungen

Frequenz [Hz] Auslenkung in [mm] Trage die Werte in einem Diagramm auf. 10. Schwingungen

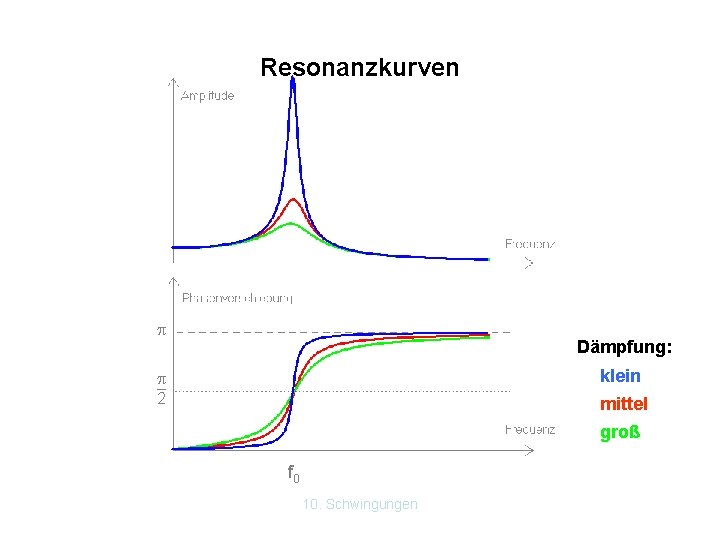
Resonanzkurven Dämpfung: klein – 2 mittel groß f 0 10. Schwingungen

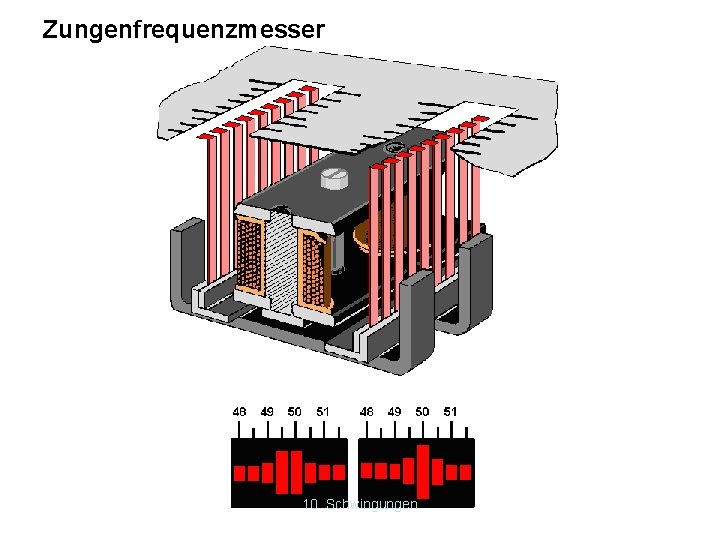
Die Amplitude der Blattfeder hängt von der Frequenz des Erregers ab. Ist die Frequenz des Erregers gleich der Eigenfrequenz der Blattfeder spricht man von Resonanz. Vgl. Abb. 77. 3 (BW 6 RG) Die Resonanzkurve ist um so höher, je geringer die Dämpfung ist. Im schlimmsten Fall (ungedämpft) → Resonanzkatastrophe. Lies Beispiele Buch Basiswissen 6 RG Seite 78. Tacoma Narrows Bridge Gebäudeschwingungen, Rotierende Maschinenteile, Resonanz von Tragflügeln, Resonanzkörper, Zungenfrequenzmesser 10. Schwingungen

Tacoma Narrows Bridge 7. November 1940 10. Schwingungen heute

Zungenfrequenzmesser 10. Schwingungen